N维势箱函数量子特性的可视化研究
郑兴荣,郑燕飞
(1. 陇东学院 电气工程学院 物理系,甘肃 庆阳 745000;2. 西南大学 物理科学与技术学院,重庆 400715)
量子理论是现代物理学两大支柱之一,不仅是自然科学的基础理论,也是整个现代科学技术的基础理论,应用于各个领域[1],尤其是量子通信、量子计算和量子精密测量. 而势箱函数作为量子理论的最简单、最重要模型之一,在理论研究和实践中非常重要,是学习量子理论的基础和入门[2]. 对于势箱函数模型,根据粒子体系的条件,得到粒子的势能函数,进而得到粒子的运动符合薛定谔方程;结合归一性,通过理论推导,我们可以得到势箱函数的波函数和能级表达式,从而得到波函数、能级及其概率密度的分布特点,了解粒子体系的特性[3,4]. 因此,学习势箱函数及其相关特性对于今后量子理论的其他模型学习提供了借鉴. 另外,势箱函数的应用范围非常广泛,如金属内自由电子的运动、共轭分子内电子的运动、真空管中电子的运动、原子内部电子在两个能级之间的跃迁、零点能等[5-8]. 通过对势箱函数的研究,可以有效的说明量子理论处理微观体系的优势,在处理过程中获得的信息可帮助了解原子、分子内的电子等各种粒子的运动.
N维势箱函数及其特性的研究,在理论和应用上都非常重要. 近几年,随着 MATLAB软件的发展,运用理论推导或者仿真模拟来研究势箱函数及其特性取得了一些结果[7-10],尤其是一维势箱函数的研究. 虽然国内外众多团队对势箱函数及其特性的研究较多,但二维及以上势箱函数的特性更加复杂,在研究过程中存在理论方法描述困难、计算繁琐和运行时间过长等一些客观因素,因此二维及以上势箱函数的研究很少,尤其是三维势箱函数的研究存在很大空白. 另外,虽然一维到N维势箱函数的波函数及其概率密度可由薛定谔方程给出低能级上的解析解,但其推导和结论的理解对初学者而言是个难点. 基于此,本文运用MATLAB软件的数值计算和仿真功能,通过可视化研究,解决了势箱函数在教学和科学研究方面的难题,尤其对于抽象性概念的理解具有重要意义,如简并度、概率密度等. 同时,也为用MATLAB数值计算和仿真解决其他问题提供了案例. 因此,本文的研究思路和方法有一定的参考价值和借鉴作用,尤其是首次运用MATLAB软件得到了较为抽象的四维图形.
1 理论模型与推导
1.1 一维势箱函数及其特性
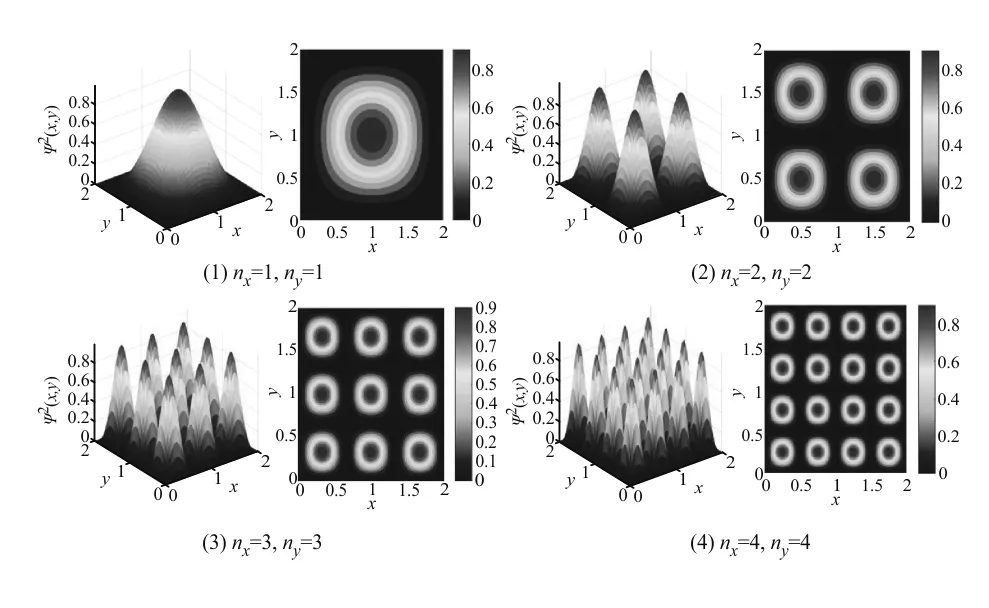
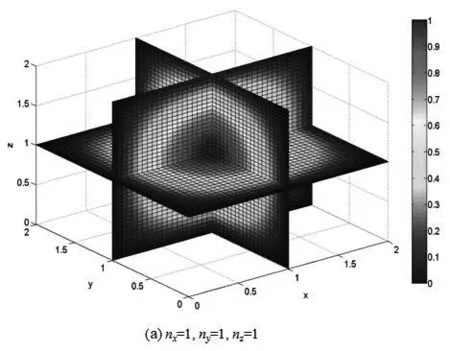
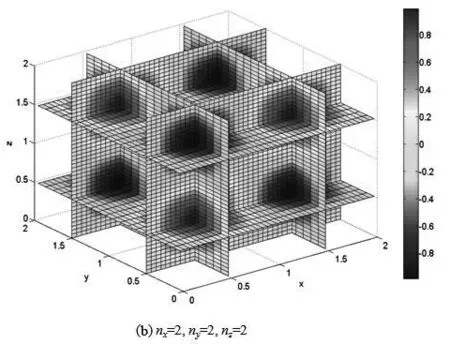
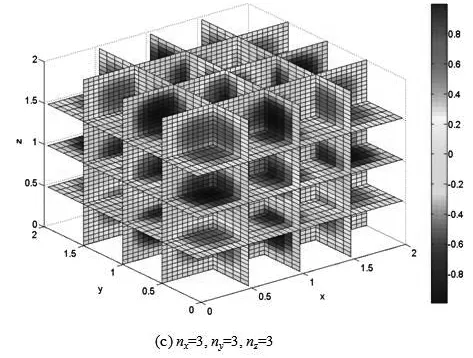
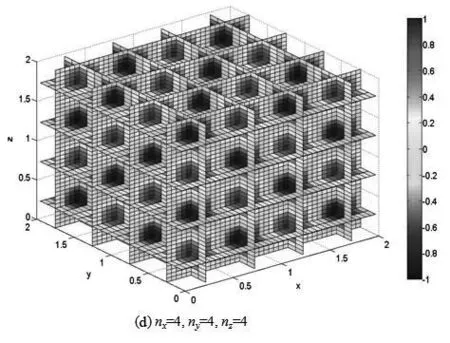
在一维空间里,质量为μ的粒子在区间0 (1) 满足上式条件的势就称为一维无限深势阱,也就是一维势箱模型. 一维势箱模型是一个抽象模型,可用来描述微观体系的基本运动,如平动. 其模型及其对应的势箱函数示意图,如图1所示. 模型图 函数示意图图1 一维势箱函数示意图及其模型 对于一维势箱,阱内(0 (2) 通过一系列简化及求解,并利用归一化条件,得到一维势箱中粒子的定态波函数为 (3) 对应的体系能量为 (4) 式中n表示的是量子数,n=1,2,3,….当n=1时,对应的E1是粒子的基态,当n>1时对应的是粒子的激发态. 同时,粒子在箱外出现的概率为零,则在箱内各处出现的概率的总和满足归一化条件: (5) 二维势箱中,粒子在其中的运动满足薛定谔方程,其表述为 (6) 通过分离变量法求解,得到了二维势箱波函数及其能级,分别为: (7) (8) 三维势箱中,粒子满足的的薛定谔方程为 (9) 利用分离变量法,得到了三维势箱波函数及其能级,分别为: (10) (11) 根据一维势箱函数波函数的理论公式,运用MATLAB软件进行数值计算与仿真,绘制了不同能级下一维势箱函数的波函数图像,得到了势箱函数的8个本征波函数图和8个对应的概率密度图,如图2所示. 图2 不同能级下一维势箱函数的波函数和概率密度 另外,根据能级公式,我们也得到了长度为a的一维势箱函数的能级图,如图3所示. 图3 一维势箱函数的能级图 从图2和图3我们可以看到:一维势箱中粒子的能量是量子化的、不连续的;量子数n不能为零,且n越大对应的能级越高,质量m越大,对应的能级越低;在一定的条件下,a越大(粒子运动范围越大),对应的能级越低;节点数为n-1,节点越多,波长越短,频率越高,能级越高. 另外,图形显示这种可视化的结果与理论结果完全符合. 根据式(7),取a=b=2,运用MATLAB软件得到了9种情况下二维势箱函数的波函数及其等值线图,如图4所示. 图4 不同的nx、ny对应的二维势箱函数的波函数及其等值线分布 另外,结合图4,利用波函数的理论公式,还得到二维势箱函数的概率密度图及其伪真彩图,如图5所示. 图5 不同的nx、ny值对应的波函数概率密度及其伪真彩图 通过可视化的仿真图,我们可以得到:二维势箱函数的峰值的个数为nx×ny,且波函数与Ψ=0平面的交线数也为nx×ny;而且二维势箱函数的概率密度分布的极大值个数也为nx×ny. 一般情况下,普通的二维势箱模型下的微观粒子的简并度是不确定的. 但对于二维正方势箱函数模型,其箱内微观粒子的能级简并度分为2种情况:1) 一般情况:nx=ny时,粒子无简并;nx≠ny时,粒子二度简并; 2) 特殊情况:粒子可能是更高度简并,如nx=10、5,11、2,对应的ny=5、10,2、11时,粒子的简并度是四. 图示结果和理论结果完全吻合. 根据式(10),取a=b=c=2,运用MATLAB软件得到了4种情况下三维势箱函数的波函数图,如图6所示的是三维势箱函数的四维空间切片图. 根据以上理论和图形,发现三维势箱函数的公式能够反映出波函数的相关特性,且三维势箱函数粒子的量子数分别为nx、ny、nz,则简并度为nx+ny+nz. 同时,借助MATLAB软件的色彩实现了四维图示表现,得到了4种情况下的三维势箱函数的四维空间切片图. 图6 不同nx、ny、nz值对应的三维势箱函数四维空间切片图 势箱函数作为量子理论的最简单、最重要模型之一,在实际生活中非常重要,是学习量子理论的基础和入门. 本文通过量子理论系统、全面地研究了量子力学中N维势箱函数的波函数、能级和概率密度. 最后,运用MATLAB软件对势箱函数的所有特性进行了仿真模拟,进行了可视化研究. 结果表明:一维到N维势箱中,粒子的能量是量子化的、不连续的;量子数n不能为零,且n越大对应的能级越高,质量m越大,对应的能级越低. 一般情况下,一维势箱函数的长度a越长(粒子运动范围越大),对应的能级越低;节点数为n-1,节点越多,波长越短,频率越高,能级越高. 二维势箱函数峰值的个数为nx×ny,且波函数与Ψ=0平面的交线数也为nx×ny;概率密度分布的极大值个数也为nx×ny. 对于简并度,一般情况下,普通的二维势箱模型下的微观粒子的简并度是不确定的. 但对于二维正方势箱函数模型,其箱内微观粒子的能级简并度分为2种情况:1)一般情况:nx=ny时,粒子无简并;nx≠ny时,粒子二度简并; 2)特殊情况:粒子可能是更高度简并,如nx=10、5,11、2,对应的ny=5、10,2、11时,粒子四度简并. 三维势箱函数粒子的能量量子数分别为nx、ny、nz,简并度为nx+ny+nz. 最后,借助MATLAB软件的色彩实现了四维表现,得到了4种情况下的三维势箱函数的四维空间切片图. 本文的这种可视化研究,从理论方法之外解决了势箱函数在教学和科学研究的难题,尤其对于抽象性概念的理解具有重要意义,如能级的量子化、简并度、概率密度等概念和公式. 同时,也为用MATLAB数值仿真解决其他问题提供了案例. 因此,本文的研究思路和方法有一定的价值和借鉴作用,尤其是首次运用MATLAB软件得到了较为抽象的四维图形.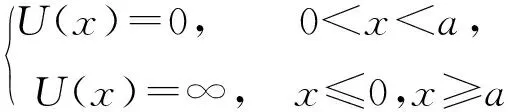
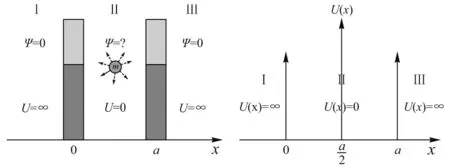
1.2 二维势箱函数及其特性
1.3 量子力学中的三维势箱函数
2 仿真结果与讨论
2.1 一维势箱函数的MATLAB数值仿真
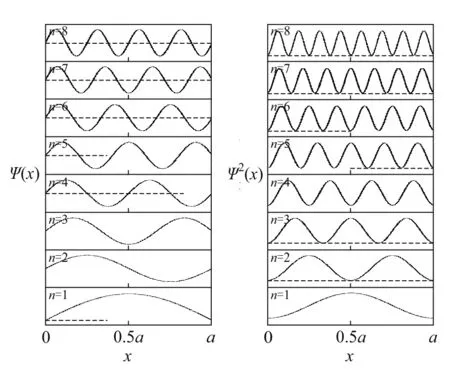

2.2 二维势箱函数的MATLAB 数值仿真

2.3 三维势箱函数的MATLAB数值仿真
3 结论

