TC4钛合金铣削性能分析及多目标参数优化

鲍 骏，白海清，2*，任 礼，安熠蔚，秦 望

(1.陕西理工大学机械工程学院，汉中 723001；2.陕西省工业自动化重点实验室，汉中 723001)

钛合金材料具有强度大，耐高温耐腐蚀以及密度小等一系列优良特点，被广泛应用于航天航空及船舶等领域[1]。在钛合金的加工中,铣削加工是极为普遍的一种方法。但是,由于钛合金的低导热性和低弹性模量,将增加切削中的切削力和切削热,导致切削温度的进一步升高,继而加剧刀具的磨损[2]。同时在铣削加工中，铣削参数的选择不当会导致刀具的磨损程度加大，零件变形等诸多不利现象，严重影响了加工的效率，增大了制造的成本[3]。钛合金作为典型的难加工材料，对加工参数的要求更为严苛[4]。因此针对钛合金铣削特性的相关分析以及如何对铣削参数进行合理的选取这一方面的研究十分必要。

针对钛合金铣削加工的研究中，王晓明等[5]、孙鹏程等[6]采用了正交试验法分别研究了铣削参数对工件表面粗糙度、铣削力的影响规律。Pratap等[7]考虑刃口半径、切片厚度和切削用量等因素，采用有限元仿真方法，建立了微端铣削TC4钛合金的铣削力模型。Hao等[8]研究了球头铣刀加工TC4钛合金过程中轴向切削深度、铣削方式和加工倾角对铣削力的影响。然而只从铣削力或表面粗糙度等单一方面入手进行分析，所得的结论往往不够具体，实际加工中应考虑多个方面的条件要求。在多方面综合考虑的基础上，如何对工艺参数进行合理的选取，相关学者们通过计算机算法来寻求相对最优解。陈建岭等[9]以高加工效率与低刀具磨损度作为优化目标，建立了多目标优化模型并采用ENSGA-Ⅱ算法进行了优化计算。杨帆等[10]将高加工效率，高表面质量，低加工成本三方面要求引入优化模型，通过NSGA-Ⅱ算法得到了最优解集，并通过仿真试验进行了验证。在铣削方面，关于采用算法进行的多目标参数优化的研究中，当优化目标为2个时，通过算法得到的单个最优解集可为参数选取的决策提供参考依据。而当优化目标为3个时，处理方法大多为将优化目标两两组合进行求解，这无疑增大了求解的次数，且在考虑两两目标组合求解时忽略了第3个目标，同时所得多个解集也对决策者进行决策造成了一定的困难，加大了参数选取的工作量。

通过正交铣削试验，分析了TC4钛合金的铣削力、表面粗糙度、材料去除率受铣削参数即背吃刀量、侧吃刀量、主轴转速与进给速度的影响程度。并以铣削力，表面粗糙度，材料去除率为优化目标建立了优化模型，在遗传算法的基础上，同时将3个优化目标引入，一次性直接进行求解后得到了最优解集，为参数的选取提供了参考依据。相比两两目标组合求解的处理方法，减少了求解的次数，同时也简化了可提供参考决策的解集个数。通过试验验证了该算法的可行性。

1 铣削试验

1.1 试验目的与试验路线

本试验旨在寻求钛合金的铣削加工的优质铣削参数组合，评判指标包括铣削力F、表面粗糙度Ra和材料去除率Q，其中材料去除率的表达式为

(1)

式(1)中：Q为材料去除率，cm3/min；ap为背吃刀量，mm；ae为侧吃刀量，mm；vf为进给速度，mm/min。

所使用方法为正交试验法与计算机智能算法相结合，试验路线为：①通过正交试验法得到初步数据,对其进行极差分析,研究铣削参数即背吃刀量ap、侧吃刀量ae、主轴转速n与进给速度vf对各个评价指标的影响趋势与规律；②基于极差分析结果,建立多目标优化模型,通过遗传算法进行求解；③得到优质解集并再次通过实际铣削试验进行验证。

1.2 试验材料与设备

试验材料为100 mm(长)×100 mm(宽)×10 mm(高)的TC4钛合金金属板，铣削试验设备选用数控立式铣床，型号为汉川机床公司生产的XK950型。刀具选用整体式硬质合金立铣刀，所属系列为DG-ATD03，由上海工具厂生产，参数如表1所示。使用瑞士Kistler公司生产的9257B型测力仪(包括三向动态压电式测力仪、电荷放大器及数据转换采集器等部件组成)对铣削试验过程中的铣削力进行测量，铣削力测量系统如图1所示。使用基恩士VHX-7000超景深显微镜，镜头Z250∶X300。测量工件铣削后的表面粗糙度，表面粗糙度结果采用五点测量法选取平均值进行分析以提高试验普遍性和可靠性。

表1 铣刀参数Table 1 Milling cutter parameters

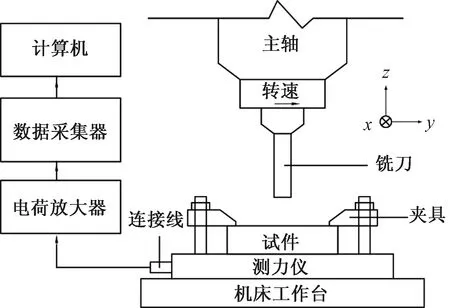
图1 铣削力测量系统Fig.1 Milling force measurement system

2 试验方案与结果分析

采用四因素三水平正交试验方案，因素水平如表2所示。铣削力，表面粗糙度与材料去除率结果如表3所示。零件表面形貌如表4所示。

表2 试验因素水平Table 2 Experimental factors level

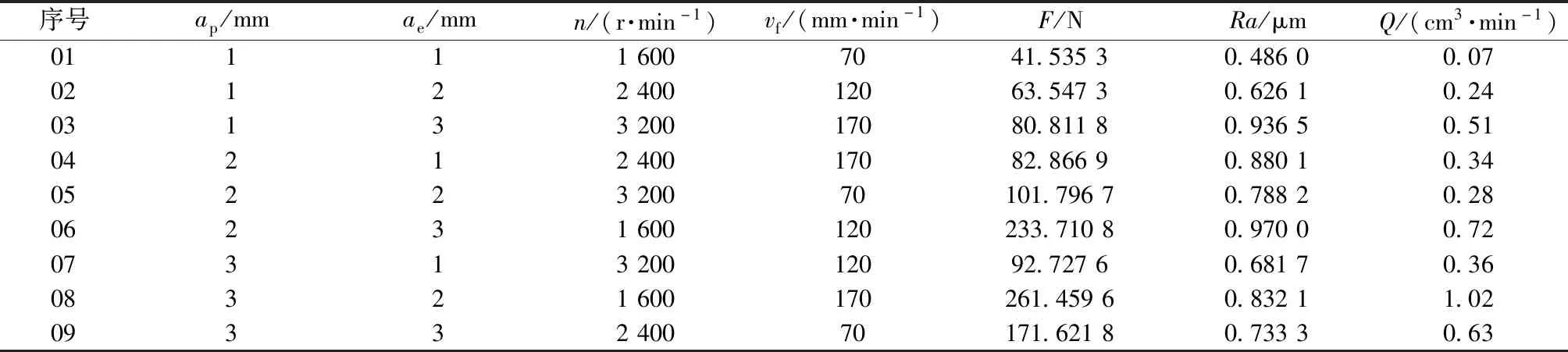
表3 铣削力与表面粗糙度测量结果Table 3 Measurement results of millingforce and surface roughness

表4 表面形貌图Table 4 Pictures of surface topography

续表4

采用极差分析法，对试验得到的结果进行分析。定义各水平所在试验组结果为KXY，极差为RY，通过计算各因素的极差值并对其进行比较分析可以得到各因素不同水平对实验结果的影响，其计算公式为

(2)

(3)

2.1 铣削力分析

通过式(1)、式(2)计算得到铣削力极差分析结果如表5所示。设定正交分析为望小分析[11],铣削力越小,切削时的振动与切削热越小，对零件表面质量有利。由表5可得，其因素对结果的影响次序为:

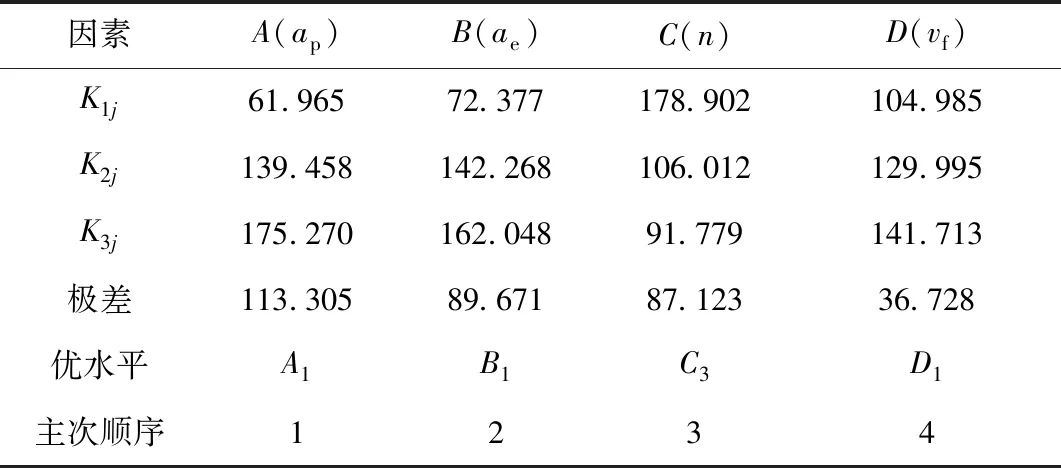
表5 铣削力极差分析Table 5 Analysis of milling force range

ap>ae>n>vf。可得优质参数组合为A1B1C3D1根据表5数据结果，绘制各因素与铣削力的关系图如图2所示。

图2 铣削力变化趋势图Fig.2 Variation trend of milling forces

由图2(a)可得，随着背吃刀量的增加，铣削力整体呈上升趋势。原因在于：背吃刀量的增加，使得切削层横截面增大，去除材料所需要的能量增大。由于钛及钛合金在高温时化学活性很高,铣削力[1 mm,2 mm]区间涨幅均大于[2 mm,3 mm]区间，推测是在切削热的影响下，与空气中的氢(水汽)、氧与氮等元素产生化学反应从而生成表面脆硬层，表面脆硬层的硬度要高于钛合金内部硬度[2]，适当增大背吃刀量可以使刀尖在一定程度上避开表面硬化层,直接切除材料；由图2(b)可得，侧吃刀量的增加可使得刀具和工件的接触面积增大，单位时间内切削量与摩擦力增大，故侧吃刀量增大铣削力上升。铣削力在[1 mm,2 mm]区间涨幅大于[2 mm,3 mm]区间，这是因为摩擦力增大一定程度上导致铣削温度上升，钛合金出现了高温软化现象，所去除材料需要的能量减少；由图2(c)可得随着主轴转速的增大，铣削力整体呈下降趋势。这是因为随着主轴转速的增加，铣削速度上升，单位时间内产生的切屑增加，一定程度上会导致铣削力的上升。但由于钛合金材料本身较强的黏附性，切屑无法迅速排除，其中部分碎屑会黏附在刀具上，使得摩擦力增大导致切削区域温度迅速上升，钛合金高温软化现象明显，这时去除材料所需要的能量减少，故其铣削力不升反降。但铣削力的上升速率与材料的高温软化速率并不相等，随着转速的继续增加，刀具单位时间内切入切出量增大，铣削力上升速率增加，软化现象的影响相对减弱，在二者的共同影响作用下，会出现铣削力在[2 400 r/min,3 200 r/min]区间相对于[1 600 r/min,2 400 r/min]区间下降幅度明显减缓这一现象；由图2(d)可得，随着进给速度的增大，铣削力呈上升趋势，这是因为随着进给速度的增大，单位时间内材料去除率增大，刀具切除材料所做的功增大，在进给速度为[120 mm/min,170 mm/min]区间内铣削力涨幅大于[70 mm/min,120 mm/min]区间，这是因为随着进给速度的增大，水平加工面内刀具切削过程中第一变形区(剪切滑移)面积增大，TC型钛合金材料本身受剪切变形的影响大于压缩变形，切除材料所产生的切屑增加，黏附在刀具上的碎屑增加，导致摩擦力变大，切削区域温度上升，钛合金出现了高温软化现象。

2.2 表面粗糙度分析

同理计算可得表面粗糙度极差分析结果如表6所示。同设定分析为望小分析,表面粗糙度数值越低,零件表面质量越好。由表6可得，其因素对结果的影响次序为:vf>ae>ap>n。可得优质参数组合为D1B1A1C2。绘制各因素与表面粗糙度的关系图(图3)。

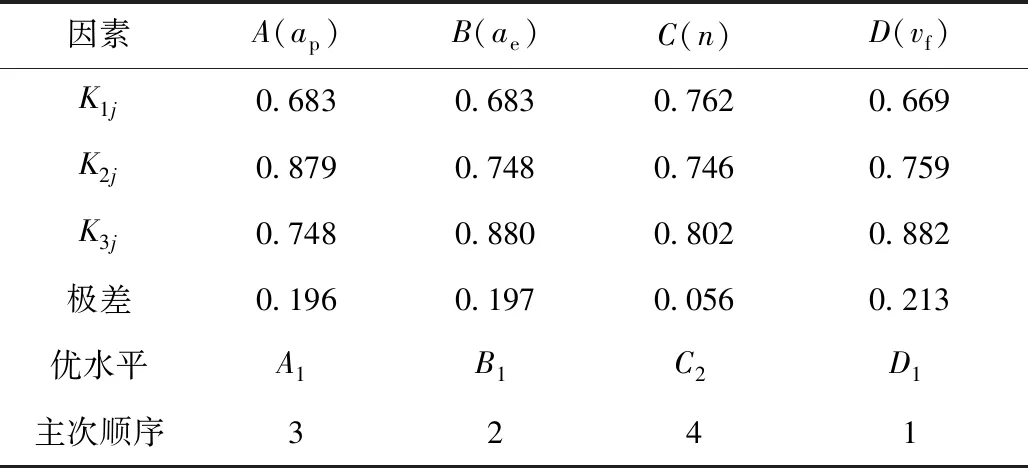
表6 表面粗糙度极差分析Table 6 Surface roughness range analysis

图3 表面粗糙度变化趋势图Fig.3 Surface roughness variation trend diagram

由图3(a)可得，背吃刀量在[1 mm,2 mm]区间时，表面粗糙度增大，这是因为随着背吃刀量的增大，切削层横截面积增大，材料的挤压量变形增大，故其表面粗糙度上升。钛合金在切削热的影响下，与空气中的元素产生化学反应生成表面脆硬层，适当的增大背吃刀量可一定程度上避开脆硬层，直接切削其内部材料，内部材料较脆硬层更易切除，故在背吃刀量为[2 mm,3 mm]区间内表面粗糙度下降。由图3(b)可得，随着侧吃刀量的增加，表面粗糙度一直增大，这是因为侧吃刀量的增大，单位时间内材料去除率增大，刀具磨损加重。由图3(c)可得随着主轴转速的增大，表面粗糙度先减小后增大，这是因为随着主轴转速的增大，钛合金材料出现了高温软化现象，材料较易切除，表面粗糙度减小，当主轴转速继续增大时，刀具会出现颤振现象，影响了加工的精度。故在[2 400 r/min,3 200 r/min]区间表面粗糙度会增大。由图3(d)可得，随着进给速度的增大，表面粗糙度一直增大。这是因为随着进给速度的增加，刀具在进给方向的移动速度增加，单位切削面积内刀具切削次数减小，故其表面粗糙度增加。

2.3 材料去除率分析

根据式(1)计算的材料去除率极差分析结果如表7所示。设定为望大分析，材料去除率越大其加工效率越高。虽然式(1)中并未出现主轴转速n，但根据极差分析数据显示，n的变化对材料去除率造成了一定影响，推测应为实际试验中各因素的交互影响。因本次分析中不考虑交互因素影响，故对主轴转速n只做数据分析，不做原因分析。

由表7可得，因素对材料去除率的影响次序为ap>ae>vf>n。可得优质参数组合为A3B3D3C1，根据表7做各因素与材料去除率的关系图(图4)。

表7 材料去除率极差分析Table 7 Material removal rate range analysis

由图4可得，背吃刀量、侧吃刀量的增加会导致单位时间内的切削面积增大，进给速度升高会导致单位时间内切削量的增加，以上原因都会导致刀具的磨损量增大，故其材料去除率上升，而随着主轴转速的增大，材料去除率减小，且在[2 400 r/min,3 200 r/min]区间内材料去除率减小速率降低。分析可知，铣削力、表面粗糙度、材料去除率受铣削参数的影响程度并不相等，正交分析法无法对多个判别指标同时进行选优。实际加工中，不能仅考虑单一指标故需建立优化模型,使用计算机智能算法对其进行求解。

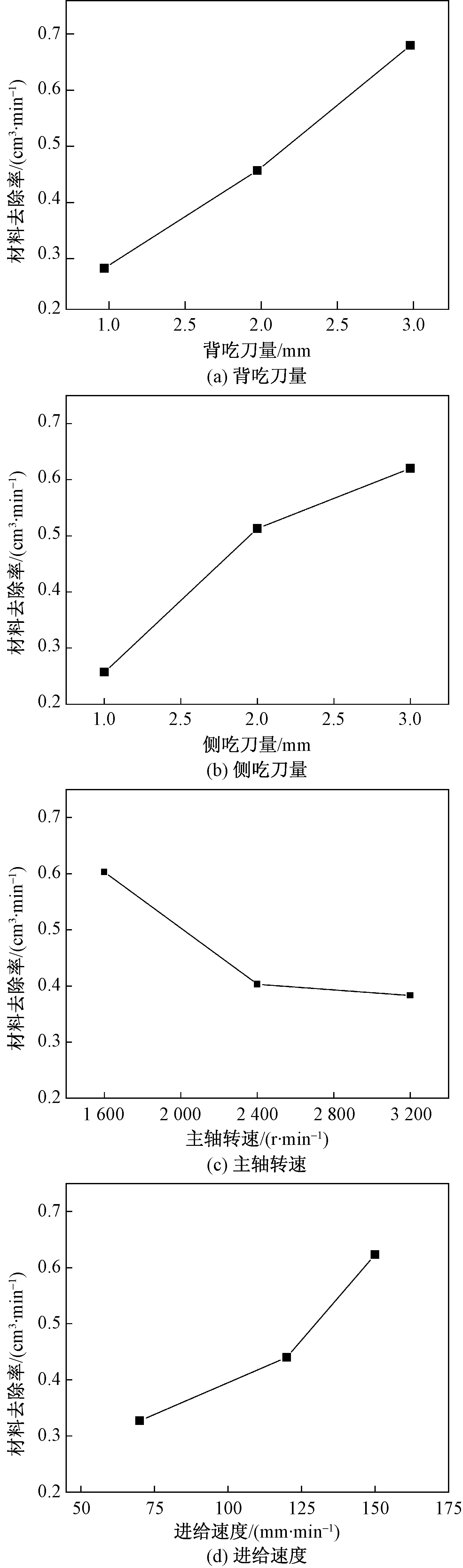
图4 材料去除率变化趋势图Fig.4 Material removal rate variation trend diagram

3 基于遗传算法的多目标优化

3.1 遗传算法原理

遗传算法是一种模拟生物界自然选择和自然遗传机制的随机搜索算法[12]。该算法将问题的求解模拟成生物进化过程，基于遗传学并遵循大自然的优胜劣汰原则，对群体进行反复复制、交叉和变异等操作，不断更新群体，以求解获得满足适应度函数要求的解，遗传算法流程图如图5所示。

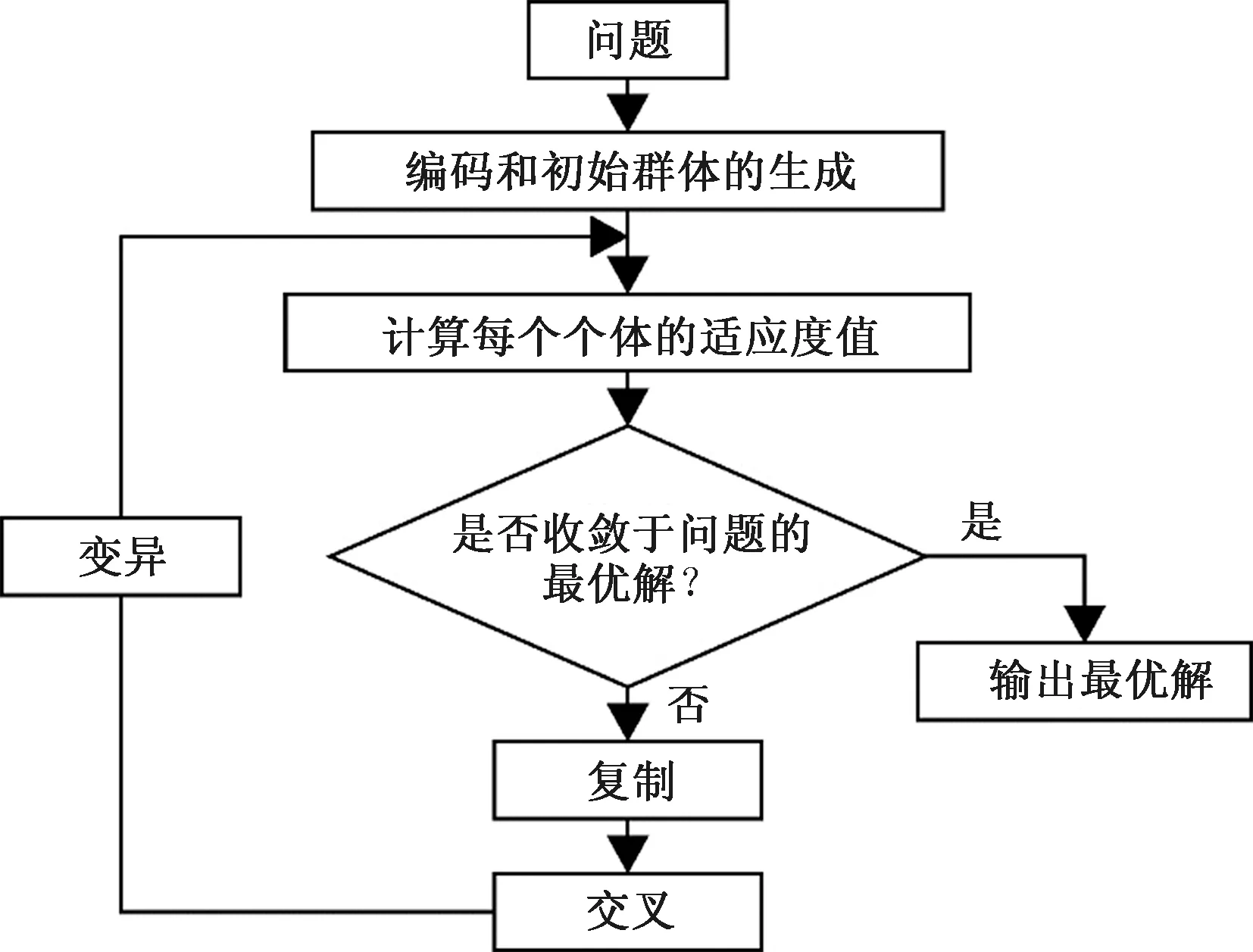
图5 遗传算法流程图Fig.5 Flow chart of genetic algorithm

3.2 多目标优化问题

实际中诸多工程应用问题中需要同时对多个目标进行优化，相互制约的,在使得一个优化目标性能改善的同时往往是以损失其他目标的性能为代价的，这类问题被称为多目标优化问题(multi-objective optimization problem,MOP)，并且不同于单目标优化问题，多目标优化问题的最优解是由一系列非劣解组成的最优解集[13]。以最小化问题为例，可将多目标优化问题定义为

(4)

式(4)中：x=[x1,x2,…,xn]∈Rn为n维决策变量；F(x)为n维目标函数；fi(x)为单个目标与自变量的关系式，遗传算法中称为适应度函数，i=1,2,…，m,m∈R+；gi(x)≤0为第i个不等式约束条件；p为不等式约束个数；hj(x)为第j个等式约束条件；q为等式约束条件个数。

3.3 适应度函数模型建立

由多目标优化问题可知，使用遗传算法对目标进行优化时，需要用到优化目标的适应度函数。可通过回归分析法对试验数据与结果进行分析，建立回归方程并使其作为适应度函数[14]。回归分法建模属经验建模，侧重于实验过程中产生的数据分析[15]。材料去除率函数关系式已知，可直接作为适应度函数。铣削力与表面粗糙度设定为望小分析,材料去除率越大,加工效率越高,故材料去除率设定为望大分析,评价指标包括材料去除率、铣削力与表面粗糙度。由于主轴转速与背吃刀量，侧吃刀量，进给速度所差数量级较大，为了保证回归方程的精确度以及遗传算法结果的可靠性，对铣削参数进行变换，可表示为

(5)

3.3.1 铣削力回归方程建立

铣削力回归模型采用指数拟合法，可表示为

(6)

式(6)中：K为影响系数；bi为待求系数，i=1,2,3,4。

对其两边求对数可得

lgF=lgK+b1lgx1+b2lgx2+b3lgx3+b4lgx4

(7)

令lgF=y,lgK=b0,lgxi=βi可得

y=b0+b1β1+b2β2+b3β3+b4β4

(8)

采用最小二乘回归法，得出所求系数bi，铣削力回归公式为

(9)

对式(9)采用F检验，所得F(4，4)=43.606 1，[F(m，n)中，m为参与回归的自变量个数，n=试验组总组数-自变量个数-1]，大于临界值F0.05(4，4)=6.388，回归方程可以使用。

3.3.2 表面粗糙度回归方程建立

表面粗糙度进行指数拟合时发现其回归方程效果不佳，故采用多项式拟合法进行逐步回归[16]，经拟合发现，一次多项式拟合方程回归程度不显著，三次多项式拟合结果严重失拟合，二次多项式结果最佳。本次试验自变量个数为4个，根据数学理论可得，其正交四元二次多项式为

(10)

式(10)中：a0、aj、aij、ajj共15个未知系数，实际试验数据只有9组，根据多元线性非齐次方程组求解原理，其所组成的增广矩阵并不满秩，无法求解。故需要舍弃不显著自变量因素。通过编写M文件并使用MATLAB求解后，回归方程的表达式为

(11)

使用最小二乘回归法得到表面粗糙度回归方程为

Ra=-0.179 4+0.992 0x1-0.042 7x3-

0.000 7x2x4+0.001 2x3x4

(12)

经检验，回归方程F(7，1)=11 309.7，远大于临界值F0.05(7，1)=236.8，表明回归方程可以使用。

3.4 优化模型的建立

3.4.1 目标函数

参与的目标优化的自变量x1、x2、x3、x4，矢量表达式为

U=(x1,x2,x3,x4)T

(13)

记铣削力回归方程F为y1(x)，表面粗糙度回归方程Ra为y2(x)，材料去除率方程Q为y3(x)，本次使用求解方法为最小值问题法，因而铣削力与表面粗糙度取值为miny1(x)、miny2(x)，材料去除率取值为-maxy3(x)。优化目标函数为

minf(x)=[y1(x),y2(x),-y3(x)]T

(14)

3.4.2 约束条件

对自变量取值范围进行约束。

(1)背吃刀量约束为

(15)

(2)侧吃刀量约束为

(16)

(3)主轴转速约束为

(17)

(4)进给速度约束为

(18)

故x1、x2、x3、x4取值范围为

gi(x)=[g1(x),g2(x),g3(x),g4(x)]T

(19)

综上所述，TC4钛合金铣削参数的多目标优化模型为

(20)

3.4.3 优化模型的求解

(1)根据铣削工艺参数确定TC4钛合金铣削参数的取值范围为

(21)

(2)基于遗传算法，利用MATLAB软件编写M文件进行求解，[y1(x),y2(x),y3(x)]是由3个目标适应度值组成三维散点图，将其目标适应度值全部引入，初始生产200个样本，前端显示系数设为0.2，最后求解所得40个样本，即解集。Pareto前端解集如图6所示。

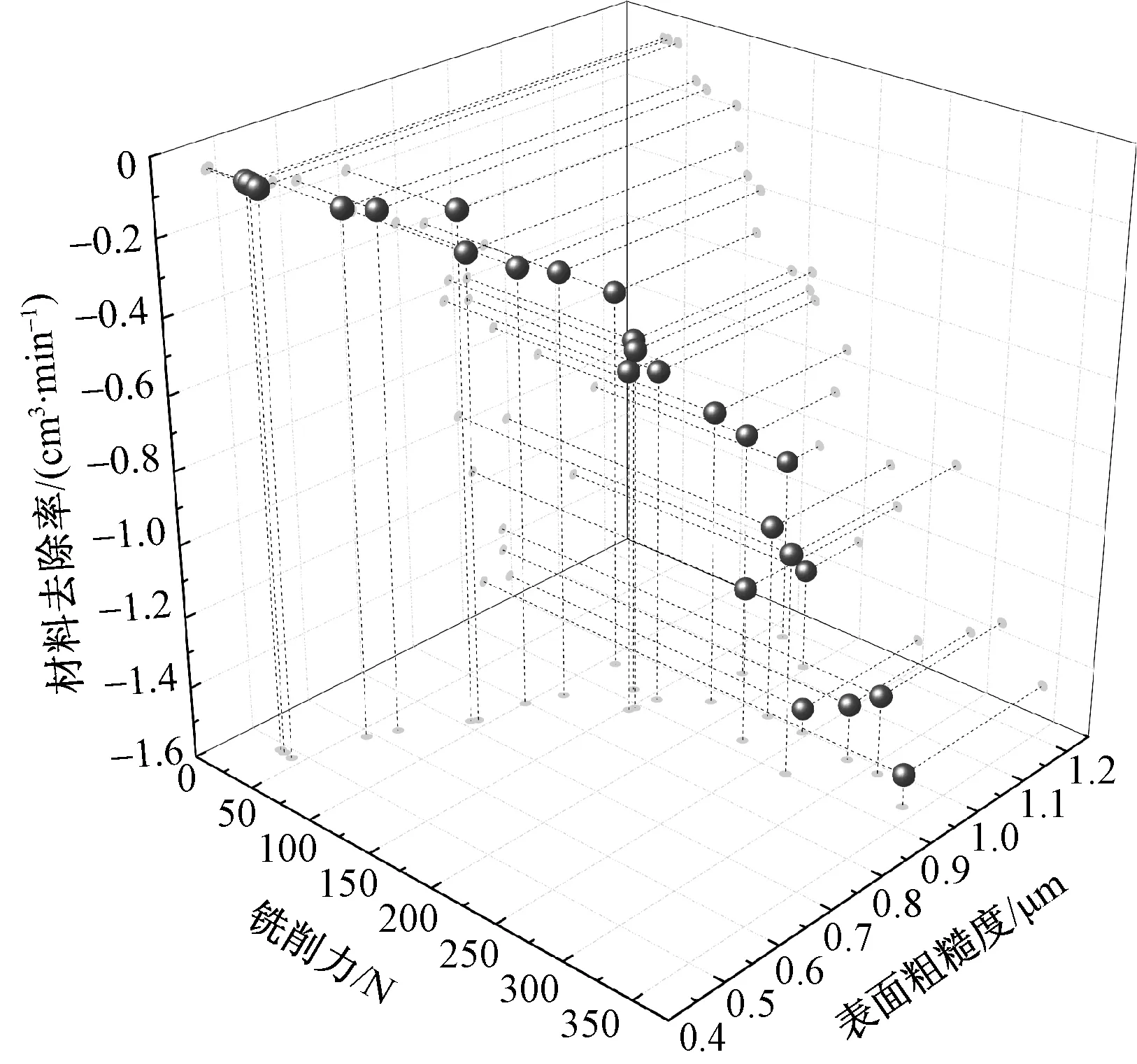
图6 遗传算法Pareto前端Fig.6 Genetic algorithm Pareto front end

4 优化结果验证

经遗传算法优化求解后，在解集中挑选3组参数组代入回归方程进行计算，预测结果如表8所示。同时再次进行铣削试验对其进行验证,并将所得结果与预测值进行对比,结果如表9所示。三组表面粗糙度图如表10所示。

由表8可得,铣削力最小可达到108.449 3 N,同时表面粗糙可达Ra=0.959 4，由表9可得，所选参数试验组铣削力的预测值与实测值最大误差为10.384 7%，表面粗糙度预测值与实际值最大误差为6.222 3%，材料去除率最大值为0.639 0 cm3。与正交试验组数据进行对比，从遗传算法解集中选择的参数组其铣削力、表面粗糙度、材料去除率均在适中水平，在保证了小切削力的基础上，亦得较好的加工效率，同时观察对比表10与表4发现，其表面质量也得到了保障，达到了预期的试验目的。进一步证明了该算法的可行性与结果的可靠性。

表8 预测结果Table 8 Predict the outcome

表9 预测值与实际值对比Table 9 Comparison between predicted value and actual value

5 结论

(1)基于本次正交试验，通过极差分析可得，铣削参数对TC4钛合金铣削力的影响中，对铣削力影的主次顺序为：ap>ae>n>vf；对表面粗糙度影响的主次顺序为：vf>ae>ap>n；对材料去除率影响的主次顺序为：ap>ae>vf>n。

(2)根据正交试验数据结果建立得到铣削力与表面粗糙度的回归模型，经检验，回归模型可以使用。

(3)针对三目标优化模型，在pareto算法的基础上，相比以往双目标优化方法，减少了求解次数与参数选取时的工作量，并通过实际试验证明了该方法的可行性。