衡水湖湖面蒸发模拟在水位预测中的应用

吴景峰，刘 彬

(1.河北工程大学水利水电学院，邯郸 056038；2.河北省衡水水文勘测研究中心，衡水 053000)

近五十年来，华北平原气温呈现显著波动上升趋势，而水面蒸发量则呈总体下降、且年际变化量呈显著增大的趋势[1-2]。湖泊水位变化是生态环境的主要控制要素，对鸟类栖息和繁殖极为重要。湖体水环境的维护和生态系统的维系也均需要考虑湖面水位的变化过程。湖面蒸发过程模拟精度是湖面水位模拟和预测精度控制的关键环节[3-4]。

目前，湖面蒸发模拟方法可以分为通量模型[5-6]、蒸发成因类比模型[7-10]和能量—蒸发量转化动力学模型[11-14]三大类。通量模型利用涡度等相关理论与技术，确定湖泊的潜热通量，在此基础上直接模拟湖面蒸发过程；蒸发成因类比模型依据陆上水面蒸发场中大型蒸发池(20 m2或100 m2)的资料或漂浮水面蒸发场的资料，通过相关性分析建立与湖面蒸发量的关系。动力学模型主要包括Penman模型、质量转移模型和Dalton模型等，考虑湖表层能量平衡过程和湖体垂直水温扩散过程中能量和质量均衡与蒸发通量传输关系，并结合研究区的气候、地理条件对模型参数进行修正，对湖面蒸发量进行模拟。然而，衡水湖包括了水面(33.2 km2)和湖体植被(9.35 km2)两种蒸发面，边界条件影响下的能量平衡和水均衡机制与三类模型的蒸发模拟机制有显著的差异性，在机理上不满足衡水湖湖面蒸发预报动态模拟的需求。针对这一问题，开展了3年的现场实验，基于水量平衡法[15]测定了衡水湖蒸发量，基于蒸发动力学原理发展了适用于水生植物覆盖和水面条件下衡水湖的蒸发物理模型，并采用Sobol全局性敏感性分析方法[16-17]，分析了模型中辐射项、空气动力学项、阻力项、以及下垫面对湖面蒸发量的敏感程度，旨在为衡水湖水位精准预报提供理论和方法支撑。

1 材料和方法

1.1 研究区概况

衡水湖(115°27′50″E～115°42′51″E，37°31′40″N～37°41′56″N)属于海河流域子牙河水系，湖泊面积75 km2，是华北平原惟一保持沼泽、水域、滩涂、草甸和森林等完整湿地生态系统的自然保护区，生物多样性十分丰富。衡水湖所有入湖口均设有闸门，使衡水湖成为与河渠没有直接水循环联系的“独立”湖泊。1994年11月“引黄入冀”工程完工后衡水湖得以引水入湖，至今才未干涸过。2018—2020年衡水湖共引水1.54×108m3；衡水湖出水量主要为湖区供给衡水发电厂用水。水文测区包含衡水湖水文站，王口站、南关站两个入湖闸流量站，衡水湖电厂取水口监测站，冀州站、巨鹿站两个湖边气象站，衡水湖基本情况如图1所示。

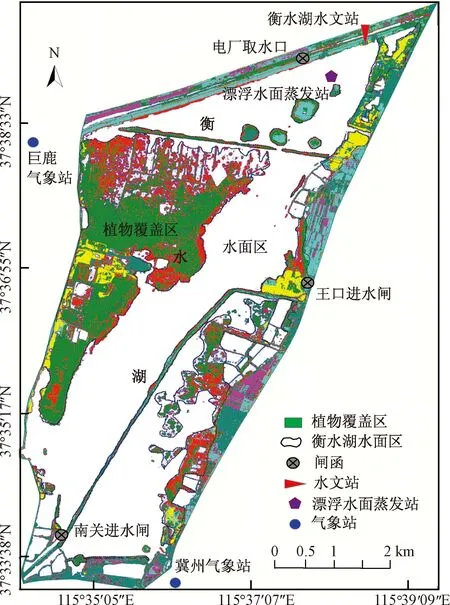
图1 衡水湖基本信息Fig.1 Basic information of the Hengshui Lake

衡水湖年平均气温12.7 ℃；一月份最冷，月平均气温-3.1 ℃；7月份最热，月平均气温26.9 ℃。最低气温为-23.0 ℃，最高气温为42.7 ℃。年均降水量为490.7 mm，无霜期191 d，日照时数2 642.8 h。

1.2 衡水湖蒸发实验

湖面蒸发量采用水量平衡法测定。2018—2020年，对衡水湖的水量平衡要素，包括水位变化、入出湖径流过程、降水以及湖底渗漏等湖体水量平衡过程进行了测量。湖面蒸发量计算公式为

El=103(Zt-Zt+1)+10(Win-Wout-Lp)/A+P

(1)

式(1)中：El为湖面蒸发量，mm；Zt、Zt+1分别为t和t+1时刻的湖水位，m；Win和Wout分别为地表径流入流量和出流量，104m3，入流量基于入湖闸流量站测定，出流量为工业取水量，由衡水湖电厂取水口监测站测定；Lp为湖体渗漏量，104m3，2013—2018年长系列监测资料表明，衡水湖逐日渗漏较为稳定，衡水湖多年平均单位面积渗漏量为37.5×104m3/(km2·a)，范围在34.6×104～42.4×104m3/(km2·a)，极值差为7.8×104m3/(km2·a)，极值比为1.23[18]，即单位面积的渗漏量为1.03 mm/d，变化量为0.21 mm/d，渗漏的变化量仅为湖面蒸发量均值的3.34%，对于衡水湖的日蒸发量精度的影响非常有限；A为相应湖面面积，km，根据水位～湖面面积曲线确定；P为降水量，mm。

实验期采用水量平衡法测定的衡水湖蒸发量年均为1 031.1 mm，3—12月蒸发量为986.4 mm，与漂浮水面蒸发场测定的水面蒸发量925.1 mm(3—12月)的比值如表1所示，可以看出，湖面植物生长的旺季(7—8月)，湖面蒸发量和水面蒸发量比值为1.14，超过了植物生长期(5—10月)的比值1.08，以及植物非生长期比值0.99。表明挺水植物生长期(5—10月)增加了整个湖面蒸发量的8%。

表1 湖面蒸发量与水面蒸发量的比值Table 1 The ratio of lake surface evaporation to water surface evaporation

衡水湖植被覆盖区和水面区如图1所示。遥感技术是高时效、高精度获取地球表面区域蒸散发最有效的方法[19-20]。实验期(2018—2020年)通过SPOT6与高分一号卫星获取遥感土地利用分类的影像，以2019年6月SPOT6影像、2019年8—10月哨兵二号影像、2020年7月高分一号影像为主要遥感数据源，用遥感方法测定湖水面区域和植被覆盖区域[21]。测定了湖中植物覆盖区植物的物候、生物和生理参数，测定时间间隔为15～30 d。衡水湖湿地水生植被以芦苇为主，芦苇面积占水生植被总面积80%以上。

1.3 模型构建

1.3.1 模型推导

根据能量平衡原理，湖面接收的辐射能转化为湖面蒸发所形成的潜热消耗、湖水温度变化所吸收的能量和由于湖面和大气温度差形成的显热消耗，能量平衡方程为

Rn=Hl+LEl+WG

(2)

式(2)中：Rn为到达湖面的辐射能，W/m2；Hl为由于湖水温度Tl和大气温度Ta之间的温度差所形成的显热消耗，W/m2；LEl为湖面蒸发潜热消耗，W/m2，其中，L为能量和质量转换系数，取2.49 J/g；El为湖面蒸发量，mm/d；WG为湖水由于温度变化吸收的能量，W/m2。

湖面蒸发(水面蒸发和挺水植物蒸散发)包括湖面水体的汽化过程以及蒸发面水汽的扩散过程。

第一个物理过程，水面和挺水植物两种蒸发面情况下，湖面水体的汽化过程均可表示为饱和水汽压和实际水汽压之间的势能差作用下的汽化过程，受到湖面阻力的作用，可表示为

(3)

式(3)中：ρ为空气密度，kg/m3；cp为恒压下空气比热，J/(kg·K)；γ为温度计常数，hPa/℃；e*(Tl)为湖面温度下的饱和水汽压，hPa；Tl为湖水温度，℃；ec为实际水汽压，hPa；rl为湖面阻力，s/m。

第二个物理过程，水面和挺水植物两种蒸发面情况下，湖面气态水向大气中的扩散过程，可表示为

(4)

式(4)中：ea大气水汽压，hPa；rav为水汽在湖面-大气之间扩散的空气动力学阻力(s/m)。

由于湖水温度和大气温度之间的温度差所形成的显热消耗为[22]

(5)

式(5)中：Ta为大气温度，℃。

湖面温度下的饱和水汽压，是利用大气温度下的饱和水汽压和水汽压-温度曲线斜率Δ与湖水温度Tl和大气温度Ta差乘积之和进行近似，可表示为[23]

e*(Tl)=e*(Ta)+Δ(Tl-Ta)

(6)

式(6)中：e*(Ta)为大气温度下的饱和水汽压，hPa；Δ为水汽压-温度曲线斜率。

联立式(2)～式(6)，得湖面蒸发的动力学方程为

(7)

1.3.2 能量项计算

到达湖面的辐射能Rn表示为[22]

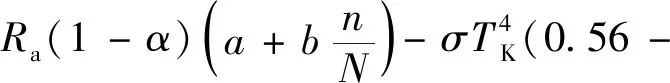
(8)

(9)

式中：Ra为大气上界的太阳辐射量，W/m2；Io为太阳常数，取8.36×104J/(m2·min)；td为一天内的时间，取1 440 min；R为日地平均距离比；Wo为时角，rad；φ为衡水湖所在的地理纬度，rad；δ为计算日赤纬，rad；α为下垫面反射系数，衡水湖湖面的反射系数为0.125；a、b为经验常数，在衡水湖分别为0.25和0.55；n为计算地点实测日照时数，h；N为天文上可照时数，h；σ为Stafen-Boltzman常数，取4.863×10-3J/(m2·d·K4)；TK为日平均气温，K。

湖体中能量的变化WG为[24]

WG=λ(Vl,i+1Tl,i+1-Vl,iTl,i)

(10)

式(10)中：λ为湖水的体积热容量，取42.6 J/(m3·K)；Vl为湖水的体积，m3；Tl为湖水温度，℃；下标i和i+1分别为当日和下一日。

式(8)、式(9)中各参数的计算公式为

δ=23.5sin(0.986m-78.9)

(11)

R=1+0.016sin[(0.523 6m-64.854)/30.0]

(12)

Wo=7.5N

(13)

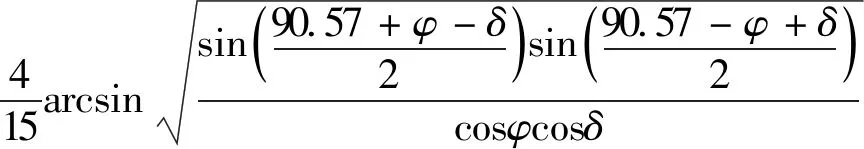
(14)

式中：m为从1月1日起到计算日天数。

1.3.3 阻力项计算

湖面阻力反映湖体水面汽化过程中所受到的阻力。对于挺水植物覆盖区，包括了植物本身的蒸散发以及挺水植物覆盖湖面对湖水蒸发的影响，阻力随湖面植物覆盖程度的增加而增大，对于水面，则主要受到水体波动的影响，湖面面积变化后，湖面气象条件对湖水汽化的影响程度增加，湖面阻力增加。考虑到以上物理特性，将湖面阻力表示为湖面面积、湖面挺水植物叶面积指数的非线性关系函数，表达式为

rl=rlmax(La/LAmax)-bl

(15)

rlmax=(fPcl+1)-blrs

(16)

式中：rlmax为最大湖面阻力，s/m；La为计算日湖面实际面积，km2(由遥感影像确定)；LAmax为湖面最大面积，km2(由实测资料确定)；f为植物覆盖区所占的比重(由实测资料确定)；P为植物覆盖区叶面积指数(由遥感实测资料确定)；rs为水面汽化阻力，s/m；cl和bl分别为反映湖面阻力随植物覆盖面积和湖面面积变化的参数。

空气动力学阻力主要受边界层条件和空气传输能力的影响，可表示为[25]

rav=ram+a(uz/ram)b

(17)

式(17)中：ram为动量传输的边界层阻力，s/m，考虑到影响水汽蒸发与扩散的条件，对于水面，表示为表面粗糙度的函数；uz为湖面参照高度(2 m)风速，m/s；a、b为反映水汽蒸发和扩散条件的系数。

(18)

式(18)中：zo为表面粗糙度，μm；k为反映植物对水汽蒸发与扩散影响的系数。

对于挺水植物覆盖面，ram为植物高度z的函数。

(19)

式(19)中：d为零平面位移，m。

可以看出，所构建的模型能够考虑湖面水面和植物覆盖面蒸发物理机制，结合动力学方法基于气象参数和湖面现状(库容)，模拟湖面蒸发的动态过程，并且能够在常规气象预报的基础上，预测衡水湖蒸发量。

1.4 基于Sobol全局性方法的衡水湖蒸发影响因素敏感性分析

分析气象因子、湖面影响阻力的各种因子对模拟结果的敏感性，有助于提高预报水平和预警决策能力。Sobol方法基于方差分解，将目标函数的总方差分解为单个参数的方差和参数间相互作用的方法，实现参数的全局性敏感性分析。

选择温度、风速和日照时数3个气象因子，表面粗糙度、零平面位置、k和a4个空气动力学因子，以及湖面面积，共8个因子进行敏感性分析，具体方法如下。

采用Monte Carlo方法，随机产生2个不同的低差异的随机参数矩阵，其表达式分别为

(20)

(21)

式中：m′为矩阵行数；n′=8为影响因子的数量参数个数。

A和B这2个随机序列具有不同的均值和标准差，利用矩阵B中的第i列数据(影响因子xi的抽样值)替换矩阵A中的第i列数据(影响因子xi的抽样值)形成一个新的联合矩阵Ci。

i=1,2,…,n′

(22)

对每一个影响因子都生成一个联合矩阵，作为参数，基于式(22)计算各影响因子xi的一阶敏感性Si和总敏感性指数STi，其计算公式分别为

(23)

(24)

2 结果与讨论

2.1 参数率定

采用式(7)对衡水湖整个湖面的蒸发量进行逐日计算，计算所需要的气象参数(日均温度、风速、水汽压、日照时数等)根据湖边气象站和水面漂浮气象站的实测值，采用Theis加权平均法确定。湖面面积等参数根据水位-面积曲线等衡水湖参数确定，需率定的参数包括湖面植物和水面计算动量传输边界层阻力计算参数(表面粗糙度zo、零平面位移d和k等)，空气动力学项计算参数a、b，以及植物覆盖面和水面2种蒸发面参数cl、bl。采用2018年、2019年监测数据，设定目标函数为

(25)

以湖面蒸发量模拟值和实测值的相对均方根误差最小为目标函数，参数率定结果如表2所示。采用2020年实测资料对参数的计算精度进行了检验。

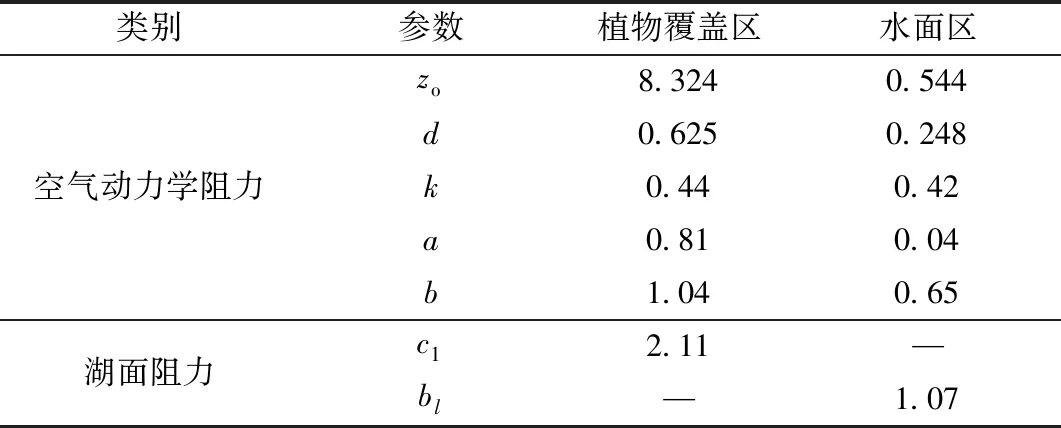
表2 率定参数Table 2 Calibrated parameters

2.2 模拟分析

图2为模拟和实测逐日湖面蒸发量的比较，其中2018年、2019年为参数率定期，2020年为模型验证期。参数率定期的实测和模拟蒸发量的均值分别为3.22、3.08 mm/d，相对偏差为4.35%，蒸发量的变换范围分别为[0.22,9.88] mm/d和[0.18,8.24] mm/d，模拟的最大值相比实测值偏小16.6%。在模型验证期，实测和模拟的蒸发量平均值分别为3.43、3.41 mm/d，偏差小于1%，变化范围分别为[0.28,9.14] mm/d和[0.17,9.25] mm/d，偏差小于5%。可以看出，模拟蒸发量与实测值表现出较高的一致性。

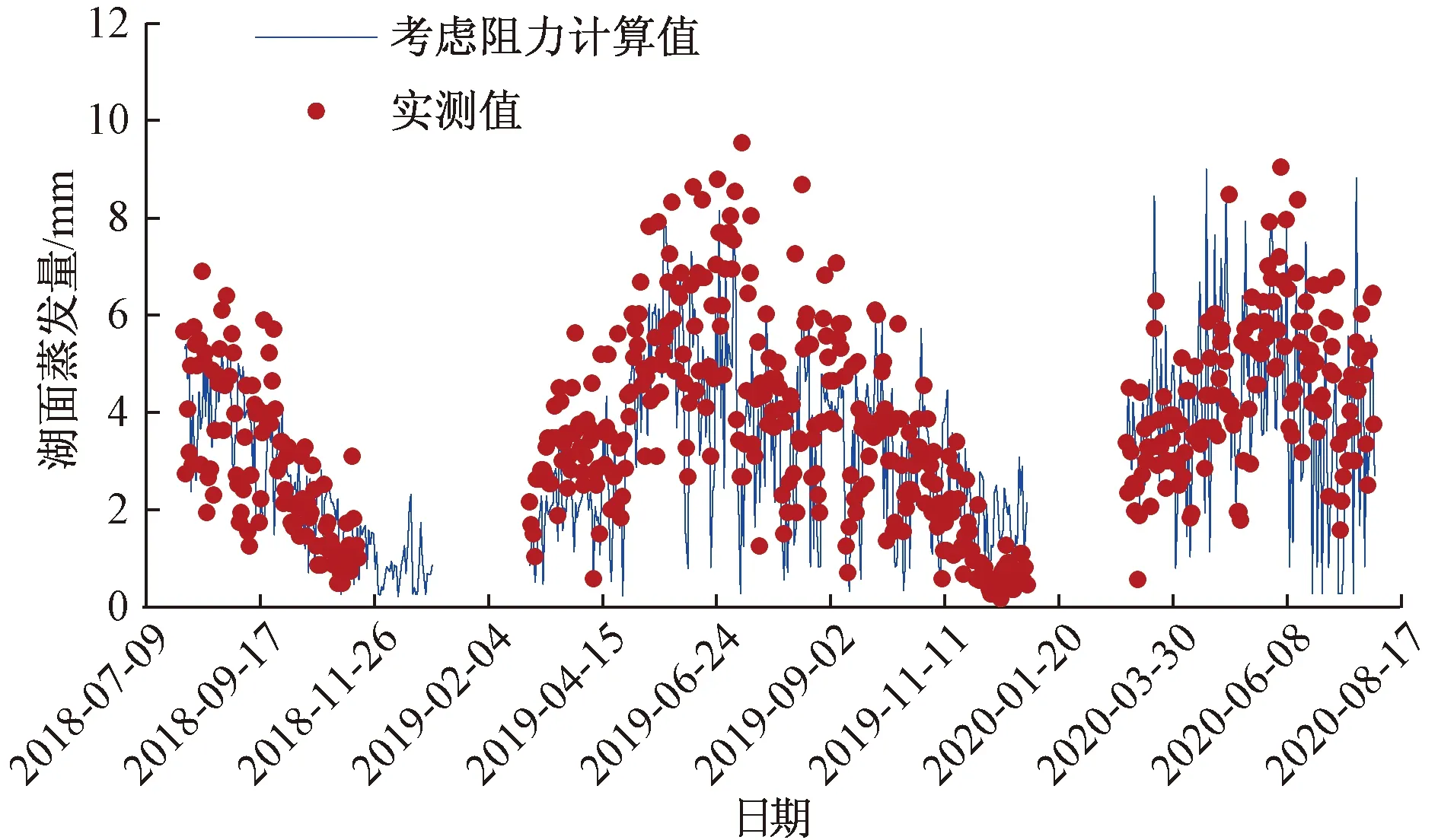
图2 模拟和测定的湖面蒸发量比较Fig.2 Comparisons of simulated and monitored lake evaporation

参数率定期和验证期湖面蒸发量的纳什效率系数(Nash-Sutcliffe efficiency coefficient，NSE)分别为0.744和0.687。表明模型经过参数率定后，能够模拟湖面蒸发过程，所提出的方法准确地模拟了衡水湖蒸发变化的趋势性和范围，具有较高的准确性。

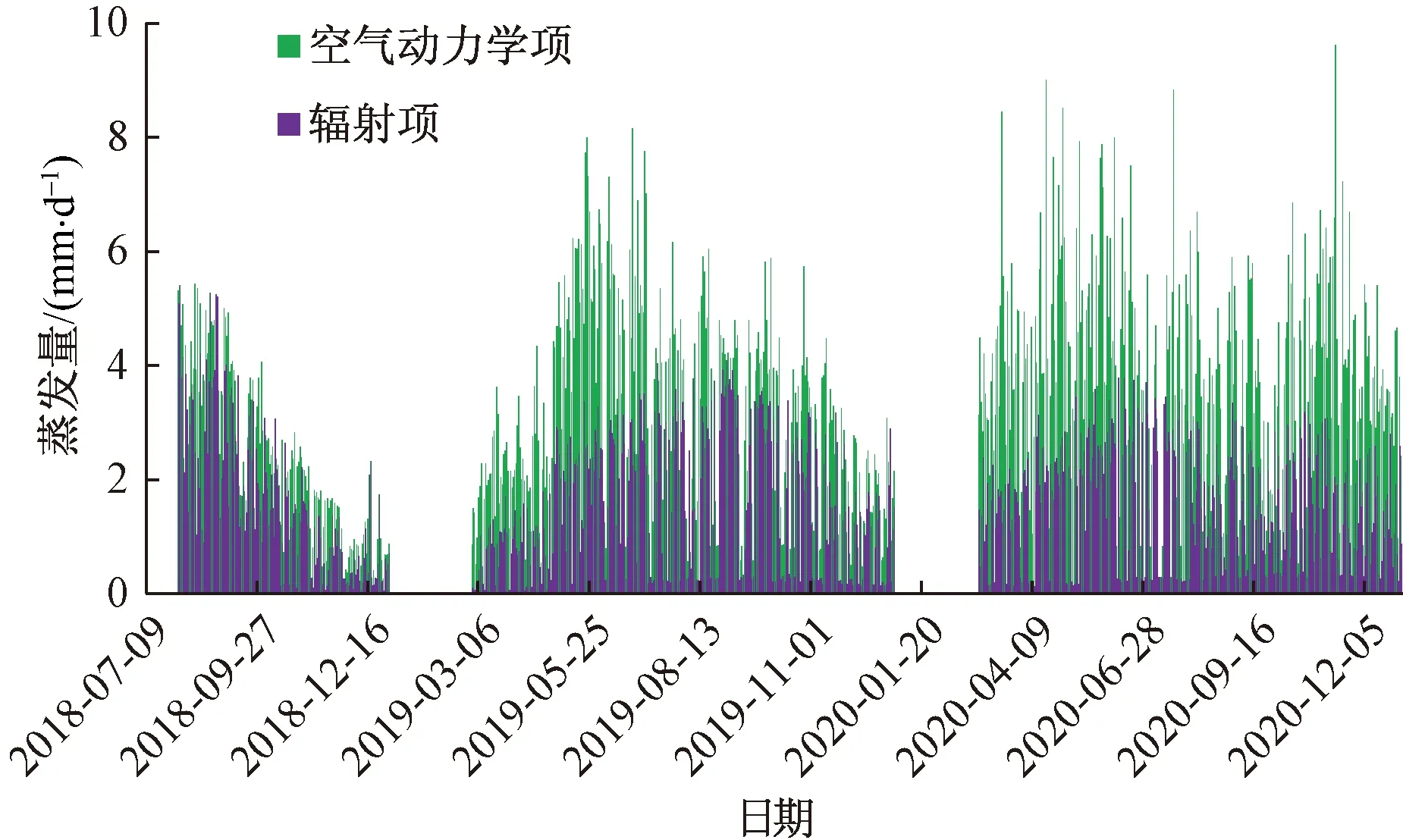
图3 空气动力学项和辐射项对湖面蒸发量的影响Fig.3 The impacts of radio and the air dynamic on the lake evaporation

2.3 敏感性分析

参数的Sobol一阶和总敏感性指数如表3所示。气象因子、阻力因子和湖面因子3种影响湖面蒸发的因子中，气象因子的一阶敏感性指数均值为0.118，显著高于阻力(空气动力学阻力和水面阻力)的一阶敏感指数的均值(0.028)，表明多因子作用条件下，气象因子为衡水湖最敏感因子，而湖面因子的影响最小。

表3 衡水湖湖面蒸发影响因子敏感性分析Table 3 Sensitivity analysis of the factors affecting Hengshui Lake evaporation

3个气象因子和3个阻力因子的总敏感性指数超过0.1，达到显著水平。表明湖面蒸发是气象和阻力多因子作用表现出的非线性响应特性。各因子中，辐射(日照时数)和温度的一阶敏感性指数、总敏感性指数与一阶敏感性指数的差异性在8个因子中是最大的，表明这两个因子与其他因素之间交互影响的敏感性最为显著，衡水湖属于平原区宽浅湖泊，多数时间都是定期引水，不存在对流交换影响，因此能量传输和水温在垂线的分布比较均匀，湖面在垂线方向上没有明显的阶梯变化，因而辐射、温度与其他因子之间的交互敏感性影响最大。而湖面因子与其他因子的交互敏感性的影响最小。

2.4 湖面蒸发模拟在衡水湖水位预测中的应用

水位是湿地生态系统健康发展的重要指标。开展水位变化预测对指导衡水湖科学调水，合理开发利用湖水资源，改善衡水湖生态环境，调控引水量将水位控制在合理的范围内，保持衡水湖湿地生态系统长期健康具有重要意义。

1994—2020年，衡水湖年均水位保持在18.67～20.76 m，多年平均水位为19.95 m。根据《河北省衡水市水情预警发布管理办法(试行)》，衡水湖湖内水位达到或低于19.50 m，为蓝色预警；达到或低于19.00 m，为黄色预警；达到或低于18.65 m，为橙色预警；达到或低于18.30 m为红色预警。根据 2020年的验证期衡水湖蒸发量模拟结果，采用式(1)原理预测水位变化，和实测水位变化的比较如表4所示。可以看出，月模拟水位与实际水位绝对误差最大为-4 cm，小于2020年衡水湖水位变幅58 cm的20%许可误差12 cm，合格率为100%；计算确定性系数为0.98，大于0.90。预报精度从合格率和确定性系数均达到甲级，表明模型法能够较好地预测衡水湖水位动态。

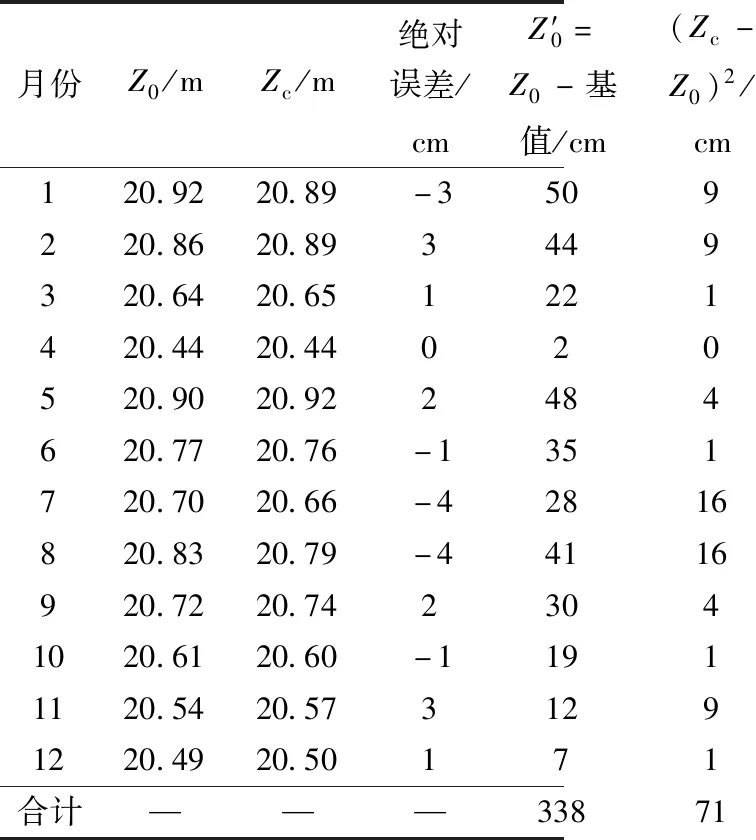
表4 衡水湖2020年水位模拟结果比较Table 4 Comparison of the simulated and monitored water level in 2020

每年的4—6月是鸟类的繁殖期，也就是水位预测的关键期。从表4中可以看出，在12个月中，4—6月的水位模拟结果相比其他月份，有更好的符合度，满足衡水湖生态对于水位预测的需求。

3 结论

(1)2018—2020年，测定了衡水湖入出径流量、水位、降水量和湖底渗漏量等水文变化过程，基于水量平衡法测定了湖面蒸发量为1 031.1 mm(1—12月)，与漂浮蒸发站测定的水面蒸发量925.1 mm(3—12月)进行月对比，数据可靠性高。

(2)提出了基于动力学原理，发展了湖面植物覆盖和水面两种蒸发条件下的空气动力学阻力和下垫面阻力计算方法，提出了衡水湖蒸发量计算方法，采用实测资料进行了参数率定和模型验证，模型验证期模拟结果和实测结果的NSE为0.687，所提出的方法能够有效地模拟衡水湖湖面蒸发过程。

(3)采用Sobol一阶敏感性指数和总敏感性指数进行的参数敏感性分析表明，气象因子对衡水湖水面蒸发的敏感性显著的超过了空气动力学因子和湖面因子，其中辐射、温度与其他因子的交互敏感性最为显著。

(4)验证期将模型应用于水位预测表明，所提出的衡水湖蒸发量计算方法满足衡水湖水位预警和生态预报的精度要求，具有较高的精度。