与广义二次矩阵相关的广义Jordan积秩的不变性

吕洪斌, 陈梅香, 杨忠鹏, 冯晓霞

( 1.北华大学 数学与统计学院, 吉林 吉林 132013； 2.莆田学院 数学与金融学院, 福建 莆田 351100；3.闽南师范大学 数学与统计学院, 福建 漳州 363000 )

0 引言

设Cm ×n为复数域C上的m×n阶矩阵集合,r(A)表示A∈Cm ×n的秩,I表示单位矩阵,It表示t×t阶单位矩阵,矩阵X(1)为矩阵X的满足XX(1)X=X的广义逆.记Γ={(a,b):a+b≠0,ab≠0;a,b∈C}.

设A,B∈Cn ×n, 称AB+BA为矩阵A与B的Jordan积[1].Tian等研究了幂等矩阵P与Q的Jordan积的秩[2-5]； Koliha等给出了PQ+QP可逆性的充要条件[6].Tian等[2]从秩的不变性角度得到:

r(aPQ+bQP)=r(PQ+QP),P2=P,Q2=Q, (a,b)∈Γ.

(1)

Tian还研究了P和Q为幂等矩阵、C∈Cm ×n的r(PC+CQ)的更一般情况[5]:

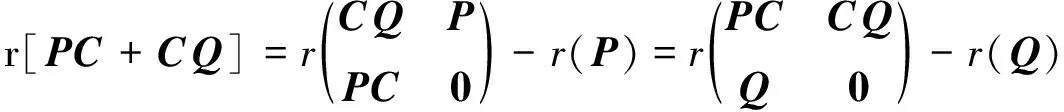
(2)

(3)

由于当P=Q时,PC+CQ=PC+CP为矩阵P与C的Jordan积,所以称PC+CQ为矩阵P、Q与C的广义Jordan积[7].

若有λ(≠0)∈C使P2=λP, 则称P是由λ确定的数量幂等矩阵[3].文献[4,8-9]的作者给出了这类矩阵的相关性质.

若dA,eA∈C使(A-dAI)(A-eAI)=0, 则称A∈Cn ×n为由dA和eA确定的二次矩阵[10-13].二次矩阵在随机理论、微分方程、量子力学等领域有着重要应用.对于二次矩阵A, 当eA=0时,A为由dA确定的数量幂等矩阵；若还有dA=1, 则A为幂等矩阵.当dA=-eA≠0时,A是数量对合矩阵[14],且当dA=-eA=±1时,A为对合矩阵.2005年, Farebrother等给出了如下广义二次矩阵的概念[15]:对给定的幂等矩阵P, 若AP=PA=A且有α,β∈C使得A2=αA+βP, 则称A∈Cn ×n为由幂等矩阵P确定的广义二次矩阵.文献[12,16-17]的作者给出了如下广义二次矩阵的定义：对给定的幂等矩阵P, 若AP=PA=A且有d,e∈C使(A-dP)(A-eP)=0, 则称A∈Cn ×n为由d和e确定的广义二次矩阵.由(A-dP)(A-eP)=A2-(d+e)A+deP以及文献[16]可知,文献[12,16-17]中的关于广义二次矩阵的定义与文献[15]中的定义是等价的.因此,本文记

Ωn(P;d,e)={A∈Cn ×n: (A-dP)(A-eP)=0,AP=PA=A},

(4)

进而可记所有由幂等矩阵P确定的广义二次矩阵的集合为：

(5)

由式(4)、(5)知广义二次矩阵是比二次矩阵(相应于分别记为Ωn(I;d,e),Ωn(I))更为广泛的矩阵类.

由文献[18,例1]知有二次矩阵

和式(4)、(5)可知A∈Ω4(P), 但A∉Ω4(Q), 即A是由幂等矩阵P所确定的广义二次矩阵,但非由幂等矩阵Q确定的广义二次矩阵.

例1说明广义二次矩阵A∈Ωn(P;dA,eA)和B∈Ωn(Q;dB,eB)比二次矩阵更为复杂.对给定的幂等矩阵P和Q, 本文研究与广义二次矩阵A∈Ωn(P;dA,eA)和B∈Ωn(Q;dB,eB)相关的广义Jordan积的秩的不变性.本文结果可改进文献[7]中与二次矩阵相关的基本结论.

1 预备知识

引理1设A∈Cm ×n, 则对任意的非零复数λ、a和b有:

(6)

由式(4)、(5)可得如下引理：

引理2设P为给定的幂等矩阵,A∈Cn ×n且AP=PA=A, 则A∈Ωn(P) ⟺存在dA,eA∈C使得(A-dAP)(A-eAP)=0.

当A∈Ωn(P;dA,eA)且dA=eA时,由式(4)和式(5)可知(A-dAP)2=0, 即A是广义二次幂零的.因此，不失一般性,当A∈Ωn(P)时总约定dA≠eA.

引理3设P2=P∈Cn ×n,A∈Cn ×n且AP=PA=A, 则有可逆矩阵G与W, 且使得：

P=Gdiag(Ir,0)G-1,r(P)=r;A=Gdiag(A1,0)G-1,A1∈Cr ×r;

(7)

A∈Ωn(P;dA,eA) ⟺A1∈Ωr(Ir;dA,eA)；

(8)

A=Wdiag(dAIt,eAIr -t,0)W-1∈Ωn(P;dA,eA),r(P)=r, 当dA≠eA时.

(9)

(A-dAP)(A-eAP)=Gdiag((A1-dAIr)(A1-eAIr),0)G-1.

(10)

于是由式(4)、(5)知式(8)成立.

引理4设P为给定的幂等矩阵,A∈Cn ×n且AP=PA=A, 则有：

2)当A∈Ωn(P;dA,eA)时,则A-dAP是由eA-dA确定的数量幂等矩阵,且A-dAP是以eA-dA和0为特征值的可对角化矩阵.

证明1)由AP=PA=A知,当dA≠eA时有：

(A-dAP)(A-eAP)=(A-dAP)[(A-dAP)-(eA-dA)P]=

2)由上述证明1)得(A-dAP)2=(eA-dA)(A-dAP), 即A-dAP是由eA-dA确定的数量幂等矩阵.再由引理3及式(8)、(9)知A-dAP是以eA-dA和0为特征值的可对角化矩阵.

引理5[20]设F∈Cm ×n,G∈Cm ×p,K∈Cq ×n, 则有：

(11)

r(F,G)=r(F)+r(G-FF(1)G)=r(G)+r(F-GG(1)F).

(12)

2 广义二次矩阵的广义Jordan积秩的不变性

定理1设C∈Cm ×n,P2=P∈Cm ×m,Q2=Q∈Cn ×n, (a,b)∈Γ, 则有：

r(aPC+bCQ)=r(PC+CQ)

(13)

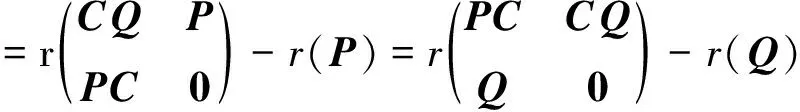
(14)

(15)

知

(16)

当(a,b)∈Γ时,由

和式(16)有

注意到

且

于是有:

(17)

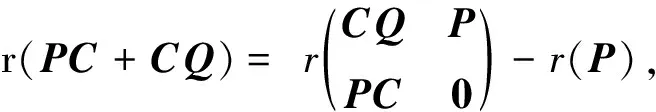
定理1说明,相对于文献[5,定理4.5]中的广义Jordan积的秩等式(2)、(3)，在约束(a,b)∈Γ之下,r(aPC+bCQ)具有不变性.

定理2设P2=P∈Cm ×m,Q2=Q∈Cn ×n,C∈Cm ×n且复数dA,eA,dB,eB∈C使得A∈Ωm(P;dA,eA),B∈Ωn(Q;dB,eB).若(a,b)∈Γ, 则有：

r[a(eB-dB)AC+b(eA-dA)CB-(a(eB-dB)dAPC+b(eA-dA)dBCQ)]=

r[(eB-dB)AC+(eA-dA)CB-((eB-dB)dAPC+(eA-dA)dBCQ)]

(18)

(19)

(20)

(21)

(22)

证明由式(10)知

(23)

注意到dA≠eA,dB≠eB的约定,据此有：

x(eB-dB)AC+y(eA-dA)CB-[x(eB-dB)dAPC+y(eA-dA)dBCQ]=

x(eB-dB)(A-dAP)C+y(eA-dA)C(B-dBQ)=

由上式可得：

r[x(eB-dB)AC+y(eA-dA)CB-(x(eB-dB)dAPC+y(eA-dA)dBCQ)]=

(24)

于是由式(13)—(15)和式(23)—(24)知,当(a,b)∈Γ且取x=a,y=b时有：

r[a(eB-dB)AC+b(eA-dA)CB-(a(eB-dB)dAPC+b(eA-dA)dBCQ)]=

r[(eB-dB)AC+(eA-dA)CB-((eB-dB)dAPC+(eA-dA)dBCQ)].

由上式可知式(18)成立.再由

由式(13)、式(14)中的第1式和式(18)知式(19)成立.

类似的由式(13)、式(14)中的第2式和式(18)知式(20)成立.再由

和式(13)-(15)、(18)、(20)知式(21)、(22)成立.

在定理2中取P=Q=In即可得到文献[7]中的基本结论(文献[7]中的式(14)).

推论1设P2=P,Q2=Q∈Cn ×n,且有复数dA,eA,dB,eB∈C使得A∈Ωn(P;dA,eA),B∈Ωn(Q;dB,eB).若(a,b)∈Γ, 则有：

r[a(eB-dB)A+b(eA-dA)B-(a(eB-dB)dAP+b(eA-dA)dBQ)]=

r[(eB-dB)A+(eA-dA)B-((eB-dB)dAP+(eA-dA)dBQ)]

(25)

(26)

(27)

(28)

=r[A-dAP]+r[((eA-dA)I-(A-dAP))(B-dBQ)((eA-dA)I-(A-dAP))]

(29)

=r[B-dBQ]+r[((eB-dB)I-(B-dBQ))(A-dAP)((eB-dB)I-(B-dBQ))].

(30)

((eA-dA)I-(A-dAP))(B-dBQ)(I-(A-dAP)(1)(A-dAP))=

(31)

(I-(B-dBQ)(1)(B-dBQ))(A-dAP)((eB-dB)I-(B-dBQ))=

(32)

于是由式(11)、(12)、(31)和式(32)有：

r[A-dAP]+r[((eA-dA)I-(A-dAP))(B-dBQ)((eA-dA)I-(A-dAP))],

r[B-dBQ]+r[((eB-dB)I-(B-dBQ))(A-dAP)((eB-dB)I-(B-dBQ))].

再由式(27)、(28)可得式(29)、(30)成立.

在推论1中取P=Q=In即可得文献[7]中的基本结论(文献[7]中的式(27)).

在定理2中取A=B即可得广义二次矩阵与任意矩阵的广义Jordan积的秩的不变性.

推论2设P2=P∈Cn ×n,C∈Cn ×n， 且有复数dA,eA∈C使得A∈Ωn(P;dA,eA).若(a,b)∈Γ, 则有：

r[aAC+bCA-dA(aPC+bCP)]=r[AC+CA-dA(PC+CP)]

(33)

(34)

(35)

证明在定理2中取A=B, 由此得P=Q, 于是由式(18)可得式(33)成立.再由式(19)、(21)可得式(34)、(35)成立.

文献[3]给出了与数量λ和μ有关的数量幂等矩阵A与B的和、差、换位子、 Jordan积的秩等式，文献[9]得到了与数量λ和μ无关的数量幂等矩阵的秩等式.以下本文将给出数量幂等矩阵与任意矩阵线性组合的Jordan积的秩不变性.

定理3设A∈Cn ×n是由非零数e确定的数量幂等矩阵,即A2=eA，C∈Cn ×n, 则有：

(36)

式(36)说明数量幂等矩阵A(即A2=eA)与任意矩阵的Jordan积的秩等式的不变性不仅与组合系数无关,而且与数e也无关.因此，定理3推广和改进了文献[2]中定理9的结论.