RV减速器摆线轮组合修形及优化
张哲衍, 柳 丽*, 罗利敏, 李国平, 莫绪伦
RV减速器摆线轮组合修形及优化
张哲衍1, 柳 丽1*, 罗利敏2, 李国平1, 莫绪伦2
(1.宁波大学 浙江省零件轧制成形技术研究重点实验室, 浙江 宁波 315211; 2.宁波中大力德智能传动股份有限公司, 浙江 宁波 315301)
为提高RV减速器的传动性能, 本文针对摆线轮齿廓的工作区域及组合修形方法等展开研究. 对应用广泛的“等距+移距”修形进行组合比较, 确定“正等距+负移距”的组合方式下初始间隙最小, 即啮合刚度最高; 分析针齿与摆线轮啮合的极限位置, 推导摆线轮的实际工作区域, 并对其采用遗传算法寻找最优修形量, 使组合修形逼近转角修形所得齿廓. 结果显示, 该方法得到的摆线轮齿廓在工作区域内更接近共轭齿廓, 且在齿顶与齿根处有合适的径向间隙, 可在提高摆线轮强度的同时有效补偿制造误差和安装误差, 对摆线轮的修形方式选择及修形量确定具有一定的借鉴意义.
摆线轮; 工作区域; 组合修形; 遗传算法; 误差补偿
RV减速器是在摆线针轮传动基础上开发的一种高精密传动装置, 具有传动比大、结构紧凑、运动精度高、刚度大、磁滞误差小和传动效率高的优点[1], 广泛应用于工业机器人、航空航天等领域[2]. 摆线轮作为RV减速器的关键传动部件, 其齿形轮廓直接影响传动精度、效率、寿命等重要性能[3]. 故研究摆线轮的最佳修形方法及修形量具有重要的现实意义.
李力行[4]阐述了摆线轮齿廓修形的3种基本方式, 即等距、移距以及转角修形. Wang等[5]通过比较不同修形组合下的初始啮合间隙大小, 探寻啮合刚度最高的组合. 于影等[6]通过分析针齿啮合的两个极限位置, 推导出摆线轮与针齿啮合的实际工作范围. Ren等[7]提出一种通过关键点来定义摆线轮修形齿廓的修形方法, 并通过数值实验验证了该方法能有效提高摆线针轮传动的承载能力. Li等[8]在修形过程中考虑压力角的影响, 提出一种新的齿廓修形数学模型.
本文综合3种基本齿廓修形方式的优点, 在摆线轮啮合刚度最大的修形组合下使实际工作区域内“等距+移距”修形所得齿廓逼近转角修形所得齿廓. 采用遗传算法对该区域齿廓直接寻优, 提高了优化效果. 通过对某企业RV20E-ASSY-81i型减速器摆线轮的优化, 验证了该方法的实用性.
1 摆线轮组合修形
1.1 摆线轮齿廓方程
与针齿共轭且无啮合间隙的摆线轮齿廓称为标准齿廓[9]. 实际应用中, 为补偿制造误差并确保良好的润滑, 必须对摆线轮轮廓进行修形. 根据摆线轮啮合及成形机理, 有如图1所示的摆线轮齿形曲线.
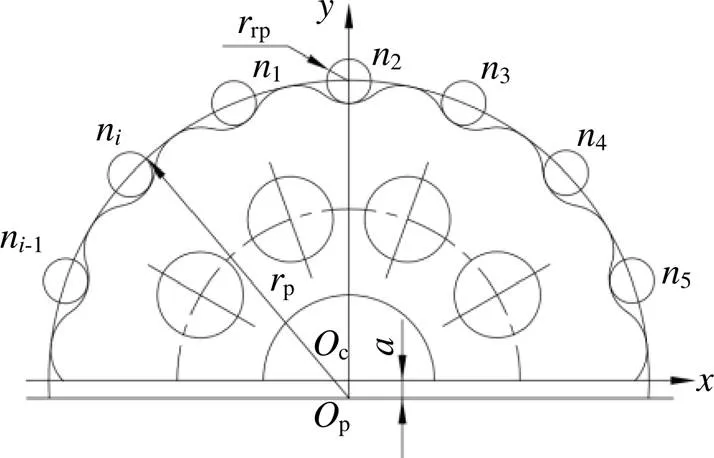
图1 摆线轮齿形曲线
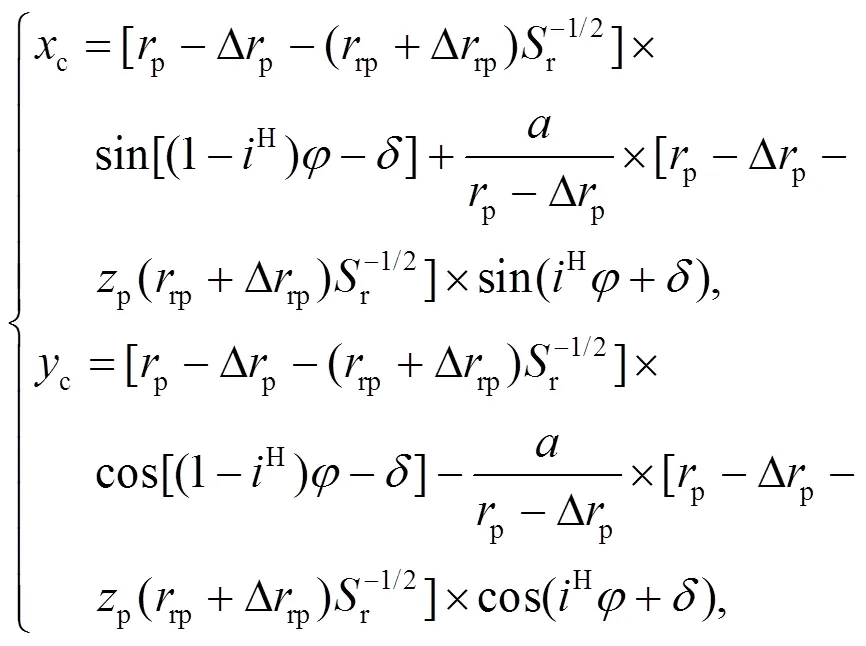
1.2 不同修形方式的初始间隙
上述3种修形方法中, 转角修形所获得的摆线轮齿廓属于共轭齿廓, 可保证传动的平稳性, 但其磨出的摆线轮在齿顶和齿根处无法产生间隙, 故不能单独使用. 而等距修形与移距修形磨削工艺简单, 且可根据具体要求获得合适的径向间隙, 故在实际应用中多采用等距、移距或其组合的方式进行齿廓修形.
摆线轮经等距、移距修形后会在其理论啮合点(标准摆线轮与针齿的啮合点)的法线方向产生初始间隙. 初始间隙的大小影响摆线轮与针齿的啮合对数, 从而影响其啮合刚度. 现分析不同修形方式的初始间隙.
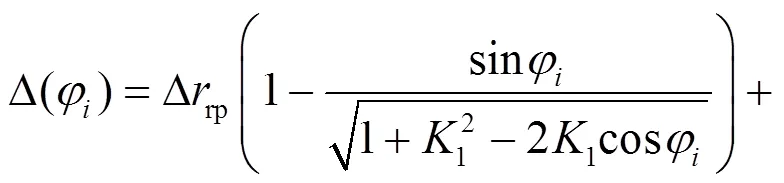
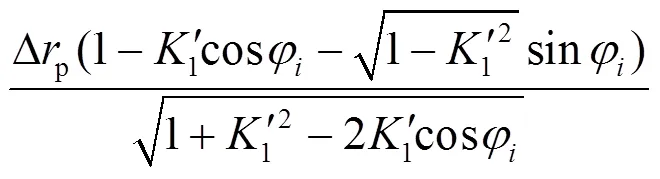
以某企业RV20E-ASSY-81i型减速器的摆线轮为例, 其基本参数见表1.
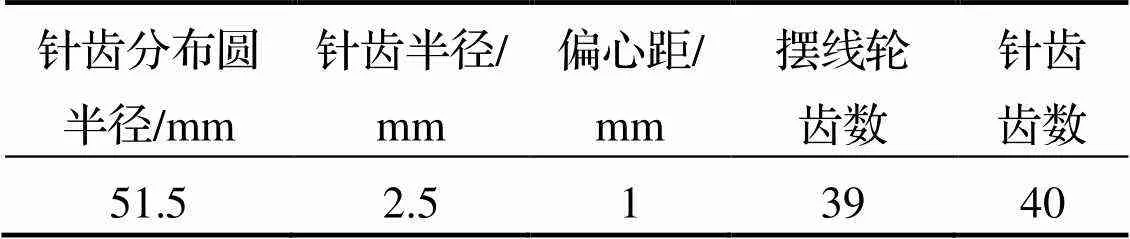
表1 RV20E-ASSY-81i型减速器摆线轮基本参数
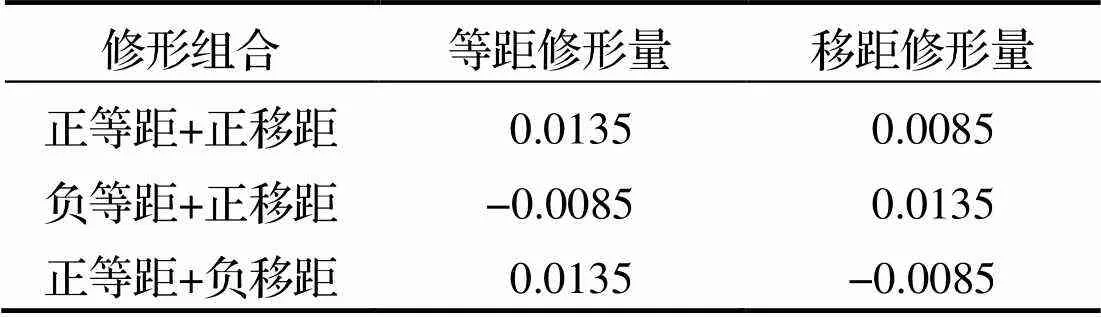
表2 不同修形组合的修形量 mm
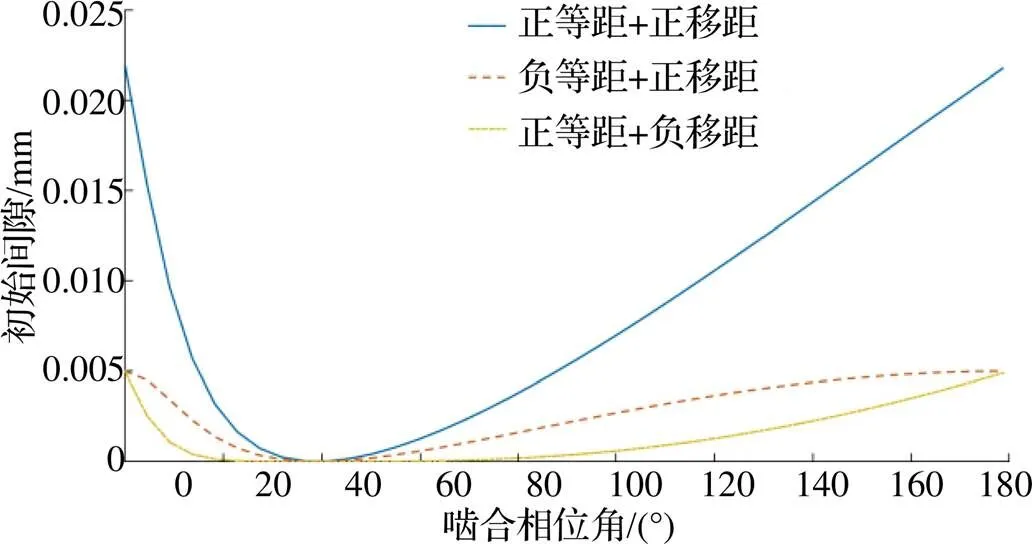
图2 不同修形组合下的初始间隙
由图2可知, 相比其他修形方式,“正等距+负移距”的修形组合可获得更小的初始啮合间隙. 更小的初始间隙不但更接近标准齿形曲线, 还可使修形后的摆线轮与针齿的啮合对数增加, 提高啮合刚度. 因此, 本文选择“正等距+负移距”的组合进行摆线轮修形.
2 摆线轮工作区域
在摆线轮的工作过程中, 并非所有齿廓都参与啮合, 因此在摆线轮齿廓修形优化之前, 需确定其工作区间, 从而确保优化结果的可靠性.
2.1 摆线轮工作区域分析
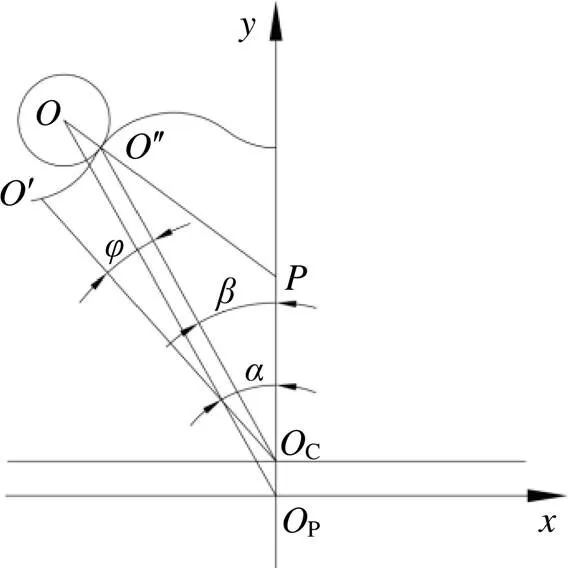
图3 摆线轮工作区域
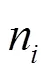
已知:
由定比分点定理可得:
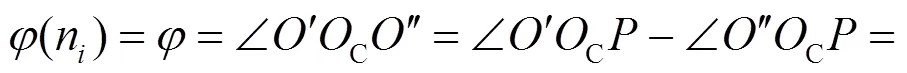
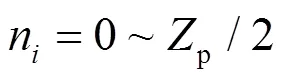
2.2 摆线轮工作区域确定
将RV20E-ASSY-81i型减速器摆线轮基本参数代入公式(3), 通过Matlab计算可得如图4所示的针齿啮合相位角函数曲线.
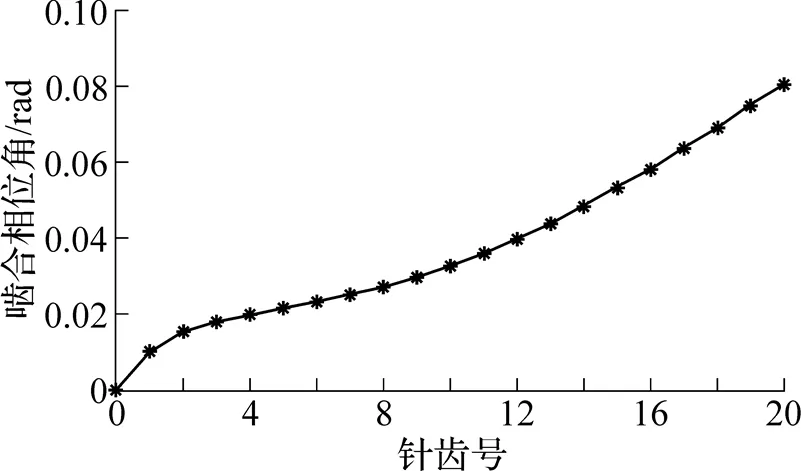
图4 啮合相位角函数曲线
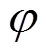
则该摆线轮的工作区域为
3 摆线轮的修形及优化
为使摆线轮齿廓的工作区域能最大限度逼近共轭齿形, 且在齿顶齿底产生径向间隙, 选择等距、移距组合修形逼近转角修形的优化方法, 结合前文研究, 组合形式为“正等距+负移距”.
3.1 设计变量及目标函数
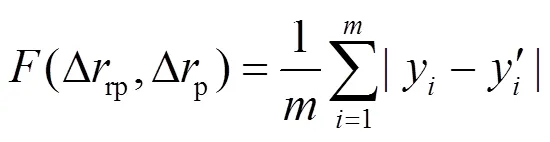
3.2 约束条件
3.3 遗传算法寻优
选择遗传算法对目标函数(4)进行寻优, 参数设置如下: 给定初始种群数目num=20, 迭代40次. 最小适应度收敛曲线如图5所示.
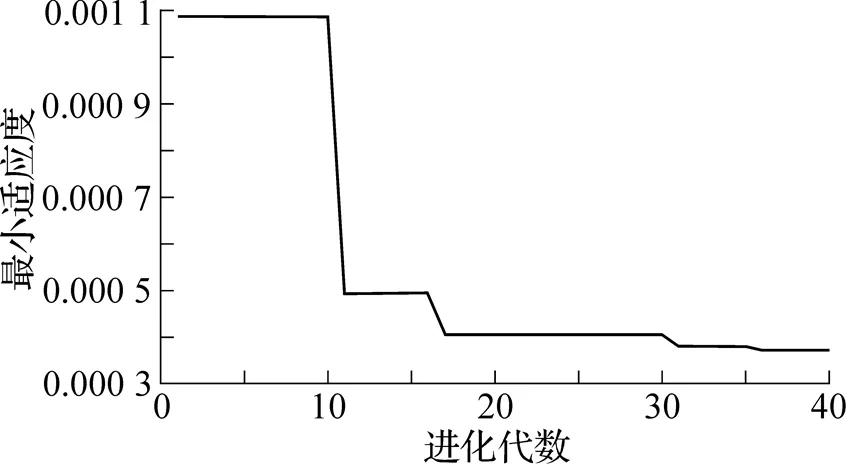
图5 组合修形优化最小适应度收敛曲线
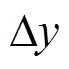
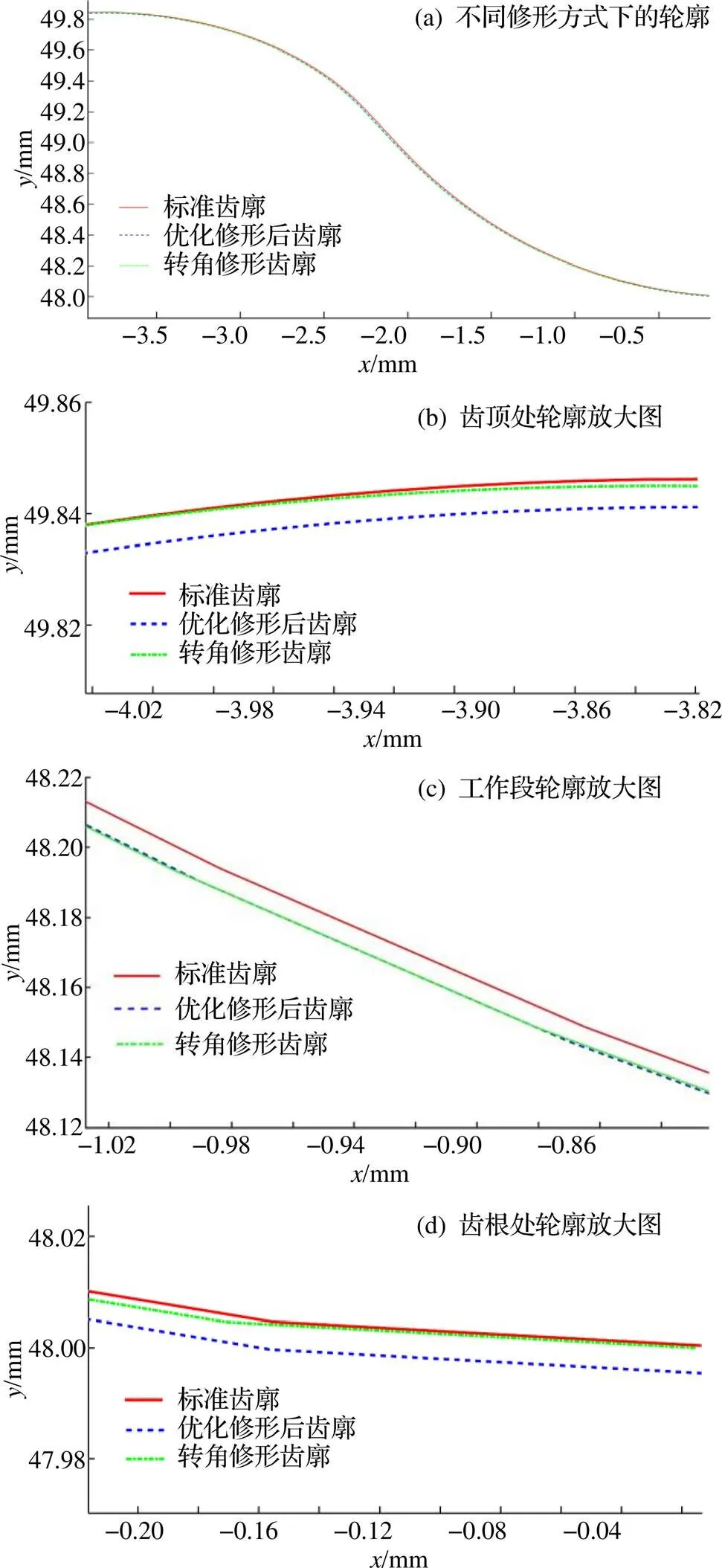
图6 摆线轮轮廓曲线
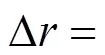
4 结论
为获得加工工艺简便、啮合刚度大、传动性能好的摆线轮齿廓, 本文做了以下研究:
(1)比较不同组合方式下摆线轮与针齿初始间隙的大小, 获得在“正等距+负移距”组合修形方式下摆线轮啮合间隙最小、啮合刚度最大的结论.
(2)推导了摆线轮工作区域的啮合相位角数学公式, 并确定工作区域大小.
(3)用“正等距+负移距”的组合修形方法来逼近转角修形的齿廓, 采用遗传算法对优化问题求解. 优化后的齿廓在工作区域更接近共轭齿廓, 且能在齿顶与齿底形成合适的径向间隙, 有效补偿制造误差及安装误差, 留下足够的润滑空间.
[1] 李力行, 何卫东, 王秀琦, 等. 机器人用高精度RV传动的研究[J]. 大连铁道学院学报, 1999, 20(2):1-11.
[2] 汪泉, 曾利磊, 秦争争. 考虑摆线轮齿廓修形的RV减速器齿轮结构多目标优化设计[J]. 机械传动, 2020, 44 (4):54-60.
[3] 魏波, 周广武, 杨荣松, 等. RV减速器摆线轮齿廓修形方法对比研究[J]. 机械设计与研究, 2016, 32(1):41- 44; 47.
[4] 李力行. 摆线针轮行星传动的齿形修正及受力分析[J]. 大连铁道学院学报, 1984, 5(4):29-40.
[5] Wang J, Gu J, Yan Y. Study on the relationship between the stiffness of RV reducer and the profile modification method of cycloid-pin wheel[C]//International Conference on Intelligent Robotics & Applications, 2016:721-735.
[6] 于影, 邵忠喜, 于波. 摆线轮啮合齿形工作范围的确定[J]. 机械设计与研究, 2006, 22(5):65-67.
[7] Ren Z Y, Mao S M, Guo W C, et al. Tooth modification and dynamic performance of the cycloidal drive[J]. Mechanical Systems and Signal Processing, 2017, 85: 857-866.
[8] Li T X, An X T, Deng X Z, et al. A new tooth profile modification method of cycloidal gears in precision reducers for robots[J]. Applied Sciences, 2020, 10(4):1266.
[9] 徐宏海, 冯玉宾, 刘学翱, 等. RV传动啮合齿形参数化设计及其软件开发[J]. 现代制造工程, 2015(1):125- 128.
[10] 程乃士. 减速器和变速器设计与选用手册[M]. 北京: 机械工业出版社, 2007.
[11] 丁国龙, 秦园, 明廷伯, 等. 基于接触应力均化的摆线轮修形方法[J]. 中国机械工程, 2019, 30(9):1081-1089.
[12] 曾德强. RV减速器摆线轮修形设计与优化[D]. 北京: 中国石油大学(北京), 2019.
[13] 秦争争, 汪泉, 赵大兴, 等. 补偿弹性变形的摆线轮齿廓修形方法[J]. 机械强度, 2020, 42(3):661-666.
Combined modification and optimization of cycloid wheel of RV reducer
ZHANG Zheyan1, LIU Li1*, LUO Limin2, LI Guoping1, MO Xulun2
( 1.Zhejiang Provincial Key Laboratory of Part Rolling Technology, Ningbo University, Ningbo 315211, China; 2.Ningbo Zhongda Leader Intelligent Transmission Co., Ltd., Ningbo 315301, China )
In order to improve the transmission performance of RV reducer, the working area of cycloid tooth profile and the combined modification method are studied in this paper. By comparing the widely used modification of “equal distance + displacement”, it is found that the initial clearance under the combination of “positive equal distance + negative displacement” is the smallest, i.e., the meshing stiffness is the highest. The limit position of the meshing between the pin tooth and the cycloid gear is analyzed, the actual working area of the cycloid gear is deduced, and the genetic algorithm is used to find the optimal modification value, so that the combined modification can approach the tooth profile obtained by the angle modification. The results show that the cycloid tooth profile obtained by this method is closer to the conjugate tooth profile in the working area, and there is an appropriate radial clearance between the tooth top and the tooth root, which can effectively compensate both the manufacturing error and the assembly error while at the same time improving the strength of the cycloid gear. It has certain reference significance for the selection of cycloid gear’s modification mode and the determination of the optimal modification value.
cycloidal wheel; working area; combined modification; genetic algorithm; error compensation
TH132
A
1001-5132(2022)01-0063-05
2021−06−07.
宁波大学学报(理工版)网址: http://journallg.nbu.edu.cn/
宁波市“科技创新2025”重大专项(2018B10007, 2019B10078, 2018B10005).
张哲衍(1995-), 男, 浙江慈溪人, 在读硕士研究生, 主要研究方向: 结构优化设计. E-mail: zhangzheyan1011@163.com
柳丽(1968-), 女, 甘肃民勤人, 副教授, 主要研究方向: 机构设计与分析等. E-mail: liuli@nbu.edu.cn
(责任编辑 韩 超)

