基于池的无监督线性回归主动学习
刘子昂 蒋 雪 伍冬睿
在机器学习任务中,往往需要大量的有标签训练数据以获得更好的性能.但是,在许多实际应用场景中,获取未标注的数据相对容易,标注过程却很困难,通常需要投入大量的时间和经济成本.例如,在语音信号的情感估计问题中,可以很容易地记录大量语音,但是要对语音进行3 个维度(愉悦度、唤醒度和优势度)的评估[1],评估者必须反复倾听,仔细检查.此外,由于情感估计具有主观性,而且部分数据可能只存在细微差异,通常需要多个评估者,例如,素材来自于德国脱口秀节目Vera am Mittag (VAM)的语料库[2]用到6~17 个评估者,国际情感数字化声音 (第2 版)(International affective digitized sounds V2,IADS-2)[3]用到至少110个评估者.在石油和天然气行业中,研究油井压裂后180 天的累计产油量预测问题[4]有利于提高采收率,输入信息(油井的压裂参数,例如油井位置、射孔长度、区域/孔的数量、注入的泥浆/水/砂的体积等)可以在压裂操作期间记录,但要获得地面产量(压裂后180 天累计产油量),至少需要等待180 天.
在很多这样的问题场景中,如何确定最优的未标注样本进行标注是非常重要的.主动学习(Active learning,AL)[5]可以用于解决此类问题,它通过选择较少的有价值样本进行标注,从而获得性能较好的机器学习模型,减少了数据标注工作.
主动学习可用于分类问题和回归问题.已有许多用于分类的AL 方法[5]相继提出,但回归任务中的AL 方法相对较少[6-20].这些主动学习回归(Active learning for regression,ALR)方法有基于流或基于池[13]的应用场景,本文考虑的是后者,即给定一个未标注样本池,ALR 需要最优地选择一些样本进行标注,从中训练出一个较好的线性回归模型.
现有的大多数基于池的ALR 方法[6-12,14-15,19-20]都考虑的是较简单的有监督场景,即能够获得少量带标签的样本,建立初始的回归模型,然后根据模型选择后续的样本交给专家进行标注.经过调研,我们只发现在4 项研究[13,16-18]中明确考虑了完全无监督的基于池的ALR 场景(将在下一节中详细介绍),即在没有任何标签信息的情况下,选择最有价值的初始样本进行标注,这也是本文的重点.
具体地说,本文考虑以下问题:在给定大小为N的未标注样本池中,如何最佳地选择初始的M个样本进行标注,从而构建较好的线性回归模型?这里的M是通过用户指定(通常,随着M变大,ALR 的优势会逐渐减弱).在本文中,我们仅关注线性回归模型.
针对上述问题,本文提出了一种基于信息性-代表性-多样性(Informativeness-representativeness-diversity,IRD)的ALR 方法.通过同时考虑主动学习中的3 个重要标准[17]:信息性、代表性和多样性,从而确定要查询的M个初始样本.在3 种不同的线性回归模型和来自不同应用领域的12 个数据集上的实验表明,与3 种已提出的ALR 方法相比,本文提出的IRD 方法所选择的M个样本可以实现更好的性能.
本文的主要贡献是:
1)提出了一种无监督的ALR 方法,同时考虑要选择的M个样本的信息性、代表性和多样性(这里M≤d+1,其中d是特征维数).根据调研,目前文献中ALR 的信息性计算都必需输出信息,还没有无需输出信息的信息性计算方法.因此,本文提出的方法是首个可考虑所选样本信息性的完全无监督ALR 方法,具有重要的理论创新性.
2)提出了一种迭代式的ALR 方法,同时考虑代表性和多样性,在M>d+1 时选择另外的M-d-1个样本.
3)在3 种常见的线性回归模型和12 个真实数据集上的大量实验,证明了所提出的IRD 方法的优越性能.
本文的组织架构如下:第1 节介绍3 种现有的无监督ALR 方法,并指出了它们的局限性;第2 节详细介绍本文提出的IRD 算法;第3 节对在12 个数据集上的实验进行了讨论和分析;最后,第4 节给出本文的结论.
1 现有的基于池的无监督ALR方法
Wu[17]提出了以下3 个基于池的有监督ALR方法应该考虑的标准.这些标准也适用于无监督的ALR 问题:
1)信息性.可以通过不确定性(熵、到决策边界的距离、预测的置信度等)、模型改变期望(Expected model change)、误差缩减期望(Expected error reduction)等来度量.
2)代表性.可以通过与目标样本相似或接近的样本数量来度量.跟目标样本相似或接近的样本越多,那么该目标样本代表性越强.此标准优先选择靠近簇中心的样本,或者分布稠密处的样本,可防止选择离群点.例如在图1 中,需要构建一个回归模型从输入x1和x2中预测输出.两个实心的点是已经选中的待标注样本,现在需要从空心的点中选出第3 个待标注样本.很显然,从包含“A”的簇中选出一个样本比选择样本“B”更好,因为“A”处样本稠密,代表性强,而样本“B”远离其他样本,很可能是个离群点,选出后对构建回归模型有害无利,反而不如只用最初选出的两个样本的效果.

图1 基于池的ALR 中样本的代表性与多样性[17]Fig.1 Illustration of representativeness and diversity in pool-based ALR[17]
3)多样性.所选样本应尽可能分散在整个输入空间中,而不是一个小的局部中,以便学习一个良好的全局模型.例如图1 中,绝大部分样本分布在3 个簇中,那么选择3 个样本时,应该从3 个簇中分别选出一个,让样本更加多样,而不是只从其中一个或两个簇中选.
多样性和代表性经常会有一定的冲突,所以应该折中平衡考虑.一个常用的方法是先对所有待选样本聚类,然后选取不同簇中靠近簇中心的样本,如下文中的RD 方法.
接下来,我们介绍3 种在文献中已有的基于池的无监督ALR 方法,并对照以上3 个标准对其进行检查.假设数据池由N个d维未标注样本xn=,n=1,2,···,N组成,用户将从中选择M个进行标注.
1.1 P-ALICE
Sugiyama 等[13]提出了一种基于泛化误差条件期望的重要性加权最小二乘方法(Pool-based active learning using the importance-weighted leastsquares learning based on conditional expectation of the generalization error,P-ALICE),这是一种无监督的ALR 算法,用于选择要标注的初始少量样本.其主要思想是识别M个样本及其相关权重,计算训练样本与测试样本之间的协变量偏移,由这M个样本构建的加权线性回归模型可以最小化N个样本上的均方损失估计值.
设
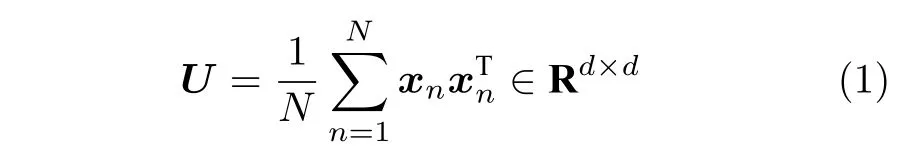
其中,U-1∈Rd×d是U的逆,表示U-1的第(i,j)个元素.P-ALICE 首先定义关于λ的重采样偏差函数

其中,λ∈[0,1],对于每个不同的λ,从样本池中选择M个未标注样本的概率与bλ(xn)成正比.将所选样本表示为,那么,在 N 个样本上的均方损失可以如下进行估计:

综上所述,对照ALR 的3 个标准,P-ALICE只考虑了信息性(均方损失估计值),没有考虑代表性和多样性.
1.2 GSx
Yu 等[16]提出了一种基于贪婪采样(Greedy sampling,GS)的ALR 算法.在给定一个初始未标注样本的情况下,GS 不需要任何标签信息就可以选择其他未标注的样本.但是,GS 初始至少需要一个确定的未标注样本,文中并没有对第1 个样本的选取进行解释.因此,Wu 等[18]提出了GSx 方法,将第1 个样本指定为最接近N个未标注样本中心的样本.接下来对GSx 算法进行介绍.

再选择具有最大dn的样本进行标注.重复此过程,直到选择的样本数量达到M.
综上所述,对照ALR 的3 个标准,GSx 仅考虑多样性,没有考虑信息性和代表性.
1.3 RD
Wu[17]提出了一种基于样本代表性(Representativeness)和多样性(Diversity)的方法,简称RD.
RD 主要由两部分组成:一部分是初始化(无监督过程),另一部分是后续迭代(有监督过程).RD的无监督过程首先对N个未标注样本进行k-means聚类(k=d+1),然后选择最接近每个聚类中心的样本进行标注.在文献[15]中也使用过类似的方法.
顾名思义,RD 在初始化时仅考虑代表性和多样性,没有考虑信息性.
1.4 小结
表1 中总结了P-ALICE、GSx 和RD 考虑的标准.可见,这3 种方法都只考虑了ALR 的3 个基本标准中的1 个或2 个.因此,仍有改进的空间.

表1 基于池的无监督ALR 方法中考虑的标准Table 1 Criteria considered in the three existing and the proposed unsupervised pool-based ALR approaches
2 IRD算法
本节对本文提出的基于池的无监督ALR 算法--IRD 进行介绍.顾名思义,IRD 同时考虑信息性、代表性和多样性.
设M为要选择的样本数量,d为特征维数.接下来分别讨论IRD 算法在3 种情形(M=d+1,M <d+1,以及M>d+1)下的实现.
2.1 情形1:M=d+1
对于d维特征数据,通常需要选择至少d+1 个样本来构造一个线性回归模型f(x)=xTw+b,其中w∈Rd×1为回归系数,b为偏置.接下来从d=2维的特殊样本开始,对IRD 的基本思想解释说明(图2).
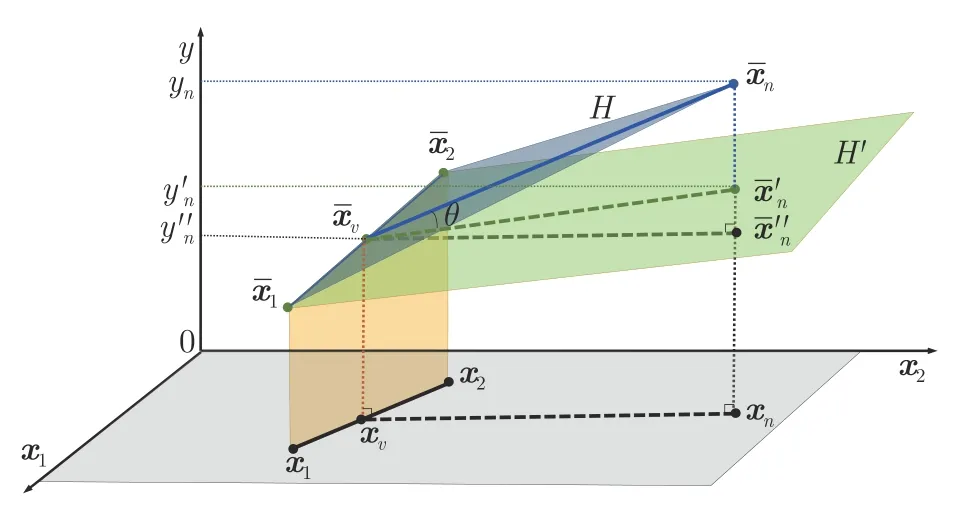
图2 当d=2 时IRD 算法图示Fig.2 Illustration of IRD whend=2
假设前两个未标注样本x1和x2已确定,现在需要选择第三个样本.为了便于说明,记=[xn;yn]∈R(d+1)×1,n=1,···,N.
假设H′为通过和的d维最佳流形,并且能够最佳地拟合其余的N-2 个样本.在无监督问题中,H′是未知的,但如果给定所有,并要求H′必须通过和,那么一定会存在这样的H′.

从图2 中,可以得到:

因此,基于以上推导和可以在基于池的无监督ALR 中使用的所有信息,可以近似得到:

式(10)从希望H和H′尽可能接近推导而来,因此这考虑了xn的信息性.此外,|xv-xn|也可以看作从xn到已确定样本(在这里也就是和)之间的距离.要使θ变小,则需要|xv-xn|尽可能大,即式(10)也保证了所选样本之间的多样性.综上所述,使用式(10)选择第3 个样本时同时考虑了信息性和多样性.
但是,如果仅使用式(10)作为选择第3 个样本的准则,它将始终选择距离最远的样本,那很有可能是一个离群点.为了同时考虑到代表性,可以计算从xn到N个样本的平均距离,结合到式(10)中,从而选择最佳的样本进行标注2我们还考虑了其他兼顾代表性、信息性和多样性的方法,例如=,但这种方法会引入超参数λ,并且我们的实验表明,从最佳的λ获得的性能要比式(11)差.因此,由于其简单性和准确性,我们最终使用式(11)作为选择准则.:
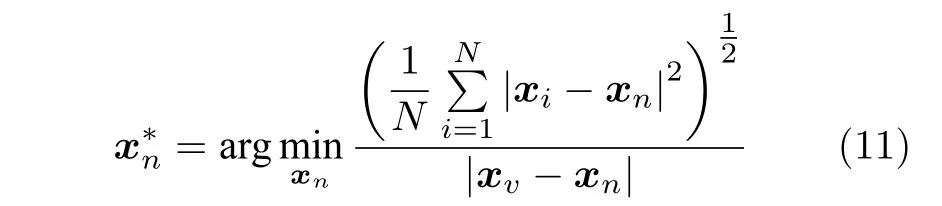
当d>2时,同理,可以用 (d-1)维流形C来代替,所有已确定的 d个样本都位于这个流形上.那么,可以将式(11)改写为

其中,dist(xn,C)表示从xn到流形C的距离.
为了计算 dist(xn,C),首先需要找到一个垂直于C的向量w∈Rd×1,即满足
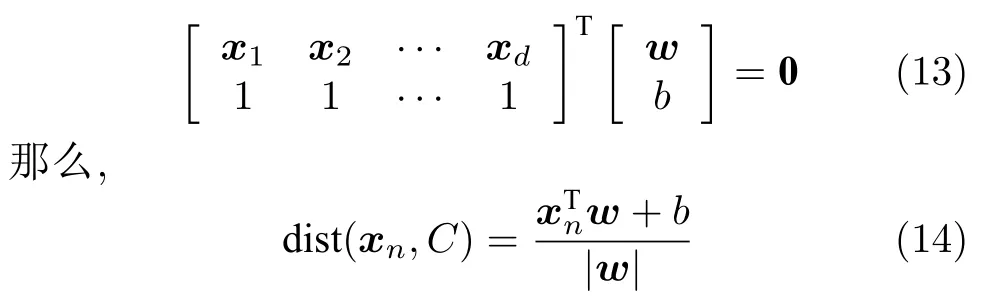
类似于式(12)的方法尚未出现在ALR 中.在用于分类的AL 方法中,有一些用于选择最接近当前分类边界的样本(即具有最大不确定性的样本)进行标注的方法[21-23],但是它们与式(12)有3 个显著区别:
1)式(12)适用于回归问题,而目前文献中的选择最接近当前分类边界样本的方法[21-23]都是针对分类问题的.
2)式(12)是完全无监督的,即只需要知道样本的特征信息而无需知道其输出.文献中针对分类问题的方法[21-23]都是有监督的,要求必须提供一些有标注的样本来初始化分类器,从而计算待选样本到分类界面的距离.
3)式(12)同时考虑了待选样本的信息性和多样性,而传统分类问题中的方法[21-23]只考虑信息性.
2.2 迭代改进
上述方法是在前d个样本确定的情况下,选择第 (d+1)个样本.第 (d+1)个样本的最优性还取决于前d个样本的最优性.
因此,本小节提出一种交替优化方法,以迭代方式优化第d+1 样本:首先通过GSx 或RD 算法确定前d个样本,再通过式(12)选择第 (d+1)个样本.然后反复固定d个样本,使用式(12)优化每个样本xt(t=1,···,d+1).重复此过程,直到选择的样本收敛或者达到最大迭代次数.
在M=d+1 情形下,IRD 的伪代码如算法1所示.

2.3 情形2:M <d+1
情形1 中考虑的是M=d+1,即所选样本数量刚好等于特征数加1,这是一种非常特殊的情况.实际上M可能小于d+1,在这种情况下,式(12)中的d-1 维流形C不能唯一确定,因此不能直接由式(12)得到.
对于这种情形,本小节提出一种新的处理方法:首先,对N个样本xn进行主成分分析(Principal component analysis,PCA),并确定前M-1 个主成分,然后将每个xn替换为其在M-1 个主成分方向的投影.则式(12)可以在转换后的xn上进行计算.
在M<d+1 情形下,IRD 的伪代码如算法2所示.


2.4 情形3:M >d+1
本小节考虑M>d+1 的情况.
首先,使用算法1 初始化d+1 个样本,然后继续确定另外的M-d-1 个样本:使用k-means 聚类 (k=M-d-1)在剩余的N-d-1 个样本中得到M-d-1 个簇,然后从每个簇中选择一个样本.这类似于RD 方法,但本文提出一种改进方法:不是直接选择最接近每个聚类中心的样本,而是使用迭代的方法来选择剩余的M-d-1 个样本.
不失一般性,假设前d+1 个样本已通过算法1 确定,接下来的M-d-2 个样本也暂时确定(例如最接近其簇中心的样本),要优化将从第(Md-1)个簇中选择的第M个样本.对于这个簇中的每个xn,将其与这个簇中其他样本的平均距离的倒数作为其代表性.记S为第 (M-d-1)个簇中样本的索引.则xn的代表性可以表示为

其中,|S|是S中元素的个数.
将xn到M-1 个已选样本的最小距离作为其多样性的度量,即

再结合代表性和多样性:

选择样本

来代替第M个样本.对每一个重复此过程,直到不再更新样本或达到最大迭代次数.
在M>d+1 情形下,IRD 的伪代码如算法3所示.


3 实验结果与分析
为了验证文中提出的基于池的无监督ALR 算法IRD 的有效性,在12 个数据集和3 种线性回归模型上进行了实验.本节将对实验结果进行分析讨论.
3.1 数据集
本文使用了12 个来自不同应用领域的数据集进行实验,其基本情况如表2 所示.

表2 12 个数据集的总结Table 2 Summary of the 12 regression datasets
其中9 个数据集来自UCI 机器学习数据库3http://archive.ics.uci.edu/ml/index.php,2个来自CMU StatLib Datasets Archive4http://lib.stat.cmu.edu/datasets/.这些数据集在其他的ALR 实验[7-8,16-18]中也用过.其中两个数据集(autoMPG 和CPS)同时包含数字型和类别型特征,因此首先使用one-hot 编码进行处理,将类别型特征转换为数字型特征,再进行ALR实验.
本文还使用了一个公开的情感计算数据集:VAM (Vera am Mittag)数据库[2],这个数据库也得到了广泛应用[20,24-27].它包含来自47 位讲话者的947条情感语音样本,从中提取了46 个声学特征[26-27],其中包括9 个音高特征、5 个持续时间特征、6 个能量特征和26 个MFCC 特征,对情感的3 个维度(愉悦度、唤醒度和优势度)进行预测.在本文实验中,只将唤醒度作为回归输出.
对于每个数据集,采用z-score 对输入的每一维进行标准化.
3.2 对比算法
本文将IRD (cmax=5)与以下4 种算法进行ghttp://archive.ics.uci.edu/ml/datasets/energy+efficiencyhhttps://dblp.uni-trier.de/db/conf/icmcs/icme2008.html
ihttps://archive.ics.uci.edu/ml/datasets/Concrete+Compressive+Strengthjhttps://archive.ics.uci.edu/ml/datasets/Airfoil+Self-Noisekhttps://archive.ics.uci.edu/ml/datasets/Wine+Quality比较:
1)随机采样(Random sampling,RS):随机选择M个样本进行标注.
2)P-ALICE:在第1.1 节中已经介绍.参数λ从 {0,0.1,0.2,0.3,0.4,0.41,0.42,···,0.59,0.6,0.7,0.8,0.9,1} 中选择最佳的一个.
3)GSx:在第1.2 节中已经介绍.
4)RD:在第1.3 节中已经介绍.
3.3 评价过程
对于每个数据集,每一次重复实验随机选择50%的样本作为样本池,其余50%作为测试集,每种算法从完全未标注的样本池中选择M∈[5,15] 个样本进行标注,然后建立线性回归模型.所有实验均重复100 次.
在测试集上进行预测,使用均方根误差(Root mean squared error,RMSE)和相关系数(Correlation coefficient,CC)作为性能评价指标.
对于每种方法,训练3 个不同的线性回归模型5对普通最小二乘法(Ordinary least squares,OLS)回归也进行了尝试,IRD 依然取得了最佳表现.但当训练样本较少时,OLS 非常不稳定,因此在实际中不是一个合理的选择,本文不讨论其结果.:
1)岭回归(Ridge regression,RR),L2 正则化系数λ=0.5.由于选择的样本数量很少,本文使用较大的λ以减小回归模型的方差.
2)LASSO,L1 正则化系数λ=0.5.
3)线性支持向量回归(Support vector regression,SVR),ϵ=0.1×std(y)(std(y)是M个选择样本真实标签的标准差),box constraintC=1.SVR 包含L2 正则项,其等效正则化系数为,与RR 和LASSO 中的大小相同.
在后面的小节中主要给出了RR 模型上的结果,因为它的RMSE 和CC 通常比LASSO 和线性SVR 更稳定,尤其对于RS 方法而言.但是,如第3.5节所示,当使用LASSO 或线性SVR 时,IRD 相对于其他算法(尤其是RS)的提升效果可能更大.
3.4 RR上的结果
图3 中展示了使用RR 作为回归模型,在12 个数据集上5 种采样方法的平均RMSE 和CC6由于页面限制,只展示了RR 的详细结果,因为它通常表现更稳定.其他两个回归模型上的结果类似..
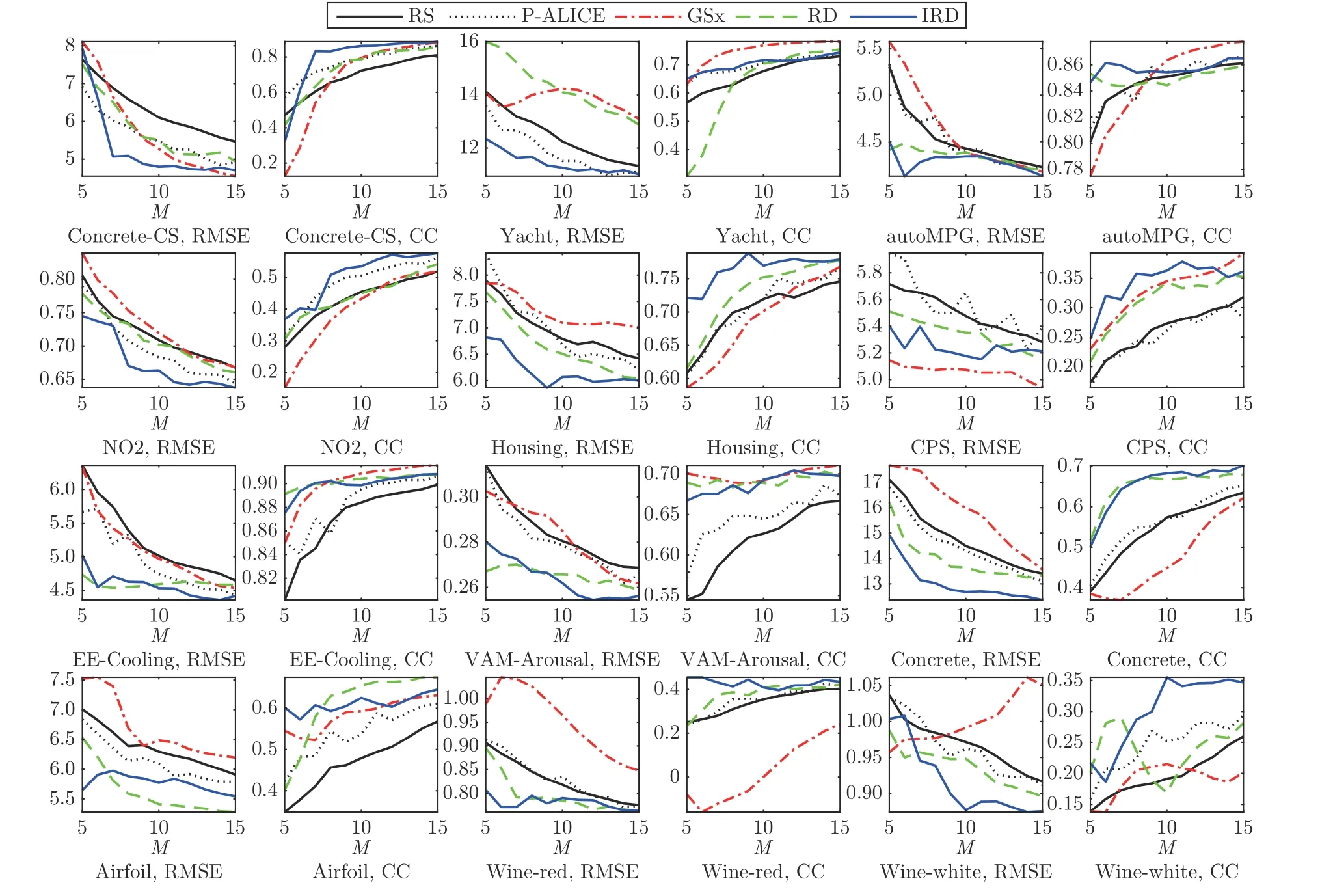
图3 12 个数据集上的平均RMSE 和CC (mRMSE 和mCC;重复运行100 次)(回归模型为RR (λ=0.5))Fig.3 Mean of the RMSEs and the CCs on the 12 datasets,averaged over 100 runs (RR (λ=0.5)was used as the regression model)
通常,随着M的增加,5 种采样方法的RMSE和CC 也会随之得到改善,因为有更多的训练样本加入回归训练,逐渐提升了回归性能.但仍然可能会存在一些波动,尤其是在样本数量较少的情况下.因为仅从少量标注样本中训练得到的线性回归模型可能存在很多随机性和不确定性.
在大多数数据集和大多数M取值上,RS 和GSx 具有更大的RMSE 和更小的CC,即它们的性能相对于另外3 种算法较差.IRD 在大多数数据集和大多数M取值上都取得了最小的RMSE 和最大的CC,表明IRD 是表现最佳的样本选择方法.
为了更全面地进行比较,我们还计算了100 次重复实验RMSE 和CC 平均值的曲线下面积(Area under curve,AUC),分别记为AUC-mRMSE 和AUC-mCC,结果如图4(a)所示.由于不同数据集上AUC 的大小差异很大,不便在一张图中展示,因此根据RS 的结果进行了归一化处理,使图4(a)中RS 的结果始终为1.图4(a)表明:

图4 12 个数据集上归一化AUC-mRMSE 和AUC-mCCFig.4 Normalized AUCs of the mean RMSEs and the mean CCs on the 12 datasets
1)IRD 在12 个数据集中的10 个上均获得了最小的RMSE,在其余两个数据集中排名第2.平均而言,IRD 取得了最小的RMSE.它在10 个数据集上也取得了最大的CC,在其余2 个数据集上排名第2 和第3.平均而言,IRD 也取得了最大的CC.
2)平均而言,RD 的性能略优于P-ALICE,两者均优于RS.
3)GSx 在7 个数据集上的RMSE 表现最差,在另外3 个数据集上排名倒数第二,平均而言,GSx 的RMSE 最差.它在6 个数据集中的CC 也是最低,因此其CC 平均值也最低.
因此,5 种算法的性能整体排名是:IRD>RD>P-ALICE>RS>GSx.
表3 中展示了3 个回归模型、5 种无监督采样方法在12 个数据集上的平均AUC 情况.当M较小时,GSx 表现较差的原因可能是其选择的样本大多是离群点,而离群点的负面影响超过了GSx 多样性的正面影响.IRD 同时考虑了信息性、代表性和多样性,因此表现最好.
除了准确性,算法的稳定性也很重要.实际情况中,如果多种算法具有相似的性能,通常首选变化较小,也就是更稳定的算法.表3 展示了运行100次的AUC-mRMSE 和AUC-mCC 在12 个数据集上的平均标准差(Standard deviation,std)提升结果.可以看到,IRD 在标准差上相对于RS 的提升最大,即它是最稳定的ALR 方法.

表3 AUC-mRMSE/sRMSE 和AUC-mCC/sCC 的提升百分比Table 3 Percentage improvements of the AUCs of the mean/std RMSEs and the mean/std CCs
对于不同的M,我们统计了P-ALICE、GSx、RD 和IRD 对应的RMSE (CC)相对于RS 的比率,重复100 次实验在12 个数据集上取平均,结果如图5 所示.可见,当M较小时,IRD 相对于其他4 种方法的提升很大,因为IRD 同时考虑了信息性、代表性和多样性.随着M的增加,IRD 的优越性逐渐下降,因为随着标注样本数量的增加,每个样本最优性的影响就会减小.
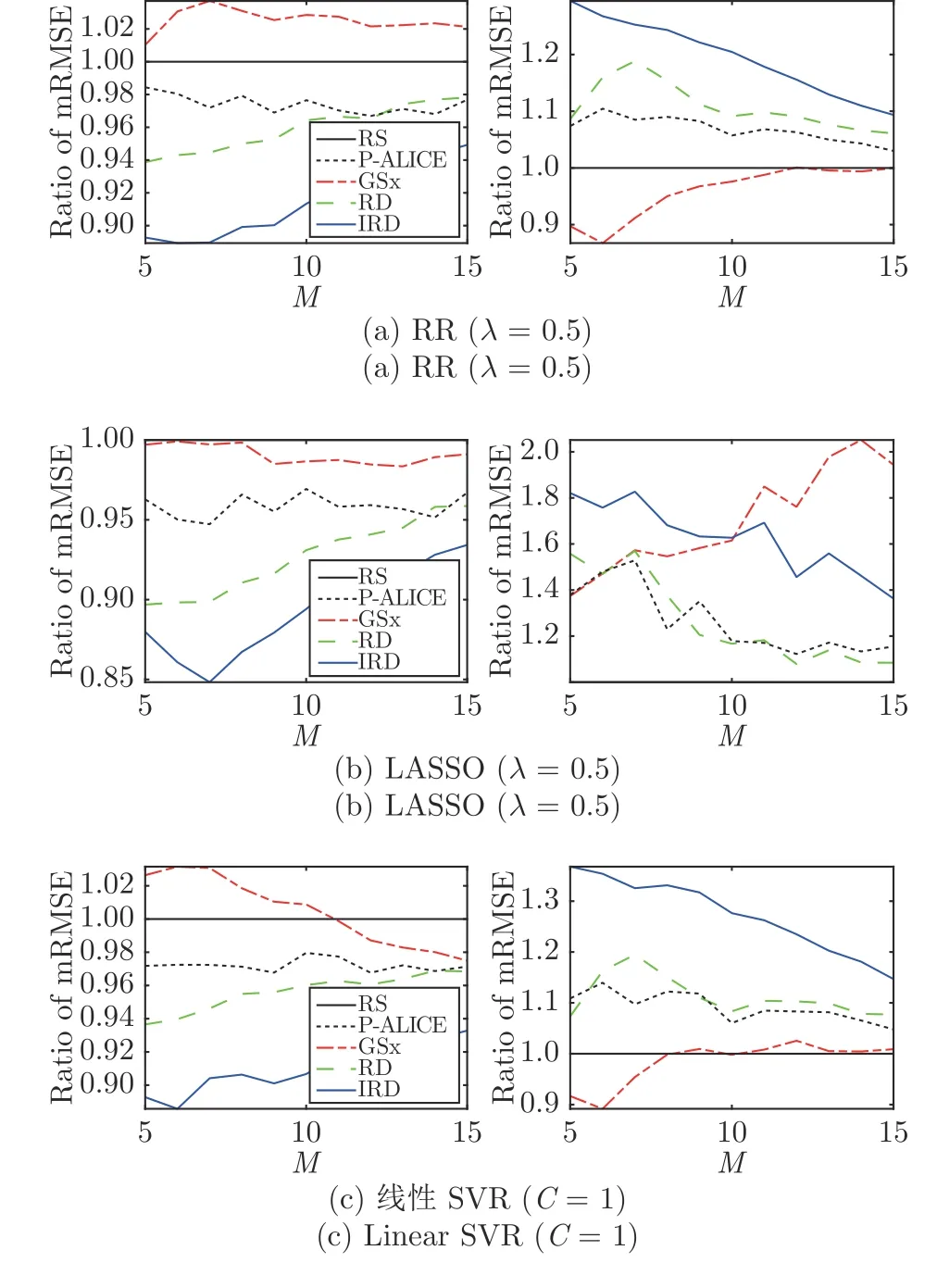
图5 对于不同的M,4 种ALR 方法的mRMSE 和mCC 相对于RS 在12 个数据集上的平均比率Fig.5 Ratios of the mean RMSEs and the mean CCs for differentM,averaged across 12 datasets
3.5 LASSO和线性SVR上的结果
当使用LASSO 和线性SVR 作为线性回归模型时,我们也重复了上述实验.结果如图4(b)和图4(c)所示.可以得到和图4(a)类似的结论,例如IRD 始终取得最佳的平均性能,而RD 则优于P-ALICE、RS 和GSx.此外,整体看来,相对于RR,4 种ALR算法(特别是IRD)在这两个模型上相对于RS 的性能提升更为明显.
为了量化4 种无监督ALR 算法相对于RS 的改善效果,我们也计算了其AUC-mRMSE 和AUC-m CC 的提升百分比,如表3 所示.无论使用哪种线性回归模型或性能指标,IRD 的平均表现都优于其他4 种方法.
3.6 统计分析
为了确定IRD 与其他4 种算法之间的性能差异是否具有统计意义,我们使用Dunn 检验[28]对几种方法的AUC-mRMSE 和AUC-mCC 在12 个数据集上的平均值进行了非参数多重比较检验,使用错误发现率(False discovery rate)方法[29]进行p值校正.结果如表4 所示,其中具有统计意义的结果以粗体标出.

表4 非参数多重检验的p值(α=0.05 ;如果p <α/2 拒绝H0).Table 4 p-values of non-parametric multiple comparisons (α=0.05 ;rejectH0ifp<α/2)
结果表明,无论使用哪种线性回归模型,IRD的RMSE 和CC 相对于RS、P-ALICE 和GSx 的提升始终具有统计学意义;相对于RD,CC 的提升具有统计学意义;使用线性SVR 时,RMSE 的提升也具有统计学意义.
3.7 选择样本的可视化
为了更直观地了解不同ALR 算法选择样本之间的差异,我们在一个典型数据集(Housing)上使用t-SNE[30]将样本映射到2 维空间.图6 展示了3个不同的M值对应的4 种ALR 算法选择的样本.P-ALICE 的样本权重在绘图中没有显示.
图6 中,GSx 倾向于选择位于边界的样本,这样的样本很有可能是离群点,且所选样本的分布情况与池中的样本不一致.因此,它的平均性能在4种算法中是最差的.与GSx 相比,P-ALICE 和RD选择的样本在池中分布更均匀.IRD 选择的样本倾向于靠近池的边界,但不完全位于边界,这样的样本不太可能是异常点,并且选择的样本的分布情况与池中样本更一致.这些都可能是IRD 表现较好的原因.

图6 在Housing 数据集上不同ALR 算法所选样本(星号)的t-SNE 可视化Fig.6 t-SNE visualization of the selected samples(asterisks)from different ALR approaches on Housing dataset
3.8 cmax对IRD的影响
算法1~3 中有一个重要参数:cmax,即最大迭代次数.当cmax=0 时,IRD 等效于RD.本小节通过设置cmax>0 来探究IRD 的性能是否优于RD.
图7 展示了在3 种线性回归模型上,cmax∈[0,10]的归一化AUC (相对于RS)的变化趋势,这是在12 个数据集上重复100 次 实验的平均结果.如图所示,IRD 的性能随着cmax的增加而迅速提升,并且总是在cmax=5 之前就达到了最优,这意味着IRD 是一种既有效又高效的算法.

图7 对于不同的cmax,4 种ALR 算法的AUC-mRMSE和AUC-mCC 相对于RS 在12 个数据集上的平均比率Fig.7 Ratios of AUCs of the mean RMSEs and the mean CCs for differentcmax,averaged across 12 datasets
3.9 λ对IRD的影响
为了研究5 种无监督采样方法的性能对3 个线性回归模型正则化系数的敏感性,我们对λ ∈{0.01,0.05,0.1,0.5,1}进行了重复实验.线性SVR有一个等价的L2 正则化系数,等效设置为C ∈{50,10,5,1,0.5}.将每种采样方法在不同参数回归模型下的AUC 结果相对于RS (λ=0.5)进行归一化,如图8 所示.
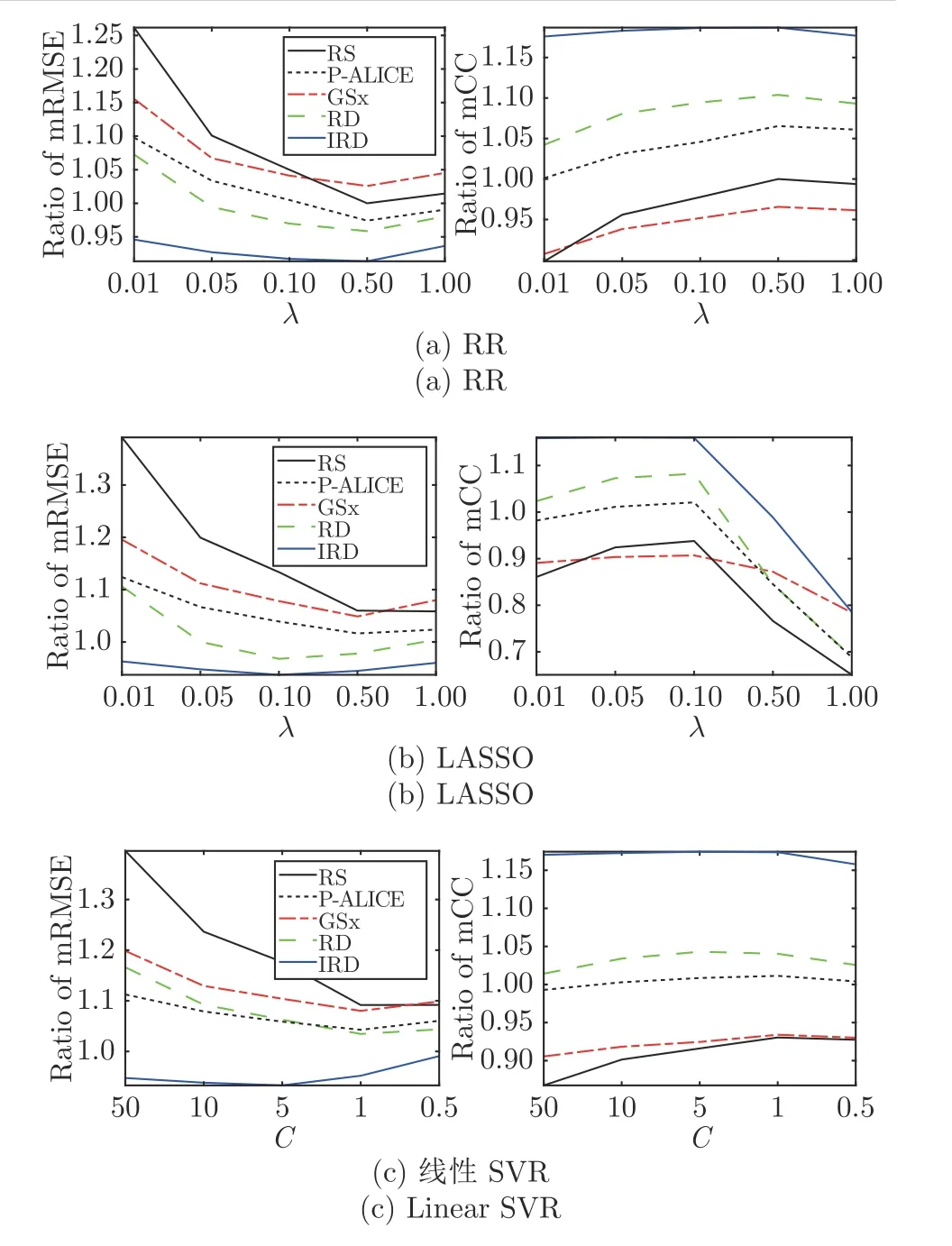
图8 对于不同的λ(RR 和LASSO)和C(线性SVR),4 种ALR 算法的AUC-mRMSE 和AUC-mCC 相对于RS 在12 个数据集上的平均比率Fig.8 Ratios of the AUCs of the mean RMSEs and the mean CCs,averaged across 12 datasets,for differentλ(RR and LASSO)andC(linear SVR)
整体来看,5 种无监督采样方法的性能首先随着λ的增大而提高,然后下降.然而,无论λ(C)取值为多少,IRD 的表现通常都是最好的,RD 次优.当λ较小时,IRD 相对于其他4 种方法的提升更大.此外,可以看出IRD 对参数λ不是很敏感,这将有利于实际应用.
3.10 三个标准的影响
为了研究信息性、代表性和多样性分别对IRD的影响,我们将IRD 与三个变体进行比较:
1)IRD (cmax=5):本文提出的方法,在第2节中已介绍.
2)ID:当M=d+1 时,只考虑式(12)的分母部分;当M>d+1 时,只考虑式(17)中的D(xn).即只考虑信息性和代表性.
3)RD:等同于cmax=0 时使用RD 进行初始化的IRD.即只考虑代表性和多样性.
对于M∈[5,15],每种方法在12 个数据集上运行100 次,训练3 种线性回归模型:RR (λ=0.5)、LASSO (λ=0.5)和线性SVR (C=1).图9 展示了对于不同的M取值,IRD 及变体的RMSE 和CC 相对于RS 的平均比率.3 个回归模型上的结论是类似的.通常,3 种ALR 方法都优于RS.IRD 仍然表现最好,这表明同时考虑信息性、代表性和多样性至关重要.

图9 对于不同的M,IRD 及其变体的mRMSE 和mCC相对于RS 在12 个数据集上的平均比率Fig.9 Ratios of the mean RMSEs and the mean CCs w.r.t.differentM,averaged across 12 datasets
4 结论
主动学习通过选择最有价值的样本进行标注,从而利用较少的训练数据就可以建立较好的机器学习模型.这在许多实际应用中有着重要的作用,因为数据的标注过程往往需要耗费大量的时间和经济成本.大多数现有的主动学习方法是有监督的:能够从少量的标注样本中建立一个初始的模型,基于模型查询新的数据,然后进行迭代更新.本文考虑了线性回归中完全无监督的基于池的主动学习问题,即在完全不知道任何标签信息的情况下,最优地选择初始的少量样本进行标注.文中提出一种新的主动学习算法IRD,该算法同时考虑了主动学习中的3 个重要标准:信息性、代表性和多样性.在来自于不同应用领域的12 个数据集和3 种不同的线性回归模型(RR、LASSO 和线性SVR)上进行了大量实验,充分验证了本文提出方法的有效性.
——勉冲·罗布斯达

