通信延时环境下异质网联车辆队列非线性纵向控制
李永福 何昌鹏 朱 浩 郑太雄
道路交通运输是国民经济的血脉,但现有道路基础设施难以扩展,由于道路通行能力不足和汽车保有量迅速增加而引起的交通拥堵、尾气污染等问题使交管部门面临严峻的挑战.随着自动驾驶技术和V2V (Vehicle-to-vehicle)通信技术的迅猛发展,传统的自适应巡航控制ACC (Adaptive cruise control,ACC)逐渐发展成为协同自适应巡航控制 (Cooperative adaptive cruise control,CACC).它利用V2V 通信技术共享车辆状态(位置、速度、加速度)信息,提升了车辆队列的稳定性并降低了反应延迟[1].研究表明,车辆以队列模式行驶可有效提高道路通行效率、车辆燃油经济性和行驶安全性[2-3].因此,从改善车辆行驶模式的角度研究车辆队列系统的控制方法,以提高道路通行效率和车辆燃油利用率,具有巨大的应用价值和研究意义.
车辆队列控制的目标是使队列中车辆保持等间距匀速行驶,且要求相邻两车不能发生碰撞[4].然而通信拓扑结构的改变以及通信延时或丢包的存在可能导致队列中车辆速度振荡,从而引起队列不稳定.诸多学者针对这一问题开展了广泛研究[5-12].文献[5]针对Ad-hoc 型车辆网络的容量限制和Bernoulli随机丢包问题,提出了一种车辆编队算法,解决了网络冲突并保证了车辆队列的弦稳定性.考虑输入延时和前车间距,文献[6]提出一种仅依靠车载传感器感知信息的车辆队列控制器,并得出了延时边界和弦稳定性条件.利用矩阵特征值分析方法,文献[7]针对多种通信拓扑结构对车辆队列稳定性和扩展性进行分析,得到了其稳定条件.针对通信拓扑切换问题,文献[8]提出一种考虑有限时间稳定的非线性车辆队列控制器,实现了固定通信拓扑和切换通信拓扑下的车辆队列控制.通过引入Markov模型描述网络的随机接入过程,文献[9]提出一种适应信道衰落条件下的车辆队列控制算法.文献[10]充分讨论了通信延时对几种主要车辆队列控制方法的影响,结论表明领导车辆与跟随车辆状态信息的传递结构决定了车辆队列的弦稳定性,而与车辆动力学和控制器设计无关.文献[11]考虑动力传动系统延时并引入事件驱动机制提出一种适用于Adhoc 网联车辆队列的反馈控制器.考虑IEEE 802.11P 协议真实环境下的通信延时,文献[12]基于一致性协议提出一种车辆队列控制方法,其分析和实验结果表明领导车辆信息的全局可达对于车辆队列的稳定性至关重要.文献[13]考虑领导车辆的加速度扰动和风阻,提出基于一种分层混合模型的鲁棒延时车辆队列控制器,并保证了车辆队列的弦稳定性.然而,由于未考虑行车安全,基于上述研究的车辆队列控制可能导致相邻车辆间出现碰撞问题.
从车辆队列的匀质/异质性角度来看,许多与车辆队列控制有关的研究均假设车辆队列为匀质队列.针对匀质车辆队列的协同控制问题,文献[14]利用网联环境下队列中的一致性和队列间的群一致性,提出一种新的匀质车辆多队列协同控制器.文献[15]基于分层模糊逻辑,提出了一种融合滑模控制和模糊控制的双层变结构控制方法.事实上匀质车辆队列的假设过于理想化,因为真实交通场景中车辆通常是异质的,因此部分学者对异质车辆队列展开了研究.考虑车辆动力学因素,文献[16] 提出一种三阶异质车辆队列协同控制器,并引入了基于代数黎卡提方程的综合分析方法,得到了控制增益的稳定性区域.针对智能车辆传感器失效和采样周期影响的问题,文献[17]提出一种适应切换延时系统的异质车辆队列控制方法,保证了队列行驶的一致性.文献[18]基于事件驱动机制提出满足通信资源有效性和弦稳定性的异质车辆队列控制方法.针对参数不确定性问题,文献[19]基于反步法提出一种车辆队列控制策略,同时满足队列的内部稳定和弦稳定.利用车辆的异质特性使队列控制更加符合实际,但交通流中车辆间的非线性相互作用的影响并未在控制器中考虑.
随着车辆队列控制理论的逐步发展,车辆碰撞风险的研究引起了学者的关注[20-22].文献[20]分析得出避免发生碰撞时车辆队列控制器设计应满足的四个条件,并具体给出了几种控制因素影响下的控制器设计方法.考虑车辆制动场景,文献[21]提出一种积分滑模控制器,保证车辆队列行驶过程中避免发生碰撞.文献[22]基于二阶积分模型,提出一种非线性车辆队列控制器,避免了车辆间的碰撞.然而,上述文献并未对车辆动力学的异质特性和交通流中车辆跟驰行为对车辆队列控制的影响进行全面地描述.
本文旨在研究通信延时环境下的车辆队列协同控制方法.考虑通信延时和车辆异质特性,基于车辆动力学模型,提出一种新的车辆队列非线性控制器,并深入分析通信延时对车辆队列稳定性的影响.本文的主要创新点包括:1)与现有文献[6-7,9-14,16-20]中设计的车辆队列线性控制器不同,本文提出一种基于车辆三阶动力学模型的非线性队列控制器;2)本文所设计的队列控制器,考虑了车辆间的跟驰作用关系,避免出现负的车辆间距和不合理的加/减速度,提高行车安全和舒适度,保证车辆的运动行为符合交通流理论;3)考虑了异质通信延时和异质车辆特性对车辆队列控制的影响,并利用Lyapunov-Krasovskii 定理分析得出了通信延时上界,保证了队列行驶的稳定性.
本文结构如下:第1 节为问题描述及模型建立,描述了车辆队列控制问题和通信拓扑结构表征并建立了车辆动力学模型;第2 节设计了考虑异质通信延时的非线性异质车辆队列协同控制器,并进行了稳定性和通信延时上界分析;第3 节进行了不同通信拓扑结构和有/无通信延时情形下的对比数值仿真验证和分析;第4 节进行总结.
1 问题描述及模型建立
1.1 问题描述
如图1 所示交通场景,考虑N+1 辆车组成的异质车辆队列,领导车辆编号i=0,跟随车辆编号i=1,2,···,N,车身长度用l表示.通过V2V 通信技术,队列中的车辆能够相互交换状态信息(位置p,速度v,加速度a),也可以通过激光雷达等距离传感器获取与前车的间距d.车辆的通信拓扑结构采用代数图论进行描述.将队列中跟随车间的通信拓扑抽象为一个连通图G(V,E,A),其中V={1,···,N}为图G中节点的集合,E⊆V ×V表示图G中两两节点的边集,即跟随车辆间的通信连接.A=[aij]N×N为连接矩阵,aij=1 表示车辆i与车辆j有通信连接,aij=0 表表示车辆i与车辆j未建立通信连接.Ψ=[ρ10,···,ρN0]T为跟随者车辆与领导车辆的连接矩阵,即与领导车辆的通信连接,ρi0=1表示i车与领导车辆建立通信连接,ρi0=0表示i车与领导车辆未建立通信连接.典型的前车-领导跟随式(Predecessor-leader following type,PLF)和双前车跟随式(Two-predecessor follwing type,TPF)通信拓扑结构如图2 所示.
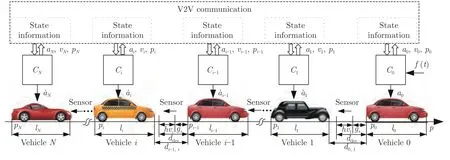
图1 车辆队列Fig.1 Vehicle platoon
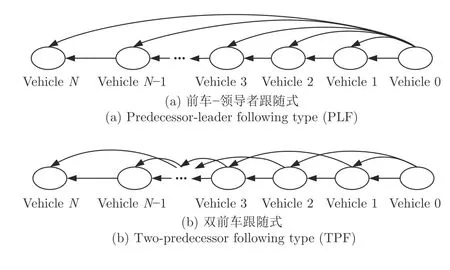
图2 通信拓扑结构Fig.2 Communication topology
1.2 车辆模型建立
根据文献[23],可建立车辆动力学模型
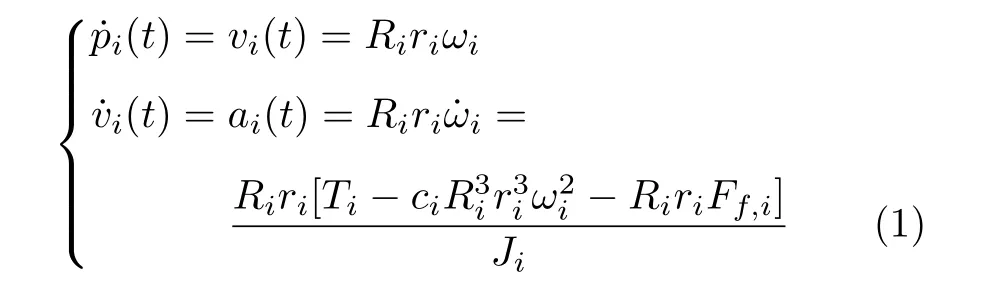
其中,ri是轮胎半径,Ri是齿轮比,ωi是引擎转速,Ti为引擎转矩,ci为空气阻尼系数,Ff,i表示摩擦阻力,Ji为引擎转动惯量.
考虑车辆传动系统的迟滞特性,建立一阶模型
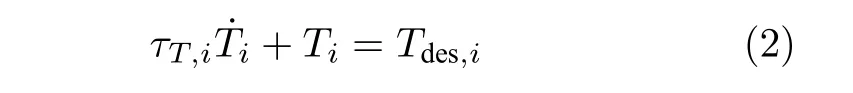
式中,τT,i为车辆动力传动系统的时间常数,Tdes,i为期望输出力矩.
为了简化计算,设计线性反馈控制律
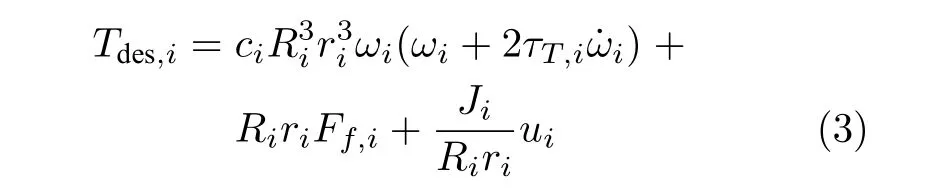
式中,ui为车辆的控制输入.
由上述反馈线性化策略,可得到三阶车辆动力学模型
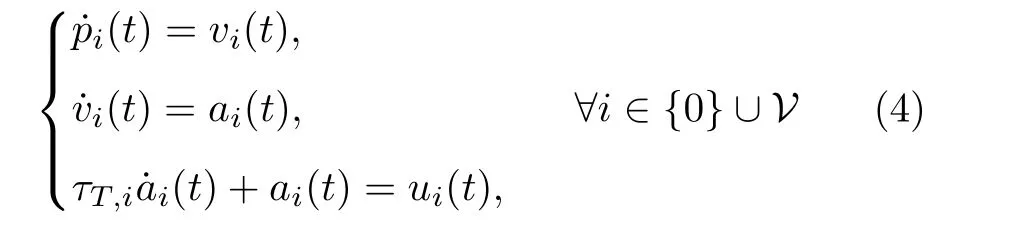
式中,pi(t),vi(t),ai(t)分别表示车辆i的位置,速度和加速度.ui(t)表示车辆i的控制输入,τT,i刻画了动力传动系统的惯性时间,不同类型的车辆具有不同的惯性时间,其刻画了车辆动力学的异质特性.
1.3 预备知识
引理 1[24].设三阶系统的特征多项式为

其中,z1,z2,z3为复数,则系统矩阵Hurwitz 稳定的必要条件为特征多项式(5)各项系数构成的主行列式的各阶主子式D1,D2,D3为正.
定义 1.集合C([a,b],Rn)是一个将区间[a,b]映射到 Rn的连续函数集合,对于函数φ ∈C([a,b],Rn)),定义连续范数‖·‖c:
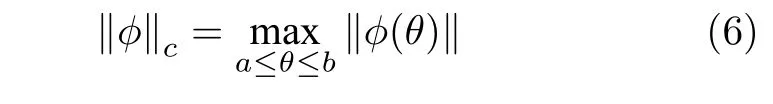
其中,向量范数‖·‖代表‖·‖2范数.
令C([-δ,0],Rn)为定义在 [-δ,0] 上的连续函数的Banach 空间,φ∈C([-δ,0],Rn),那么有‖φ‖c=max-δ≤θ≤0‖φ(θ)‖.
考虑如下延时微分方程
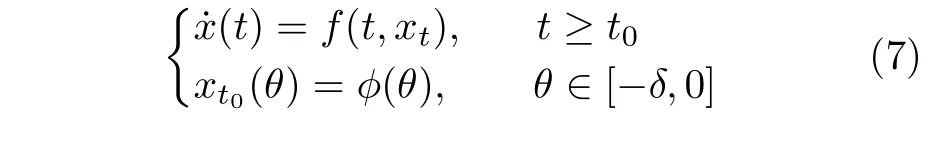
其中,δ>0,φ是初始条件的泛函,对于给定的t ≥t0,xt(·)表示将区间 [t-δ,t] 映射到 [-δ,0],也就是xt(θ)=x(t+θ),∀θ ∈[-δ,0].
引理 2[25].假设f:R×C([-δ,0],Rn)→Rn是一个 R×(C中的有界集)到 Rn中有界集的映射,并且u(s),v(s),w(s)是连续非减非负函数,此外对于s/=0,u(s)和v(s)取正值,且u(0)=v(0)=0.如果存在连续可微泛函V:R×C →R,
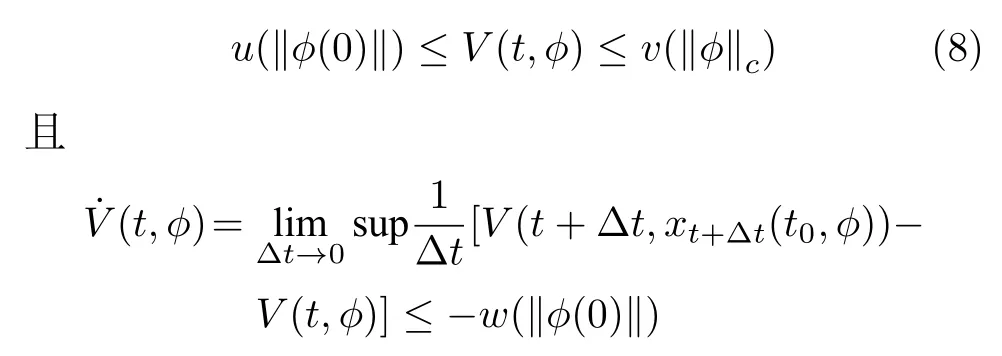
那么解x=0 是一致稳定的.
此外,如果对于s>0,w(s)>0,那么系统是一致渐近稳定的.如果
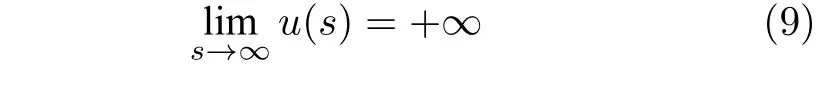
那么系统是全局一致渐近稳定的.
1.4 控制目标
车辆队列控制旨在使队列中所有车辆保持相同的速度和期望间距行驶,可以表示为

式中,l表示车身长度,gs是相邻两车的安全距离.
假设领导车辆匀速运动(领导车辆的加速度视为扰动),由此,可定义车辆位置、速度、加速度误差为
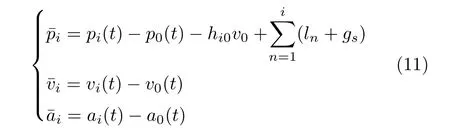
根据式(11),车辆队列控制目标可改写为
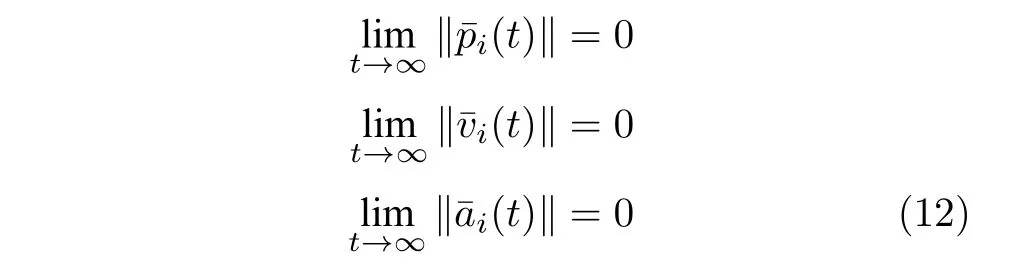
式中,(t),(t),(t)分别表示车辆i的位置、速度、加速度误差.
2 控制器设计与稳定性分析
2.1 控制器设计
针对上述车辆队列控制问题,考虑车身长度的异质性、车辆位置一致性、速度一致性以及车辆跟驰行为特性,设计分布式控制器:

在式(13)中,ki,w>0,ki,p>0,ki,v>0,k0,p>0,k0,v>0是反馈控制增益.aij∈{0,1}和ρi0∈{0,1}分别是跟随车辆i与车辆j,跟随车辆i与领导车辆之间的通信连接.hij和hi0分别是跟随车辆i与车辆j,跟随车辆i与领导车辆之间的间距常数.ln是第n(n=1,···,i)辆车的长度.gs是相邻车辆的安全距离.τij(t)与τi0(t)分别为跟随车辆i与车辆j,跟随车辆i与领导车辆之间的通信延时.车辆跟驰行为采用最优速度进行刻画[26]:

2.2 稳定性分析
针对通过V2X 通信获取其他车辆状态信息存在通信延时的情况,本文设计了考虑存在通信延时的控制器(13).可将该车辆队列系统视为一个延时系统,其稳定性可采用引理2 (Lyapunov-Krasovskii 定理)描述的延时系统稳定性证明方法,构造Lyapunov-Krasovskii 泛函加以证明,其详细证明过程如下.首先根据状态方程(4)和误差定义(11),跟随车辆与领导车辆间的距离时间常数关系hi0-hj0=hij=-hji,可得误差状态方程:

基于式(14),利用泰勒公式线性化可得
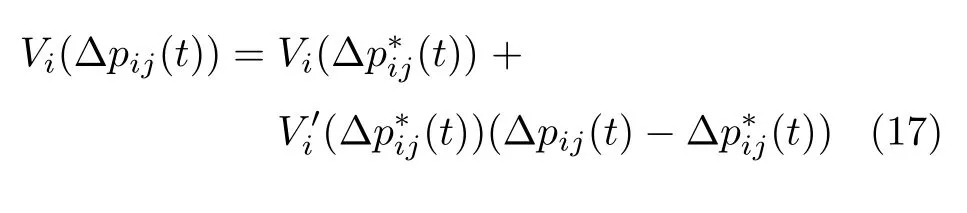

注 2.此部分内容主要为误差状态方程的线性化.由于考虑车辆跟驰行为特性,在控制器中引入了非线性项(14),为此,根据误差定义(11)变换状态方程(4)为误差状态方程(15),并采用泰勒公式获得线性化的误差状态方程(19),从而简化后续稳定性分析过程.

根据上述定义,车辆队列系统的误差状态空间表达式可以用以下延时微分方程表示为
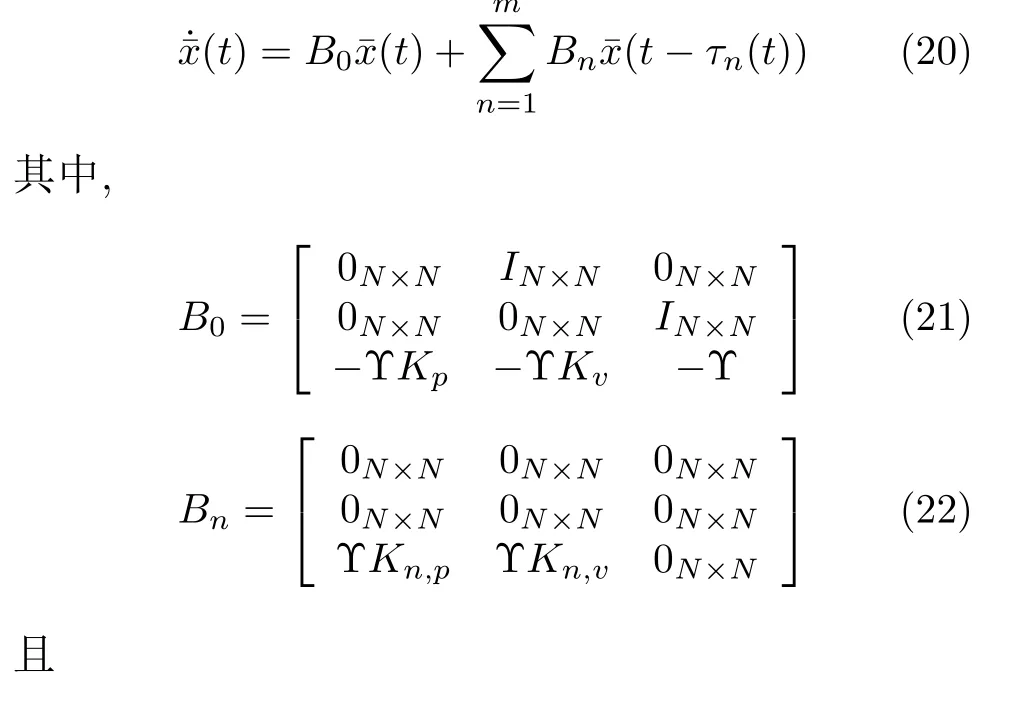
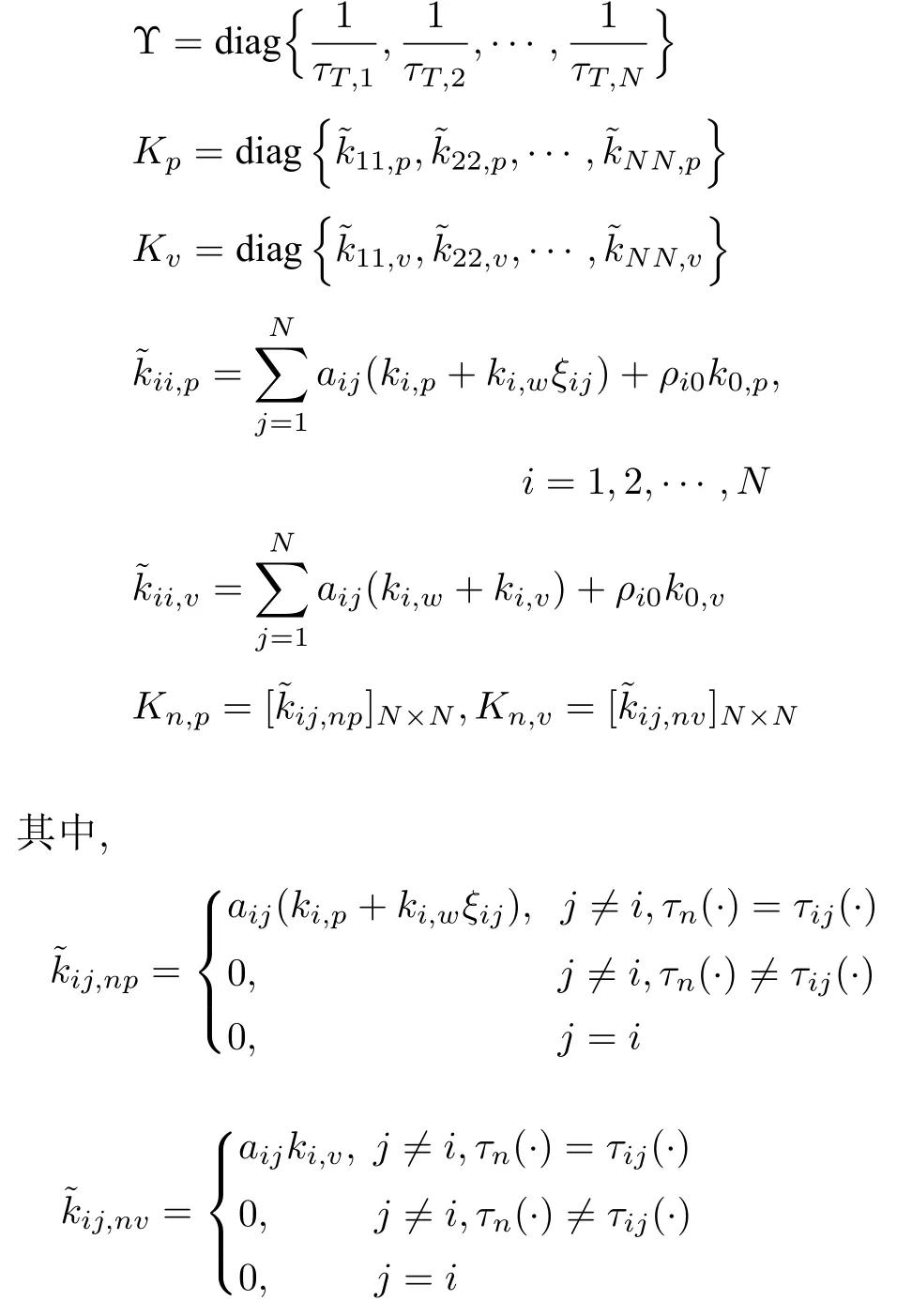
根据牛顿-莱布尼兹公式可得

因此,将式(20)代入式(23),可得
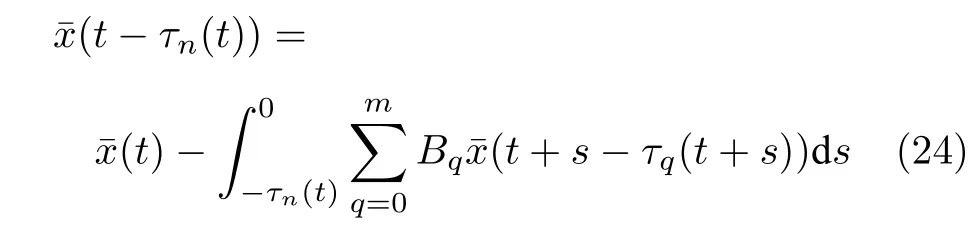
式中,B0,···,Bm由式(21)和式(22)表示,且τ0(t)≡0.
将式(24)代入时变系统(20)可以得到
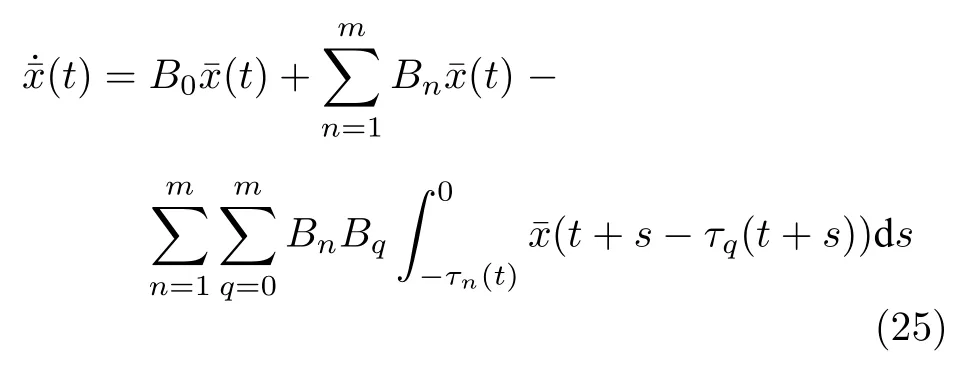
根据式(21)和式(22),可以得到BnBq=0,n=1,···,m,q=1,···,m(q/=0).因此系统(19)可以定义为
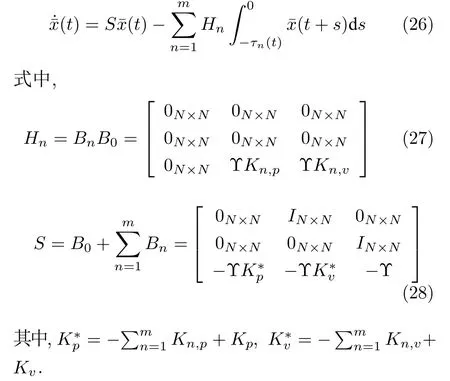
注 3.此部分内容主要为误差状态方程的积分变换.利用牛顿-莱布尼兹公式,对误差状态方程(20)做积分变换得到式(26),为利用Hadamard 不等式缩放Lyapunov-Krasovskii 泛函,分析系统稳定性.
定理1.考虑延时系统(26),设置控制参数ki,w,ki,p和ki,v为正.假设延时τn(t)(n=1,···,m)是有界的,即τn(t)∈[0,τmax],(t)∈(-∞,rn](∀t∀n)且rn≤1.那么存在常数τ*>0,对于τn(t)<τ*,∀n∀t有

当且仅当矩阵S是Hurwitz 稳定.
证明.(充分性):考虑系统(26)的Lyapunov-Krasovskii 泛函:

其中,选取矩阵P=PT>0且Mn>0(n=1,···,m),并定义如下连续非减的正值函数:
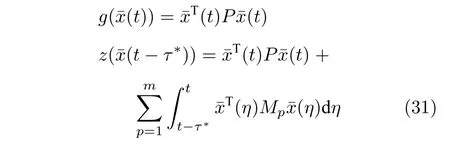
其中,τ*是可能的最大延时.
根据式(30)和式(31),引理2 的条件(8)可以满足,即

对式(30)求导可得
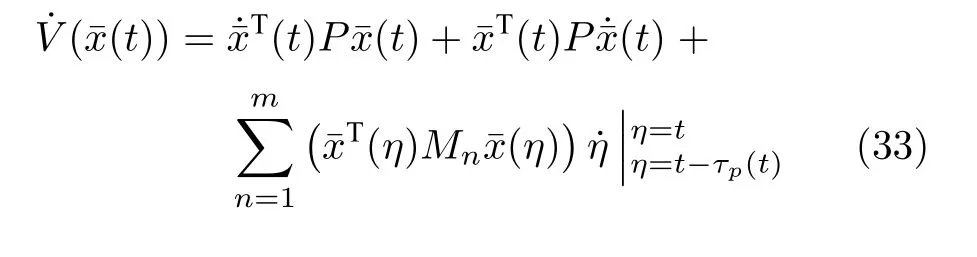
将式(26)代入式(33),可得

根据附录A,设置参数ki,w,ki,p和ki,v,使得矩阵S是Hurwitz 稳定的.且根据Lyapunov 理论,令STP+PS=-Q,其中,P,Q是正定的,P=PT.
对于任意的正定矩阵 Ξ,有[27]
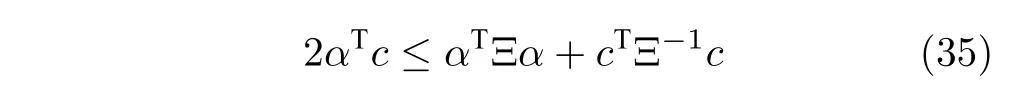
因此,令αT=TSHn,c=(t+s),Ξ=S-1,那么

根据式(36),式(34)可以改写为
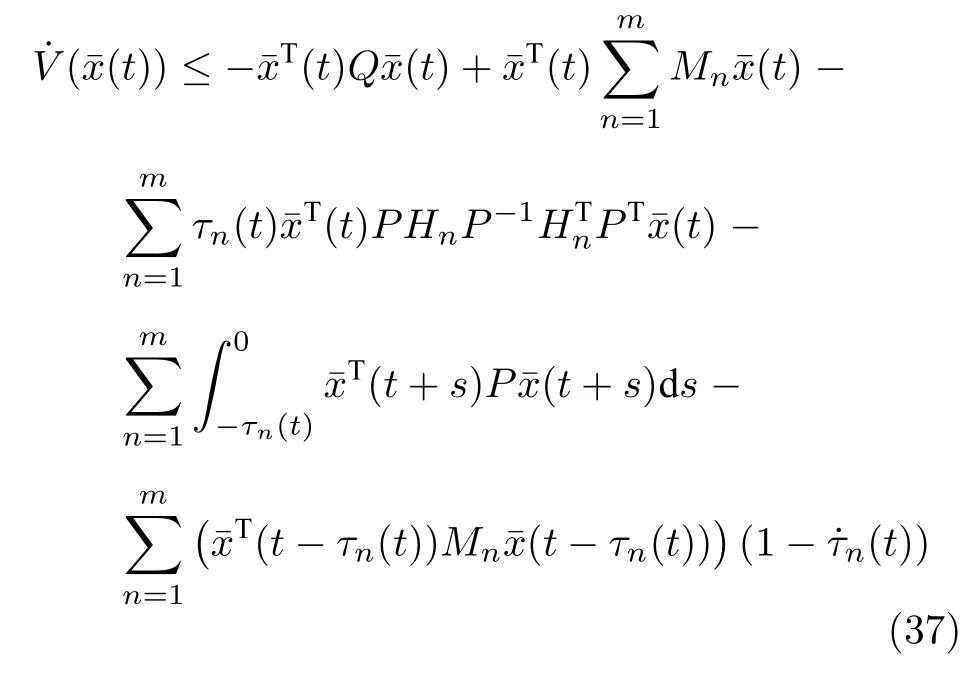
根据Hadamard 不等式[28],有
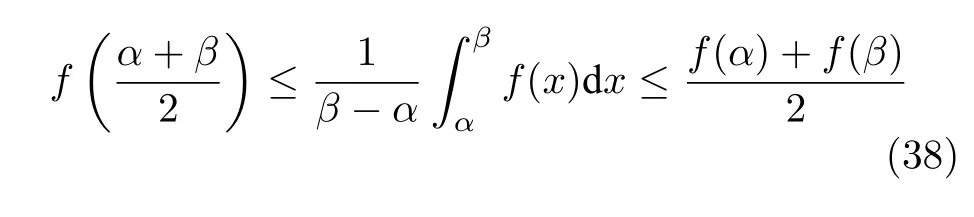
可以将式(37)的积分部分进一步缩放,以及代入延时边界可得
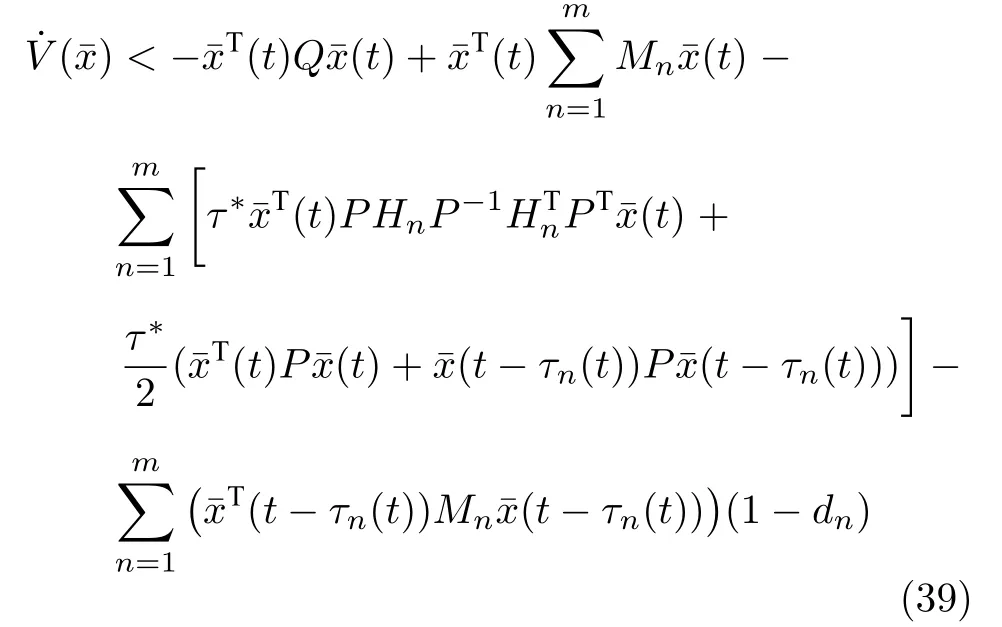
定义一个新的误差状态向量ε(t)=[(t),x¯(tτ1)(t-τm(t))]T,将式(39)重写为一个更简洁的形式

根据引理2 可得,保证延时系统一致渐近稳定的充分条件为 Λ 负定.由于rn≤1,∀n=1,···,m,因此n=2,···,m时 Λn负定.因此,当 Λ1负定时,Λ是负定的.即

注 4.此部分内容主要为基于引理2 的系统稳定性分析.基于引理2,通过构造Lyapunov-Krasovskii 泛函(30),且满足引理1 的条件(8),进一步根据Lyapunov 理论和Hadamard 不等式得到系统的延时上界条件.
2.3 弦稳定性分析
定义2.如果车辆队列系统中相邻两车的间距误差有如下关系:
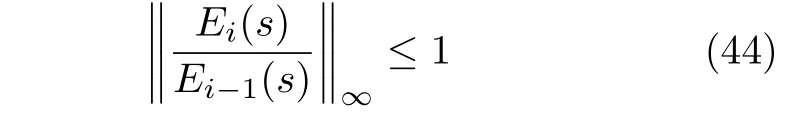
其中,Ei(s)是i车与i-1 车的间距误差,则称车辆队列系统满足弦稳定性(String stability)[29].
将车辆动力学模型(4)和控制器(13)进行拉普拉斯变换,同时考虑最差情形(通信延时最大),即选取τ*作为系统的通信延时,经过分析可得
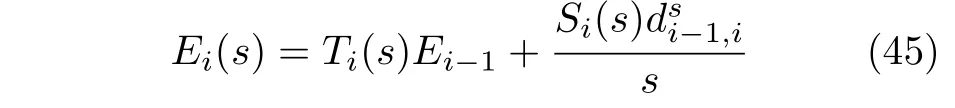
其中,Ti(s)和Si(s)的表达式及详细推导过程见附录B,控制增益的选取满足Ti(jω)<1.
3 仿真验证
本节将所提控制器(13)与文献[16]控制器分别在PLF 和TPF 通信拓扑结构且考虑无通信延时和存在最大0.03 s 延时情况下进行对比仿真实验,验证了所提控制器的有效性和通信时延情况下的优越性.首先选取N=8 辆车(1 辆领导车辆和7 辆跟随车辆)作为实验对象.车辆长度选取为一般的乘用车长度li=4+lrm,其中,lr∈[0,1].在保证无碰撞风险的情形下,领导车辆的初始位置设定为p0(0)=150m,跟随车辆的初始位置p(0)=[126,105,83,64,43,22,1]m.领导车辆的速度如式(46)所示:
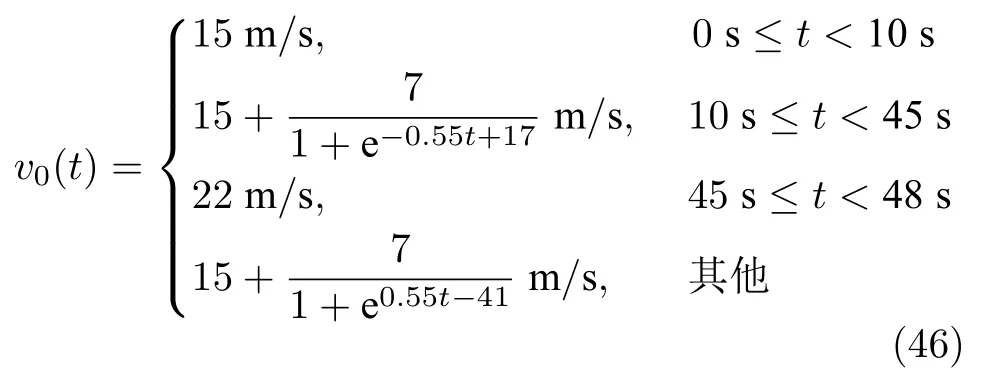
跟随车辆的初始速度和加速度分别为vi(0)=v0(0)m/s,ai(0)=0 m/s2,i=1,2,···,N.时变延时 0<τ(t)<τ*=10.32×10-2s,其中,τ*大于典型的IEEE802.11p 车联网通信延时[30].控制器参数及车辆结构参数如表1 所示.

表1 控制器参数Table 1 Controller parameters
3.1 PLF通信拓扑结构下的仿真分析
领导车辆按照式(46)所给速度行驶,跟随车辆初始时刻速度与领导车辆相同,在无通信延时和最大0.03 s 延时情况下,文献[16]的控制器和本文所提控制器(13)作用下的位置、速度、加速度和间距误差轨迹如图3~6 所示,所有仿真图中的v0,v1,···,v7分别表示Vehicle 0,Vehicle 1,···,Vehicle 7.图3 为车辆的位置轨迹.由图3(a)以及图3(b)~3(d)得出,在有/无通信延时和文献[16]的控制器及本文所提控制器(13)的作用下,队列内的所有车辆能够保持稳定的间距行驶,并在领导车辆加速和减速后队列仍能保持稳定和期望的安全间距.

图3 PLF 拓扑下车辆队列的位置图Fig.3 Position profile for a platoon under PLF topology
图4 是队列内所有车辆的速度图.基于图4,领导者具有时变速度,可以分为3 个阶段:加速、匀速和减速.在文献[16] 的控制器及本文所提控制器(13)作用下,跟随车辆的速度最终可收敛到与领导车辆速度一致.图4(b)和4(d)表明存在通信延时情况时,文献[16] 的控制器由于未考虑通信延时的间距补偿,故在速度收敛后仍产生波动,且通信延时越大,产生的波动幅值也越大,从而导致车辆队列的不稳定行驶.而本文所提控制器考虑了通信延时的间距补偿,缓解了由通信延时产生的车辆速度波动.

图4 PLF 拓扑下车辆队列的速度图Fig.4 Velocity profile for a platoon under PLF topology
图5 是加速度图.由图5(a)和5(b)可知,在加速阶段,文献[16]的控制器作用下跟随车辆最大加速度振幅为1.7 m/s2,且跟随车辆加速度更易受到通信延时的影响,最大通信延时0.03s 的情形下,加速度波动幅度最大约0.5m/s2.而图5(c)和5(d)表明本文所提控制器作用下跟随车辆最大加速度振幅为1.0 m/s2,在最大通信延时0.03 s 的情形下,跟随车辆加速度几乎不受影响.因此所提控制器能更好地保证车辆加速度的平稳性和抑制通信延时的干扰.
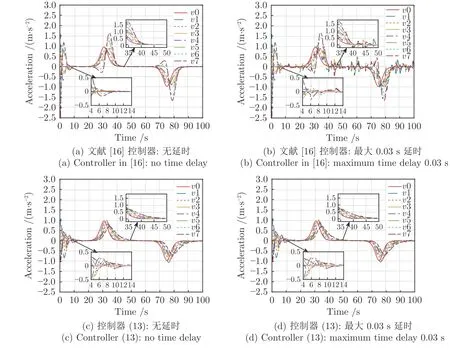
图5 PLF 拓扑下车辆队列的加速度图Fig.5 Acceleration profile for a platoon under PLF topology
图6 是间距误差图.由图6(a)和6(b)可知,跟随车辆的位置间距误差最终收敛到一致,表明在文献[16]的控制器作用下,车辆能够以队列模式行驶,但容易受到通信延时的影响,从而导致车辆队列间距的波动.图6(c)和6(d)表明在本文所提控制器作用下不仅间距误差能够收敛到一致,而且能够很好抑制通信延时的影响.此外,领导车辆减速过程中间距误差始终为正,且没有负的超调,表明所提控制器能够保证车辆队列行驶的安全性.因为本文在设计控制器时考虑了车辆跟驰作用.

图6 PLF 拓扑下车辆队列的间距误差图Fig.6 Spacing error profile for a platoon under PLF topology
3.2 TPF通信拓扑结构下的仿真分析
考虑TPF 通信拓扑结构,在无通信延时和最大0.03 s 通信延时情况下,文献[16]的控制器和本文所提控制器(13)作用下的位置、速度、加速度和间距误差轨迹如图7~10 所示.图7 是位置图.由图7(a)和7(b)~7(d)可知,在TPF 通信拓扑结构下,文献[16]的控制器和本文所提控制器仍能在无通信延时和最大0.03 s 通信延时情形下,使领导车辆和跟随车辆保持相同间距行驶.
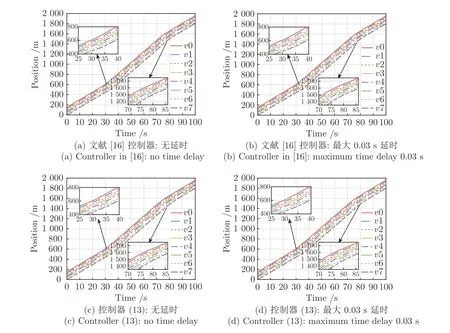
图7 TPF 拓扑下车辆队列的位置轨迹图Fig.7 Position trajectory profile for a platoon under TPF topology
图8 给出了所有车辆的速度曲线.根据图8 可知,领导车辆的运动状态可分为加速、匀速和减速三个阶段,最终跟随车辆的速度都收敛到与领导车辆一致.进一步由图8(a)和8(b)可知,在文献[16]的控制器作用下通信延时使跟随车辆的速度产生波动,最大波动约为0.2 m/s,且相对于PLF 通信拓扑结构下的波动更显著.由图8(c)和8(d)可知,本文所提控制器由于考虑通信延时的间距补偿,能够很好适应通信延时带来的扰动,且相对于PLF 通信拓扑,在领导车辆速度改变时跟随车辆速度有更剧烈的变化.
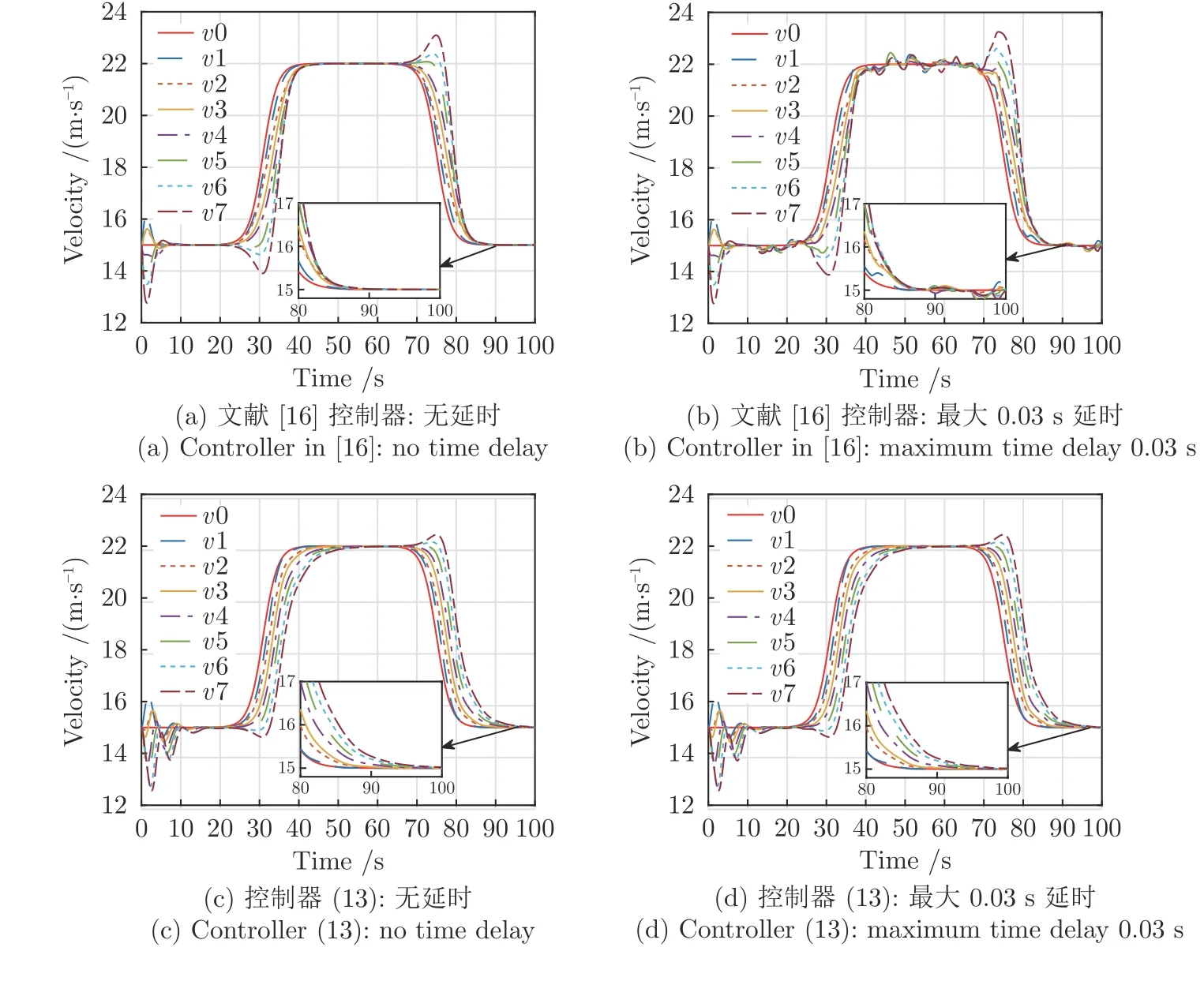
图8 TPF 拓扑下车辆队列的速度图Fig.8 Velocity profile for a platoon under TPF topology
图9 是加速度图.根据图9 可知,跟随车辆的加速度在领导车辆经过加速和减速阶段后仍能与领导和车辆保持一致.由图9(a)和9(b)可知,在文献[16]的控制器作用下,跟随车辆的加速度受通信延时的影响较大,最大波动约0.6m/s2,且比PLF通信拓扑结构下更显著.图9(c)和9(d)说明,本文所提控制器能够使跟随车辆的加速度在通信延时的影响下仍保持平滑,因此可保证更好的乘坐舒适性,且相比TPF 通信拓扑,跟随车辆加速度的幅值会随着车辆编号的增大而略微增大,这与文献[10]中描述的车辆队列的稳定性与领导车辆和跟随车辆的通信连接关系紧密的结论相吻合.
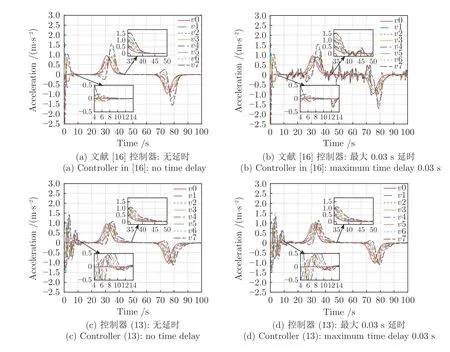
图9 TPF 拓扑下车辆队列的加速度图Fig.9 Acceleration profile for a platoon under TPF topology
图10 是间距误差图.根据图10 可知,跟随车辆能与领导车辆能够保持稳定的队列行驶.图10(a)和10(b)表明在文献[16]的控制作用下通信延时会造成跟随车辆间距误差的波动.且在领导车辆速度发生变化时,跟随车辆的误差间距会产生超调,因此在与前车距离较近时可能导致碰撞风险.而在本文所提控制器的作用下通信延时对于误差间距的影响较小,且在领导车辆速度发生变化时,跟随车辆的间距误差没有产生超调,可以避免碰撞风险.
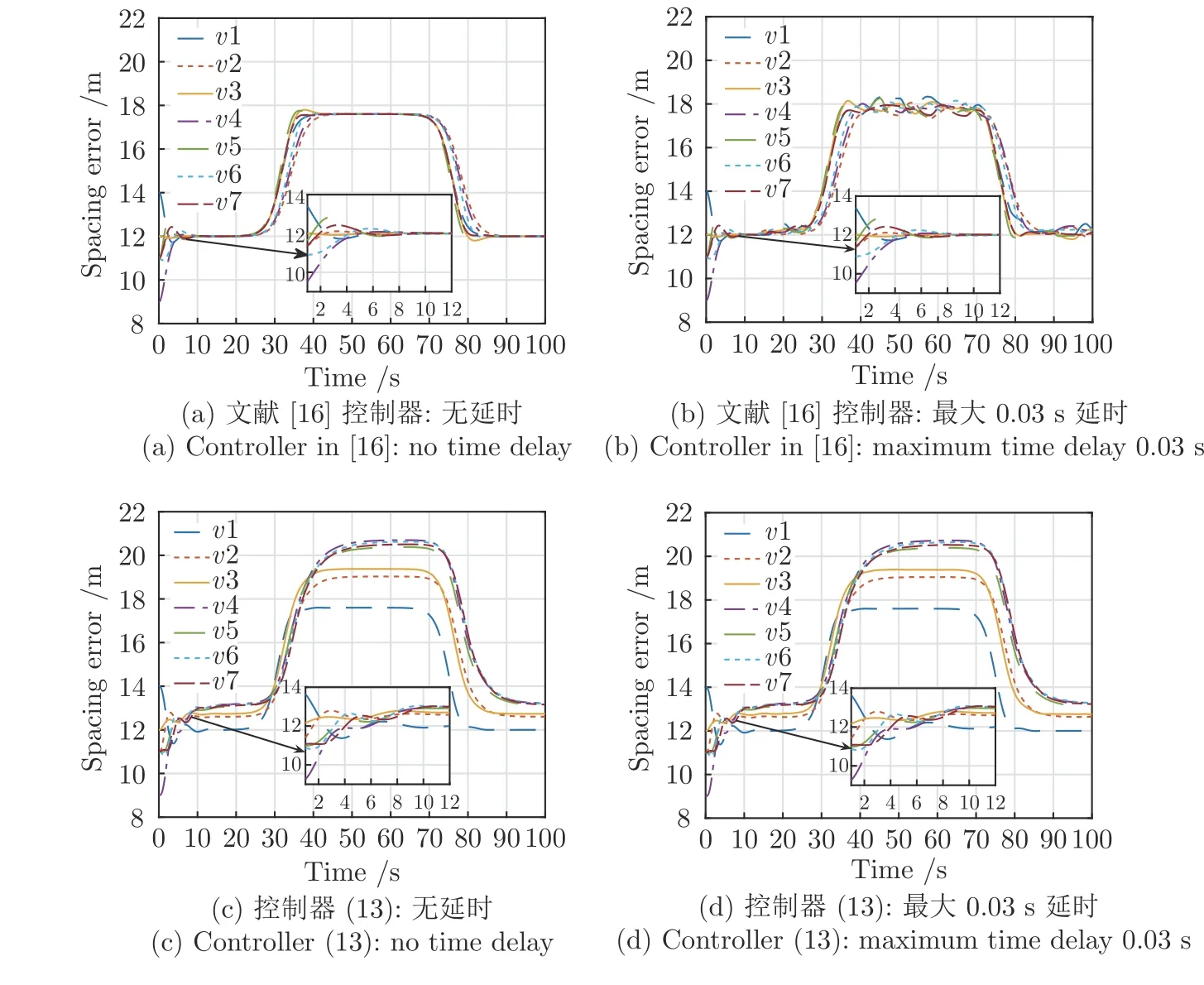
图10 TPF 拓扑下车辆队列的间距误差图Fig.10 Spacing error profile for a platoon under TPF topology
4 结论
本文考虑车辆间的非线性作用和通信延时的影响基于车辆三阶动力学模型提出一种分布式异质车辆队列非线性纵向控制器.保证车辆在通信延时的影响下仍能以队列模式行驶并且避免了负误差间距的产生,即满足车辆行驶的安全性.然后,通过Lyapunov-Krasovskii 定理证明了所提控制器的稳定性,并得出通信延时上界.最后,考虑无通信延时和最大0.03 s 通信延时两种场景,通过数值仿真对比验证了文献[16]的控制器与本文所提控制器在TPL 和PLF 通信拓扑结构下的控制效果,并得出由于考虑间距补偿和车辆跟驰行为特性,本文所提控制器在两种通信拓扑结构下均能更好地抑制通信延时带来的波动和避免碰撞风险.
附录A
矩阵S的Hurwitz 稳定条件分析:令λ为矩阵S的特征根,则有

根据引理1,其各阶主子式D1,D2,D3为
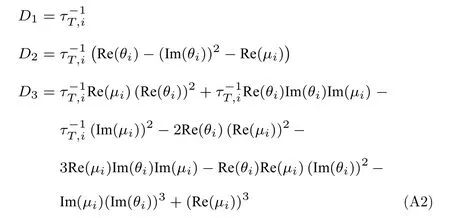
其中,θi是的第i个特征值,μi是的第i个特征值.
因此,根据引理1,可得矩阵S是Hurwitz 稳定的条件为ki,w>0,ki,p>0,ki,v>0,且D1,D2,D3均为正.
附录B
根据车辆动力学模型(4)可得

对式(B1)进行Laplace 变换L(·)

当i=2,···,N时,
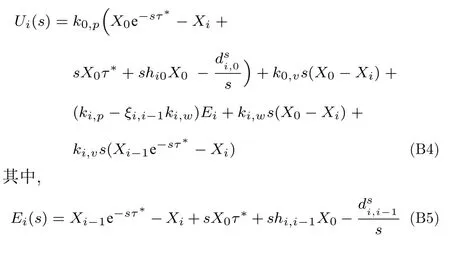
将式(B4)代入式(B2)可得:
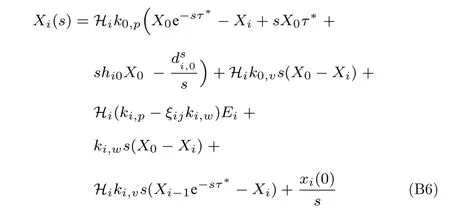
当i=1 时,
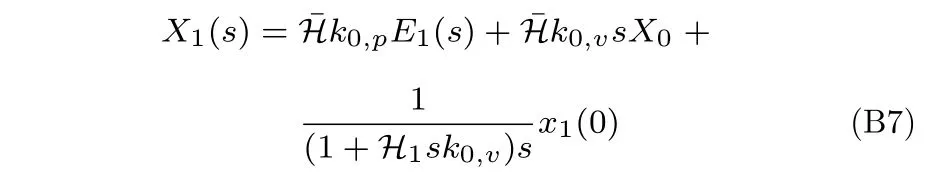
其中,
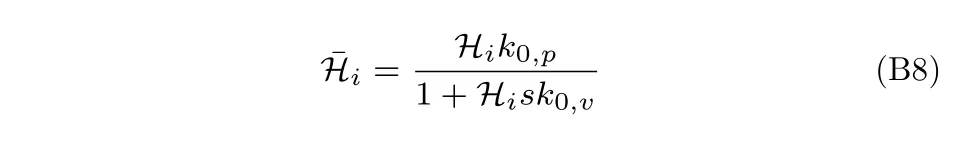
于是将式(B7)代入式(B5)可得:

假设车辆队列满足稳定性,那么可以得到h2,0=h2,1+,于是由式(B13)可得
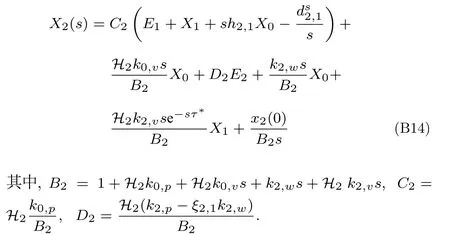
将式(B14)两边同时减去X1e-τ*s,且根据式(B5),可将式(B14)改写为

根据式(B7)和式(B9),分别将X1和X0代入式(B15)中可得:

同理推广可得:
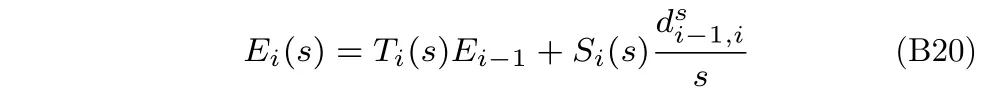
其中,


