干扰观测器与滑模控制结合的机械臂跟踪控制

周名侦，廖志青

（1.广东交通职业技术学院，广东 广州 510800；2.华南理工大学广州学院，广东 广州 510800）

1 引言

当前机械臂越来越多地应用于高精密产品装配、手术治疗等方面，对机械臂末端定位和减小抖振提出了更高要求，但是由于设计公差、参数变化、建模误差和外部扰动等原因使机械臂精确控制成为一个难点，具有重要的研究价值。总得来讲，机械臂轨迹跟踪控制方法可以分为PID控制、鲁棒控制、模糊控制、神经网络控制等。PID控制具有不依赖机械臂模型的优点，但是PID控制的启动力矩过大，容易损伤机械臂，系统稳定后运动品质较差[1]。

鲁棒控制对外部扰动、参数变化等有很好的控制效果，文献[2]将自适应算法与鲁棒控制相结合，有效减小了系统可变化参数对控制效果的影响；模糊控制主要依赖专家经验设计模糊控制器，最大的优点是无需建立控制对象的数学模型，缺点是调节参数多、工作过程繁琐，模糊逻辑要求专家经验[3]。

神经网络控制具有学习能力、容错能力和鲁棒性，在机械臂控制中应用较多，缺点是需要大量的训练和学习样本[4]，文献[5]使用神经网络逼近系统模型，使用鲁棒控制削弱逼近误差和外界干扰，取得了较好的控制效果。

研究机械臂轨迹跟踪控制问题，对于系统存在的内部或外部扰动，设计了干扰观测器和非线性滑模控制相结合的轨迹跟踪方法，旨在提高机械臂轨迹跟踪的精度和速度。

2 机械臂建模与控制方案

2.1 机械臂动力学模型

机械臂动力学模型建模方法包括牛顿-欧拉法和拉格朗日方程法两种，其中拉格朗日方程法无需研究相互间的作用力，更加简捷，因此使用拉格朗日方程法建立机械臂动力学模型，其表达式为：

式中：qi—各关节角位置；Ti—各连杆控制力矩；L—拉格朗日算子，

L=K-P；K—机械臂系统总动能；P—机械臂系统总势能。

机械臂系统总动能K和总势能P的计算方法可参考文献[6-7]，这里不再赘述。将机械臂系统动能与势能代入式（1），得机械臂动力学方程为：

式中：M(q)—机械臂惯量矩阵；C(q，q˙)—向心力和哥氏力矩阵之和；g(q)—重力矩阵；T—控制力矩；q—关节角位置矩阵。

2.2 控制方案

机械臂轨迹跟踪误差来源于以下几个方面：（1）机械臂零部件的设计公差、装配误差等；（2）未建模动态的存在；（3）外部干扰的影响；（4）机械臂参数的变化。将以上扰动或误差分为可观测部分和不可观测部分，对于可观测部分扰动，通过设计干扰观测器估计扰动大小，在控制器中进行补偿；对于不可观测部分，使用滑模变结构进行控制，达到提高控制精度的目的。本文设计的机械臂轨迹跟踪控制方案，如图1所示。

图1 机械臂轨迹跟踪控制方案Fig.1 Manipulator Trajectory Tracking Control Scheme

图中：qd—机械臂期望角位置；x1—角位置误差；T0—滑模控制器输出控制量；T—扰动补偿后控制量；d—可观测扰动；d^—扰动观测值；Td—补偿力矩；q—机械臂实际角位置。

3 干扰观测器设计

3.1 干扰观测器设计原理

干扰观测器设计原理是将系统扰动前状态与扰动后状态输入到观测器进行对比，将其差值作为扰动量的估计值，原理框图，如图2所示。

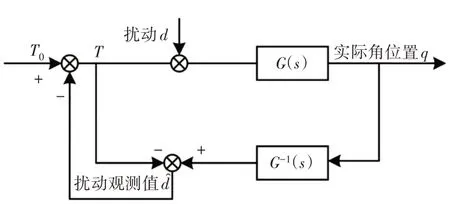
图2 干扰观测器原理图Fig.2 Principle of Disturbance Observer

图2中G(s)为机械臂系统传递函数，扰动观测值为：

3.2 干扰观测器实现方法

干扰控制器实现的基本思路是，使用扰动实际值与观测值之间的误差对观测值进行调整，达到减小误差的目的。基于此思路，将干扰观测器初步设计为：

因此只要令L(q，q˙)=diag(c1，c2，…，cn)，且ci＞0，i=1，…，n，就能够保证干扰观测器的渐进稳定性，且观测器的收敛速度通过改变ci值进行调整。

为了给出干扰观测值的计算方法，定义二维辅助向量z∈R2为：

3.3 加入干扰观测器的动力学模型

图1中前馈补偿模块设置为单位矩阵，即Td=d^。当机械臂系统中存在扰动d时，若控制系统中不加入干扰观测器，则机械臂系统动力学方程为：

对比式（10）与（11）可知，加入扰动观测器后，系统的扰动力矩由d减小为观测误差e，由此可以看出，加入干扰观测器可以有效减小扰动力矩。

4 非线性滑模控制器设计

机械臂系统为常见的非线性系统，且存在外部干扰和未建模动态等诸多不确定因素，第3节中使用干扰观测器减小了可观测扰动的影响，对于不可观测扰动和其他不确定因素，这里设计非线性滑模控制器削弱其影响。

4.1 滑模面设计

滑模控制包括两个关键内容：（1）滑模面的设计；（2）依据滑模面设计控制律[9]。滑模控制是指通过控制量的切换，使系统状态在滑模面上滑动，直至运动到系统原点。对于任意一个系统，由系统状态构造一个切换面s=0，此切换面将系统空间分为s＞0和s＜0两个部分，在切换面s=0上存在A、B、C三类点，如图3所示。点A称为穿过点，点B称为起点，点C称为止点，若某个平面或某个区域全部为止点，则此平面或此区域称为滑模面，系统状态在滑模面上的运动称为滑模运动[10]。

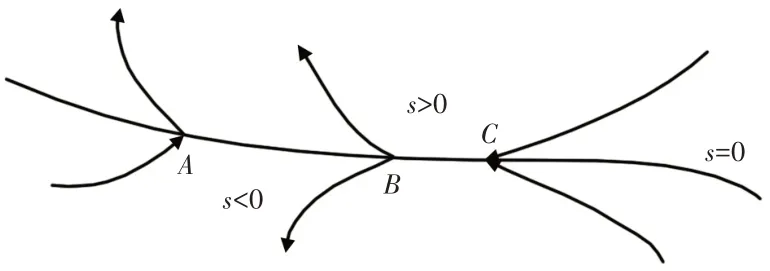
图3 切换面示意图Fig.3 Switching Surface Sketch

因此，式（13）设计的切换面s= 0 是滑模面，且具有渐进稳定性。

4.2 控制律设计

因为机械臂系统中存在不可观测扰动和未建模动态等不确定因素，控制律设计为等效控制项和变结构控制项之和，等效控制项用于控制系统确定部分，变结构控制项用于控制系统不确定部分，即用于控制不确定因素对系统的影响，增加系统鲁棒性，此时控制律为：

式中：Teq—等效控制项；

Tvss—变结构控制项。

（1）等效控制项Teq的设计方法。等效控制项用于控制系统的确定部分，当系统状态进入滑模面后，能够控制系统状态在滑模面内运动，直至滑动到原点，此时要求s=0且s˙=0，将式（12）与（14）代入s˙=0，得：

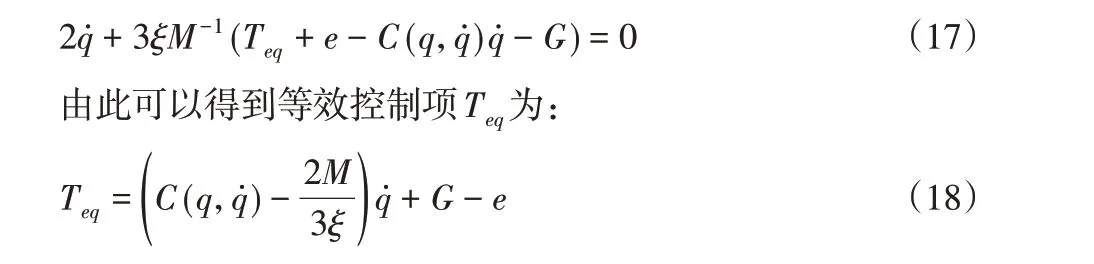
（2）变结构控制项的设计方法。变结构控制项用于控制系统的不确定部分，鉴于准连续高阶滑模控制具有收敛速度快、控制精度高、鲁棒性好、抖振相对较小等优点，本文使用准连续高阶滑模设计变结构控制项Tvss，参考文献[11]可知，变结构控制项Tvss为：

式中：k^—自适应滑膜增益，要求自适应增益k^ ≥Δmax，Δmax-不确定因素的上界。

将式（18）和式（19）代入式（16），可以得到最终使用的非线性滑模控制律。

5 仿真验证

这里设置三组仿真实验，（1）在不加入干扰观测器的情况下，使用传统滑模控制对机械臂轨迹进行跟踪；（2）在不加入干扰观测器的情况下，使用非线性滑模控制进行轨迹跟踪；（3）在加入干扰观测器的情况下，使用非线性滑模控制进行轨迹跟踪。通过比较一、二组实验，可以比较传统滑模控制与非线性滑模控制的跟踪效果；通过比较二、三组实验，可以看出干扰观测器在轨迹跟踪中的作用。

5.1 仿真初始条件设计

仿真实验在Matlab/Simulink平台上执行，对照图1将Simulink软件中各相应模块连接，构造出机械臂轨迹跟踪的Simulink图。以两连杆两关节刚性机械臂为控制对象。对于式（10）给出的机械臂动力学方程，各矩阵为：

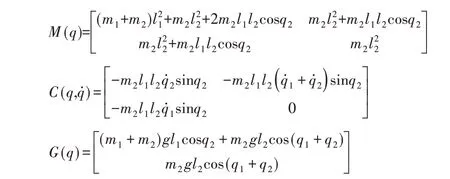
式中：g=9.8m/s2—重力加速度；

m1、m2—连杆1和连杆2的质量；

l1、l2—连杆1和连杆2的长度；

q1、q2—连杆1和连杆2转动角度，如图4所示。

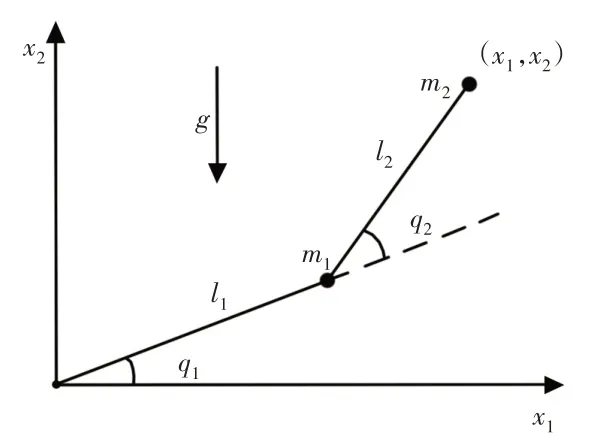
图4 两连杆两关节机械臂Fig.4 Manipulator with Two Linkages and Two Joints

式（10）中的扰动力矩d考虑库伦摩擦和粘性摩擦，即两连杆扰动均为d=zsgn(q˙)+kq˙，其中z=0.5、k=1。连杆1和连杆2初始转动角度为q1=0、q2=0，期望轨迹为qd=[sint，sint]。

仿真用机械臂的参数为：m1=1kg，m2=1.5kg，l1=1.0m，l2=0.8m。

5.2 轨迹跟踪结果及分析

在不加入干扰观测器情况下，传统滑模控制对机械臂轨迹跟踪的结果如，如图5所示。非线性滑模控制对机械臂轨迹的跟踪效果，如图6所示。

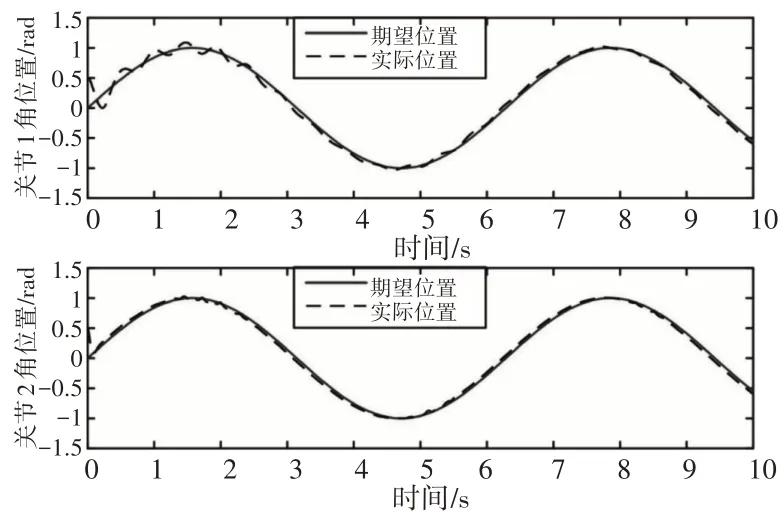
图5 传统滑模控制的轨迹跟踪结果（不加入观测器）Fig.5 Trajectory Tracking Result by Traditional Sliding Mode Control without Observer

图6 非线滑模控制的跟踪结果（不加入观测器）Fig.6 Trajectory Tracking Result by Nonlinear Sliding Mode Control without Observer

对比图5和图6对机械臂轨迹的跟踪效果，对于关节1的轨迹跟踪，图5使用传统滑模控制，在2s时依然存在较大的抖振，3s时才逐渐稳定；图6使用非线性滑模控制，在0.4s时就能够稳定跟踪期望轨迹，不存在长时间的抖振现象。对于关节2，传统滑模控制和非线性滑模控制对轨迹的跟踪均存在一定的滞后性，跟踪误差较大。总的来讲，与传统滑模控制相比，非线性滑模控制能够有效减小抖振，具有更好的控制效果。这是因为非线性滑模控制律依据非线性滑模面设计，更加符合机械臂非线性系统的特点，同时非线性滑模控制律中考虑了不确定因素的影响，因此非线性滑模控制效果优于传统滑模控制。

在加入干扰观测器的情况下，使用非线性滑模控制跟踪机械臂的期望轨迹，结果，如图7所示。

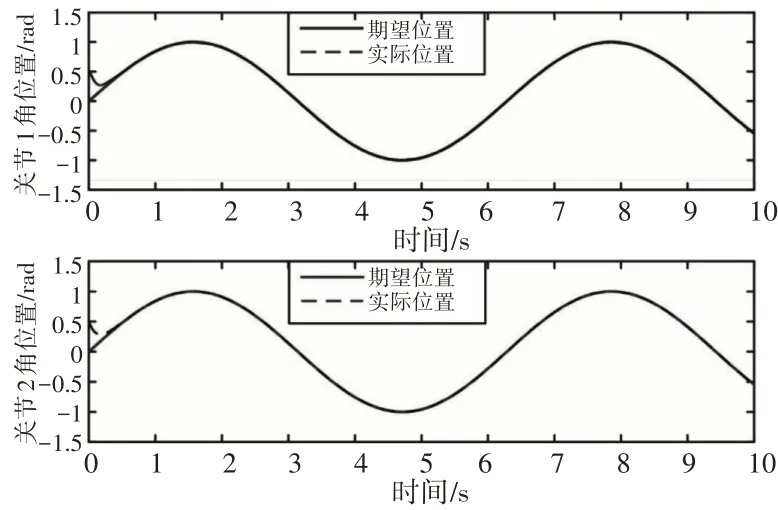
图7 非线性滑模控制的跟踪结果（加入观测器）Fig.7 Trajectory Tracking Result by Nonlinear Sliding Mode Control with Observer

对比图6和图7加入扰动观测器前后的轨迹跟踪效果，加入扰动观测器后，关节1和关节2在0.2s后能够精确跟踪期望轨迹，跟踪误差几乎为0；而未加入扰动观测器时，关节1和关节2均存在一定的跟踪幅值误差和相位误差。跟踪效果的差别充分证明了扰动观测器在轨迹跟踪中的有效性，这是因为通过对扰动的观测，进而对控制力矩进行补偿，是一种消除扰动影响的主动措施，能够有效抑制扰动产生的轨迹跟踪误差。

为了进一步比较传统滑模控制、非线性滑模控制、加入干扰观测器的非线性滑模控制结果，统计三种方法稳定跟踪的时间和第一次到达期望轨迹后的最大跟踪误差，结果，如表1所示。

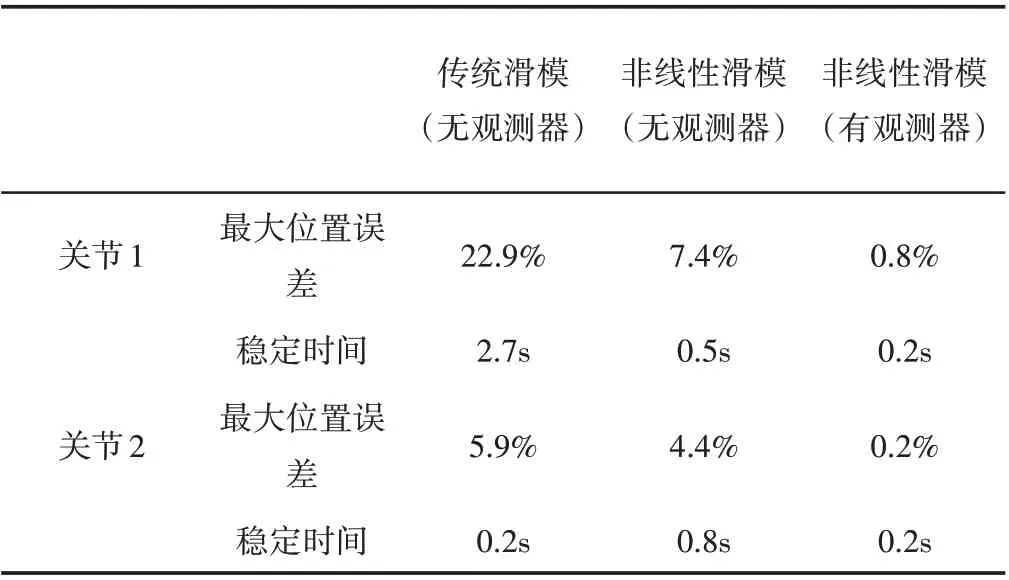
表1 不同方法的跟踪结果Tab.1 Tracking Result by Different Method

由表1中数据可知，加入干扰观测器的非线性滑模控制的轨迹跟踪误差比另外两种方法减小了一个数量级以上，稳定跟踪轨迹的时间也最短，这是因为系统中存在的可观测扰动，使用观测器进行观测后及时调整控制力矩，主动消除可观测扰动的影响；对于不可观测扰动，使用非线性滑模控制减小其带来的抖振和跟踪误差，因此取得了极高的控制精度和较好的控制效果。

6 结论

这里研究了机械臂的轨迹跟踪控制问题，将扰动分为可观测部分和不可观测部分。对于可观测扰动，设计了干扰观测器，根据观测值设计力矩补偿值，减小可观测噪声影响；对于不可观测扰动，设计了非线性滑模控制器，用于减小不可观测扰动引起的抖振和跟踪误差，最终取得了较高的跟踪精度和较好的跟踪效果。