基于响应面法的整车操纵稳定性多目标优化
张龙飞,范 英,谢纯禄,晋民杰
(太原科技大学交通与物流学院,山西 太原 030024)
1 引言
操纵稳定性是汽车最重要的性能之一,关乎着汽车的品质和安全,在产品开发的过程中占据着重要地位。另一方面,基于虚拟样机的研究技术发展较快,奔驰公司、上海大众汽车公司、福特汽车公司、吉林大学等国内外知名企业机构已经将此技术运用到操纵稳定性的分析评价中,并对操纵稳定性进行优化研究[1],文献[2]基于工程自卸车建立模型,通过改变其悬架硬点位置,很好的提升了整车的操纵稳定性。文献[3]以FSAE赛车为原型搭建整车模型,利用多目标优化的思想对前悬架定位参数进行优化,改善了汽车操纵稳定性。文献[4-5]基于某国产皮卡车,分析和优化前悬架定位参数以提高整车操稳性,并利用国标试验对其优化的结果进行评价验证。然而这些关于操纵稳定性的优化研究主要集中在优化悬架结构上,对影响操纵稳定性的其他因素的优化研究相对较少。因此基于某车型轿车,以提高车辆操纵稳定性为目的,对多个参数进行详细分析和优化设计。结果表明,优化后的操纵稳定性得到显著改善。
2 整车动力学模型搭建和验证
2.1 整车模型搭建
在ADAMS/Car中,参照某车型轿车利用其尺寸参数和力学参数建立各个子系统,并完成整车装配[6-7],如表1所示。

表1 整车相关参数Tab.1 Vehicle Related Parameters
该车型的前后悬架分别采用麦弗逊独立悬架和拖拽臂附扭力杆半独立式后悬架,转向器为齿轮齿条式转向器,制动器为四轮盘式制动,轮胎型号为195/60 R15 88H,搭建的模型,如图1所示。

图1 整车多体动力学模型Fig.1 Multi-Body Dynamic Model of Vehicle
2.2 整车模型验证
为了验证仿真动力学模型的准确性,利用回正试验和脉冲试验对模型进行仿真,将仿真结果与路试结果进行比较,其结果[8],如图2所示。从图2模型验证的比较结果可以看出,在相同工况下,仿真模型和试验样车的稳定时间和横摆角速度稳态值相差不大,在允许误差范围内。表明该模型具有较高的仿真精度,可用于后续仿真研究。
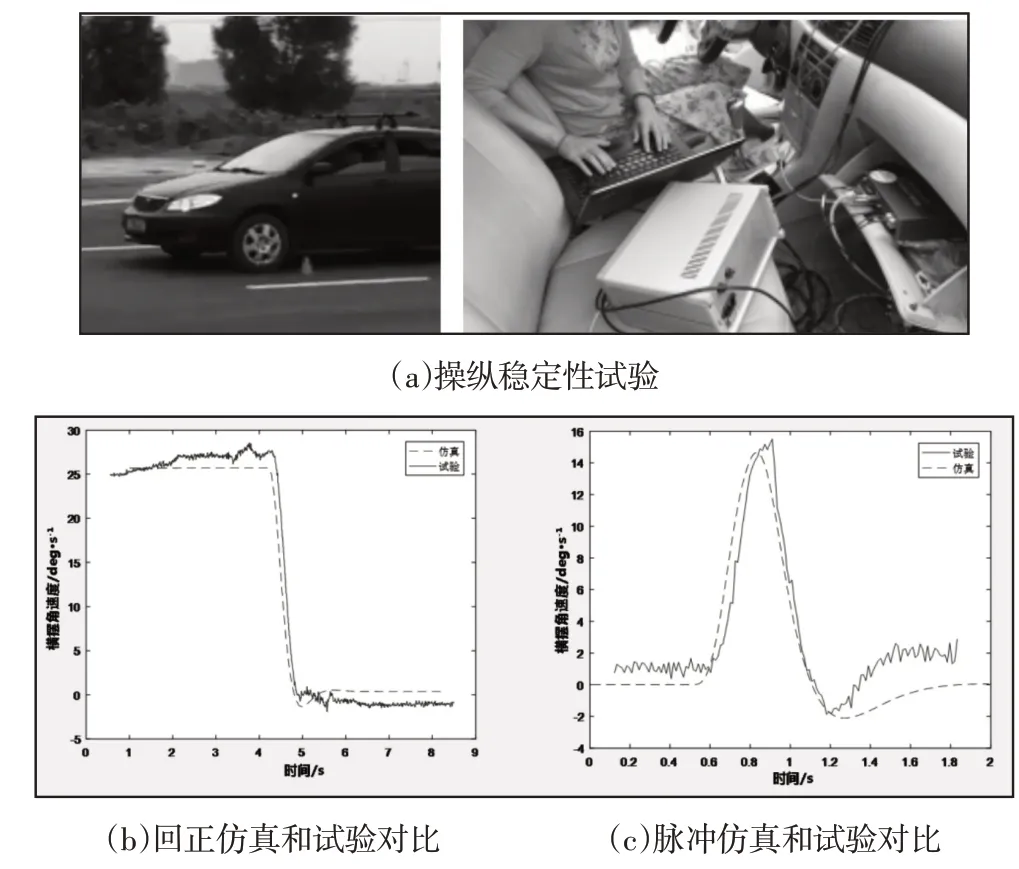
图2 实车试验及模型验证Fig.2 Vehicle Test and Model Verification
3 参数对汽车操纵稳定性的影响
汽车的转向特性是操纵稳定性极其重要的组成部分,通常用稳态横摆角速度增益来表示[9]。
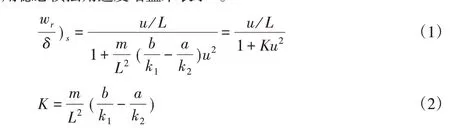
式中:K—稳定性因数,s2·m-2。
这里,K为评价汽车稳态响应的重要参数,从式(2)中可以看出,整车载荷m、质心至前后轴的距离a,b以及前后轮胎侧偏刚度k1,k2对汽车的操纵稳定性有很大的影响。
此外,四轮定位参数、前后悬架弹簧刚度和阻尼等参数都会影响汽车的稳态和瞬态响应特性,但定位参数中前束的作用是为了补偿外倾角的影响,取值大小由外倾角计算而来,所以在此不考虑前束对操稳性的影响[10]。
根据现行汽车操纵稳定性试验国家标准,利用阶跃试验中横摆角速度、侧向加速度和车身侧倾角来研究各个参数对汽车操纵稳定性的影响。
从图3的仿真结果可以看出,增大外倾角、后倾角或减小内倾角可略微降低三个指标的响应时间和稳态值,提高汽车的操纵稳定性。轮胎的侧偏刚度对汽车的操纵稳定性有着较大影响,可大幅度的提升汽车性能。质量的增大使得汽车行驶更加稳定,响应速度加快,改善了车辆瞬态响应,但同时车身侧倾角变大,降低了乘坐舒适性。
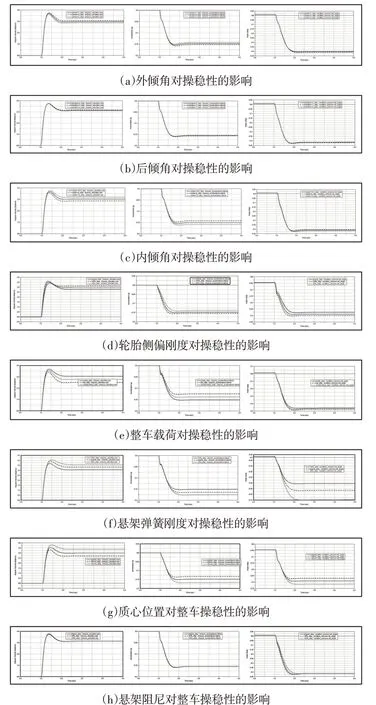
图3 各参数对汽车操稳性的影响Fig.3 The Influence of Various Parameters on Vehicle Handling Stability
悬架弹簧刚度的增大降低了车身侧倾角的大小,提高了车辆的操纵稳定性。质心位置的改变对操稳性影响较为显著,质心位置向前移动,有利于增加不足转向特性,使得三者的稳态值显著降低,响应时间缩短,操稳性得到改善。悬架阻尼对汽车横摆角速度和侧向加速度几乎没有影响,但增大悬架阻尼会使得车身侧倾角减小,提升汽车的操纵稳定性。
4 操纵稳定性优化设计
4.1 优化设计方法
响应面法也就是常说的RSM,是一种数学统计方法,通过输入自变量来确定最佳的响应值,并且将复杂的、关系不明确的函数用多项式来表示,操作简便且拟合精度高[11]。根据本文的实际情况,选取构建响应面近似模型进行多目标优化。
响应面一阶和二阶多项式模型基函数如下;

式中:y—响应目标;x1,x2,...,xn—设计变量;βi—多项式系数。
因为响应面二次多项式模型拟合更为精确,应用较为普遍。因此采用二次多项式模型进行拟合分析[12-13]。
4.2 优化设计基本要素
4.2.1 设计变量
基于上述各参数对操纵稳定性的影响分析,按照灵敏度大小选取对汽车操稳性影响较大的参数进行优化设计,又因为整车载荷、轮胎侧偏刚度和质心位置在试验中不易调校,不适合作为变量。综合考虑后取前轮外倾角α、主销后倾角β、内倾角δ、前后悬架弹簧刚度kf,kr作为设计变量,可将5个变量组成一个设计变量向量x:

式中:f—悬架固有频率,Hz;i—弹簧行程与车轮行程之比;m—簧载质量,kg。
综上所述,设计变量的优化范围,如表2所示。
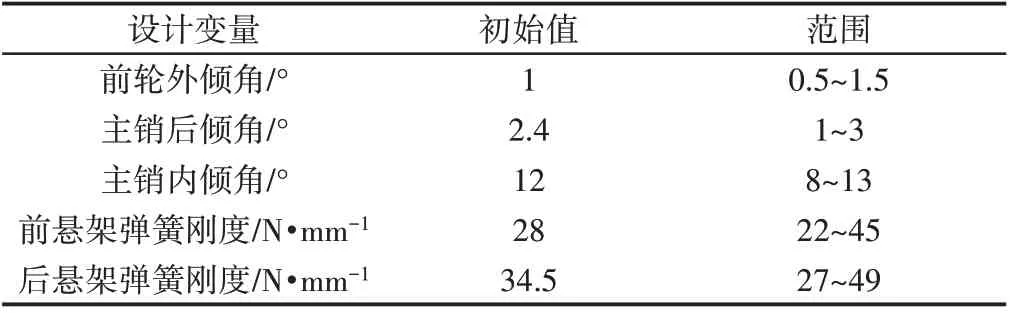
表2 设计变量优化范围Tab.2 Design Variables and Optimization Scope
4.2.3 目标函数
优化的目的在于提升汽车的操纵稳定性能,所以目标函数的选取至关重要。这里采用阶跃输入下的时域响应对汽车的操纵稳定性进行评价,时域响应又分为稳态响应和瞬态响应[9],稳态响应通常用横摆角速度增益来评价,瞬态响应则包括固有圆频率、响应时间、超调量等参数,其中响应时间反映了系统执行操作速度的快慢,超调量反映了系统执行上的误差。因此在研究操纵稳定性瞬态响应品质的好坏时,常用这两个相互矛盾的参数来作为目标函数[14]。

4.3 响应面二次多项式模型的建立
以α、β、δ、kf、kr为设计因子,多目标函数F(x)为响应目标,利用Design Expert进行试验设计。

图4 目标函数的残差概率分布图Fig.4 Residual Probability Distribution Map of Object Function

图5 部分响应曲面图Fig.5 Partial Response Surface Map

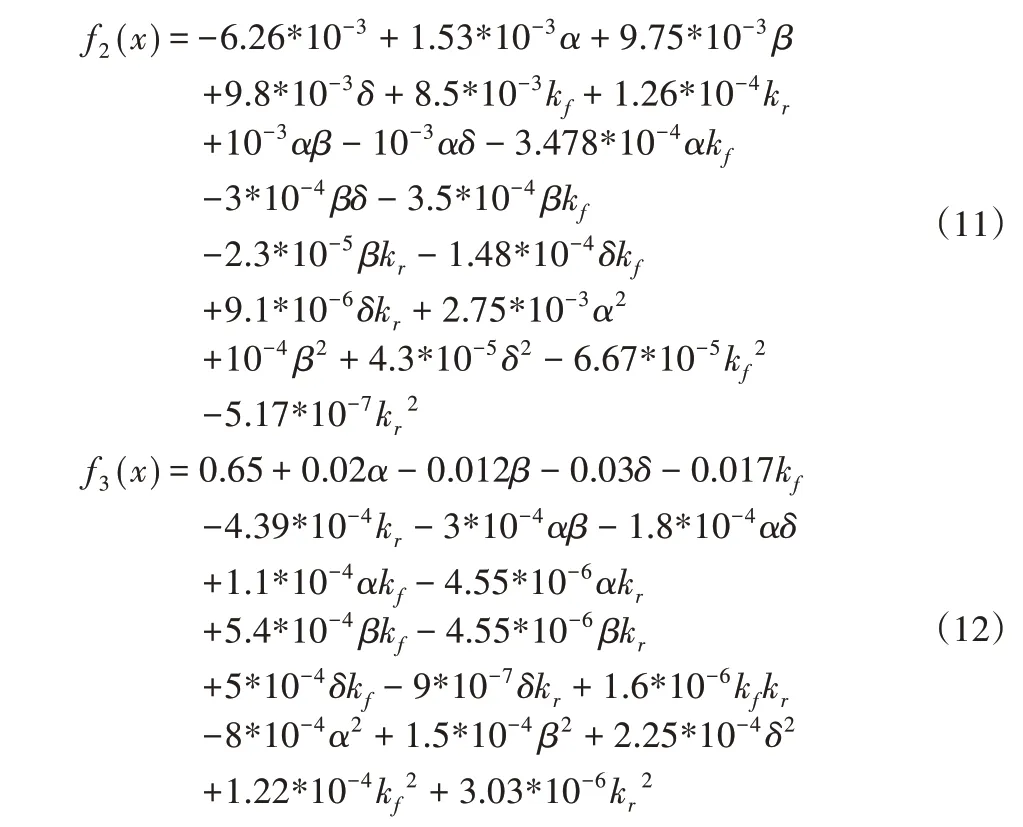
通过残差图可以看出,三个目标函数的残差符合正态分布,回归方程相关性较好。
采用加权组合法,将式(10~12)引入相应的加权因子将其组合成总的目标函数;

式中:Δfi(x)—指标i的容限值。
通过目标函数的容限值来获得加权因子,可以平衡每个目标函数的量级[15]。

利用上述回归方程得到了三个目标函数f1(x)、f2(x)、f3(x)的变化范围,即;入仿真模型后在相同工况下进行角阶跃试验,得到F(x)值为4.199,与理论预测值的误差仅为0.14%,由此可知,优化的结果正确可行。
5 操纵稳定性优化验证
5.1 仿真验证
将上述优化后的参数带入模型中分别进行阶跃和脉冲仿真试验,对比优化前后汽车时域响应特性和频域响应特性,验证优化的结果,如图6、图7所示。

图6 阶跃仿真优化前后时域响应Fig.6 Time-Domain Response Before and After Step Simulation Optimization
从图6可以看出,优化后的横摆角速度、侧向加速度和车身侧倾角稳态值均有所下降(其中横摆角速度稳态值下降12%),同时响应时间比优化前缩短了24.2%,虽然优化后的超调量略微增大,但仍满足汽车超调量的标准。从图7 中的幅频特性曲线来看,优化后较之优化前共振峰频率略微增大,稳态增益值略微减小,从相频特性曲线来看,操纵的失真程度减小。综上所述,优化后显著提升了汽车的操纵稳定性。

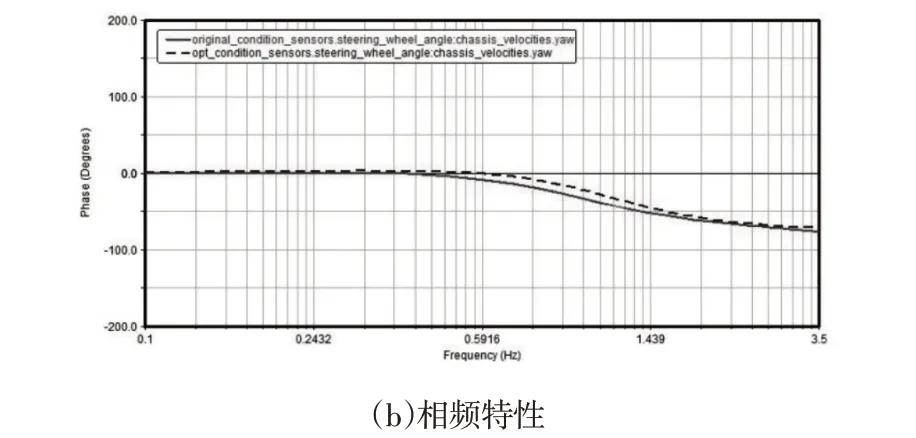
图7 角脉冲仿真优化前后频率响应Fig.7 Frequency Response Before and After Optimization of Angular Pulse Simulation
5.2 试验验证
将优化后的相应参数代入到试验车中,进行各项操纵稳定性试验,如图8所示。

图8 优化前后试验对比Fig.8 Test Comparison Before and After Optimization
从图8中可以看出,该试验车经过优化后,各工况下的横摆角速度幅值均略微减小,图8(b)、图8(c)中横摆角速度响应时间大幅缩短,图8(c)中的横摆角速度稳态值有所下降,图(d)中横摆角速度超调量有所减小。综上所述,与优化前相比,整车的操纵稳定性得到显著提高。
6 结语
(1)利用多体动力学软件ADAMS/Car建立某车型轿车的动力学模型并进行实车试验验证。通过仿真试验详细分析了各参数对汽车操纵稳定性的影响,大大降低了试验成本。
(2)以前轮定位参数和前后悬架弹簧刚度为设计变量,阶跃输入下的时域响应为目标函数,采用响应曲面模型和多目标优化理论进行参数优化,很好的改善了整车的操纵稳定性,为某车型轿车的操纵稳定性优化提供了方法。

