基于个性优势结构识别的物流师生匹配决策问题
石 甜,杨保华
(1.江苏师范大学科文学院 商学院,江苏 徐州 221116;2.江苏师范大学 商学院,江苏 徐州 221116)
0 引语
本科生导师制[1]的实施首先改变了传统的“满堂灌”教学模式,更加注重学生个性化的发展与学生的知识结构,培养学生发现问题与解决实际问题的能力。此外导师制也会促进教师不断提高自己的业务能力,在学生的学习、科研、就业等方面给予帮助。这种模式极大地促进了高校教育资源的充分利用,有利于因材施教。目前大多数学者对本科生导师制的研究主要侧重于实践效果及选择导师的影响因素。石荣传[2]将本科生导师制分为全程、年级及精英3种类型,指出实施过程中存在导师职责不明确的问题,提出高校应该明确导师职责、侧重师生互选等建议。李青[3]通过分析本科生导师制认知定位等问题,提出规范优化本科生导师的遴选过程、互选模式的创新化等建议,以提升本科生导师制的有效性。贾莉莉,等[4]通过对应用技术人才培养问题的反思,得出高校需要关注个体知识学习与实践活动,深化教学范式改革等措施。丁林[5]将导师制分为社团导师制、项目导师制、论文导师制、英才导师制4种类型,指出科学合理定位、创新实践模式和健全体制机制是导师制的三大关键影响因素。洪岑岑,等[6]根据本科生导师制的实施,提出“项目引领型”导师制具有一定的优势。
综上所述,现有的研究成果聚焦于导师制实践过程的研究,鲜有研究涉及师生匹配问题,而导师制实施成功的前提首先是要完成导师和学生“双向选择”,导师与学生的分配会对后续的指导有影响。比如,学生的知识结构、兴趣爱好是否与导师的科学研究、专业特长等相一致会对指导过程是否顺利、指导结果能否达到预期的目的、能否提升学生培养质量、促进学生成材等产生很大影响。因此,本文利用个性优势结构方法研究师生匹配问题,利用定量的方法提高学生与导师的匹配科学性与精准化,对于充分发挥学生的优势、实现学生的个性化发展具有积极的促进作用。
1 基于个性优势结构识别方法
本文首先建立以导师类型为主的综合指标评价体系,利用个体优势结构特征识别模型计算出每种导师类型的理想结构;其次,根据学生的各项指标,结合专家意见和学生自我评价,获得关于学生各项指标评价矩阵,通过二者相似度判断,根据个性优势结构识别模型求解出学生基于各项指标的理想结构;最后,构建关于导师与学生的优势结构差异度,构建0-1整数规划模型,得到最佳的师生匹配方案。
1.1 个性优势结构识别模型
个体优势特征识别是根据指标体系,利用效用函数求价值最大化,因此涉及到评价函数的选择。本文根据指标值向量构建基于理想点效用的个性优势结构特征识别的数学模型[7],即求解实际的指标值向量与理想指标值向量之间的距离,以距离的远近决定其优劣顺序。具体模型如式(1):

其中,X是观测指标值,X*是理想值是在参数ωi下X与X*之间的距离,式(1)的最优解表示在确定指标体系和理想点效用模式下,决策单元x i的优势识别结果,表现了决策单元xi的个体优势特征。
(1)当指标向量值中理想值与实际值相同时,目标函数中的变量系数为0;最优解为:达到理想值对应的变量之和为1,其他变量均为0;
(2)当指标向量值中理想值与实际值不相同时,最优解为:

其中,λi表示个体优势特征,表示优势识别结果。
1.2 导师类型理想结构识别模型
现有研究成果中,根据研究问题的不同,导师制的类型各有不同。胡绍远,等[8]在分析导师制存在的问题时,指出目前国内导师制具有全职型、学术型、思政型、辅助型4种类型。黄信瑜[9]将高校导师制分为顾问导师制、生活导师制、实习导师制、素质导师制、学习导师制及科研导师制6种类型,并对导师制的实施提出创新路径。在总结文献基础上,结合目前高校导师具体职能与当前发展现状,本文把导师主要分为:项目引导型、实践创新型、技能竞赛型、综合实力型4种类型。
因此,导师类型理想结构主要包括4个方面:项目引导型导师、实践创新型导师、技能竞赛型导师及综合实力型导师的理想结构。从实际情况出发,选择相关专业具有权威的专家对各个导师类型的各项指标给出评价数据,然后根据式(1)和式(2)计算各个类型导师理想结构。
N位专家对导师类型Mj(j=1,2,...,k),按照指标重要性给出判断矩阵VN×p,见式(3)。
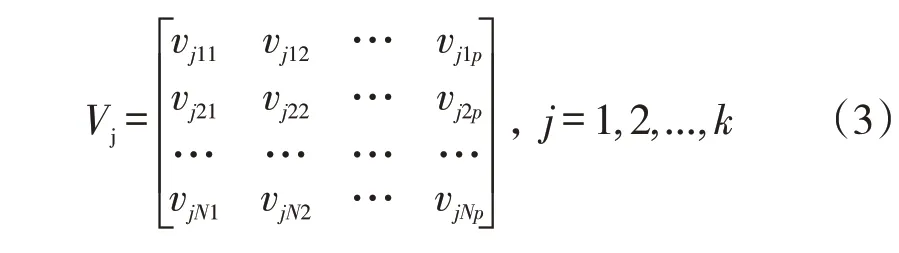
按照式(1)和式(2)的个体优势结构识别模型计算出导师类型Mj的优势识别结果V'
k,见式(4)。
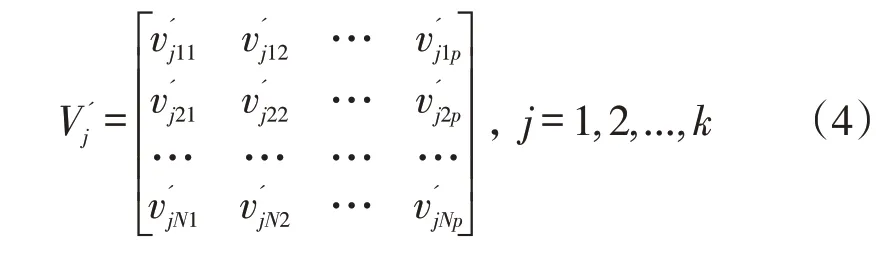
令αi为专家评价重要性权重,令,得到导师类型的优势理想结构V'j,见式(5)。
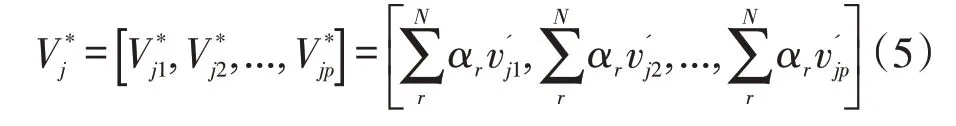
1.3 学生个性优势结构识别
评价过程存在的主观性使得指标值差异性较大,且个性优势结构特征分析主要是针对各项指标相对优劣度分析,因此个性优势结构特征分析要尽可能地避免主观性,更真实地反映学生的优势,进而为匹配决策提供一定的支持。而每位学生存在的优势各不相同,因此需要对学生的优势进行评价,得到学生优势的理想结构。本文利用专家评价和学生自己评价两种方式构建学生优势结构评价模型,进而得到最终的学生优势理想结构。
(1)学生个性优势结构专家评价。假设学生集合为G=( )G1,G2,...,GT,N位专家对学生Gk(k=1,2,...,T)的各项优势进行评价而得到的评价矩阵为B N×q,见式(6)。

根据式(1)和式(2)计算得到Gk的优势结构矩阵W N×p,见式(7)。
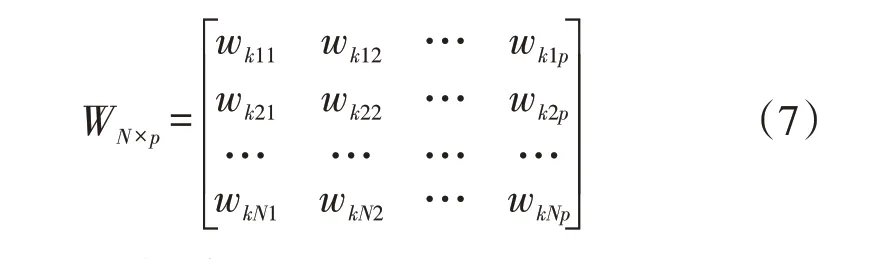
同上,令专家评价重要性权重为βs(s=1,2,...,N),则由专家评价的学生的个体优势理想结构见式(8)。
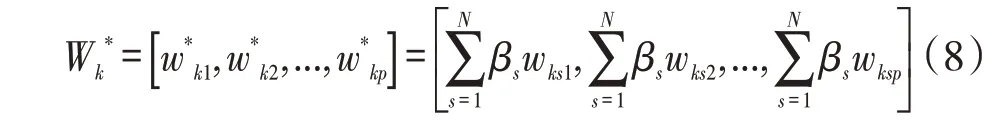
(2)学生个性优势结构自评价。根据学生自我评价值得到评价矩阵,计算过程同上述专家评价,可得到学生个性优势理想结构为,见式(9)。
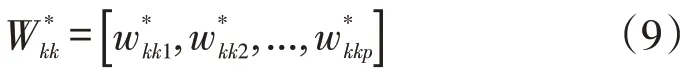
由于自我评价与专家评价的优势结构相似度是对同一个学生而言的,因此学生自我评价与专家评价的相似程度越接近,说明观点越一致;相似度越小,说明差别越大[10]。因此学生G k优势结构自我评价结果与专家评价结果相似度见式(10)。
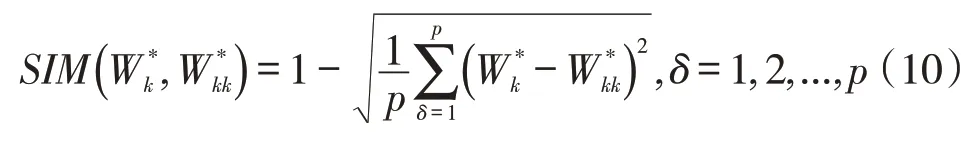
根据半数法则,如果自我评价与专家识别的相似度超过50%,则二者观点具有一致性;如果相似度小于50%,则根据二八原则确定学生Gk的优势理想结构,见式(11)。

2 基于个性优势结构识别的匹配模型
2.1 师生优势结构差异度测量方法
本文利用师生优势结构差异度衡量双方理解结构差距,具体的师生差异度计算方法见式(12)。

其中,C j表示学生Gk的优势理想结构与导师类型Mj优势理想结构之间的差异度。
2.2 基于个性优势结构识别的师生匹配模型
基于上节的师生优势结构理想差异度模型,本文利用匈牙利指派方法[11]解决导师与学生之间匹配决策问题。假设决策变量为x ij,当x ij=1时表示指派第i学生分配第j位导师,x ij=0表示不指派第i学生分配第j位导师,建立0-1整数规划模型,得到最佳的师生匹配方案,见式(13)。
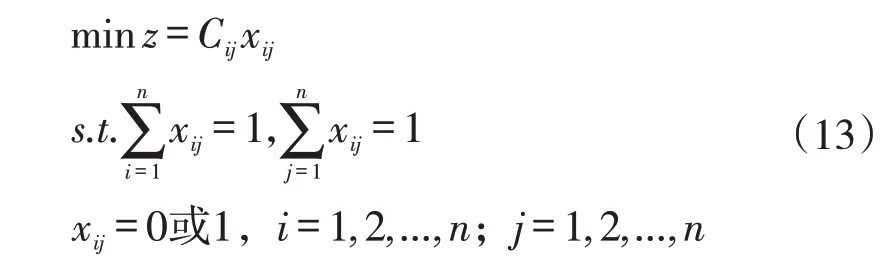
3 案例研究
不同类型的导师有着不同的优势,而且对学生具有的优势也有差别。本文以A学校的4种类型导师、10位物流专业学生为例,计算出10位学生匹配到的导师类型的理想结构,最大限度的发挥该专业学生的优势。
由于A学校拥有项目引导型、实践创新型、技能竞赛型、综合实力型等类型的教师,本文主要从外语能力、数学能力、创新能力、兴趣爱好、语言表达能力、知识储备量6个方面对物流专业学生的优势结构进行考察。
3.1 导师类型优势理想结构
本文基于研究的科学性,邀请A学校7位比较有权威的专家对各个指标进行赋值。指标赋值采用里克特量表法,1表示非常差,2表示差,3表示一般,4表示好,5表示非常好,因此可知5是指标的理想值。限于篇幅,本文仅以项目引导型导师理想结构计算过程为例。
利用专家评分法得到的原始矩阵,假设每位专家的权重相同,按照式(1)-式(4)进行计算,得到项目引导性导师的理想结构,见表1。
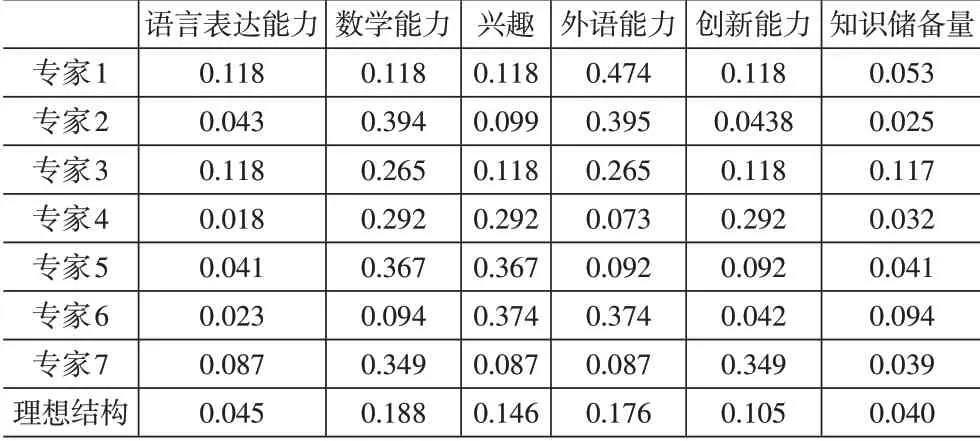
表1 项目性导师理想结构
同上述计算过程,本文可以得到4种类型导师的理想结构,见表2。

表2 四种类型导师理想结构
3.2 学生优势理想结构
(1)学生个性优势结构专家识别。本文基于研究的科学性,邀请A学校班主任、辅导员、任课老师等7位专家采用里克特量表法对10位物流专业学生的指标进行赋值。由于篇幅所限,仅以学生1的计算过程为例,并假设每位专家的权重相同,根据式(1)-式(4)进行计算,得到学生1的理想结构,见表3。
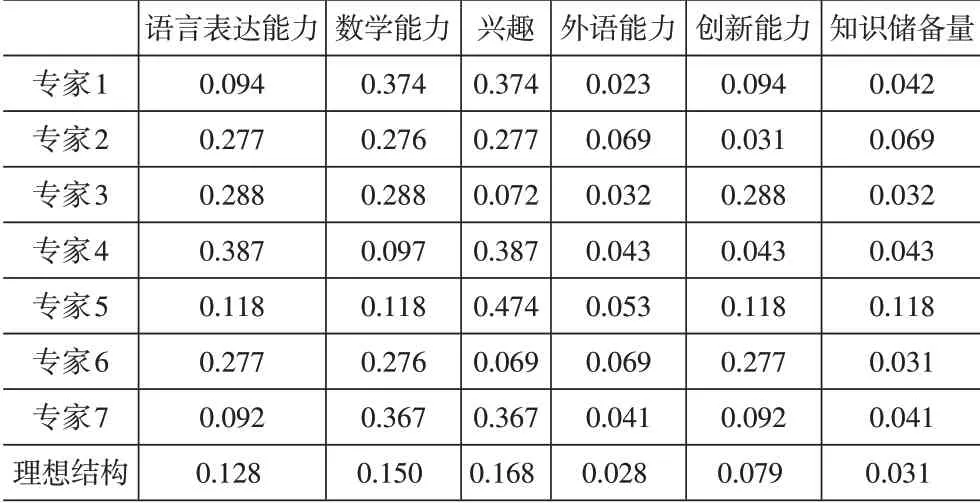
表3 物流专业学生优势结构专家评价识别结果
同理可得10位物流专业学生专家评价的理想结构,见表4。
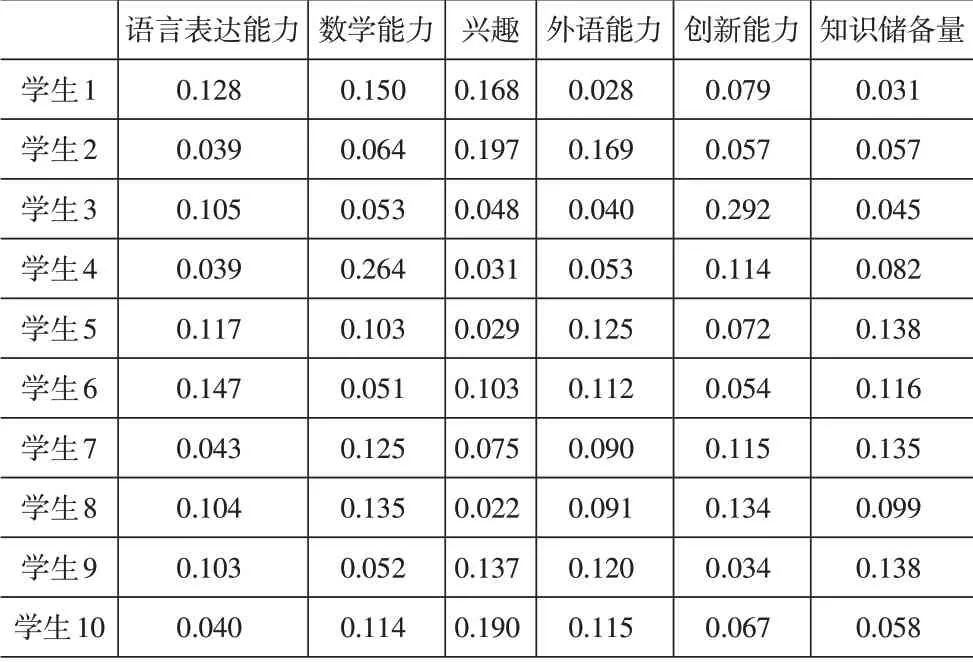
表4 物流专业学生专家识别理想结构
(2)学生个性优势结构自我识别。利用物流专业学生对自己实际情况的赋值结果,根据式(1)-式(4)进行计算,得到10位学生自我评价的优势识别理想结构,见表5。
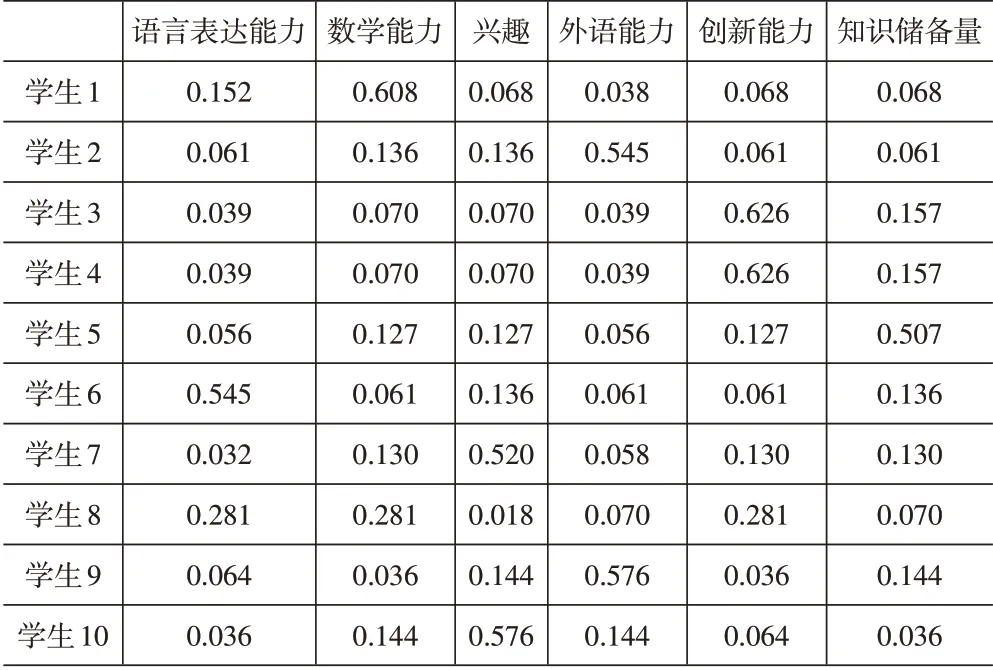
表5 物流专业学生自我评价识别理想结构
(3)学生优势理想结构。根据式(10)计算得到专家识别的理想结构和自我评价的理想结构相似度均大于50%,因此,按照式(11)综合专家识别理想结构与自我评价理想结构,得到该专业学生理想结构,见表6。

表6 物流专业学生理想结构
3.3 师生优势结构匹配模型的建立
根据上节得到的导师类型理想结构与物流专业学生的理想结构,按照式(12)得出导师与该专业学生理想结构之间的差异度,见表7。

表7 物流专业学生与教师理想结构匹配差异度测算表
由表7的差异度,利用式(13)建立0-1规划模型,由于每位类型的导师可以带多个学生,虚增多个学生进行指派,经计算得到师生匹配结果,因此师生之间的匹配方案是:学生1、2、5与项目引导型导师匹配,他们的数学能力、外语能力、知识储量优势突出,符合项目引导型导师对学生的期望;学生3、4与实践创新型导师匹配,满足实践创新型导师对学生创新能力的要求;学生8与技能竞赛型导师匹配,其优势主要表现在数学、语言表达方面,在技能竞赛中可得到充分发挥;学生7、9兴趣与外语方面的优势与综合实力型导师要求相契合。学生6、10不匹配导师,由于学生自身的条件不能满足导师的需求,需要继续学习基础的理论知识,并结合自身的优势,在下个学期继续根据优势结构进行导师匹配,进而最大限度发展学生的优势,更好的促进了导师制实施的科学性。
4 结语
以A学校4种类型导师、10名物流专业学生为例,从语言表达能力、数学能力、兴趣、外语能力、创新能力、知识储备量5个方面进行计算。进而得出结论:
(1)利用个性优势结构识别方法计算导师类型理想结构与学生的理想结构,最后根据导师类型与该专业学生理想结构之间的差异度,建立0-1整数规划模型。
(2)通过计算得到的师生匹配方案:学生1、2、5与项目引导型导师匹配,学生3、4与实践创新型导师匹配,学生7、9与综合实力型导师匹配,学生8与技能竞赛型导师匹配,学生6、10不匹配导师,需要未匹配到导师的学生继续学习基础的理论知识,再进行导师匹配。最大限度地保证学生优势的发挥,实现导师与学生的双赢。
(3)另外本文导师类型和学生理想结构计算的时候是在假设专家权重相同的情况下,未考虑到权重不同的情况;而且目前导师的类型只有4种,考虑可以根据学生的优势的不同,以提升学生的培养质量为目的,需要增加导师的类型。
总之,本文通过将师生之间的优势匹配进行量化,对于导师后期指导顺利,学生优势的充分发挥,教育资源的充分利用具有积极影响,而且个性优势结构识别方法在本科生导师制师生匹配方面的应用,突出它的实用性,为后来本科生导师制的发展提供一定的理论参考。

