基于改进PCA-RFR算法的汽油辛烷值损失预测模型的构建与分析
蒋 伟,佟国香
(上海理工大学 光电信息与计算机工程学院,上海 200000)
研究法辛烷值(RON)是反映汽油燃烧性能的最重要指标。按照车用汽油国家标准,车用汽油RON应分别达到89/92/95。中国现有技术在对催化裂化汽油进行脱硫和降烯烃过程中,普遍降低了汽油辛烷值,每降低一个单位的辛烷值约相当于损失150 CNY/t[1-4]。为了尽可能减少汽油催化裂化过程中辛烷值的损失,需要建立化工过程模型对RON损失进行预测[5-8]。由于炼油工艺过程的复杂性以及设备的多样性,催化裂化中涉及到的操作变量之间具有高度非线性和相互强偶联的关系;且传统的数据关联模型中变量相对较少、机理建模对原料的分析要求较高,对过程优化的响应不及时,也很难全面地描述工艺过程,所以建模的效果并不理想[9-15]。孔金生等[16]对催化裂化数据进行了预处理并建立了粗汽油终馏点的神经网络模型,4.7%的样本误差小于±1 ℃、98.3%的样本误差小于±2 ℃、样本均方差为0.7379 ℃、绝对误差的平均值为0.5779 ℃,结果证明该模型具有较高的预测能力。杨帆等[17]基于某石化企业的LIMS及DCS中的工业生产数据,利用GBDT模型预测汽油收率,模型预测准确率为98.9%,平均绝对误差为0.531%。张忠洋等[18]以某炼油厂催化裂化反应-再生系统为研究对象,用遗传算法优化了已建立的6-11-1结构的BP神经网络,成功将汽油产率预测均方误差从5.16%降低到4.92%。上述研究都是通过神经网络、遗传算法等人工智能算法对工业经验中已知的影响催化裂化产品收率的指标进行分析,并构建催化裂化汽油收率预测模型,实现相应的汽油产率预测。通过建立化工过程模型,基于数据挖掘技术,对重要指标的相关数据进行分析,寻找优化方案,最终实现催化裂化装置经济效益的提升。但是基于神经网络的预测模型的解释性较差,基于遗传算法的预测模型无法处理大规模复杂问题且其自身存在局部最优性。因此,笔者将使用主成分分析算法对数据进行降维,降低算法的计算开销,结合具有较好解释性的树类随机森林模型进行预测。
为了优化汽油精制处理过程,实现最大化经济效益,对装置运行积累的数据进行分析,利用随机森林回归模型进行预测,并在实际生产中指导生产,及时优化操作变量。笔者以霍尼韦尔(PHD)实时数据库及实验室信息管理系统(LIMS)数据库的数据为基础,基于改进主成分分析的随机森林回归PCA-RFR模型,对操作变量进行筛选,构建了汽油辛烷值损失预测模型。
1 数据预处理
1.1 数据格式统一
笔者使用的原始数据来自于中国石化上海高桥分公司催化裂化汽油精制脱硫装置的PHD实时数据库及LIMS实验数据库。通过PHD及LIMS数据库采集到原料、产品和催化剂等相关数据,其采集频率为2次/周。为了采集到足够多的数据,并保证实验的准确性和有效率,LIMS数据分别采集了从2017年4月至2019年9月和2019年10月至2020年5月2个时间段,共约3年。通过PHD数据库可采集到操作变量数据,第一时间段数据采集频次为3 min/次,第二时间段数据采集频次为6 min/次。原始数据包括7个原料性质、2个待生吸附剂性质、2个再生吸附剂性质、2个产品性质等不可操作变量以及另外354个操作变量(共计367个变量),将所有的数据按照时间戳降序排列,以方便系统化的数据处理和分析。再对数据进行如下处理:
(1)数据格式统一。第二个字段为Timestand类型,不符合Float类型,直接将此列删除。
(2)缺失数据填充。删除缺失率大于20%的数据列,对于缺失率小于20%的数据列,使用其前后2 h数据的平均值进行替代填充。
(3)噪声处理。根据工艺要求与操作经验,总结出原始数据变量的操作范围,删除不在该范围的数据。
(4)根据拉依达准则(3σ准则)去除异常值。3σ准则:对被测量变量进行等精度测量,得到x1,x2,……,xn,计算其算术平均值x及剩余误差vi=xi-x(i=1,2,…,n),利用按贝塞尔公式计算标准误差σ,若某个测量值xb的剩余误差vb(1≤b≤n)满足|vb|=|xb-x|>3σ,则认为xb是含有粗大误差值的坏值,应予剔除。贝塞尔公式如式(1)所示。

(1)
1.2 模型变量筛选
数据中含有354个操作变量,如果将所有操作变量都考虑进去,不但会增加计算的复杂度,并且由于样本数量太少,导致过拟合,从而影响模型准确性。由于炼油工艺过程的操作变量之间具有高度非线性和相互强偶联的关系,考虑采用改进PCA算法对处理后的数据进行降维,筛选出相关性较高的30个操作变量作为预测模型的输入,改进PCA算法执行过程如下:
(1)对数变换。传统的主成分分析是一种线性的降维方法,为了实现对高度非线性数据的高效处理,采用对数变化来改变数据的分布使其接近假设的模型[19]。设格式统一后的数据矩阵如式(2)所示。
X=(xij)n×p
(2)
令yij=lnxij,则对数变换后矩阵如式(3)所示。
Y=(yij)n×p
(3)
(2)数据标准化。为了消除样本不同属性具有不同量级的影响,需要对对数变换后的数据进行标准化处理,使结果值映射到[0~1]之间,转换公式如式(4)所示。
(4)
式中:X*为标准化后的数据,X为原始数据,Xmax为样本数据的最大值,Xmin为样本数据的最小值。
(3)协方差矩阵。协方差矩阵表示一组随机变量之间的两两相关性。根据标准化矩阵,计算其协方差矩阵。
(4)主成分特征值得分及其对应贡献率。对协方差矩阵进行奇异值分解求出所有的特征值得分,并从大到小排列。表1为所有特征值中排名前30的得分情况。

表1 排名前30主成分的特征值得分Table 1 The top 30 principal component characteristics
根据所有的主成分特征值的得分,求出所有主成分的特征值得分占比,以贡献率(Φ)表示,提取贡献率前30对应的主成分及其贡献率。前m个主成分的贡献率(Φ)如式(5)所示。
(5)
式中:λi为第i个主成分特征值的得分情况;m为1~30。
采用改进PCA算法对所有操作变量进行分析和筛选,得出与RON损失相关性较高的操作变量及其特征值得分和相应贡献率。如图1所示。

D-109,D-110,D-113,D-114,D-121,D-122,D-123,D-124,D-125,D-201,D-202 are the serial number of feed liquid storage tanks of S Zorb adsorption desulfurization unit.图1 主要操作变量及其贡献率和综合得分Fig.1 Main operating variables and their contribution rate and comprehensive score
2 模型构建
笔者采用改进主成分分析-随机森林回归算法PCA-RFR建模。改进PCA-RFR模型结构如图2所示,包含输入层、隐藏层、输出层。RFR从输入数据中随机抽样,并训练得到若干棵决策树,再将测试集输入模型中,由各决策树预测值的平均值决定最终的预测结果,模型的输出即为对汽油辛烷值损失的预测值。

图2 改进PCA-RFR模型结构示意图Fig.2 Improved structure diagram of PCA-RFR model
算法的执行步骤如下:
输入:筛选出的主要操作变量的数据。
Step 1:初始化RFR随机森林回归模型,建立训练集和测试集。
Step 2:从训练样本集S中每次随机取出m个样本点,得到n个子训练集。
Step 3:选择第j个变量和其取值s,作为切分变量和切分点,将每个子训练集D递归地划分为2个子区域D1和D2,构建二叉决策(回归)树。划分方法如式(6)~式(9)所示。
D1(j,s)=(x,y)∈D|A(x)≤s
(6)
D2(j,s)=(x,y)∈D|A(x)>s
(7)
c1=average(yi|xi∈D1(j,s))
(8)
c2=average(yi|xi∈D2(j,s))
(9)
式(8)~式(9)中:c1为D1的样本输出均值;c2为D2的样本输出均值。
Step 4:然后寻找最优的切分变量以及最优的切分点,选择使式(10)达到最小值的(j,s)。
(10)
Step 5:对2个子区域重复1和2步骤,直到满足停止条件。
Step 6:将输入空间划分为M个区域R1,R2,……,Rm,生成多棵CART回归树Tm,组成随机森林。划分方法如公式(11)所示。
(11)
Step 7:将测试集样本输入随机森林回归模型中,随机森林最终的预测结果即为所有CART回归树预测结果的均值。
3 结果与讨论
笔者所使用的数据共有450组,其中,2018年1月1日至2020年5月26日期间的315组数据作为训练集,2017年4月17日至12月29日期间的135组数据作为验证集。通过实验,分别获得笔者建立模型PCA-RFR与BP神经网络模型BP-NN和随机森林模型Random Forest在测试集上的评估标准值,如表2所示。
由表2可以发现,PCA-RFR模型预测的误差最小,准确率最高,且R2值接近1,表明该模型非常拟合训练数据。
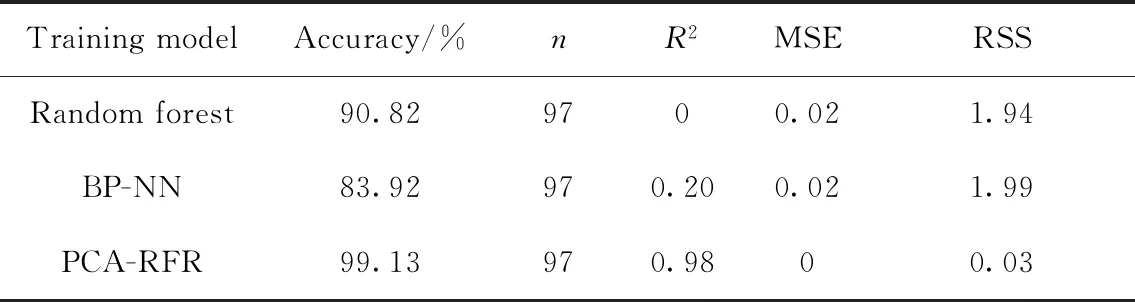
表2 3种模型的实验结果对比Table 2 The experimental results of the three models
在相同的测试集上,分别使用3种模型对汽油辛烷值损失进行预测,并将预测结果和实际数据进行比较,3种模型的汽油辛烷值损失预测值和实际值对比,如图3所示。由图3可以看出:BP神经网络模型中的整体预测值在实际值附近上下波动,对汽油辛烷值损失预测有一定的偏离,可以大致地拟合出汽油RON损失的变化趋势。随机森林模型对汽油RON损失预测较为平稳,大部分预测值与实际值偏差不大,但是模型的预测值变化幅度较小,无法对汽油RON损失的突然变化进行预测。改进PCA-RFR模型对汽油RON损失预测结果基本与实际值相符,且可以预测出汽油RON损失曲线的突变。对比3种模型对汽油RON损失的预测结果,改进PCA-RFR模型的预测更加准确。

图3 3种模型对汽油辛烷值损失预测值和实际值对比Fig.3 The predicted and actual octane loss values of three models(a)Back propagation-neural network (BP-NN);(b)Random forest;(c)Principal component analysis-random forest model (PCA-RFR)
根据3种训练模型样本的实际值和模型的预测值构建散点图,如图4所示。由图4可以看出:BP神经网络的回归样本呈区域集中,实际值与预测值差距较大;随机森林和改进PCA-RFR回归样本分布均匀,但后者的预测值与实际值更为接近。
最后,对训练模型中的450组样本中硫含量数据进行微调:原数据加上一个由random函数随机生成的0~1之间的数,将调整后的数据放入模型的数据库中,通过已建立的PCA-RFR汽油辛烷值预测模型训练新的数据,得出改变硫含量后的汽油RON损失预测,如图5所示。可以看出,笔者所建立的PCA-RFR预测模型在对操作变量进行优化的过程中,能够非常直观地展示汽油RON损失值的变化情况,及时为生产控制提供分析数据,有效地解决化工过程RON损失预测建模问题。

图5 硫含量变化后汽油辛烷值损失预测图Fig.5 Prediction chart of the octane loss after sulfur content change
优化过程中主要操作变量调整后,对应的汽油辛烷值损失和硫含量的相对值变化轨迹,如图6所示。图中,汽油辛烷值损失是由参数调整后模型的出的结果与原数据模型得出的结果做差得到的,硫含量的值也是调整后硫含量的值与原硫含量的值做差得到的。可以看出,硫含量变化与RON损失变化呈一定的线性相关性,部分点数值变化幅度过大,分析数据存在一定的波动,但仍在重复性标准要求范围之内。
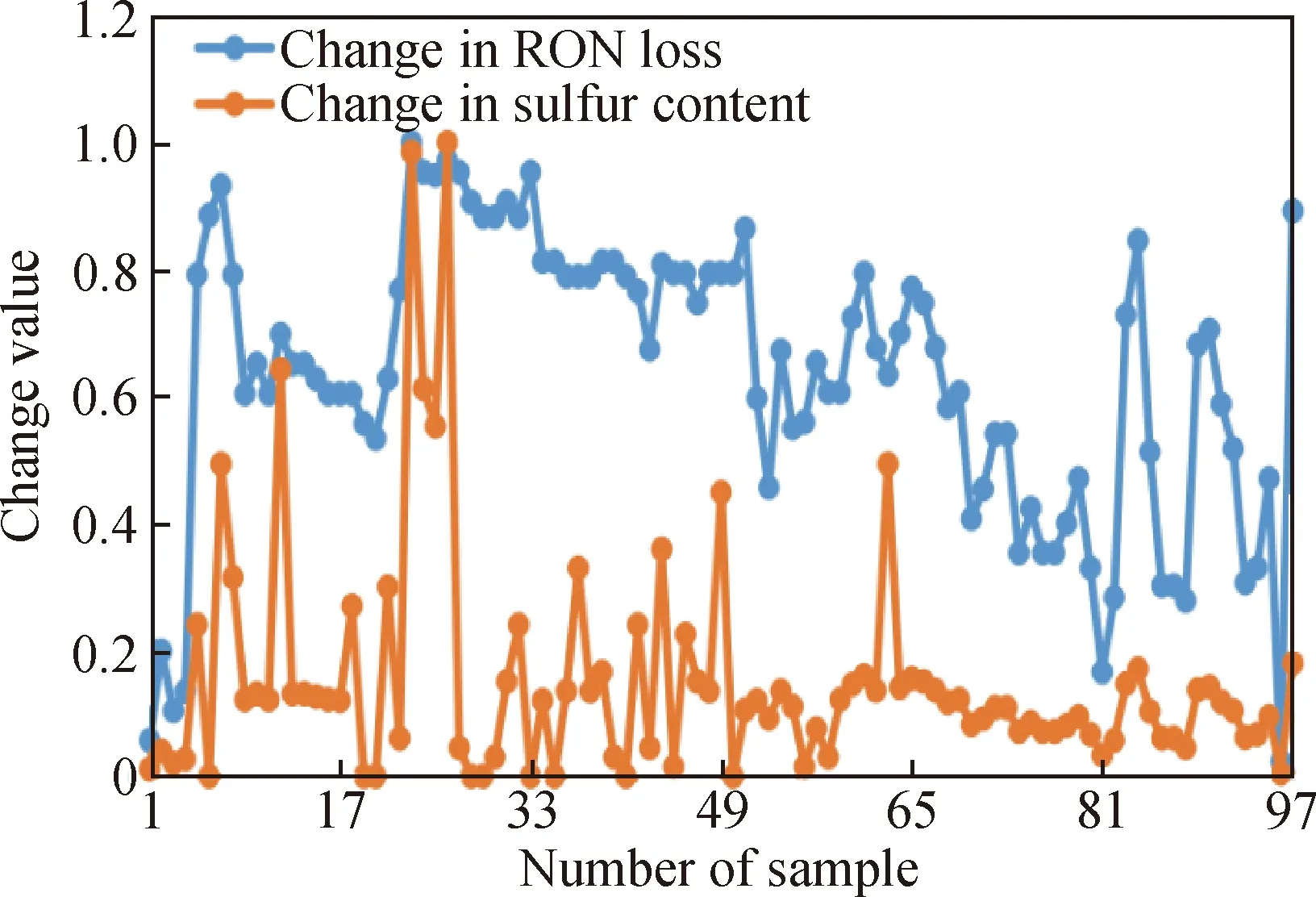
图6 汽油RON损失值与硫含量变化轨迹图Fig.6 Track diagram of the gasoline RON loss and sulfur content change
4 结 论
笔者基于PHD实时数据库及LIMS实验数据库,通过改进PCA算法,分析各操作变量与实际催化裂化汽油精制处理过程中汽油辛烷值损失的相关性,筛选出了30个潜在影响辛烷值损失的关键操作变量作为预测模型的输入,利用RFR模型预测催化裂化汽油辛烷值的损失,并将模型对汽油辛烷值损失的预测效果作为基准。结果表明,由改进PCA-RFR构建的汽油辛烷值损失预测模型预测结果的准确率为99.13%,R2为0.983,均方根误差为3.2169×10-4。模型对真实汽油辛烷值损失的拟合效果非常接近,有助于在实际生产中优化操作条件,减少辛烷值的损失,提高生产经济效益。开发高辛烷值汽油技术仍然是未来催化裂化发展的主题,下一步工作考虑采用NSGA-Ⅱ多目标参数优化算法[20],分析各个操作变量的支配强度Pareto等级和拥挤度,最终找到减少汽油辛烷值损失的Pareto最优解集。

