基于模拟退火法的能源隧道取热段最优化设计

刘佳欣，韩婵娟，蔡国庆

1）上海交通大学船舶海洋与建筑工程学院，上海200240；2）上海市公共建筑和基础设施数字化运维重点实验室，上海200240；3）北京交通大学土木建筑工程学院，北京100044

寒区隧道的冻害问题如衬砌开裂、洞门开裂、排水沟冻结和挂冰等，轻则影响隧道的正常运营，重则对隧道结构产生永久性的损害而使其报废．诱发冻害的原因主要有渗漏水、极端天气和冻胀作用等［1］．在严寒地区隧道工程中常采用双侧保温水沟和中心深埋水管等排水防冻措施，尽管能够有效防止隧道冻害，但不能完全避免其发生，隧道洞口排水沟仍会冻结一段时间．目前，常用的防治隧道冻害问题的方法有保温材料法、防排水法、防寒门法、空气幕法、阳光棚法、围岩注浆法和加热法等［2］．其中，加热法一般为电加热或者使用燃煤锅炉暖气加热，虽然能根除冻害问题，但经济效益不高且会造成环境污染．能源隧道作为从地层中提取浅层地温能给建构筑物供暖制冷的一项崭新的节能技术的具体应用，在防治寒区隧道冻害问题上具有很大前景．

能源隧道的核心是地源热泵技术，后者是利用地球表面浅层土壤中的浅层地温能作为冷（热）源，实现建筑物夏季制冷、冬季供暖的一种高效、环保节能技术，可有效缓解建筑能耗对化石燃料的依赖，促进节能减排［3］.地源热泵技术在中国有较好的适宜性［4］，目前，中国31个城市均有相关工程［5］.

2006年，奥地利学者BRANDL等［6］研发了能源土工布用于能源隧道中热交换管的铺设．NICHOLSON等［7-8］对伦敦横贯铁路工程进行了详细的能源隧道的系统设计，包括布置在隧道衬砌内埋管的管径、管间距、布置形式以及成本等参数的设计计算．2015年，利用地温能加热隧道洞口的水平埋管换热系统成功应用于日本的Nanaori-Toge隧道［9-10］．2016年，BARLA等［11］对意大利都灵地铁1号线能源隧道采热系统进行设计和优化，分析了能源隧道技术对周围环境影响的可持续性．2019年，COUSIN等［12］分析了隧道能源分段衬砌的能源性能和经济可行性，指出在进行合理分析和设计的前提下，能源隧道分段衬砌技术是建筑环境可再生能源供应的一项突破性技术．

中国对于能源地下结构的研究始于21世纪初．夏才初等［13］对能源地下结构的传热理论及设计方法进行了研究分析，得到了寒区隧道温度场解析解，与相关施工单位建成了一批能源地下结构的项目，其中包括内蒙古高速公路扎敦河能源隧道和博牙高速林场能源隧道［3］．张国柱等［14-16］考虑衬砌结构和热源的影响，建立了能源隧道取热段围岩的传热数学模型，通过数学物理方法，得到了寒区隧道轴向及径向温度分布理论解及取热段温度场解析解，并通过岩土热响应测试证明了模型的准确性．

本研究利用Comsol多物理场耦合有限元软件和Matlab数学软件，针对某严寒地区山岭隧道隧址的地层和气候条件建模，计算得到当地初始地层温度分布和洞口保温段所需供热量，选取最小取热段长度及对应的最优取热段位置，最后选取了3个换热管设计参数，分析其对传热特性的影响，并对不同参数下取热段长度及位置的选取进行对比．

1 模型概述

1.1 隧道信息

本研究的山岭隧道位于中国内蒙古卓资县，隧址区属中温带亚干旱蒙东区，日均温度分布请扫描论文页末右下角二维码查看图S1．年平均气温为4℃，最冷月平均气温为-15.9℃，最低气温为-38.2℃，最大冻结深度为246 cm．隧道全长为3 380 km，最大埋深为402 m，断面面积为143 m2，属于特大断面、特长隧道．隧道中部为单圆拱，跨度13.8 m，采用新奥法（new Austrian tunnelling method，NATM）开挖，复合式衬砌支护，拱顶初衬厚度350 mm，仰拱位置初衬厚度850 mm，二衬厚度500 mm．隧道中部位于弱风化大理岩中，围岩等级为Ⅲ级，埋深大于100 m．

为避免隧道出现局部冻结，本研究将气温低于0℃的时间定义为该隧道洞口段的一个标准供暖季．

1.2 有限元模型

本研究利用Comsol软件，建立针对能源隧道地源热泵型热交换系统的三维仰拱埋管传热模型，如图1．其中，衬砌围岩和换热管的传热过程应用固体传热和非等温管道流模块模拟，隧道内壁与洞内空气的换热利用热对流边界条件描述．隧道的具体材料参数见表1［17-18］.

表1 隧道材料参数［17-18］Table 1 List of material parameters［17-18］

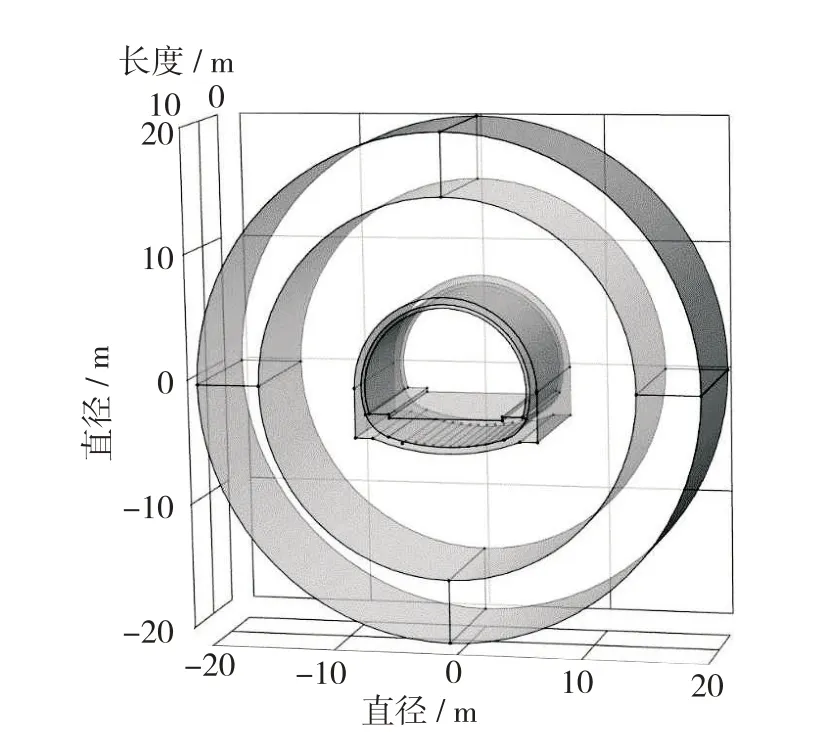
图1 仰拱埋管热交换系统能源隧道三维模型Fig.1 3D model of energy tunnel of heat transfer systemburied in inverted arch

2 取热段位置选取

隧道取热段位置的选择需要同时考虑保温段长度和取热段长度，鉴于工程实践中保温段长度是相对固定的，为了降低成本，取热段长度应尽量减小．

隧道取热段的热交换管利用循环介质与管外围岩的温差吸收围岩中的地温能，当管内循环介质入口温度一定时，隧道围岩地温越高，热交换管换热效率越高，提取的地温能越多，所需取热段长度越短．而当气象条件和工程条件一定时，隧道围岩地温主要受隧道埋深的影响，即隧道埋深越深，地温越高．此外，隧道取热段距洞口越远，围岩与洞内空气对流换热系数越小，散热量越小，取热能力则越强．因此，隧道取热段应布置在平均地温尽量大、距洞口尽量远的位置，并且综合考虑循环介质的热损耗量，以减少取热段长度．

本研究中，隧道取热段长度是根据地温与埋深的关系，利用隧道取热段每延米取热量对隧道取热段长度积分满足保温段所需总供热量的关系而获得的．因此，取热段长度的确定需要：①获得隧道轴线位置的年均温度分布曲线；②明确地温与换热量的数学关系；③计算隧道洞口保温段所需供热量以及传输过程中的热量损耗．

2.1 隧道轴线年温度分布曲线

土壤温度变化主要受气温变化影响，其日振幅随着深度的增加而减小，相位也逐渐落后．如果将土壤温度振幅小于0.1℃的土层视为恒温层，则恒温层深度H［19］可表示为

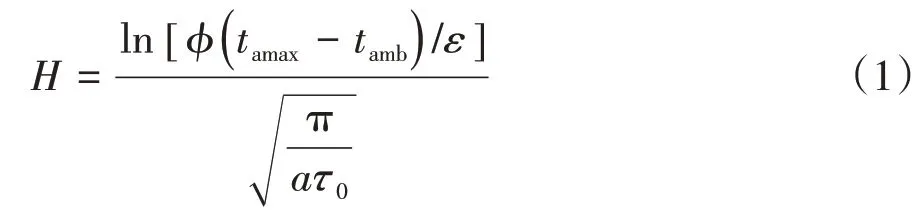
其中，φ为常数，本研究取0.51；tamax为年最高日均气温，本研究取23.9℃；tamb为年均气温，本研究取4℃；ε为恒温层温度振幅，本研究取0.1℃；a为土壤热扩散系数，本研究取8.88×10-7m2·s-1；τ0为年周期时间，本研究取365 d．

由式（1）可得，本研究隧址区恒温层埋深约在18 m以下，恒温层温度为7℃．结合隧道纵断面图可得，隧道取热段最大埋深402 m，最小埋深160 m，远大于恒温层埋深．

为了进一步确定地层温度，本研究首先采用数值计算的方法［20］得到了隧道贯通前后轴线纵断面温度分布情况（图2）．其中，里程为张家口至呼和浩特方向．该温度分布充分考虑了沿线的地层分层和水平围岩性质不均的影响，忽略了断层的影响．然后，从断面分布图中提取隧道沿线的温度数据，绘制出隧道轴线位置地层年均温度分布曲线，如图3．

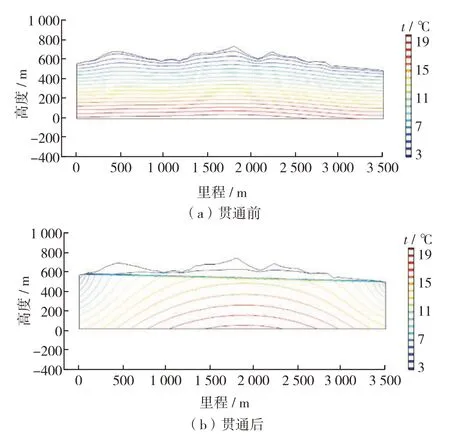
图2 隧道纵断面年均温度等温线图Fig.2 Average annual temperature isotherm of tunnel longitudinal section

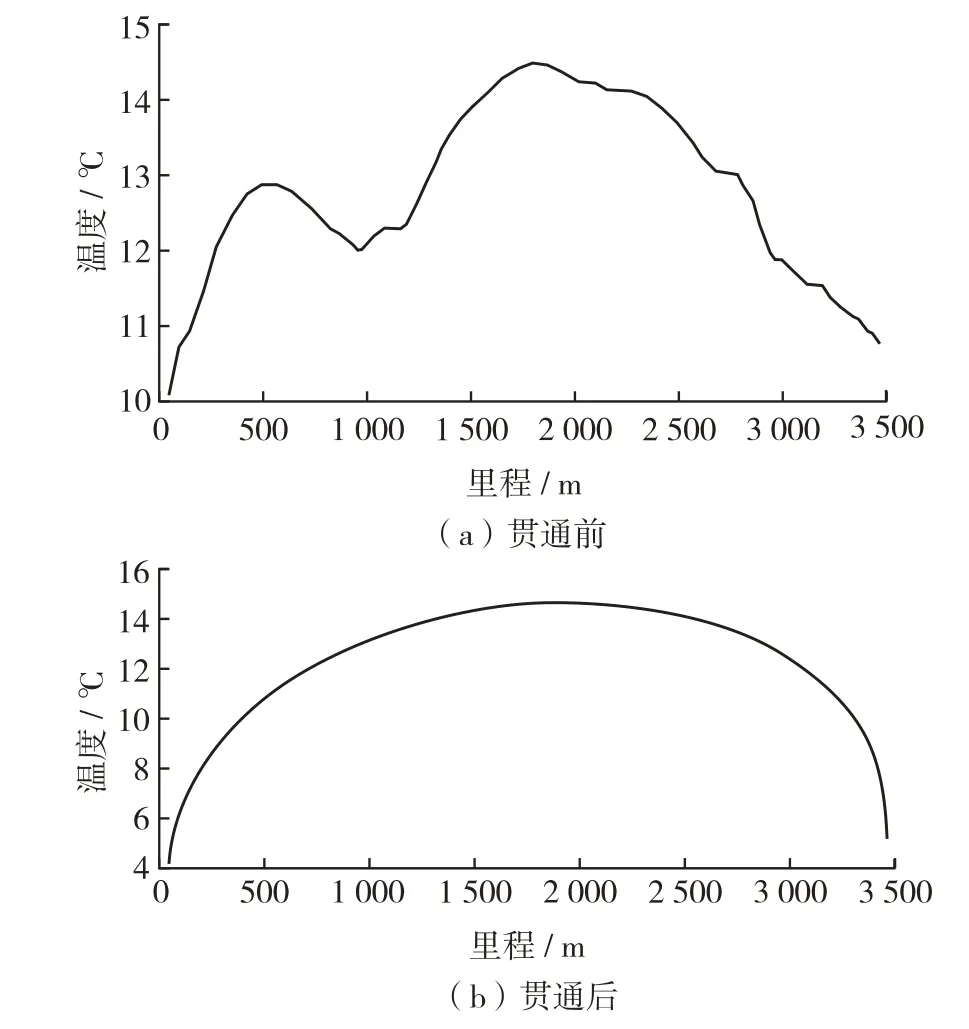
图3 隧道轴线位置地层年均温度分布曲线Fig.3 Average annual temperature distribution along tunnel axis

2.2 初始地温对取热效率的影响

为了研究初始地温对隧道地源热泵型内埋管换热系统取热效率的影响，本研究依次计算围岩地温为3.5、7.0、10.5和14.0℃时的取热功率．

隧道内埋管换热系统的取热功率可用一个供暖季内每隧道延米的内埋管换热系统换热量Q代表，计算公式为

其中，cp为水的恒压热容，取4.2×103J·kg-1·℃-1；ρ为水的密度，取1 000 kg·m-3；q为管内流体流量，q=upA；up为管内循环介质流速；A为管道截面积；Δt为管内流体进出口温差．

标准供暖季隧道每延米平均取热功率随地温变化曲线见图4.由图4可见，初始地层温度对取热量有显著影响，标准供暖季内平均取热功率Qˉ与地温θg基本满足线性关系，即Qˉ=5.8θg+19.8．相对于14℃的缺省值，初始地温为3.5、7.0和10.5℃时，隧道取热段取热功率分别减少了60.3%、23.1%和19.2%．因此，在工程实践中，考虑到隧道埋深越深，围岩地温越高，隧道围岩取热量将越大，热交换管应尽量布置在隧道埋深较深的部位．

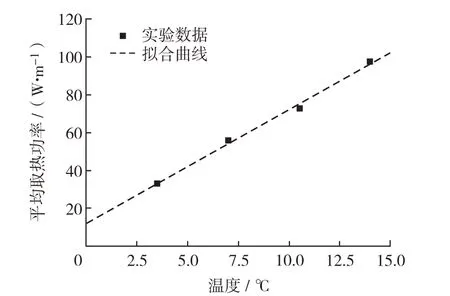
图4 标准供暖季每隧道延米平均取热功率随地温变化曲线Fig.4 Variation curve of average heating power per linear meter in standard heating season

2.3 洞口保温段所需供热量计算

洞口段冬季保暖所需供热量由隧道每延米所需供热量、供热段隧道长度和热量损耗决定．

2.3.1 洞口段每隧道延米热负荷

由于隧道洞内和地面空气温度是决定隧道结构温度的主要因素，可以假设洞口段每隧道延米防冻保温所需热负荷q(t)随空气温度以年为周期按正弦函数变化，总热负荷［3］，为

其中，qmax为隧道防冻保温所需的最大供热负荷；φ为负温度年曲线与正弦函数之间的相位差；t1和t2为系统工作起止时间．

本研究中，首先将空气温度低于零度的时间作为工作时间，即t1=296 d，t2=455 d．为获得最大供热负荷qmax，将换热管简化为热源，采用不同的热功率来分析热交换管对双侧保温水沟、中心深埋水管和初衬的加热效果．然后，以双侧保温水沟、深埋中心水管内平均水温及初衬测点位置供暖季温度不出现负温为目标，计算得到每延米隧道保温段所需供热负荷．

图5为隧道洞口段横断面二维平面数值模型．该模型综合考虑了换热管与围岩的换热过程，以及洞壁与洞内空气的对流换热过程．

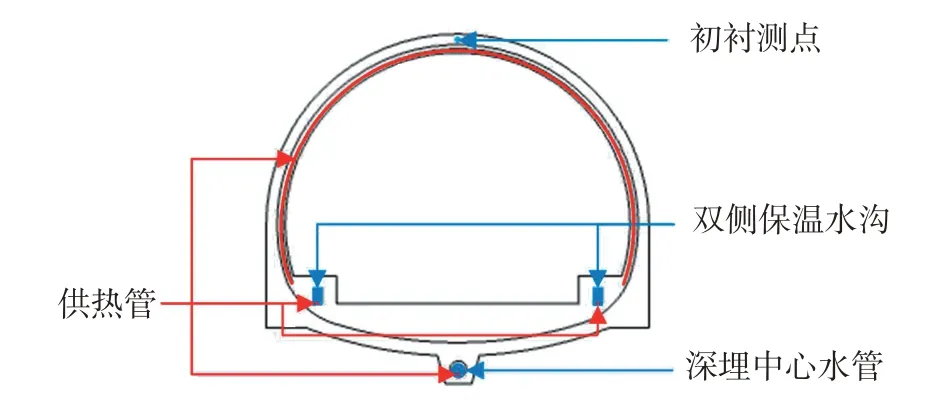
图5 隧道洞口段横断面二维平面数值模型Fig.5 2D plane strain finite element model of tunnel portal section

供暖季隧道每延米不同加热功率下测点温度变化曲线见图6.由图6（a）可见，当隧道双侧排水沟内换热管的供热功率达到15 W每延米时，供暖季内不再有结冰的危险．由图6（b）和图6（c）可见，当供热功率分别为10 W和25 W时，深埋水管和衬砌排水系统不再有结冰风险．因此，为了避免隧道保温段的结冰风险，所需总供热量应该大于三者所需供热功率之和，即50 W每延米．

图6 供暖季每隧道延米不同加热功率下测点温度变化曲线Fig.6 Temperature variation curves of measuring points under different heating powers per linear meter in heating season

2.3.2 保温段基础长度

隧道保温段设置长度L(保温段)可由HITOSHI Kurokawa［21］经验公式计算求得，

其中，θ为洞口最冷月的月平均温度，本研究隧道取-15.9℃．

由式（4）可得，隧道保温段长度L=823.6 m．叶朝良等［22］统计了中国35座季节性冻土隧道温度场的实测结果，指出HITOSHI Kurokawa经验公式得到的结果普遍小于实际保温段设置长度，可将其视为保温段长度设置下限．因此，本研究的隧道取保温段长度为824 m．

2.3.3 隧道热量损耗

隧道取热段与保温段之间由分、集水管路相连接，由于管内流体与洞内空气存在温差，管内流体的热量损耗不可避免，分、集水管路越短，其外侧包裹的保温材料隔热性能越好，则管内流体的热量损耗越少，越有利于系统能效的提高．

热量损耗Δq()t可根据管壁内外侧的温差计算为

其中，p为管内壁周长，对于管径为50 cm的分、集水管，本研究取157 cm；λ1为保温材料导热系数，本研究取0.03 W·m-2·K-1；Lp为共同沟内分、集水管低温耗热段总长，本研究取两倍保温段长度1 648 m；Δt为管内循环介质与管内壁平均温度之差，本研究取平均温差4℃．由此，可计得整个供热季内分、集水管耗热量为310.3 W（即保温段供热量为0.2 W每延米）．

综上所述，隧道洞口保温段1个供暖季内所需热负荷Qneed为50.2 W每延米．

2.4 取热段选取

模拟退火算法是一种基于蒙特卡罗迭代求解法的启发式全局优化算法．退火过程由衰减控制参数、衰减因子和控制参数下的最大迭代次数和停止条件（控制参数t的终值）控制．由图2和图3可知，隧道埋深沿隧道轴线方向依地形呈不规则变化，地温沿隧道轴线也呈现出不规则非对称分布的情况．对于具有局部极值的初始地温曲线，使用普通的搜索算法通常会使结果跳入局部极值的“陷阱”中，从而得到局部最优解，而模拟退火算法能够有效避免此类情况发生．因此，本研究采用模拟退火算法实现隧道最优取热段起始位置及最小取热段长度的求解，计算流程图请扫描论文末右下角二维码查看图S2．

由2.2节可知，标准供暖季内平均取热功率Qˉ(x)与地温Tg(x)满足Qˉ(x)=5.8Tg(x)+19.8．

由于取热段位置不能覆盖保温段位置，取热段起始位置的取值范围D为824～2 556 m．在寻找最优取热段位置过程中，目标函数为

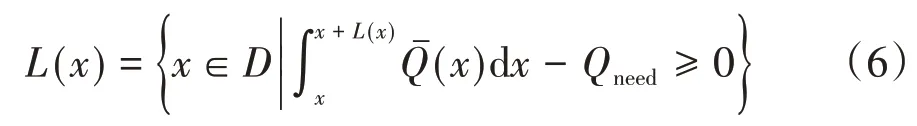
由式（6）所得最优取热段位置和长度如图7及图8.其中，取热段长度最小为796 m，取热段起始位置距洞口1 326 m，与两侧保温段末端距离分别为502 m及434 m．

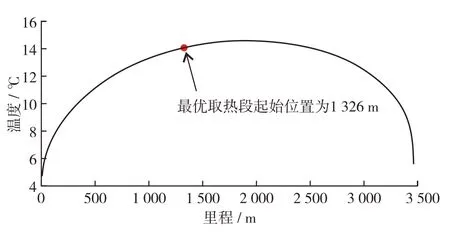
图7 模拟退火算法找到的最优取热段起始位置Fig.7 The optimal starting position of the heat extraction section found by simulated annealing algorithm

图8 取热段及保温段位置示意图Fig.8 Schematic diagram of heat extraction section and heat preservation section

3 最优化设计影响因素分析

隧道内埋管换热器的取热效率及取热段位置的选择除了受初始地温和当地气候等自然条件影响外，还受一些可控因素的影响，如换热管入口水温、管内流体流速及管间距等．本研究拟通过对上述可控因素开展敏感性分析，厘清其对取热效率及取热段位置选择的影响规律．试验方案如表2．

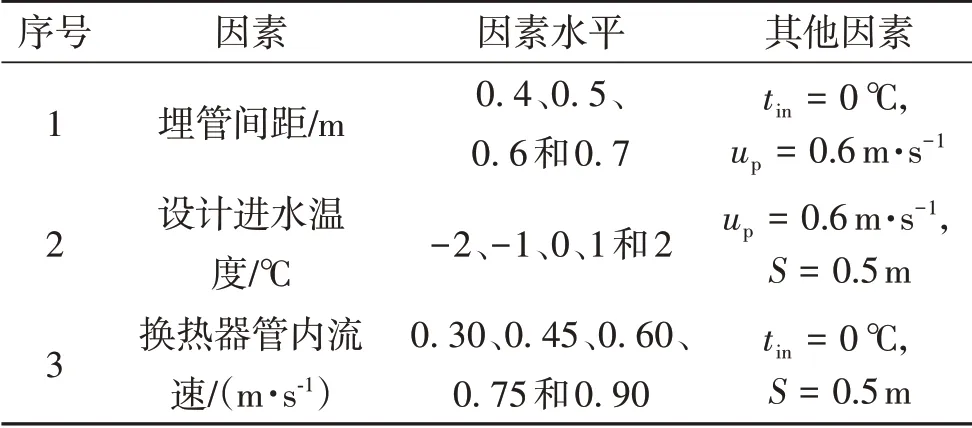
表2 试验方案1）Table 2 Test scheme

3.1 热交换管间距

为了分析不同埋管间距S对取热功率和取热段设计的影响，本研究中S分别取0.4、0.5、0.6和0.7 m，对应仰拱埋管系统的总管长分别为226.14、194.78、162.16和146.49 m．根据《地源热泵系统工程技术规范》［23］，埋管选用公称外径为25 cm聚乙烯管，壁厚取2.3 mm．不同的埋管间距下热交换管的几何模型如图9．标准供暖季不同设计参数下取热功率如图10．相对于S=0.5 m，S=0.4、0.6和0.7 m时，总管长变化为16.1%、-16.7%和-24.8%，而取热功率变化仅为0.14%、-2.20%和-2.75%．因此，考虑到减小埋管间距（增大埋管长度）会增加安装成本，但是系统取热量变化不大，当埋管间距从0.4 m增至0.7 m时，取热段最小长度仅减少了约2%，在工程实践中，最优的地埋管间距应取0.5～0.6 m．

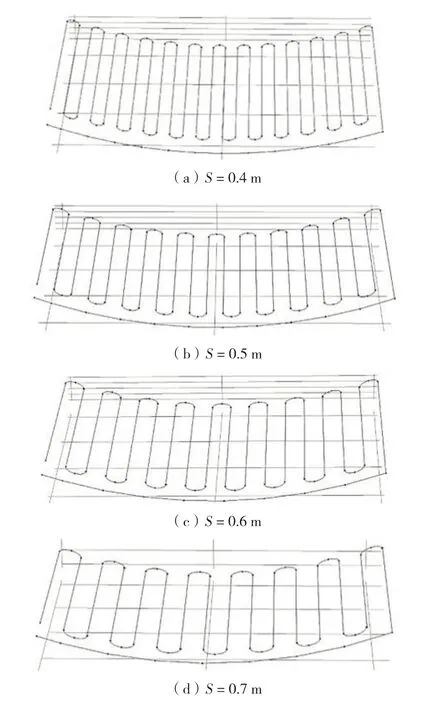
图9 不同间距隧道取热段内埋管路布置Fig.9 Layout of buried pipelines in heat extraction sections of tunnels with different spacing

此外，值得注意的是，对于同一个最小取热段长度，多次模拟会得到多个临近的取热段起始位置．例如，在S=0.5 m时，对于最小取热段长度796 m，取热段起始位置可取1 329～1 332 m.这意味着一定范围内，工程中可以灵活选择起始位置，施工位置的偏差对取热量的结果影响不大．

3.2 设计进水温度

《地源热泵系统工程技术规范》［23］提到，内埋管换热器中传热介质的平均温度通常取-2～5℃，且设计进口水温与平均水温在换热时应基本相同．据此，本研究选取5个进水口温度-2、-1、0、1和2℃来分析其对取热量的影响．

由图10（b）可知，对于不同的进水温度，取热功率基本与设计进水温度呈线性关系，设计进水温度越低，取热功率越高，且这种差别在整个供暖季的取热过程中都基本保持恒定．

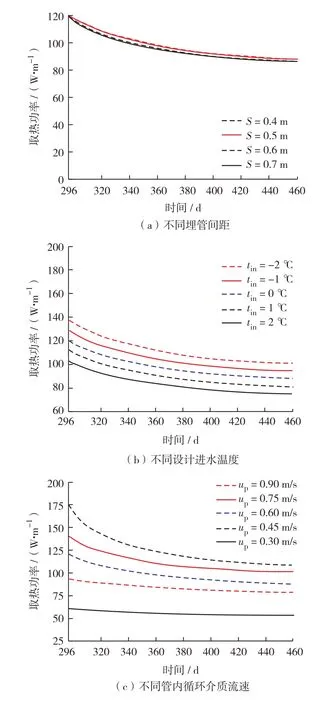
图10 标准供暖季不同设计参数下取热功率随时间变化曲线Fig.10 Heat extraction power of different buried pipe spacing in standard heating season

不同设计参数下标准供暖季隧道取热段最优长度及位置见图11.由图11可见，相对于缺省值tin=0℃时的取热段长度，tin=-2、-1、1和2℃对应的取热段长度分别变化了-12.3%、-6.4%、8.2%和16.8%，设计进水温度与最优取热段长度也基本线性相关．另一方面，提高设计进水温度，会增加热泵系统运行成本和循环介质传输过程中的热量损耗，随之而来的过高的取热功率也不利于围岩温度场的恢复，因此应该限制最大进水温度与围岩温度差．综上，在工程实践中，设计进水温度的选取应兼顾系统能效和环境效应，在满足上述要求的范围内越低越好．

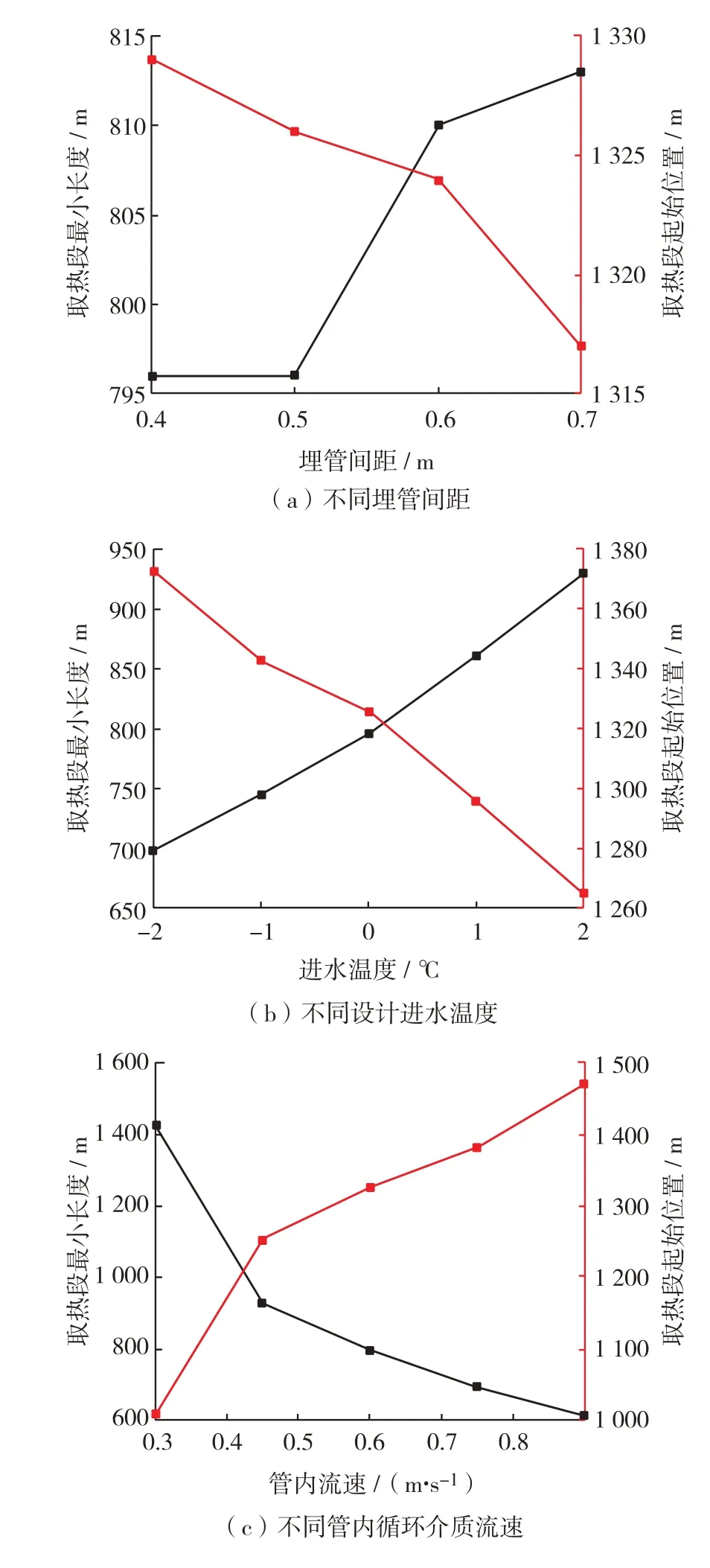
图11 不同设计参数下标准供暖季隧道取热段最优长度及位置Fig.11 Optimal length and position of heat extraction sections of tunnels in standard heating season under different design parameters

3.3 管内循环介质流速

《地源热泵系统工程技术规范》［23］中规定，为保证系统及时排气以及加强换热对循环介质最小流速的要求，双U形埋管的换热器管内循环介质流速不宜小于0.4 m·s-1．本研究分别选取了流速0.30、0.45、0.60、0.75和0.90 m·s-1，分析其对换热效率和取热段设计的影响．

标准供暖季不同管内循环介质流速取热功率和取热段最优长度及位置见图10（c）和图11（c）．结果显示，适当增大流速能够提高换热效率，改善系统性能，但到供暖季后期取热量差异减小．并且，增大管内传热介质流速也有利于减小取热段长度，相对于缺省值up=0.6 m·s-1，管内流速分别为0.30、0.45、0.75和0.90 m·s-1时，最小取热段长度分别改变了79.4%、16.8%、-12.6%和-22.7%．因此，能源隧道内埋管换热系统也应设置最小管内循环介质流速，且在满足管内水压限值的前提下，流速越大越好，推荐取值为0.5～0.6 m·s-1．

相对于本研究的间歇工作状态，相关研究［24］表明，连续工作状态下流速与换热效率的规律相反，这是由于循环水与围岩之间的热交换不充分，过高流速反而不利于换热效率的提高．

4结论

针对寒区能源隧道，采用数值模拟和模拟退火算法，计算了某严寒地区隧道区间的最优取热段位置及长度，分析了埋管间距、设计进水温度和管内循环介质流速对取热段换热效率及取热段位置选取的影响．可知：

1）埋管换热器取热功率与埋管间距和进水温度呈负相关，与管内循环介质流速呈正相关．减小埋管间距会增加系统安装成本，但取热量变化不大，较大的埋管间距更利于实现系统的经济性．取热功率与设计进水温度呈线性关系．

2）相比换热功率，取热段长度与上述因素的关系呈现相反的规律．减小埋管间距、降低设计进水温度以及增大管内循环介质流速都有利于取热段长度的减小和成本降低，但是更小的取热段长度意味着取热段起始位置距离洞口位置更深．此外，对于某一取热段长度，起始位置在数米范围内的偏差基本不会影响总的取热量．

3）本研究提出的基于模拟退火算法和数值模拟的能源隧道取热段最优化设计方法，可以有效指导能源隧道的设计．但是，鉴于在实际工程中，隧道土层存在纵向和横向上的不均匀分布、断层和裂隙的情况，以及不同土壤的传热性质具有差异性，获得精确的沿隧道纵断面的温度分布较为困难．因此，为了确保使用模拟退火算法求解最优取热段位置及长度的精确性，当隧道洞身位置地初始地温分布和土层的传热性质能够较为容易地确定时，该方法具有良好的实用价值．