基于Fluent的柔性玻璃新型成型工艺
曾启珉,刘 泉
(北京信息科技大学 机电工程学院,北京 100192)
0 引言
柔性玻璃是一种可弯曲超薄玻璃板,厚度在0.02~0.1 mm之间。其因具有柔韧、厚度极薄、可弯曲等特点,极具应用价值,应用范围广泛[1]。近年来,三星、华为和柔宇等国内外手机厂商已经利用柔性玻璃材料先后推出各自第二代折叠屏手机,推动了近十年来手机外观方面的重大改变。
柔性玻璃制备的核心专利基本掌握在国外的相关公司手中,如美国康宁公司的溢流下拉法、日本旭硝子公司的浮法玻璃和德国肖特公司的狭缝下拉法。我国的相关研发工作起步较晚,但也取得了较快发展。2018 年,我国使用锡液浮法生产出当时世界最薄的0.12 mm超薄玻璃。2020年生产出的0.03 mm超薄玻璃,可以实现产品连续20 万次弯折不破损,弯折半径小于1.5 mm,在锡液浮法领域已经达到世界领先的水平,打破了长久以来国际社会对我国的技术封锁。
目前较为成熟的电子柔性玻璃制备方法是溢流下拉法,这种方法生产出来的玻璃具有更好的平整度和平滑度,易于拉制更薄的玻璃板,也更容易控制玻璃带的温度[2]。该方法首先将熔融态玻璃液通过管道流入溢流槽内,当其填满溢流槽后,自溢流槽顶端流出,然后因为重力作用,沿着溢流砖外沿流下,最后在底部汇合形成玻璃带。根据现有可查询到的数据,目前该方法可生产的玻璃厚度为25~100 μm,弯曲半径小于2 mm,已经应用在三星折叠屏手机上。相较于已经成熟使用多年的浮法工艺和溢流法工艺,狭缝下拉法属于较新的领域,国内目前只有河北省沙河玻璃技术研究院的相关团队在进行研发。
随着市场对超薄玻璃需求的增加,超薄玻璃的生产厂商也面临着更高挑战:既要克服长久以来玻璃生产过程中良品率偏低的问题,又要解决成品可折弯半径的控制及柔性玻璃脆性大、易破碎的问题。因此本文基于已有的柔性玻璃制备方法,提出一种新型成型工艺,并利用计算流体力学仿真软件Fluent 进行相关的建模和计算。
1 新工艺设计
1.1 技术原理
本文提出的新型下拉法是一种在兼顾溢流下拉法优点的同时,可以对玻璃液的厚度进行实时调整的工艺。图1为新型下拉法工艺示意图。玻璃液入口阶段,采用双溢流槽结构,即左右两侧均配置一个溢流槽。通过左右两侧溢流槽流出的玻璃液,经过溢流槽外的斜坡,流入楔形板与溢流槽外斜坡之间的狭缝中。楔形板两侧的玻璃液最终在楔形板的尖部汇合,再一同依靠重力向下流出。
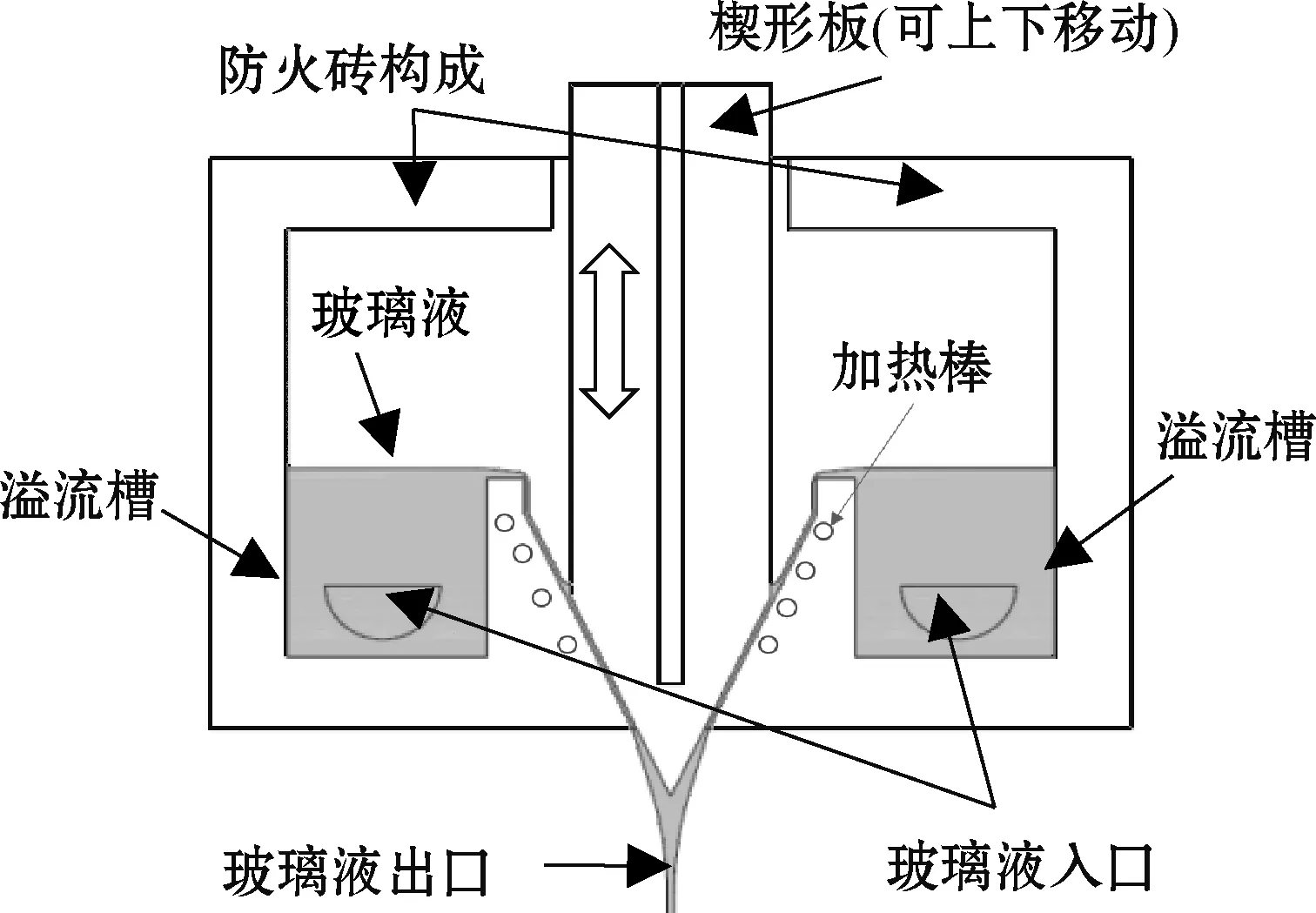
图1 新型下拉法工艺示意图
由于溢流下拉法工艺出口难以做到流量恒定,因此无法很好地控制玻璃板厚度的一致性,本设计针对这一缺点进行了改进。通过研究玻璃液溢流槽出口台阶溢出分布,对相关参数进行调整后,可以使得玻璃液在溢流槽出口台阶上表面均匀溢出。同时,在最终出口处增加一块楔形板,可以使出口处的玻璃液持续稳定地输出。而且也继承了狭缝下拉工艺的优点:整体设备体积不大,生产成本不高。
1.2 影响玻璃成型的因素
溢流下拉法会受到溢流槽设计参数、入口玻璃液流速与粘度、溢流槽温度分布等影响;狭缝下拉法会受到液面高度(液压)和铂金漏板设计参数等影响[3-4]。参考以上影响因素,列出新式下拉法中可能影响玻璃成型的因素。
1)溢流槽的设计参数。溢流槽是新式下拉法的重要机构,需要深入探究其中各种因素的影响。溢流槽结构如图2所示。主要参数为溢流槽上倾角α、下倾角θ、槽长L以及槽深h。同时将出口平均分为8个区域,分别进行研究,每个区域长度为s。参照目前使用的溢流下拉法工艺,其溢流槽内都有一定的倾斜角度,因此新型下拉法中也采用类似的具有上下倾角的溢流槽。
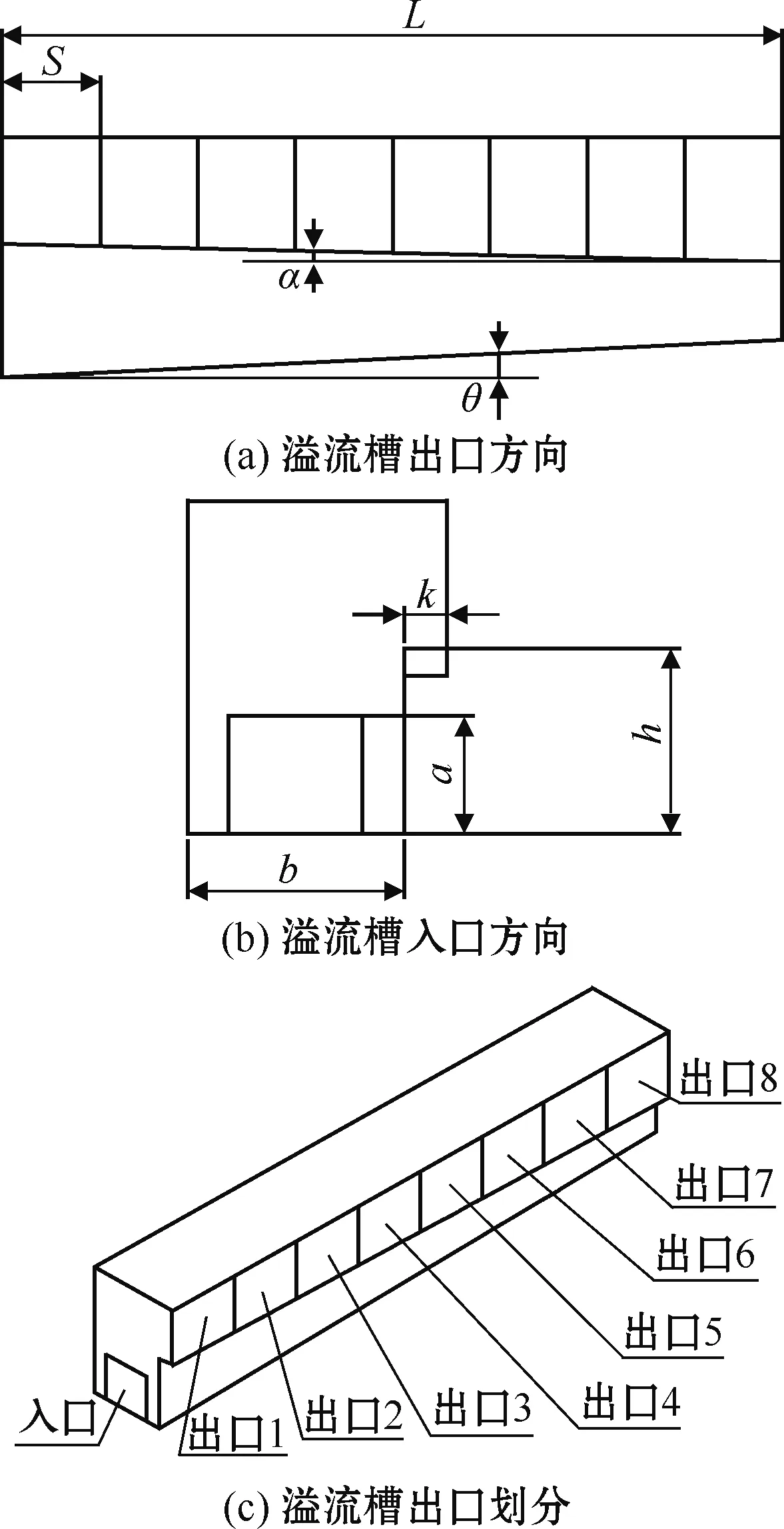
图2 溢流槽结构
2)玻璃液入口速度。在生产中,控制玻璃液入口速度是一种简单直观的办法。入口速度的大小直接决定了最终柔性玻璃的成品质量与物理属性。
3)玻璃液粘度。玻璃液因具有较大的粘度,所以在溢流槽中的自由流动会受到很大的阻碍。
4)楔形板设计参数。如图3所示,楔形板设计参数包括铂楔形板宽度d1、狭缝宽度d、狭缝长度D、溢流槽外斜坡倾角γ。其中狭缝宽度的大小将直接影响到最终柔性玻璃的成品质量。

图3 楔形板
1.3 仿真数学模型
1.3.1 前提假设
由于在柔性玻璃实际加工生产中,整体模型非常复杂,因此在使用计算机数值模拟仿真时需要对其进行简化,突出其主要特征,忽略其次要特征,这样既可以大大降低建模的难度,也会减少仿真运算的时间,提高科研效率。在本次实验中,使用Fluent软件来对新式下拉法进行相关模拟。
对相关物理性质进行如下假设:
1)熔融态玻璃液是一种牛顿流体,无法被压缩。
2)熔融态玻璃液的粘度只随温度变化。
3)熔融态玻璃液的密度、比热容、导热系数、表面张力与接触角不随温度的变化而改变。
4)假设在玻璃生产过程中所有环节均达到理想状态,不会出现包括气泡、条纹、结晶、杂质等在内的工艺缺陷问题。
5)玻璃液属于定常流动,并且是稳态传热。
1.3.2 粘性流体运动
粘性流体的运动遵循质量、动量、能量守恒定律,可以利用连续性方程、动量和能量方程来表示[3]。
1)连续性方程。连续性方程对应质量守恒定律,前者是后者的数学描述[4]。对于一个系统,流体流经一个空间位置固定的无穷小微团,其流入的质量和流出的质量相等。定义净流出量为正,则:
x方向的净流出量为
(1)
y方向的净流出量为
(2)
z方向的净流出量为
(3)
式中:u、v、w分别为流动速度在x、y、z方向上的分量;ρ为流体密度。
流出微团的净质量流量为
(4)
单位时间微团内质量增加值为
(5)
根据质量守恒定律,得到:
(6)
即:
(7)
或:
(8)
即:
(9)

2)动量守恒方程。动量方程对应牛顿第二定律,前者是后者的数学描述。对于系统中的运动流体微团,有f=ma,f为作用于微团上的力,m为质量,a为加速度。该向量关系式能够沿x、y、z轴的3个标量建立关系式,即:
x方向动量方程:
(10)
y方向动量方程:
(11)
z方向动量方程:
(12)
式中:η为粘性系数;p为静压;fx、fy、fz分别为x、y、z方向流体微团上的体积力的分量。
3)能量守恒方程。能量方程对应能量守恒定律,前者是后者的物理描述。对于系统的流体微团,微团内能量的随时间的变化率等于外力对微团做功的功率和单位时间进入微团的净热流量之和,即:
(13)

2 仿真
2.1 玻璃属性
本文使用的玻璃液参考德国肖特公司生产的一种无碱硼铝硅酸盐玻璃,主要成分和物理性质如表1所示[6]。

表1 本次实验玻璃在不同温度下的物理性质
2.2 仿真设置
为了避免模型结构过多造成计算上的误差以及节省计算时间、提高效率,本文主要仿真溢流槽内流体可流动的部分,忽略入口流道、溢流槽溢出后的部分。参照溢流下拉法工艺中的溢流槽[7-8],具体形状如图2所示,入口正方形边长a为160 mm,槽宽b为260 mm,槽深h为250 mm,槽长L为2 000 mm,出口台阶宽度k为50 mm。出口划分为8组,每组长度s为250 mm。
本次模型采用六面体网格,计算中网格与流动方向接近正交,其网格划分快捷、数值扩散较低,最主要是形状规则,计算速度快。检查网格数量为240 400,设置网格平均边长为0.01 mm,最大边长为0.015 mm。
在Fluent中进行如下设置:选择压力基求解器,选择瞬态模型来进行动态仿真,选择绝对速度,考虑重力,开启多相流流体体积(volume of fluid,VOF)模型,选择VOF隐式(Implicit)算法,选择层流模型。设置气相使用默认air参数,液相为熔融态玻璃液,设置液相之间表面张力为0.32 N/m。设置出口为压力型出口,表压为0。选择壁面为固定壁面,无滑移,接触角为56°。选择压力—速度耦合算法SIMPLEC。压力插值方案选择PRESTO!,空间离散方法均选择Second Order Upwind(二阶迎风式),时间离散格式选择Second Order Implicit(二阶隐式)。求解初始化后,设置残差为10-5时默认收敛,计算结束[9-10]。
2.3 仿真参数
通过调整下倾角θ和上倾角α使得溢流槽不论在距离入口多远的距离,都可以通过重力因素获得理想的压力差,从而稳定地溢出。根据不同的角度组合设计了4种方案,具体参数如表2所示,入口流速为0.004 m/s,玻璃液粘度为3 500 Pa·s。
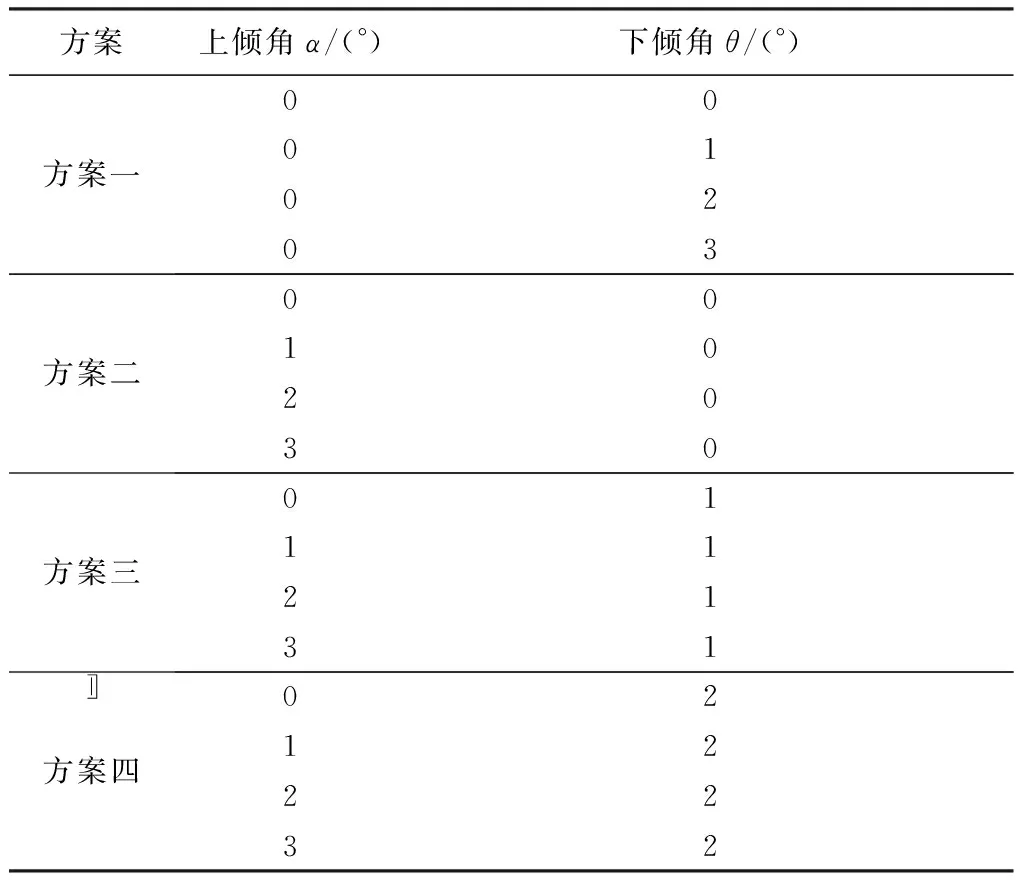
表2 不同的角度组合设计
2.4 仿真情况
在进行相关参数设置后,利用Fluent软件开始仿真,最终得到各方案的仿真溢流槽玻璃液溢流情况、出口溢流质量分布云图、出口流速分布云图及入口对称面流速矢量图,共64张。图4所示为其中一种组合倾角(上倾角为1°,下倾角为2°)模拟溢流的仿真图,通过对比每一种组合倾角的仿真图和仿真数据,来进行相关分析。
3 结果与分析
3.1 不同组合倾角模拟溢流质量分布
图5是4种方案的溢流质量与距离出口远近分布的关系图,横坐标为出口到入口的距离,纵坐标为对应位置的溢流质量。图5(a)展示了上倾角为0°时不同下倾角对溢流槽出口台阶面溢流质量的影响。可以初步看出,玻璃液溢流质量受不同下倾角的影响不大。这是由于玻璃液具有粘度较大的属性,流入溢流槽后会在入口处产生堆积,而向远端蔓延得较为缓慢。图5(b)、(c)、(d)中分别展示了下倾角为0°、1°、2°时不同上倾角对溢流槽出口台阶面溢流质量的影响。通过对比3张图中同一上倾角的曲线,可以看出其溢流质量分布大致相同。
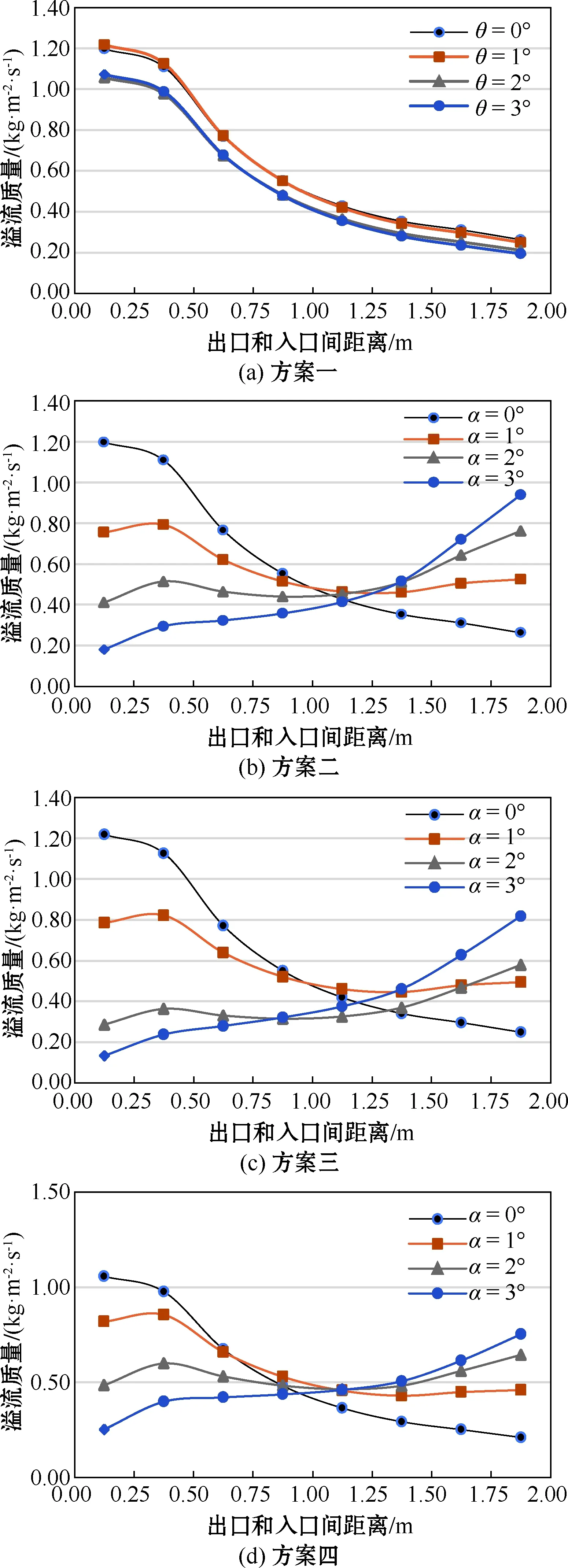
图5 各种方案的溢流质量分布
3.2 不同组合倾角模拟出口速度分布
图6是各种方案的溢流质量与距离出口远近分布的关系图,横坐标为出口和入口间距离,纵坐标为对应位置的出口速度。图6(a)展示了上倾角为0°时不同下倾角对溢流槽出口速度的影响。可以初步看出,玻璃液出口速度受不同下倾角的影响不大,同图5(a)得到的结论相同。图6(b)、(c)、(d)分别展示了下倾角为0°、1°、2°时不同上倾角对溢流槽出口速度的影响。通过对比3张图中同一上倾角的曲线,可以看出其出口速度分布大致相同。

图6 各种方案的出口速度分布
3.3 不同组合倾角模拟结果分析
为了更好地对比不同组合倾角出口速度和溢流质量的均匀程度,引入离散系数。离散系数是衡量样本数据中各数据值离散程度的一个统计量,计算式为
(14)

基于式(14),计算得出不同组合倾角溢流质量和出口速度的离散系数与平均值,如表3所示。
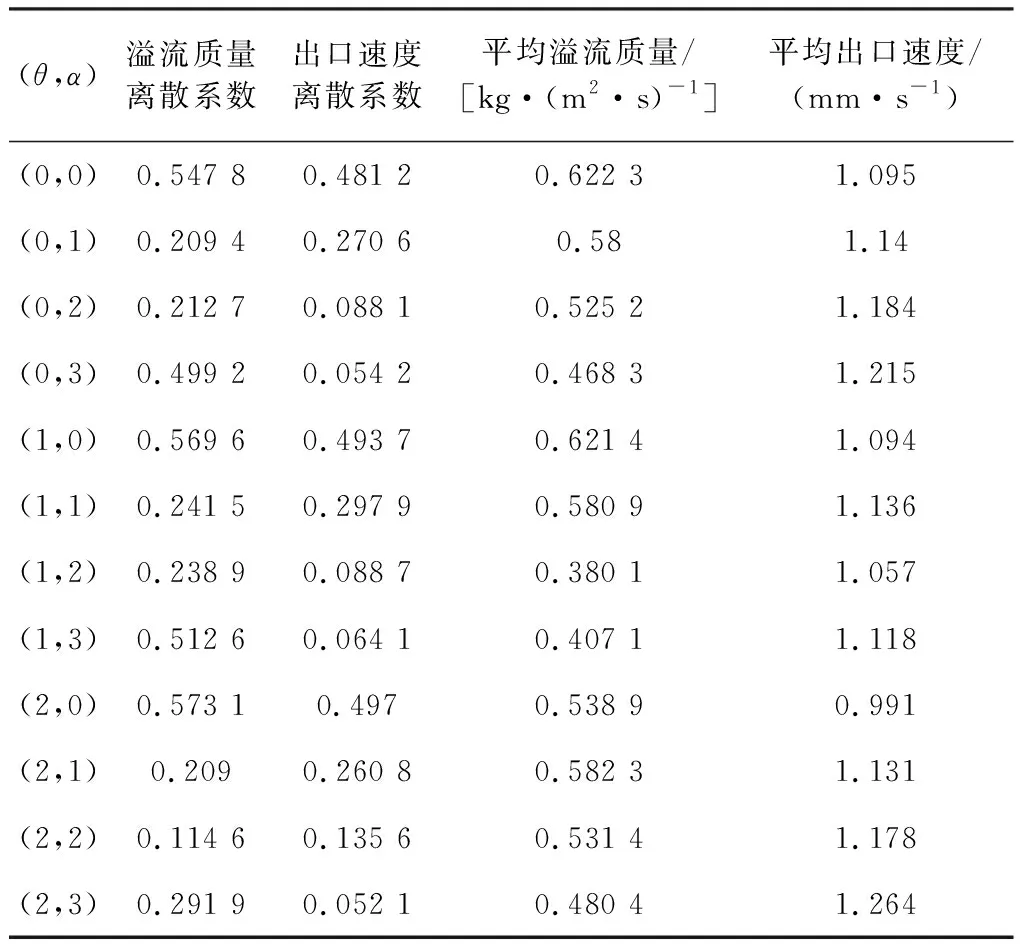
表3 溢流质量和出口速度的离散系数与平均值
从表3不难发现,在下倾角相同的情况下,不同角度的上倾角溢流质量离散系数大致呈现二次曲线的分布,而出口速度的离散系数大致呈现单调递减的分布。而在上倾角相同的情况下,不同角度的下倾角的溢流质量和出口速度的离散系数基本相差不大。由此可以确认上倾角角度比下倾角角度更能影响出口台阶上玻璃液的分布。根据表中不同组合倾角的平均溢流质量和出口速度可以看出,当上倾角为1°和2°时离散系数数值较小,且当上倾角为2°时,平均溢流质量波动较大,意味着实际的玻璃液分布情况会因为结构参数的误差而变得很大,需要更高精度的加工,不利于控制成本。
通过对比可知,当上倾角为1°,下倾角为2°时,玻璃液在溢流槽出口台阶上的分布较为均匀。最优解的相关仿真图如前文图4所示。
4 结束语
本文主要利用计算流体力学软件Fluent来设计了一种柔性玻璃新型成型工艺,并且模拟其合理性。通过对下拉法的成型过程进行数值模拟,分析了溢流槽的上、下倾角对溢流槽出口台阶上玻璃液分布情况的影响,对成型机构的设计以及工艺参数的控制提供了一定的参考依据。本文研究的主要结论如下:
1)对于溢流槽出口台阶上玻璃液的分布影响最大的是上倾角,不同角度的上倾角溢流质量离散系数大致呈现二次曲线的分布,而出口速度的离散系数大致呈现单调递减的分布;下倾角的角度变化则对溢流槽出口台阶上玻璃液的分布影响不大,并且出现远端玻璃液溢流量较小,近端玻璃液溢流量较大的现象。
2)当槽深为0.25 m,槽长为2 m,入口面积为0.025 6 m2,上下倾角分别为1°和2°,入口流速为0.004 m/s,玻璃液粘度为3 500 Pa·s 时,玻璃液在溢流槽出口台阶上的分布较为均匀。

