会“分”才会“解”

陈湘萍

数学课堂应该是智慧生长的课堂，在课堂上，学生不仅只是对知识本身的习得，更重要的是在探索的过程中所迸发的思维的火花。在问题解决的教学上更是如此，在问题解决之前，分析问题的过程尤为重要，这是解决问题的前提。我们先来看看影响学生分析问题的因素有哪些呢？

一、影响小学生分析问题能力的因素

第一，影响小学生分析问题能力的客观因素。一是问题情境本身。当问题情境的文字表达方式较为抽象，或者是不贴近小学生平时的生活经验时，会使小学生对问题难以理解，加大了分析问题的难度。或者，当问题情境太过生活化，呈现方式没有经过提炼，学生不懂如何去提取出相关的信息来分析问题。例如：A公园占地面积4000平方米，B公园占地面积5000平方米，C公园占地面积4000平方米。A公园有40个小朋友在玩，B公园有50个小朋友在玩，C公园有50个小朋友在玩。请问哪个公园更拥挤？学生明明已经具备解决这个问题所应有的知识和技巧，但是很多学生却感到无从下手。二是外界环境。由于小学生的年龄特点，外界干扰因素容易分散他们的注意力，使他们的思维受影响，不能专心分析问题。

第二，影响小学生分析问题能力的主观因素。一是惯性思维。根据心理学家的研究，人的生活经验会形成惯性思维，也称思维定势。当人面临熟悉的情境时，惯性思维会帮助人快速高效地解决问题;相反，当情境改变时，惯性思维则会阻碍人创造性地去解决新问题，造成思维刻板，影响思维的开放性;二是知识储备及生活经验。个体的知识储备和生活经验越丰富，那他分析问题时，就越多向性，越全面，那成功解决问题的可能性就越高。

二、如何在数学课堂中培养小学生分析问题的能力

1.多元表征，理解问题情境，有助于分析问题能力的提高

多元表征在新课教学中的价值不言而喻。在新知识教学中，学生通过多元表征及其之间的转化，有助于学生对新知识的内化和理解。而在问题解决时，多元表征有助于学生对问题情境的再分析和理解。

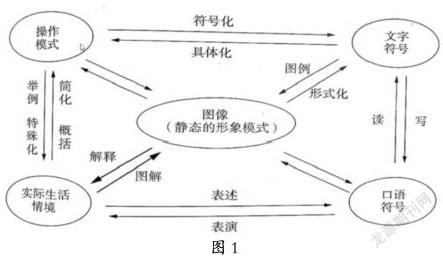
图1是莱什（Lesh）对布鲁纳动作、图形、符号三种表征的扩充。从下图中可以看出，莱什将符号表征细分为文字符号表征和口语符号表征，将动作表征分为操作模式表征和实际生活情境。

我们的问题解决总是来源于生活，再将它用文字符号表示出来，而学生需要理解这段文字符号，内化加工，才能選择合适的策略来解决问题。教学中大量例子表明，学生的问题就出现在理解题目中的文字符号上，即审题出现问题，导致解答错误。

根据皮亚杰的理论，学生思维层次的发展是从具体形象动作思维到抽象逻辑思维。教师可以通过多元表征，将题目中抽象的文字符号，转化成操作模式、实际生活情境、图像、口语符号。例如，“小聪家离学校有604米，他每天往返两趟，一共要走多少米？”很多学生列式：604×2=1208（米）。正确率只有10%，很多学生对题目中的“往返两趟”不理解。在讲解时，教师可以将这简洁的四个文字符号转化成实际生活情境和操作模式（教师在讲台上往返走了两趟，学生用手指头模拟小人从课桌一头走到课桌另一头，往返两趟），再引入口语符号（边“走”边说，让学生理解往返一趟是一来一回，往返两趟是两来两回，即四段）;最后再转化为图像（用笔在纸上画线段图，边画边讲）。通过这样的过程，将文字符号、实际情境、图像、口语符号、操作模式多元表征之间互相转化，让学生充分理解题目的意思，提升学生分析问题的能力，这样学生就不会再出错了。

2.从“开”到“收”，打破惯性思维，有助于分析问题能力的提高

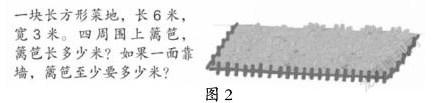
在问题解决教学中，教师可以巧妙利用课本的练习进行微小变式，分解问题，增加问题的开放性，打破思维惯性，发展思维的灵活性和发散性。例如，下图2。

第一步，入。教师先把配图处理一下，只出现一块长方形菜地，然后配字“一块长方形菜地，长6米，宽3米。四周围上篱笆，篱笆长多少米？”这个问题是求长方形周长，学生很快列出：（6+3）×2=18（米） 6×2+3×2=18（米）。

第二步，开。教师继续出示“如果一面靠墙，篱笆要多少米？”（长方形菜地上不出现篱笆），引导学生画图思考，学生可能出现以下两种画图的情况：即长靠墙或宽靠墙，通过小组合作交流讨论，所有学生都明确有两种情况。然后，分别计算，长靠墙的情况：可能出现18-6=12（米）、或者6+3×2=12（米） 、6+3+3=12（米）这三种计算方法。这其实是两种不同的分析方法，一种是在4面都围篱笆的基础上减去一条长，一种是直接计算不靠墙的3条边的和。同理，宽靠墙的情况：可能出现18-3=15（米），或者6×2+3=15（米）、6+6+3=15（米）。

第三步，收。教师在“篱笆要多少米？”中间加入“至少”，即变为“篱笆至少要多少米？”此时，水到渠成，学生自然而然地明白至少要12米，即选择长靠墙的情况。

以上例子中，教师将课本练习做了微小的调整，分解了问题，使得题目更具开放性，通过数形结合，得出两种情况，再回归到问题本身“至少”。在整个过程中，学生思维的灵活性和发散性得以发展，培养了学生思维的缜密性，提高了学生分析问题的能力。

3.小组合作交流，扩大知识储备和生活经验，有助于分析问题能力的提高

三人行必有我师。每个学生的生活背景不同，生活经验不同，看待问题的角度也不同。因此当学生们在和同伴分组交流讨论时，可以取长补短，使得分析问题时更全面。而且在互帮互助的氛围中，学生更容易投入思考和学习中，教师可以多采用小组合作的方式，让学生在同伴的陪同下，拓展知识面和生活经验，可以拓宽学生分析问题的思路和方向，提升分析问题的能力。

4.非常规作业，注重学生的感受和生活经验的积累，有助于分析问题能力的提高

日常的作业除了一些常规的模仿训练之外，教师还应多布置一些感受类实践类的非常规作业。例如，认识了长方体、正方体之后，我一般都会布置学生做一个长方体框架和一个正方体框架。在完成这个实践性作业的过程中，学生对于长方体和正方体的特征认识更深刻，在日后遇到这方面的问题解决时，分析起来都是头头是道。

在日常教学中，教师要通过多元表征帮助学生理解问题情境，精心设计教学从“开”到“收”，发展思维的灵活性和发散性，利用小组合作交流和非常规作业有意识地着重去培养学生分析问题的能力，提升学生的逻辑思维能力和综合素质。