轮毂电机电动汽车扭力梁悬架匹配设计及平顺性优化分析

高兆桥，杨 坤，2，王 杰，李守好，陈 玉，刘庆新

(1.山东理工大学 交通与车辆工程学院，山东 淄博 255000；2.山东意威汽车科技有限公司，山东 淄博 255000；3.北汽福田汽车股份有限公司诸城汽车厂，山东 诸城 262200)

轮毂电机电动汽车由于结构紧凑、传动效率高、能够实现四轮转矩独立控制，成为电动汽车的重要发展方向之一[1-3]。轮毂电机电动汽车使用轮毂电机直接驱动汽车，可简化传动系统，提高传动效率，改善整车经济性，而电动汽车采用轮毂电机的方案后，会占用悬架的安装空间[4-5]。扭力梁悬架因具有结构简单、成本低的优点，成为经济型轮毂电机电动汽车后悬架的主流[6]。同时考虑到轮毂电机集成在车轮内会使汽车非簧载质量增加，从而导致轮胎接地性能和整车平顺性变差[7-9]。因此针对适用于轮毂电机电动汽车的扭力梁悬架开展优化设计研究具有较强的理论意义。

针对这一问题，国内外学者从不同的方面开展了研究。Mitra等[10]使用遗传算法优化悬架的刚度和阻尼，减小了车身加速度，但是其路面输入为半正弦输入，不能反映路面真实的情况。Wei等[11]对比集中式电机驱动和轮毂电机驱动的方案，考虑轮毂电机振动的影响，对电机悬置机构进行参数优化，消除了由轮毂电机振动造成的共振峰值。李小彭等[12]通过遗传算法优化悬架的刚度和阻尼，对衬套优化选型，提升了悬架的减振性能。郭浩敏等[13]在轮毂电机电动汽车的悬架上加装动力吸振器，对不同质量的动力吸振器进行仿真对比，减小了高频处车身加速度和相对动载，改善了整车平顺性和行驶安全性，但是动力吸振器的引入使整车质量增加，影响整车经济性，且在低频处动力吸振器的减振效果不明显。郑阳等[14]提出一种改进遗传算法，以车身垂向加权加速度均方根值和俯仰角均方根值为优化目标对悬架参数进行优化，改善了整车平顺性，但未考虑悬架动挠度和轮胎动载荷的变化对平顺性的影响。陈齐平等[15]以车轮振动最大位移的最小值为目标函数对悬架优化设计，改善了悬架的平顺性，但未考虑车身加速度和轮胎动载荷对平顺性的影响。

本文基于轮毂电机电动汽车的特点，完成了轮毂电机的参数匹配、扭力梁悬架的匹配设计和校核。基于Matlab/Simulink搭建1/4车辆动力学模型，并以车身加速度、悬架动挠度和相对动载3个指标均方根和的最小值为优化目标，对轮毂电机电动汽车悬架弹簧刚度和减振器阻尼系数进行优化设计并通过优化前后车身加速度及车身加速度功率谱密度进行验证。

1 轮毂电机及扭力梁悬架匹配设计

1.1 轮毂电机的参数匹配

轮毂电机电动汽车整车参数如表1所示。

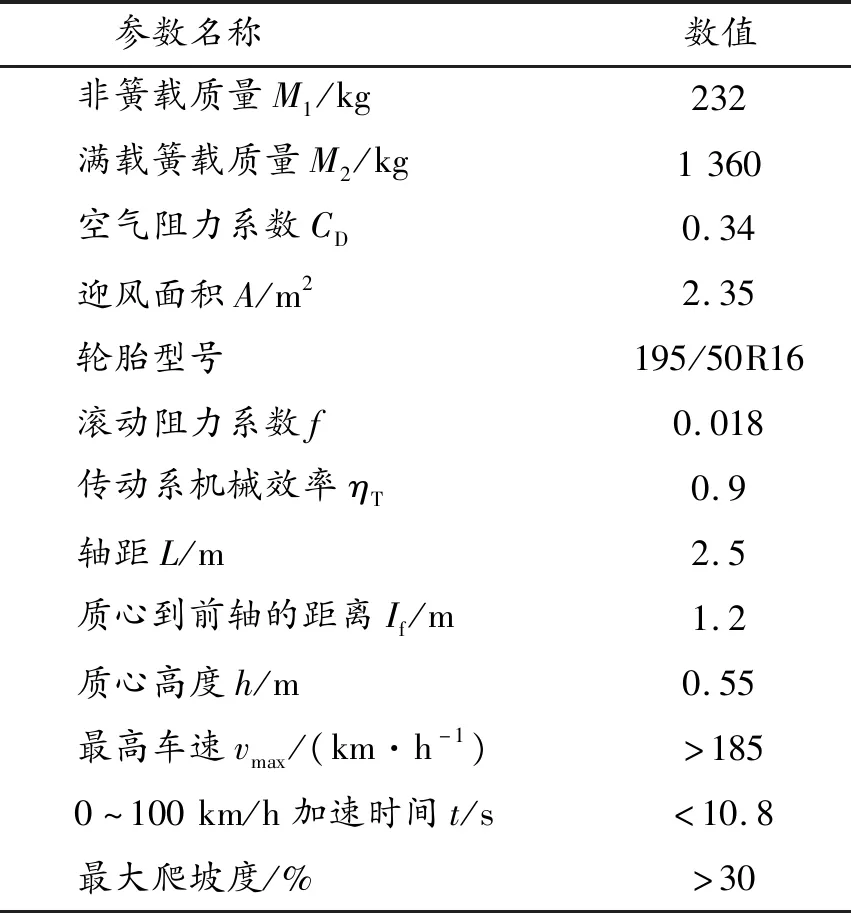
表1 整车参数

轮毂电机电动汽车采用四轮驱动方案，每个电机的质量为25 kg。基于整车参数，由整车动力性指标确定电机性能参数。其中，电机峰值功率应满足轮毂电机电动汽车对最高车速、最大爬坡度和加速时间的要求，电机峰值转矩应满足轮毂电机电动汽车对最大爬坡度和最大加速度的要求，电机的最高转速应满足轮毂电机电动汽车最高车速的要求[16]。

匹配后的电机性能参数如表2所示。

表2 电机性能参数

1.2 悬架参数的确定

悬架的主要参数有偏频、静挠度、动挠度、弹簧刚度和减振器阻尼系数。

1)偏频

对于传统乘用车，后悬架满载偏频要求在1.17～1.58 Hz内，采用轮毂电机方案后，簧下质量增大，平顺性变差，应选择较小的偏频以保证整车平顺性，因此偏频选为1.2 Hz。

2)悬架的静挠度

选定偏频以后，由式(1)可计算出悬架的静挠度。

(1)

式中：fc为悬架的静挠度；n为悬架的偏频。

3)悬架的动挠度

传统乘用车动挠度要求在7～9 cm内，采用轮毂电机方案后，簧下质量增大，使车身与车轮在垂向的相对位移增大，因此动挠度选为9 cm。

4)弹簧刚度

k=m2(2πn)2

(2)

式中：k为悬架弹簧的刚度；m2为满载簧载质量。

5)减振器阻尼系数

(3)

式中：c为减振器阻尼系数；ψ为相对阻尼系数；θ为减振器轴线与铅垂线之间的夹角，取θ=5°。

匹配后的悬架参数如表3所示。

表3 悬架参数

2 悬架强度校核

2.1 悬架建模

使用三维建模软件CATIA建立扭力梁后悬架的模型，并导入ANSYS Workbench中，划分网格后如图1所示。

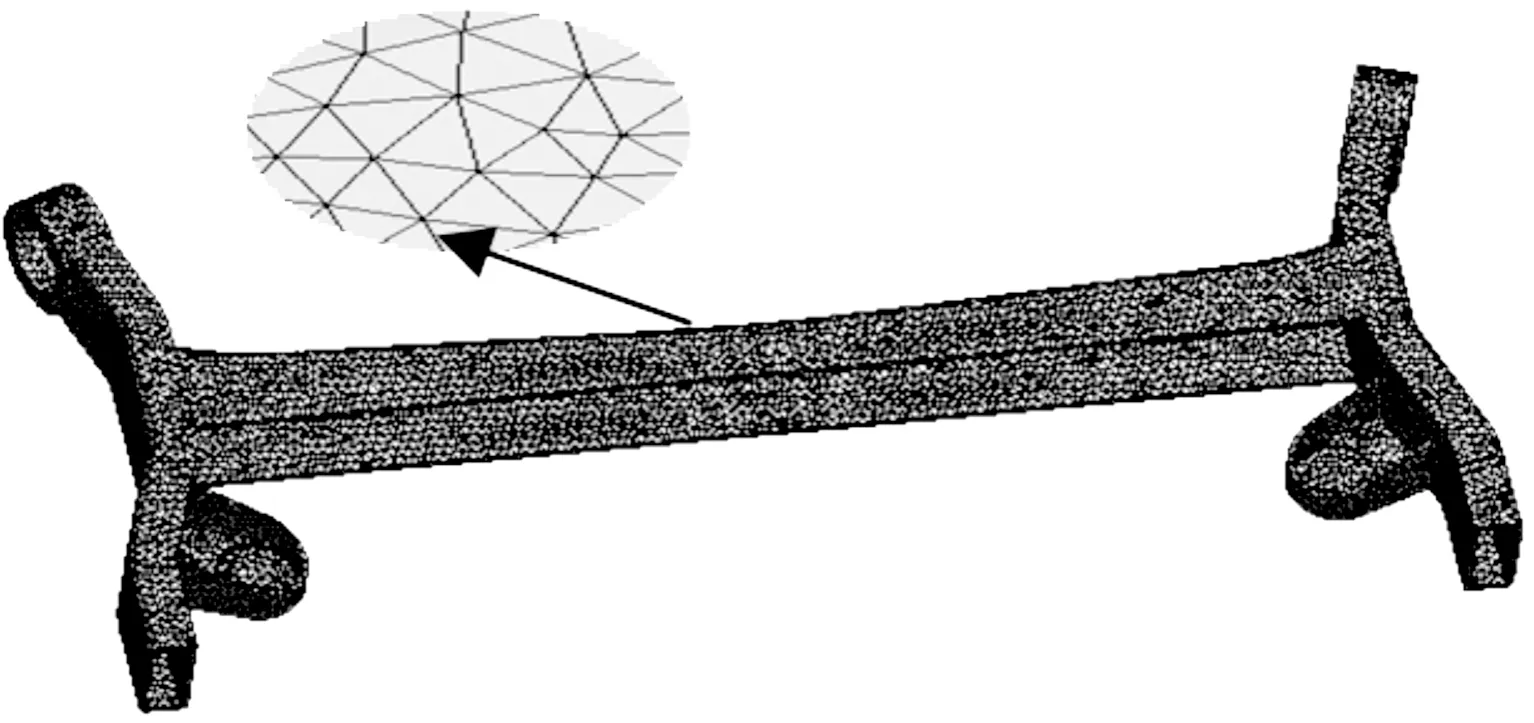
图1 扭力梁悬架网格模型

2.2 校核工况分析

为了校核扭力梁悬架的强度，选取倒车紧急制动工况、极限转向工况和双侧过凸包工况3种后悬架受力较大的工况进行强度分析[17]。

2.2.1倒车紧急制动工况

汽车倒车紧急制动时，载荷后移，在车辆坐标系下，整车加速度沿x轴正方向，大小为0.6g，相应的载荷如下：

(4)

(5)

式中：Fz1为地面对左后轮的垂向力；Fz2为地面对右后轮的垂向力；m为整车质量；L为轴距；If为质心到前轴的距离；a为整车制动减速度；h为质心高度；g为重力加速度；Fx1为左后轮的纵向制动力；Fx2为右后轮的纵向制动力。

2.2.2极限转向工况

汽车极限右转时，载荷左移，在车辆坐标系下，整车加速度沿y轴负方向，大小为0.7g，相应的载荷如下：

(6)

(7)

(8)

(9)

式中：Fy1为左后轮侧向力；Fy2为右后轮侧向力；Fz1为地面对左后轮的垂向力；Fz2为地面对右后轮的垂向力；ay为整车侧向加速度。

2.2.3双侧过凸包工况

汽车双侧过凸包时，在车辆坐标系下，整车加速度沿z轴正方向，大小为2g，纵向力的增量约为垂向力增量的2/3[17]。相应的载荷如下：

(10)

(11)

式中：Fz1为地面对左后轮的垂向力；Fz2地面对右后轮的垂向力；az为整车垂向加速度；Fx1为地面对左后轮的纵向力；Fx2为地面对右后轮的纵向力。

2.3 强度校核

扭力梁悬架采用的材料是Q345钢，其屈服强度为345 MPa，扭力梁在各工况下所受应力需小于许用应力。

(12)

式中：[σp]为许用应力；σp为屈服强度；n为安全系数，取n=1.2。

基于整车参数及式(4)～(11)，计算得到各个工况载荷，如表4所示。

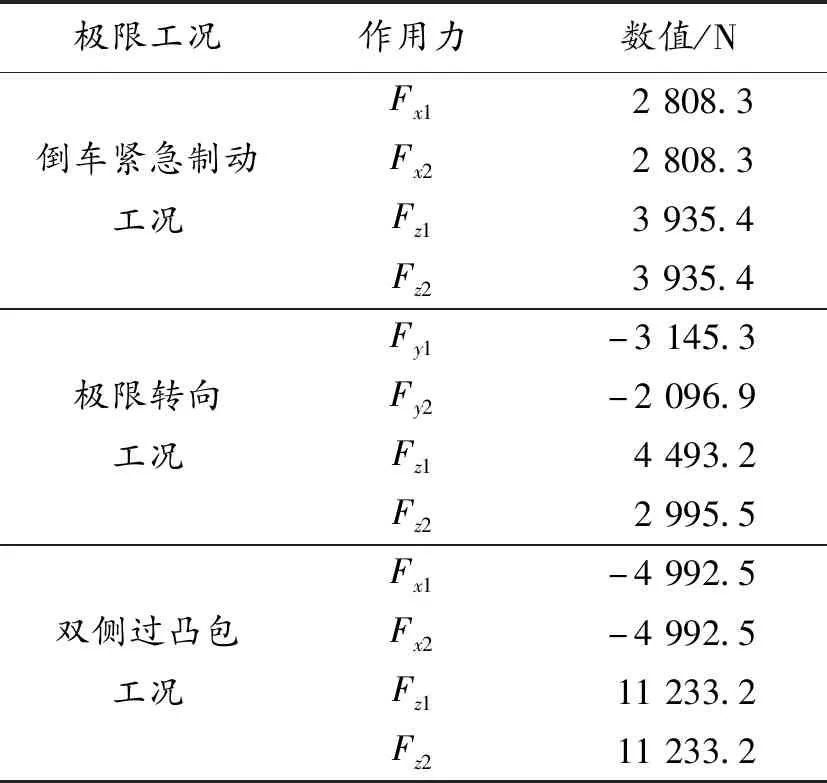
表4 各工况后轮受力

对倒车紧急制动工况，取动载系数为1.5，极限转向工况和双侧过凸包工况的动载系数均取1[18]。在ANSYS Workbench中，对扭力梁悬架施加相应工况下的载荷和约束，可计算出3种极限工况下的应力云图，分别如图2～4所示。由应力云图可知，倒车紧急制动工况最大应力为182.42 MPa，极限转向工况最大应力为148.36 MPa，双侧过凸包工况最大应力为283.45 MPa，3种工况的最大应力均未超过许用应力287.5 MPa，强度满足要求。

图2 倒车紧急制动工况应力云图

图3 极限转向工况应力云图

图4 双侧过凸包工况应力云图

3 疲劳寿命分析

3.1 1/4车辆动力学模型

目前乘用车的簧载质量分配系数接近1，前后悬架的垂直运动可认为相互独立，所以汽车振动系统可以简化为2个自由度的振动系统，1/4车辆动力学模型的主要参数如表5所示。

表5 1/4车辆动力学模型主要参数

(13)

式中：m2为簧载质量；m1为非簧载质量；k为悬架刚度；c为减振器阻尼系数；z1为车轮垂向位移；z2为车身垂向位移；kt为轮胎刚度；q为路面不平度函数。

3.2 疲劳寿命计算

在Matlab/Simulink中建立1/4车辆动力学模型，仿真并输出悬架与车轮相连处所受垂向力随时间的变化曲线，将该曲线作为悬架承受的交变载荷导入到ANSYS Workbench中进行悬架的疲劳寿命分析，结果如图5所示，据此可以得到扭力梁悬架的最小循环次数。其中，受力曲线对应的各个等级路面的比例如表6所示，各个等级路面车速的比例如表7所示[19]。

图5 扭力梁疲劳寿命云图

表6 各等级路面占比

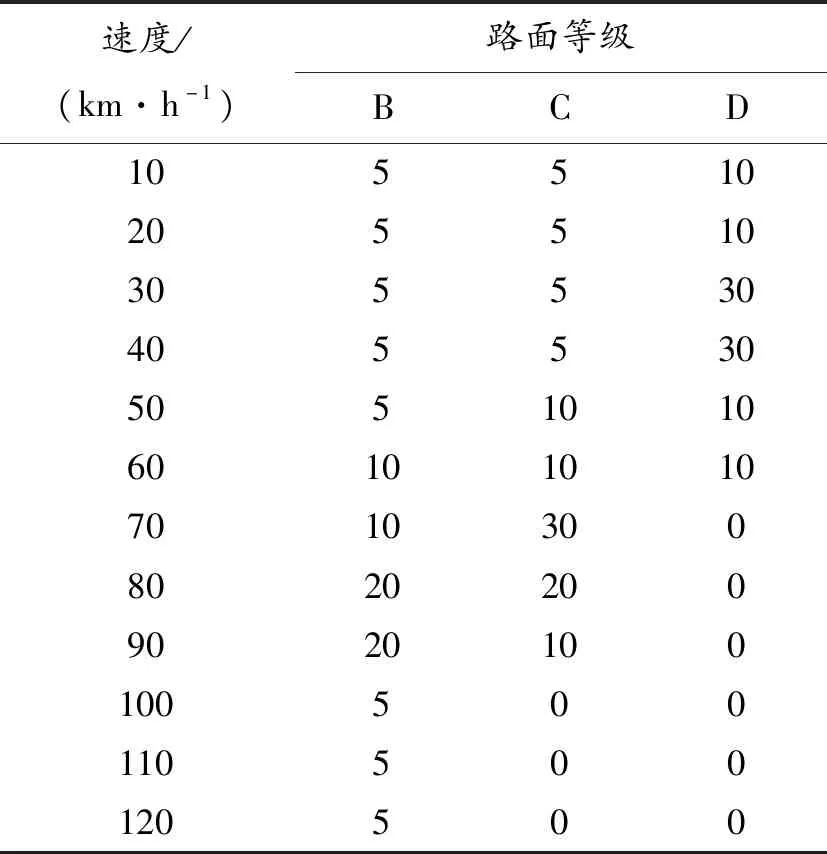
表7 各等级路面车速占比 %

由图5可知，扭力梁的最小疲劳寿命为110 170次循环，每个循环续驶里程为5 726 m，此扭力梁的疲劳寿命为630 800 km。

4 基于粒子群算法的扭力梁悬架参数优化及验证

4.1 粒子群算法

粒子群算法从随机解出发，通过迭代寻找最优解，它通过适应度来评价解的品质，具有高效的搜索能力，可快速计算出多目标意义下的最优解。同时，粒子群算法的通用性较好，适合处理多种类型的目标函数和约束，其流程如图6所示。

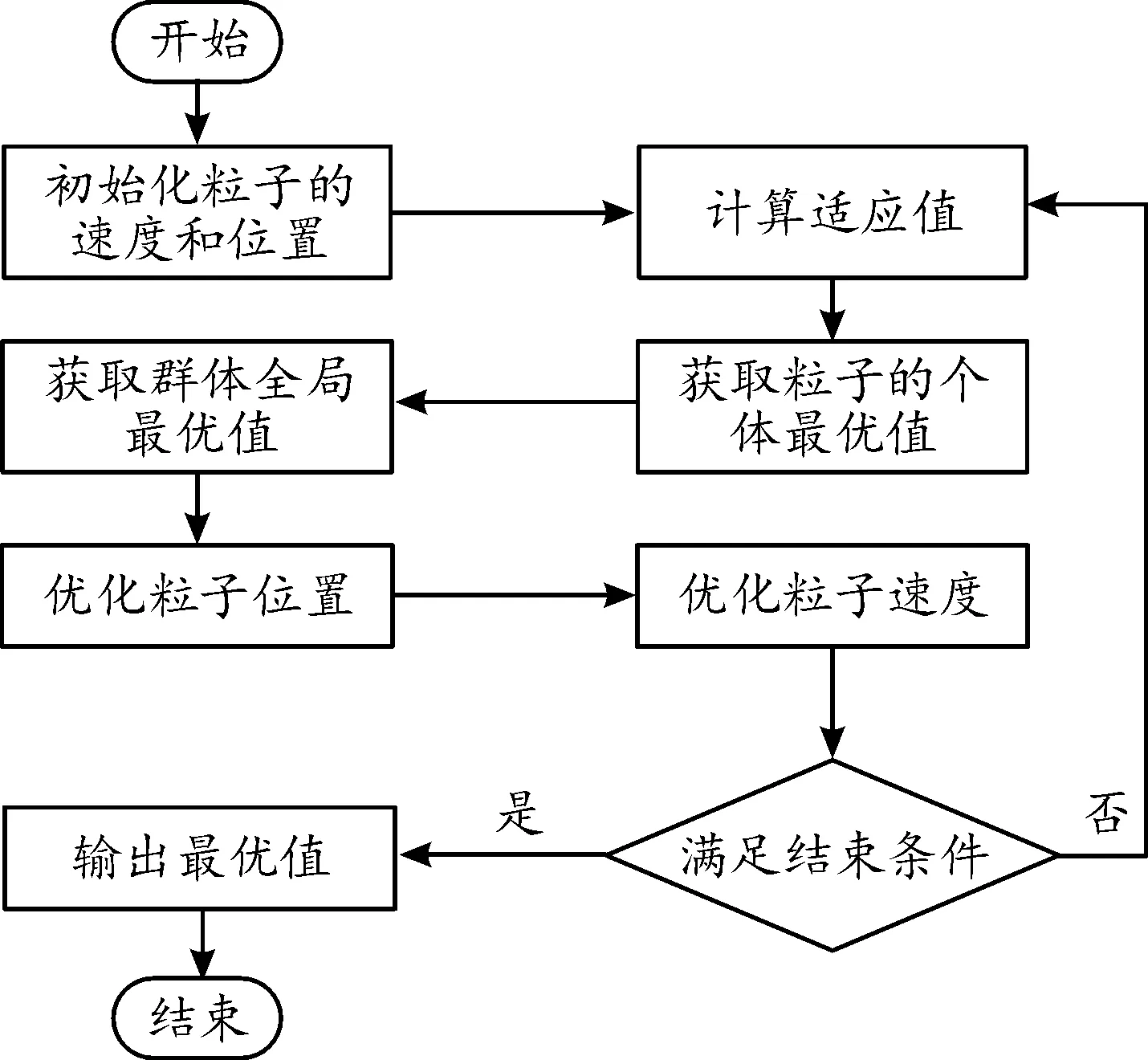
图6 粒子群算法流程框图

4.2 基于粒子群算法的悬架参数优化

非簧载质量增加使车身垂向振动效应增加，整车平顺性变差，为了减小这种影响，需要对扭力梁悬架参数进行优化设计。基于在Matlab/Simulink中搭建的1/4车辆动力学模型，选取粒子群优化算法，设定约束条件，可算出悬架弹簧最优刚度和减振器最优阻尼系数。

大量的测量表明：路面随机输入和汽车的振动响应基本上符合正态分布[20]。乘用车的限位行程选取为9 cm，现要求撞击悬架限位的概率为0.3%，悬架动挠度为σfd，根据正态分布的规律可知，[fd]=3σfd，此时悬架动挠度的标准差为3 cm。

车轮与地面间动载Fd的方向是上下交变的，当Fd与车轮作用于路面的静载G方向相反且大小相等时，车轮作用于路面的垂直载荷为零，这会严重影响整车的行驶安全性。通常取G=3σFd，此时相对动载的标准差σFd/G=1/3。由正态分布的规律可知，此时车轮跳离地面的概率为0.15%[20]。

综合考虑车身加速度、悬架动挠度和车轮相对动载对平顺性的影响，以3个指标均方根加权和的最小值为优化目标，适应度函数为：

(14)

相应的约束条件为：

(15)

粒子群算法适应度函数如图7所示。

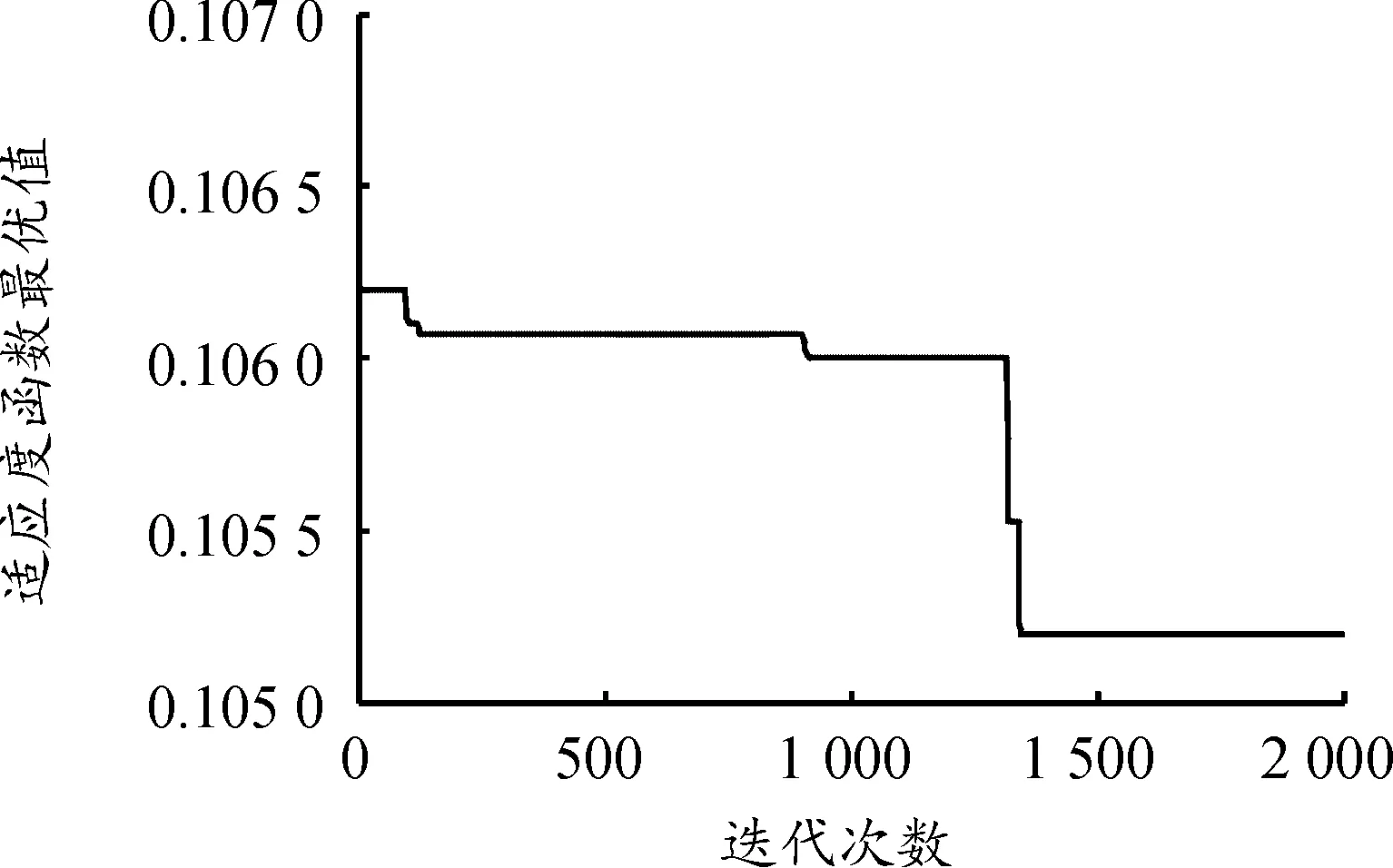
图7 适应度函数

粒子群算法在1 352次迭代之后，适应度函数达到最小值，经粒子群优化后的结果为，k=14 271 N/m，c=1 216 N·s·m-1。

4.3 平顺性分析及验证

为了验证经粒子群优化后整车的平顺性是否得到改善，以C级路面为例，在车速为72 km/h的条件下，使用Matlab仿真出优化前后车身加速度随时间变化的曲线，如图8所示。

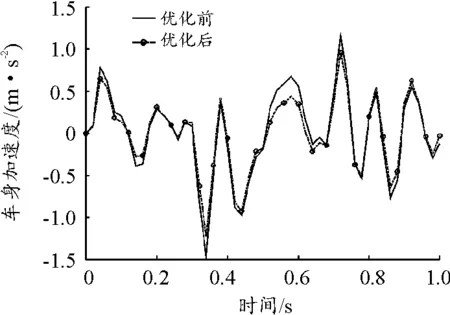
图8 车身加速度曲线

粒子群优化前后整车平顺性评价指标如表8所示。优化后悬架动挠度和相对动载在约束条件范围内，车身加速度均方根值减小了0.078 5 m/s2，与优化前相比减小了14.5%。

表8 平顺性评价指标

随机输入下，优化前后车身加速度功率谱密度、悬架动挠度功率谱密度和相对动载功率谱密度分别如图9～11所示。

图9 车身加速度功率谱密度曲线

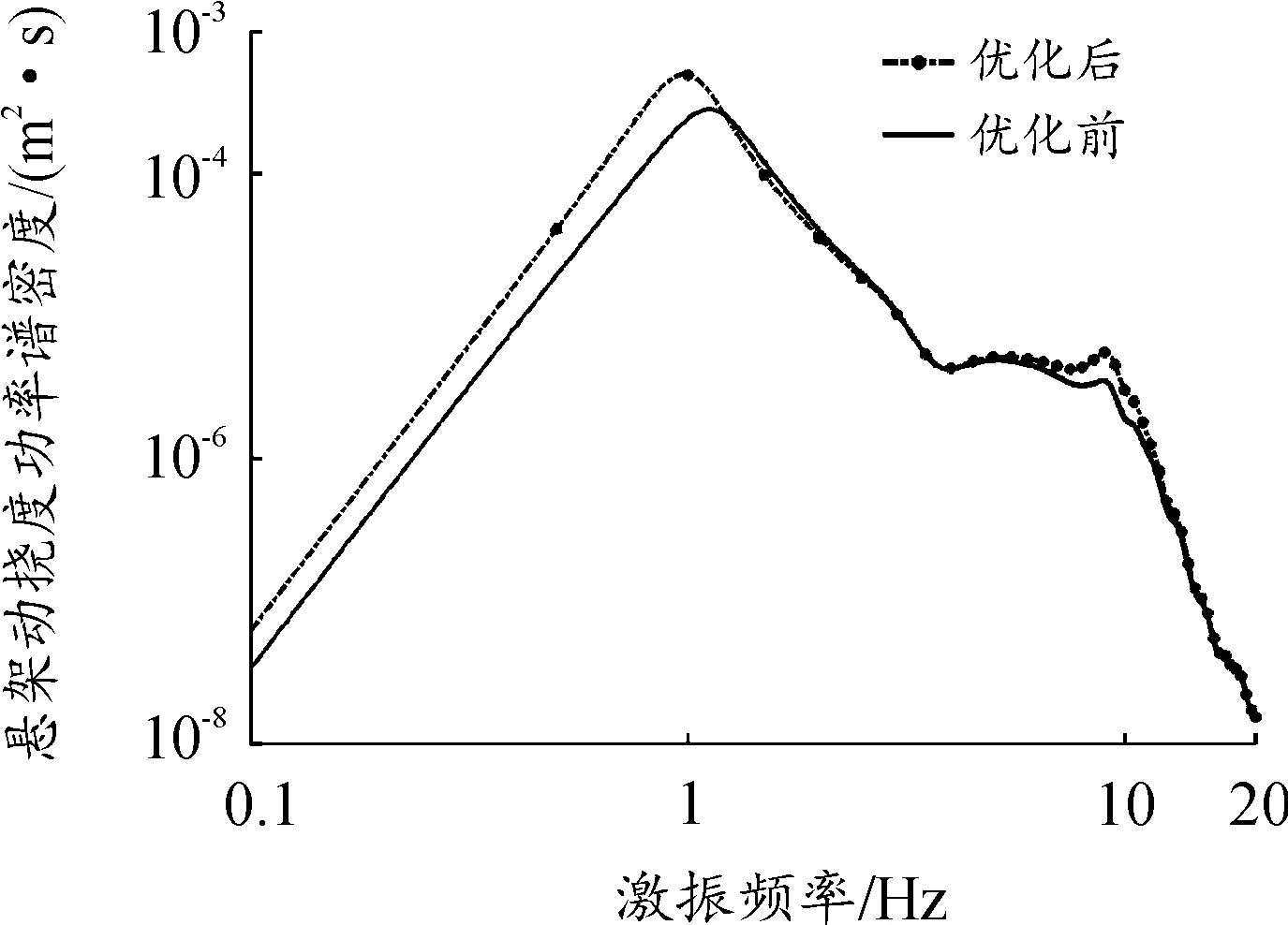
图10 悬架动挠度功率谱密度曲线

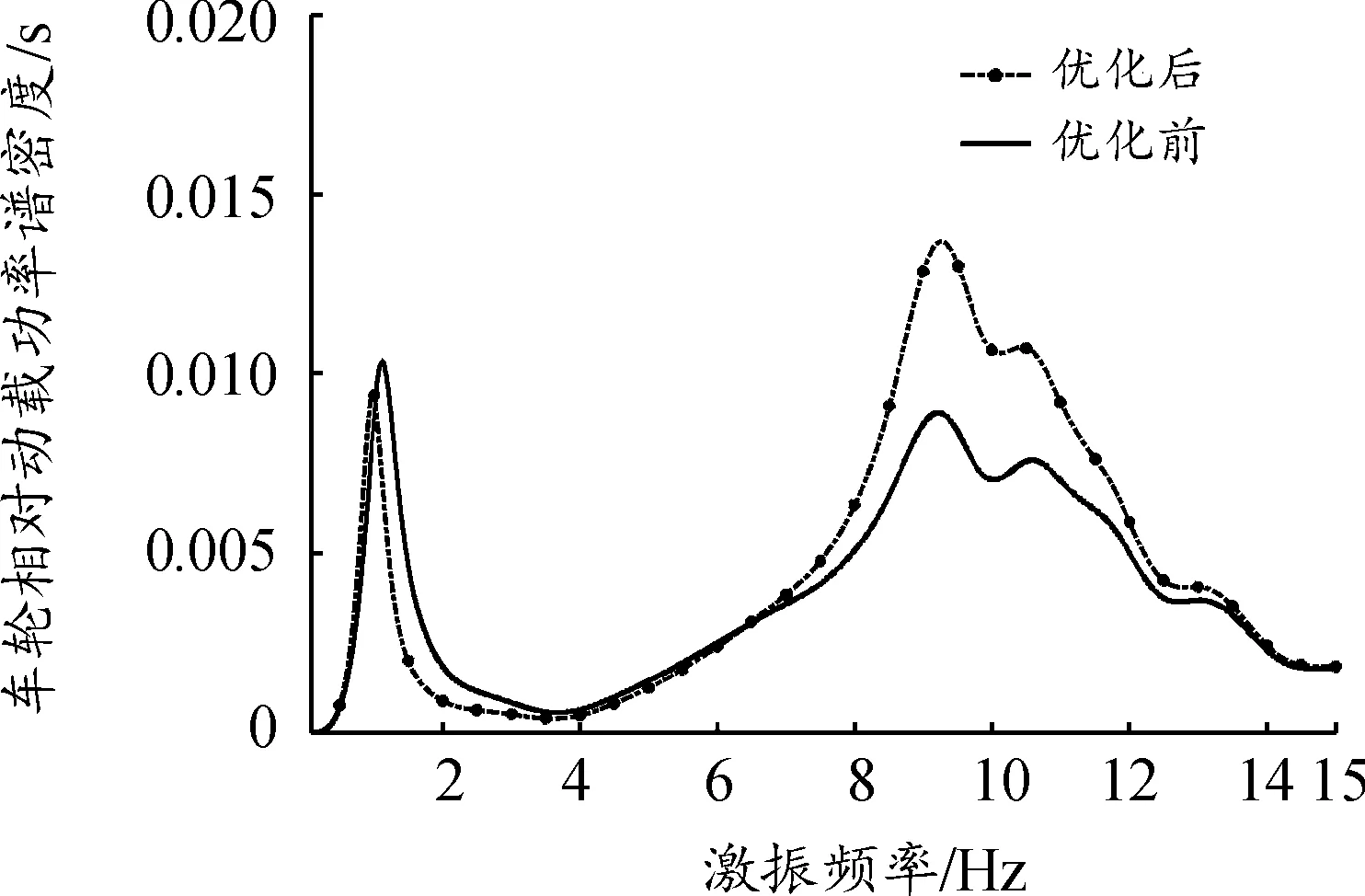
图11 车轮相对动载功率谱密度曲线

优化前后随机响应的低频共振幅值如表9所示。

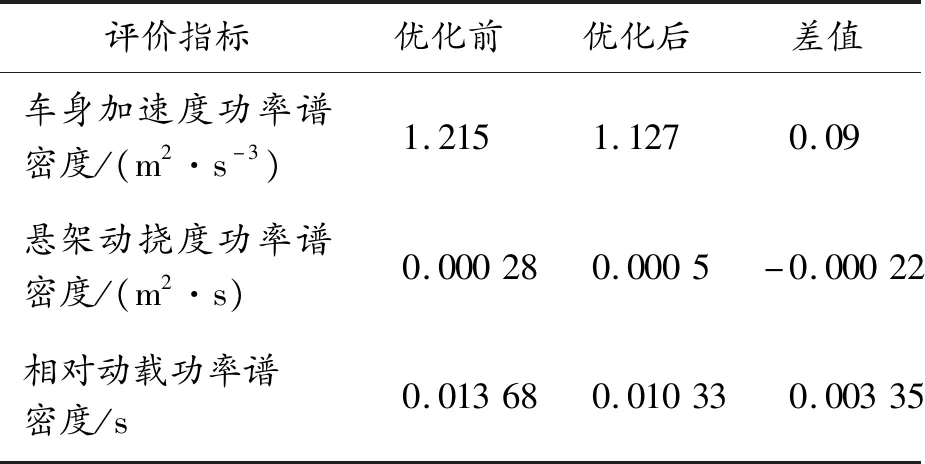
表9 随机响应的低频共振幅值

车身加速度功率谱密度和相对动载功率谱密度的低频共振幅值分别减小了0.09 m2/s3和0.003 35 s，与优化前相比分别减小了7.4%和24.5%；悬架动挠度功率谱密度增加了0.000 22 m2·s，扭力梁悬架与优化前相比有更好的低频减振性能。

5 结论

1)悬架参数经粒子群优化后，弹簧刚度由19 329 N/m减小至14 271 N/m，减振器阻尼系数由1 550 N·s·m-1减小至1 216 N·s·m-1。结果表明：同时减小弹簧刚度和减振器阻尼系数可减小车身加速度，提升悬架减振性能，改善汽车平顺性。

2)针对1/4车辆动力学模型进行时域和频域仿真分析，车身加速度均方根值减小14.5%，车身加速度功率谱密度的低频共振幅值减小7.4%，整车平顺性改善，相对动载功率谱密度的低频共振幅值减小24.5%，整车行驶安全性提高。