考虑磁场影响的磁性形状记忆合金分段线性化超弹性本构模型研究

陈 超，陈 鑫，刘 涛，孙 勇，还 毅，唐柏鉴

(1. 苏州科技大学江苏省结构工程重点实验室，苏州 215011；2. 江苏省住房和城乡建设厅，南京 210036；3. 江苏省建筑科学研究院有限公司，南京 210008；4. 中央军委后勤保障部工程质量监督中心，北京 100373)

自20 世纪60 年代被发现以来，传统形状记忆合金(Shape Memory Alloy, SMA)的温控形状记忆效应和超弹性效应受到广泛关注，其应用于医疗、土木[1−5]、机械工程等领域的研究已较为成熟。随着对SMA 研究的不断深入，传统形状记忆合金在实际应用中的局限性开始显现。为此，研究人员推测这种形状记忆效应可以通过对马氏体状态下的铁磁合金施加磁场得到，并着手开始研发。1996 年，Ullakko 等[6]首次在Ni2MnGa 单晶中获得0.2%的磁致可恢复应变，磁性形状记忆合金(Magnetic Shape Memory Alloy，MSMA)的研究开始受到关注。

MSMA 不仅与SMA 一样，其变形可以受温度和应力控制，还可以受磁场控制，且具有较大的输出应变。传统SMA 变形机制主要有马氏体相变和马氏体重定向两种，而MSMA 变形机制则更为复杂，除马氏体相变和马氏体重定向外，还存在磁畴旋转以及畴壁运动两种与磁性相关的变形机制。根据MSMA 变形诱发条件不同，MSMA 的磁-力耦合变形机制可以总结为以下四类[7]：1)磁场诱发马氏体重定向；2)应力诱发马氏体重定向；3)磁场诱发马氏体相变；4)应力诱发马氏体相变。

材料本构模型既是MSMA 热-磁-力学内在变形机制的重要表征，也是MSMA 走向工程应用的重要基础。为此，国内外学者基于不同的理论、从不同的角度提出了一系列MSMA 磁-力耦合本构模型。陈鑫等[8]对已建立的MSMA 本构模型进行了综述，指出统一的、面向工程应用的简化模型有待进一步研究。冯元慧[9]基于热力学原理，建立了磁性形状记忆合金的热-磁-力耦合本构模型。Chen 等[10]考虑温度效应，建立了可以描述MSMA在三维加载工况下马氏体重定向行为的力学模型。LaMaster 等[11]提出了基于热力学原理的MSMA 连续介质模型，精准描述了MSMA 在任意三维加载下的力学行为。Auricchio 等[12]从晶体学基本原理出发，考虑三个马氏体变体，建立了三维单晶唯象本构模型，对MSMA 在复杂加载条件下的马氏体相变和重定向过程给出了合理的描述及预测。龚臣成等[13]基于热力学及能量耗散概念，推导了一种MSMA 的磁-力耦合三维唯象本构关系，通过内变量的形式模拟微观相结构及磁结构的演化，该模型考虑了马氏体重定向过程及马氏体逆重定向过程。胡升谋[14]基于实验数据，结合能量守恒定律与热力学理论，利用参数辨识方法，预测了多场耦合变量曲线，构建了MSMA 多场耦合模型。Mousavi 和Arghavani[15]建立了一个能更全面描述MSMA 变形行为的三维宏观唯象本构模型，该模型考虑了三种与磁致应变相关的变形机制，即马氏体重定向、畴壁运动和磁畴旋转，对MSMA变形机制进行了较为全面的描述。Rogovoy 等[16]建立了一个模型用于描述磁场控制MSMA 变形过程，并利用已有的实验数据对模型进行了验证。Jafarzadeh 等[17]对MSMA 进行相关实验，研究了加载历史对MSMA 重定向的影响，并在此基础上建立了一个关于MSMA 的唯象模型。Bartel 等[18]依赖于能量松弛的概念提出了一种MSMA 本构模型框架，用以预测微观结构演化。Chen 等[19]进一步改进了其于2014 年提出的相变本构模型，并将其应用于质量-弹簧结构中，分析了Zhang 等[20]发现的高频磁场作用下的MSMA 力学行为。Yu 等[21]通过引入内部状态变量，在热力学框架下建立了多晶MSMA 的热-磁-机械耦合模型，该模型论述了磁化过程中发生的退磁效应，并通过相应实验，对模型进行验证。Shi 等[22]分析了MSMA 磁诱导应变的原理及相应的本构方程，并搭建试验平台证明了MSMA 在执行器应用中的优越性。Bartel等[23]基于能量理论建立了MSMA 建模框架，检验了简单加载情况下的二维模型，并对较为复杂的加载情况(非比例双轴应力、正交磁场)进行响应预测。

目前，针对MSMA 建立的本构模型大多基于热动力学、细观力学等理论，通过严密的力学推导获得，此类模型在理论研究和材料性能精确描述方面存在一定的优势，但往往表达形式复杂、物理参数多、参数标定难、计算效率低等问题，给MSMA 的工程应用带来了一定的困难。因此，如何确定关键参数，进而在满足工程精度的基础上简化复杂的理论模型，使其满足形式简单、参数少、效率高等工程应用需求，是MSMA 走向工程应用的关键之一。

因此，本文将围绕MSMA 在环境温度处于马氏体相变完成温度Mf以下时，应力诱发马氏体重定向的力学行为描述进行研究。Karaca 等[24]、Chen 等[10]和Feigenbaum 等[25]均已对该变形机制进行了理论阐述，本文将在上述研究的基础上，统计分析Couch 等[26]、刘小双[27]、Straka 等[28]、Sarawate等[29]的材料试验数据，基于经典塑性理论框架，建立考虑磁场影响的MSMA 分段线性化超弹性本构模型，以期准确预测MSMA 在不同环境磁场下的应力-应变曲线。首先，根据MSMA 超弹性特性，建立其一维分段线性化本构模型；随后，利用塑性理论框架，扩展建立MSMA 多维分段线性化本构模型；再根据试验数据建立基于Logistic 函数的临界应力-磁场关系函数；最后，从滞回曲线和滞回耗能两个方面对比理论模型与试验结果的误差。

1 超弹性MSMA 应力-应变关系描述

1.1 完全加卸载下MSMA 应力-应变关系

研究相关文献中已有的MSMA 力学性能试验结果[30]，结合已有本构模型，考虑对MSMA 受磁场影响的超弹性特性预测的工程应用要求，作如下基本假定：

1)在外部环境磁场强度和温度一定的情况下，根据MSMA 在应力作用下的受力特点，完全加载下其各状态(完全单一应力择优取向马氏体变体状态、应力择优取向马氏体变体、磁场择优取向马氏体变体相互过渡状态以及完全单一磁场择优取向马氏体变体状态)一维应力-应变关系曲线简化为四折线形式(图1)；

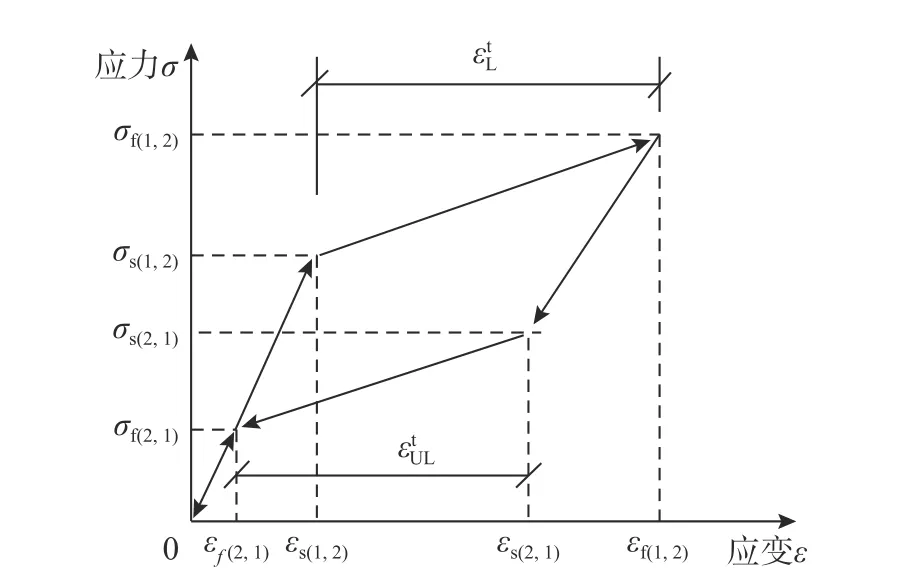
图1 完全加载下MSMA 分段线性化应力-应变关系Fig. 1 Segment linearized stress-strain relationship of MSMA under fully loading

2) MSMA 始终在最大可恢复应变范围内工作，同时环境磁场H始终处在马氏体逆重定向完成磁场以上；

3) MSMA 塑性不可压缩，忽略重定向及逆重定向过程引起的体积变化；

4) MSMA 发生马氏体重定向和逆重定向的临界应力与外部环境磁场有关；

5)不考虑MSMA 在外加磁场作用下出现的退磁效应。

σs(1,2)σf(1,2)σs(2,1)σf(2,1)

图1 中：、、、分别为马氏体重定向开始应变和结束应力、马氏体逆重定向开始应力和结束应力。由图可得临界应力和临界应变的关系如下：

1.2 加载不完全即卸载及卸载不完全即加载情况下MSMA 应力-应变关系

在加载不完全即卸载及卸载不完全即加载情况下，由相关试验结果及MSMA 本构模型理论曲线可知：MSMA 重定向及逆重定向过程应力-应变曲线接近于直线，为简化分析，将重定向及逆重定向曲线段简化为直线段，起始点为重定向开始点，终点为重定向完成点；同样，将逆重定向曲线段简化为直线段，起始点为逆重定向开始点，终点为逆重定向完成点。建立MSMA 超弹性分段线性化模型如图2 所示。

图2 加载不完全即卸载及卸载不完全即加载情况下MSMA 分段线性化应力-应变关系Fig. 2 MSMA segment linearized stress-strain relationships for incomplete unloading and incomplete loading

2 MSMA 分段线性化超弹性本构模型

2.1 马氏体重定向方程

2.2 马氏体重定向和逆重定向起始面微分方程

在MSMA 在重定向及逆重定向过程中，类比马氏体重定向诱发的应变为塑性应变，则弹性应变张量增量和塑性应变增量之和为Green-Lagrange应变张量，即：

式中：Λmn为重定向张量，在马氏体重定向及逆重定向过程中值不同；dξσ为应力择优取向马氏体变体的体积百分数增量，则由式(5)、式(6)、式(7)可得：

为简化模型表达，且考虑应用时磁场方向多平行于晶体的易磁化轴，应力方向垂直于晶体易磁化轴，假定MSMA 具有各向同性的物理性质。因此，在建立MSMA 简化力学模型时，选用各向同性屈服面作为判断重定向起始的依据，假设在MSMA 应力诱发马氏体重定向、逆重定向过程中起始面方程[31]为：

2.3 MSMA 分段线性化多维本构模型

将式(8)、式(12)、式(13)代入式(11)，可得：

由式(7)、式(10)和式(23)可得：

2.4 MSMA 超弹性效应过程描述

上述本构模型可以反映磁场作用下的MSMA超弹性效应：当H≥Hf(2,1)时，MSMA 在外力作用下，磁场择优取向马氏体变体开始发生弹性变形，当外力增加到某一值时，开始诱发马氏体重定向，即磁场择优取向马氏体变体在外力作用下逐渐转变为应力择优取向马氏体变体，这个过程可以由式(22)来描述；当卸载后，由于外部磁场的存在，应力择优取向马氏体变体在无外力作用时无法稳定存在，这样应力择优曲线马氏体又会自动逐渐转变为磁场择优取向马氏体变体，于是MSMA 又恢复到原来的形状，这个过程可以由式(33)描述。

为判断材料使用弹性本构关系还是塑性本构关系，定义加卸载准则如下：

3 重定向及逆重定向临界应力确定

为研究MSMA 临界应力和磁场的关系，Couch 等先后采用线性函数和多项式函数[26]对不同环境磁场下MSMA 临界应力进行预测。本文在上述研究的基础上，进一步对比分析了MSMA 临界应力和磁场的变化关系，提出采用Logistic 函数作为临界应力和磁场的关系函数，上述函数具体形式见表1。

表1 临界应力-磁场关系函数Table 1 Critical stress magnetic field relation function

利用现有文献中4 组MSMA 的材性试验数据(材料参数见表2)，分别对线性函数、多项式函数和Logistic 函数的关键参数进行拟合。首先，利用4 组试验数据同时对上述3 种函数进行拟合(图3)，随后，分别采用4 组数据对上述3 种函数进行拟合(图4～图7)。采用拟合优度R2作为反映函数与数据拟合效果的参数，其值越接近1，表明拟合效果越好，上述拟合过程得到的R2值见图3～图7中数值，其平均值见表3，对比可见：1)对比图中数据点分布，可见临界应力与磁场大小呈显著的S 形分布，因此采用S 形函数进行拟合更为合理；2) 3 种临界应力-磁场关系函数中，线性函数拟合效果最差，Logistic 函数拟合效果最好，单一材料试验数据拟合时，平均R2值可达0.993，多项式函数拟合效果略差于Logistic 函数；3)由于不同文献中的试验条件和材料略有不同，因此4 组数据同时拟合时的效果要明显差于各组数据分别拟合的结果，Logistic 函数预测的各临界应力平均R2值前者为0.945，后者为0.993。上述对比可见，Logistic 函数用于预测临界应力-磁场关系无论从形式上，还是从精度上都相比其余两个函数更优，拟合后的Logistic 函数各参数取值见表4。

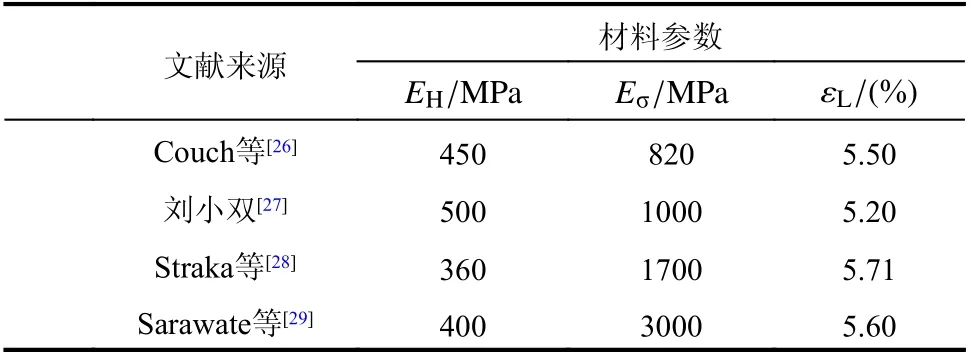
表2 文献试验数据及对应材料参数Table 2 Literature test data and corresponding material parameters

表3 拟合优度R2 平均值Table 3 Average value of goodness of fit R2

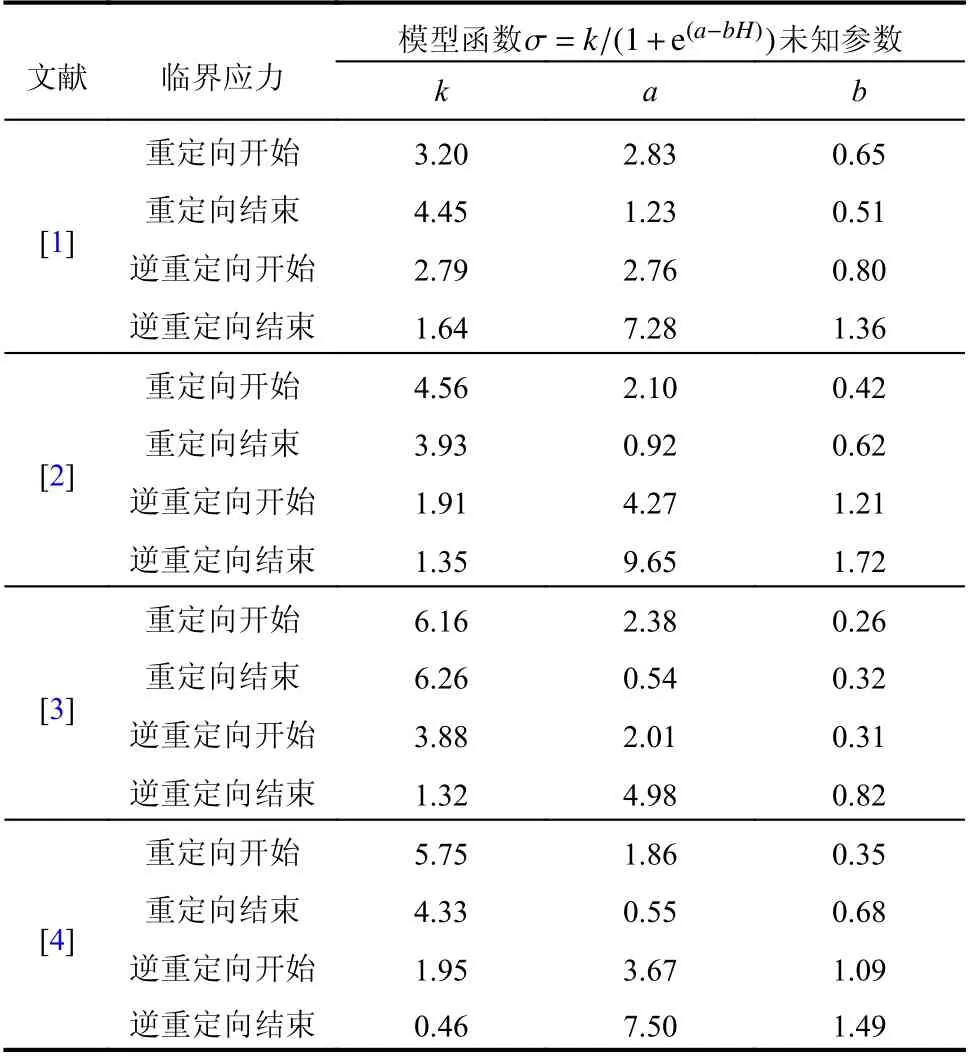
表4 临界应力表达式参数Table 4 Parameters of critical stress expression

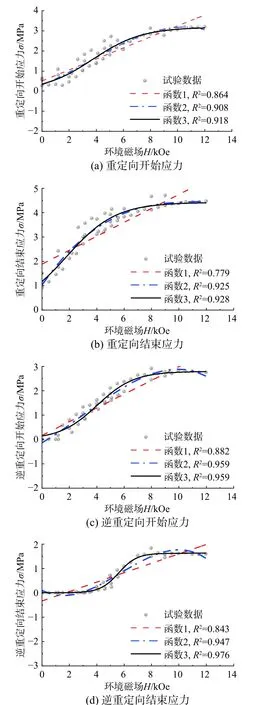
图3 四组试验数据拟合结果Fig. 3 Fitting results of four groups of test data

图4 Couch[26]试验数据拟合结果Fig. 4 The fitting results of Couch[26]

图5 刘小双[27]试验数据拟合结果Fig. 5 The fitting results of Liu[27]

图6 Straka[28]试验数据拟合结果Fig. 6 The fitting results of Straka [28]

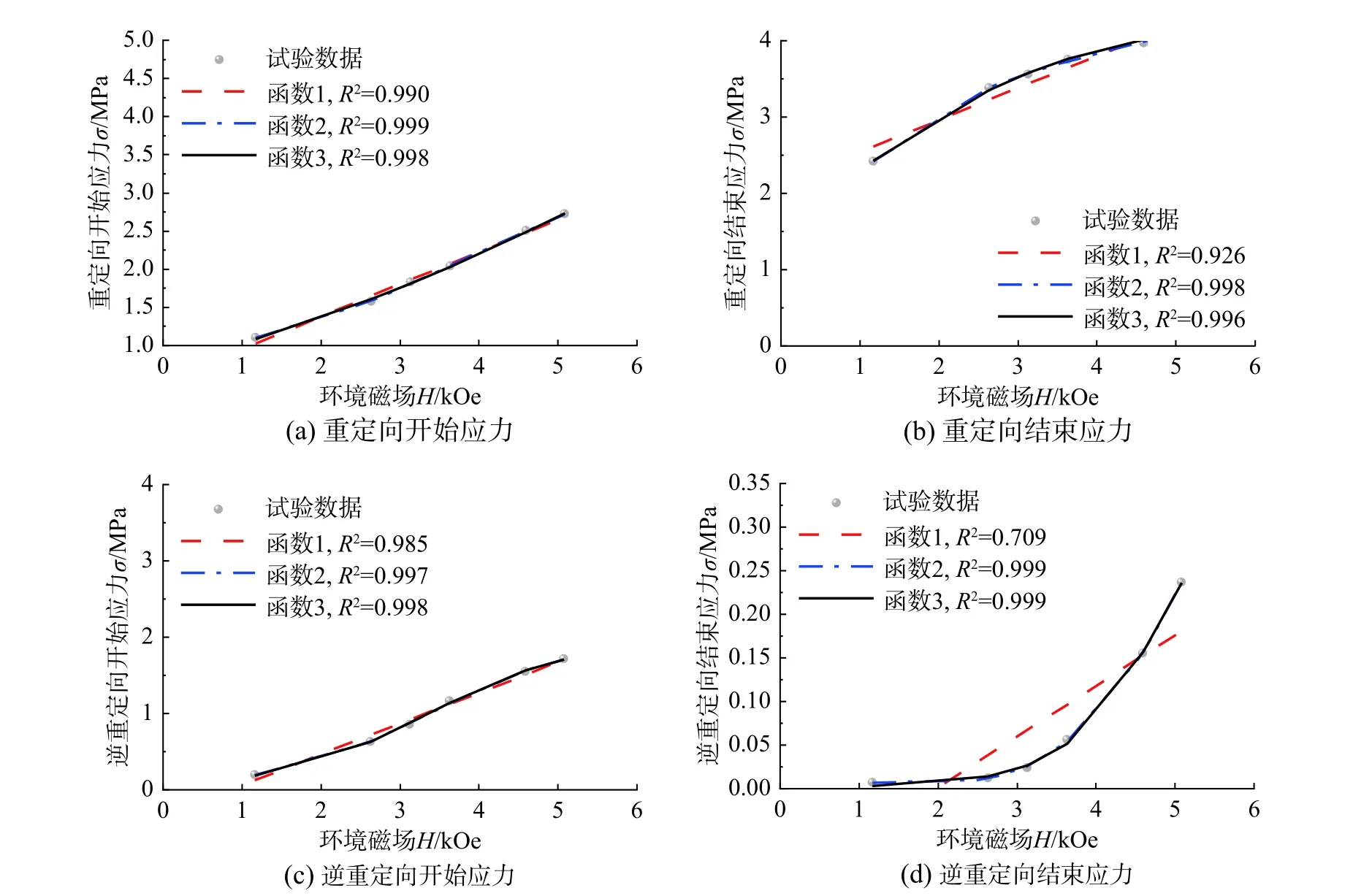
图7 Sarawate[29]试验数据拟合结果Fig. 7 The fitting results of Sarawate[29]

4 模型数值模拟精度对比分析

利用本文第3 节临界应力-磁场关系函数，结合第2 节建立的MSMA 本构模型，根据表2 所给材料参数，计算不同磁场下MSMA 滞回曲线，并与试验结果进行对比，如图8～图11 所示。由图可见，本文所建立模型的滞回曲线与试验所得曲线形一致，马氏体重定向及逆重定向的开始与结束临界应力接近，即该理论模型能较好的描述MSMA的应力-应变关系。

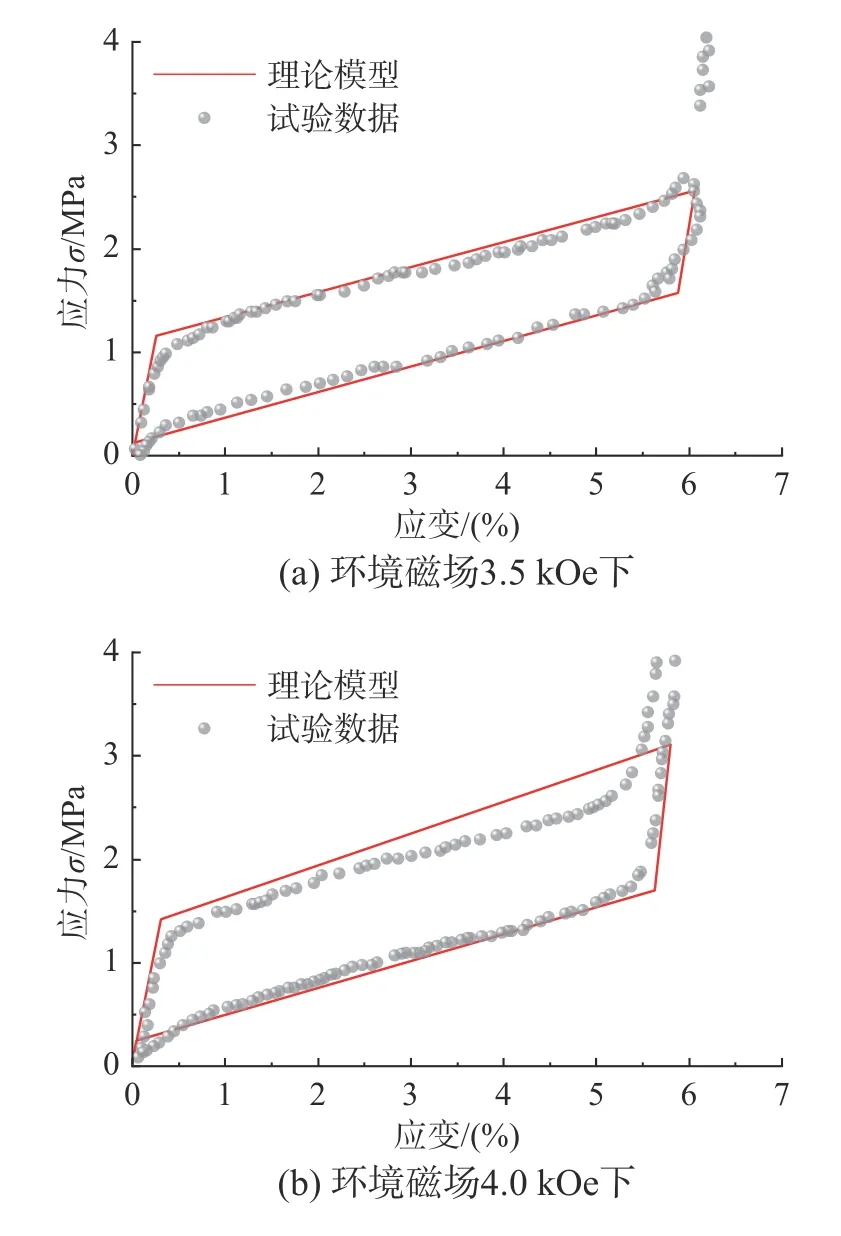
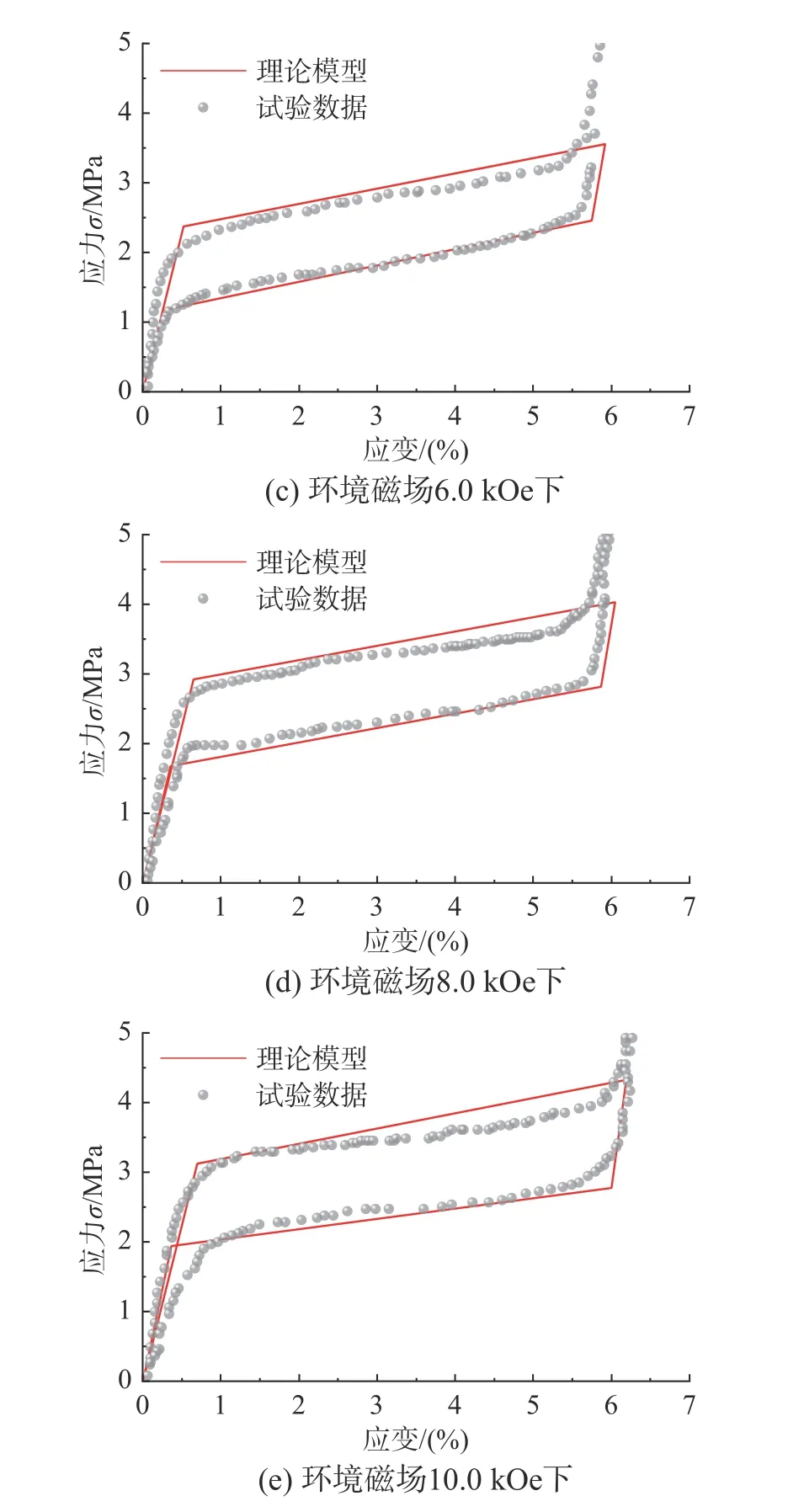
图8 理论模型数值模拟结果与Couch[26]试验值对比Fig. 8 Comparison between numerical simulation results of theoretical model and experimental data in Couch[26]

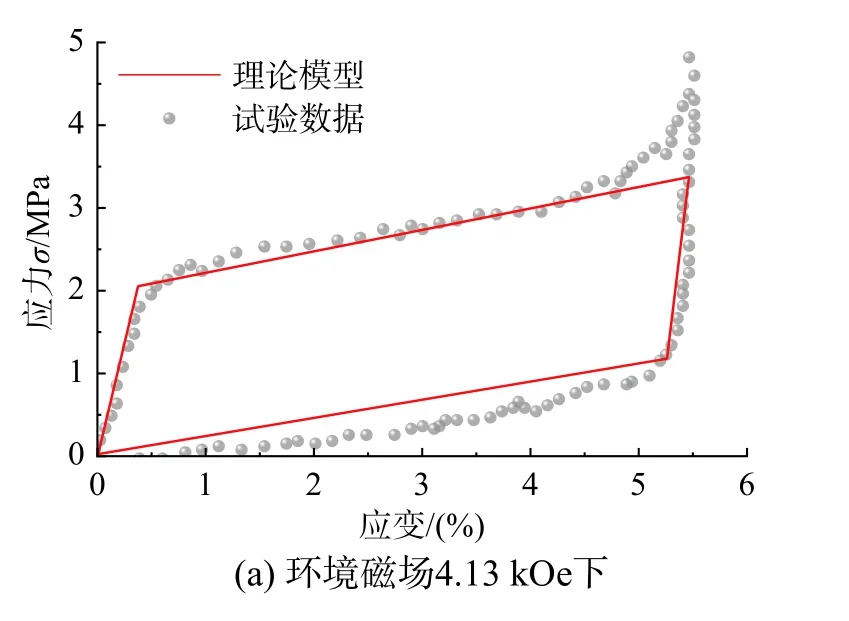
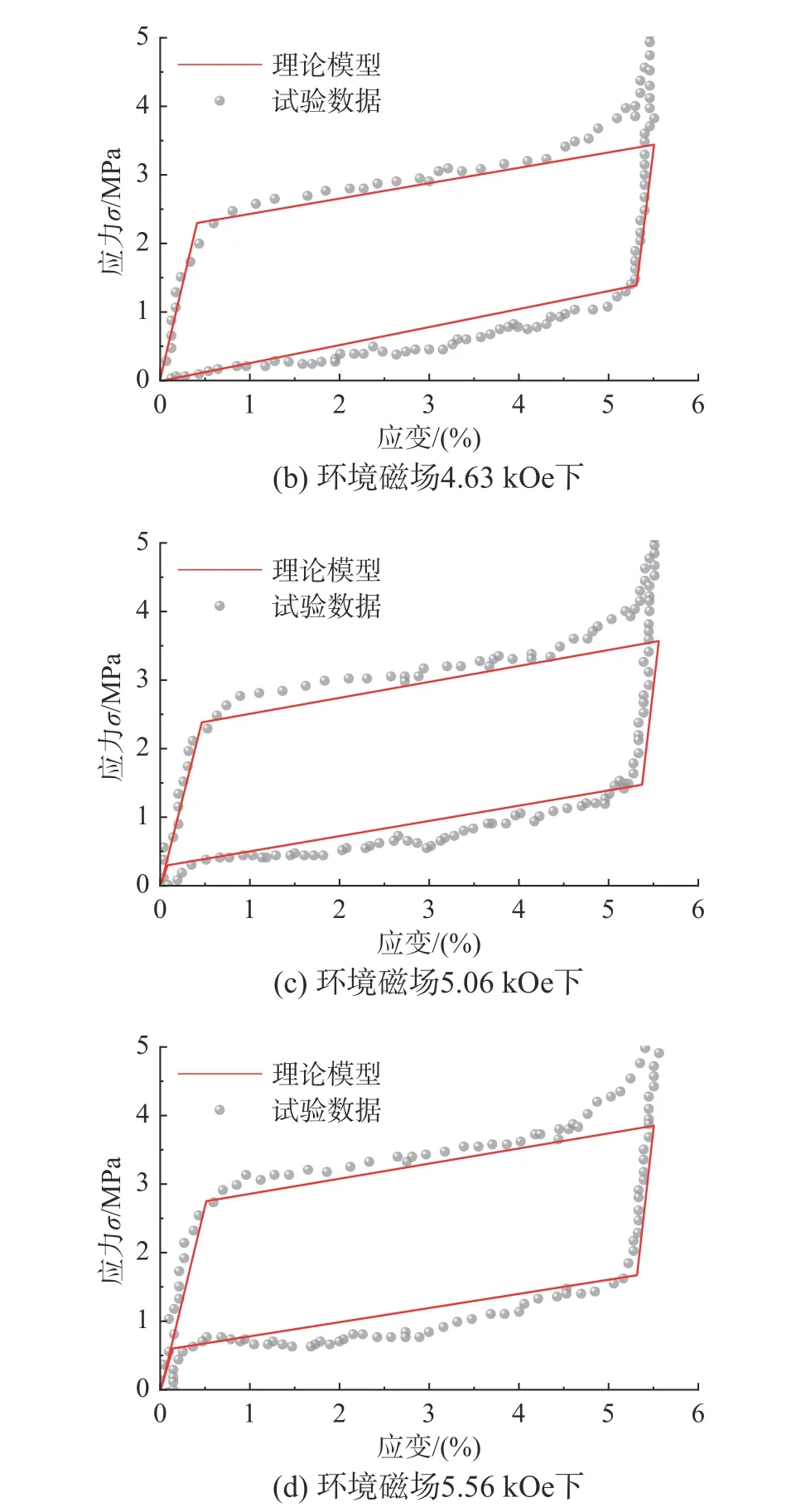
图9 理论模型数值模拟结果与刘小双[27]试验值对比Fig. 9 Comparison between numerical simulation results of theoretical model and experimental data in Liu[27]

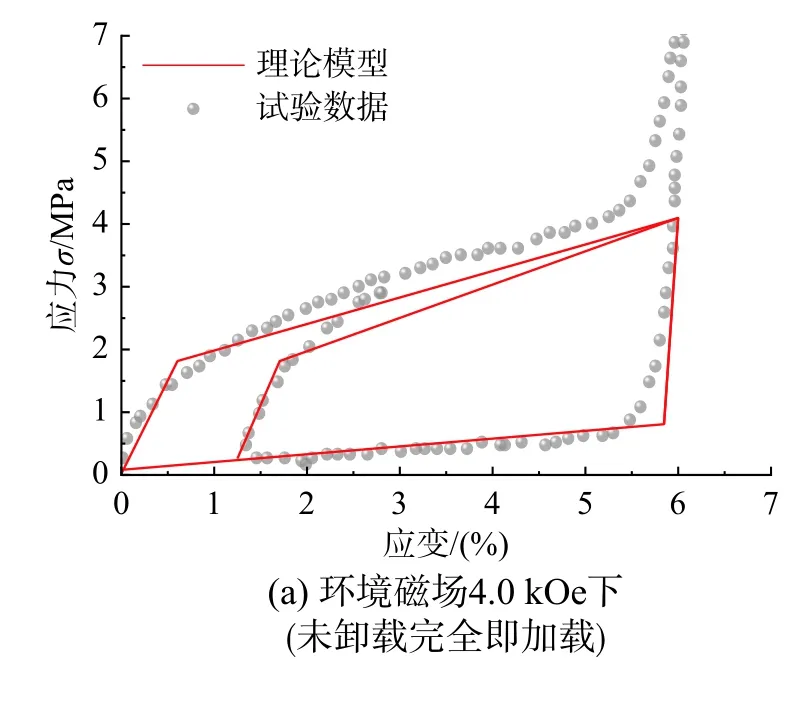
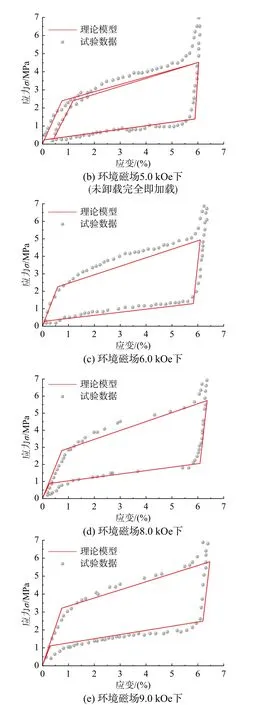
图10 理论模型数值模拟结果与Straka [28]试验值对比Fig. 10 Comparison between numerical simulation results of theoretical model and experimental data in Straka[28]

图11 理论模型数值模拟结果与Sarawate[29]试验值对比Fig. 11 Comparison between numerical simulation results of theoretical model and experimental data in Sarawate[29]

进一步，对比分析了各工况下理论和试验得到的滞回耗能，如图12 所示，对比可见，理论模型与试验结果的滞回耗能较为接近，误差在6.7%～17.1%，该理论模型能够一定程度上预测MSMA的耗能能力。

图12 模型与试验滞回耗能及误差Fig. 12 Hysteretic energy consumptions of model and test

在工程应用，滞回曲线和耗能能力是评价MSMA 特性的关键，故本文所建立的分段线性化本构模型能够满足工程应用的精度要求，且

形式简单直观，参数较少，适于模拟工程应用中考虑磁场影响的复杂应力条件下MSMA 超弹性特性。

5 结论

本文基于经典塑性理论框架，建立了考虑磁场影响的MSMA 分段线性化超弹性本构模型，该模型具有物理概念明确、形式简单、参数少等优点，更适用于工程应用。主要内容和结论如下：

(1)引入应力择优取向马氏体变体体积分数作为内变量，基于塑性理论框架，构建了MSMA 分段线性化超弹性本构模型，该模型能够完成描述不同磁场环境下的MSMA 超弹性效应全过程。

(2)提出了描述马氏体重定向和逆重定向临界应力与环境磁场关系的Logistic 关系函数，拟合结果表明该函数的拟合优度可达0.993，大于线性函数和多项式函数的0.897 和0.990，且在形状上与试验结果更为吻合。

(3)对滞回曲线形状和滞回耗能的数值模拟对比表明，所建立的本构模型能够较好地预测MSMA构件的力-位移关系，且理论滞回耗能与试验的误差平均仅为11.9%，满足工程应用需求。