周期为N≡1(mod4)的平衡最优几乎二元序列对

彭秀平，李红晓，王仕德，林洪彬

（1.燕山大学信息科学与工程学院，河北 秦皇岛 066004；2.河北省信息传输与信号处理重点实验室，河北 秦皇岛 066004；3.燕山大学电气工程学院，河北 秦皇岛 066004)

1 引言

具有优良自相关特性的序列在线性系统参数识别、实时信道估计、均衡和同步等领域都有广泛应用[1]，另外一些应用领域如对抗多径干扰[2]、多载波码分多址（CDMA,code-division multiple access）、正交频分复用多址（OFDMA,orthogonal frequency division multiple access）、雷达和测距系统等不仅要求序列具备优良的自相关特性，也需具备优良的互相关特性[3]。为了给序列设计提供一个理论评判标准，国内外学者对序列设计相关性的理论界限进行了研究[4-6]，其中，Shedd 等[6]推导了周期自相关和互相关的理论界，并在周期自相关值和互相关值之间进行了折中。Sarwate 界表明，不存在一组序列同时具有优良自相关性和优良互相关性以满足不同的应用需求。为此，国内外学者主要致力于先设计自相关旁瓣值尽可能小的各类序列，再研究它们的互相关性。当序列的自相关函数旁瓣值全为0 时，称这样的序列为最佳序列，然而现有的最佳二元序列仅存在长度为4 的情况，最佳四元序列仅存在长度为2、4、8 和16 的情况[7]。基于此，备受关注的是具有理想或优良自相关特性的（几乎）二元[8-9]和（几乎）四元序列[10-11]及最佳多相序列[12-14]的构造方法研究。由于最佳多相序列大量存在，目前研究得到了一些满足Sarwate 界最优的最佳多相序列集[13]。同时，由于二元和四元序列在实际应用中实现简单，学者们对这些具有优良自相关特性的二元[15-16]和四元序列[17]的互相关特性也进行了大量研究，然而这些序列的互相关值并不能达到Sarwate 界的下界值。

为解决上述问题，文献[18]对平衡二元序列对的互相关值的理论界做了进一步研究，以序列自相关值最优为前提研究序列对互相关值的理论界，与Sarwate 界相比，提高了互相关理论下界值，并提出了周期为N≡1(mod4)的自相关值为{1,-3 }且满足理论界的下界值为的平衡最优二元序列对的构造方法。在此思想的启发下，文献[19]对自相关模值为且周期为N≡1(mod4)的平衡四元序列对的互相关理论界进行了研究，并得到了满足理论界要求的理想四元序列对；文献[20]从另一角度进行了研究，当二元序列对的互相关值满足最优值情况时，对周期为N≡1(mod4)且以互相关值{1,-3}为前提，对这类序列对的自相关理论界进行了研究，并得到了满足自相关理论下界值的最优二元序列对的构造方法，但是得到的最优二元序列对相当有限，在周期N≤300内，仅存在N=5,37,101,197这4 种情况。

为了获得更多的最优二元序列对，本文在文献[20]的基础上，通过在二元序列中引入一个0 元素，首先对（几乎）二元序列对的互相关值和自相关值的取值情况进行了讨论，得出最大互相关值θ c分别为1、2、3 这3 种情况；其次以互相关值最优（即θc=1,2）或几乎最优（即θc=3）的分布值情况为前提，推导出周期为N≡1(mod4)的平衡几乎二元序列对的自相关函数值所满足的理论界；最后基于四阶分圆类的方法，提出了满足（几乎）最优互相关值和自相关理论界下界值的平衡（几乎）最优几乎二元序列对的构造方法。

2 基本概念及引理

定义1若周期为N的序列满足式(1)。

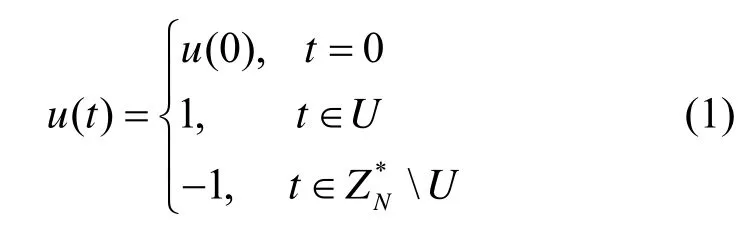
为了便于描述，本文约定只考虑u(0)=-1 的情况，那么集合称为二元序列u的特征集，集合称为几乎二元序列u'的特征集。序列u和u'分别称为集合U和U'的特征序列。

对于二元序列，如果N是奇数，则u是平衡的；对于几乎二元序列，如果N是奇数,则u'是平衡的。

定义2令u′和v′是2 个周期为N的几乎二元序列，则序列对u′和v′的周期互相关函数定义为

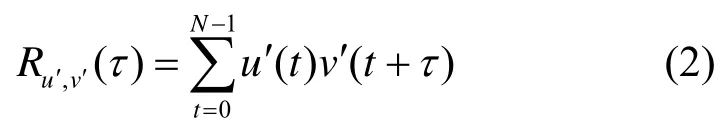
定义 3令θc为序列u′和v′的最大互相关幅度值，θ a为序列u′和v′的最大异相自相关幅度值，分别定义为

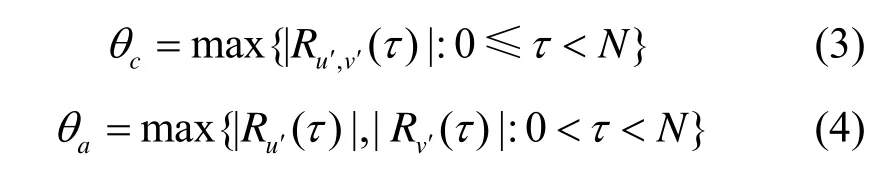
定义4令Ni表示序列u′和v′互相关取值为i时的数量，定义为

定义5设N=4f+1为奇素数，α是有限域GF(N)上的本原元，令

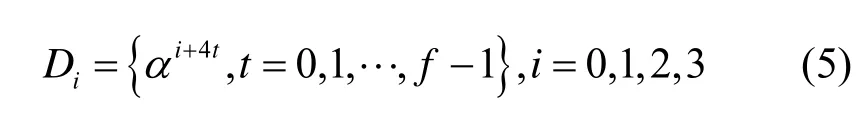
则称Di为GF(N)上的四阶分圆类。令

其中，Di+1代表集合代表和模N，则称（i,j）为基于GF(N)的四阶分圆数。

引理1[21]设N=4f+1为奇素数，其中f为正整数。N又可表示为N=4y2+x2，根据f的奇偶性和x≡1(mod4)或x≡3(mod4)的不同取值将四阶分圆数进行如下分类。

当f为奇数时，Z N上的四阶分圆数的关系如式(7)所示，ZN四阶分圆类的5 个基本分圆数如表1 所示。

表1 f 为奇数时，Z N四阶分圆类的5 个基本分圆数

当f为偶数时，Z N上的四阶分圆数的关系如式(8)所示，四阶分圆类的5 个基本分圆数如表2 所示。

表2 f 为偶数时，ZN四阶分圆类的5 个基本分圆数

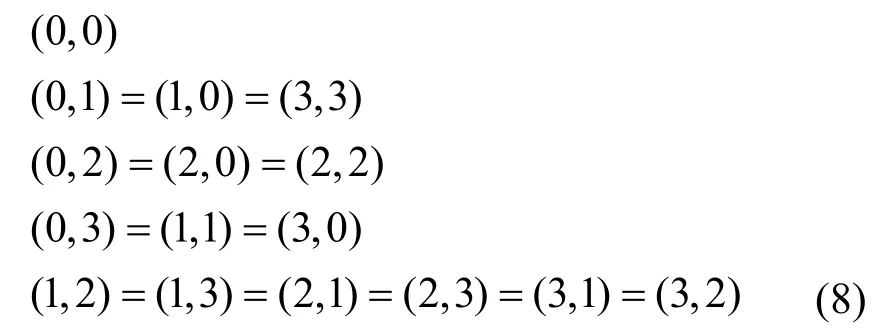
引理2[22]对于素数N=4f+1，则分圆数和式满足

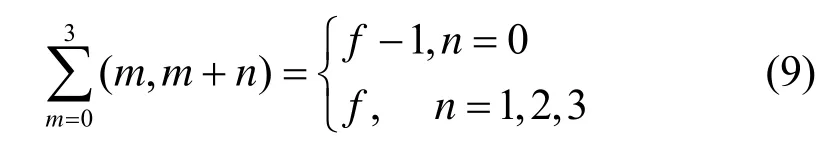
3 平衡（几乎）二元序列的相关界限

引入一个0 元素后，新生成的几乎二元序列对的相关值会发生变化，所以本节首先对（几乎）二元序列对的互相关值和几乎二元序列的自相关值进行证明。

引理3 令N≡1(mod4)，当u′和v′为周期为N的平衡几乎二元序列时，互相关值有以下3 种情况：3(mod4)。

证明令和v′的互相关函数值可以计算为

证明当u′=v′时，引理5 是引理3 的特殊情况，根据引理3 可知引理5 结论成立。证毕。

通过引理3 可知，当2 条序列都为平衡几乎二元序列时，2 条序列的最大互相关值的最小值为θc=1，这时称平衡几乎二元序列对为平衡最优互相关的I 型−几乎二元序列对。为了获取更多满足应用需求的几乎二元序列对，本文对θc=3的平衡几乎二元序列对的理论界及构造方法进行了研究，这时称平衡几乎二元序列对为平衡几乎最优互相关的I 型−几乎二元序列对。通过引理4 可知，当一条序列为平衡几乎二元序列，另一条序列为平衡二元序列时，2 条序列的最大互相关值θc的最小值为θc=2，这时称平衡几乎二元序列对为平衡最优互相关的II型−几乎二元序列对。

本文将采用式(10)和式(11)[23]证明θa的下界值。

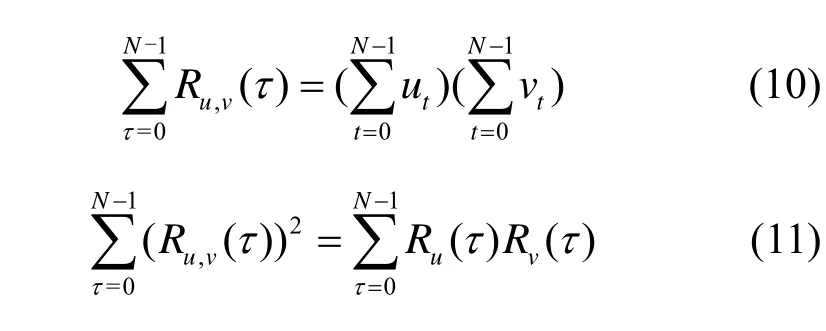
引理6设u'和v'是几乎二元序列，u是二元序列，且u'、v'和u均为周期为N≡（1 mod4)的平衡序列，则具有平衡最优或平衡几乎最优互相关的I 型−几乎二元序列对和具有平衡最优互相关的II型−几乎二元序列对的互相关值的分布情况如表3所示。

表3 几乎二元序列对的互相关值分布情况

其他情况可按类似方法分析得到。证毕。

接下来，基于表3 中列出的3 种类型的具有平衡（几乎）最优互相关的几乎二元序列对互相关函数值及其分布情况，分别给出3 种类型的几乎二元序列的自相关函数理论界。

定理1设u′和v′是周期为N≡1(mod4)且具有最优互相关的平衡I 型−几乎二元序列对，即θc=1，则序列u′和v′的最大异相自相关幅值满足

证明 定理3 的证明与定理1 证明类似。

定义6 设u′和v′是几乎二元序列，u是二元序列，且u′、v′和u均为周期为N≡（1 mod4)的平衡序列，当u′和v′为具有最优互相关的平衡I 型−几乎二元序列对且θa满足式(12)下界值时，称u′和v′为平衡最优几乎二元序列对。当u和v′为具有最优互相关的平衡II 型−几乎二元序列对且θ a满足式(16)下界时，称u和v′为平衡最优几乎二元序列对。当u′和v′为具有几乎最优互相关平衡I 型−几乎二元序列对且θ a满足式(17)下界值时，称u′和v'为平衡几乎最优几乎二元序列对。

4 平衡 (几乎)最优几乎二元序列对构造

本节将分别给出满足定义6 的周期为素数N=4f+1的平衡最优几乎二元序列对和平衡几乎最优几乎二元序列对的构造方法。

定理4令为一奇素数，其中，f为整数，y为整数 。当几乎二元序列对u′和v′、u′和v、u和v′的其他参数满足表4 所示要求时，得到的序列对为平衡最优几乎二元序列对或平衡几乎最优几乎二元序列对。

表4 满足条件的平衡(几乎)最优几乎二元序列对

证明以f为奇数，x=1，特征集合的平衡几乎二元序列对为例进行证明。首先考虑u′和v′的互相关，当τ=0时，容易得到Ru′,v′(0)=0。当τ≠ 0时，存在一个整数k(0≤k＜4)，使τ∈Dk，由于u′(0)v′(τ)+v′(0)u(N-τ)=0，则

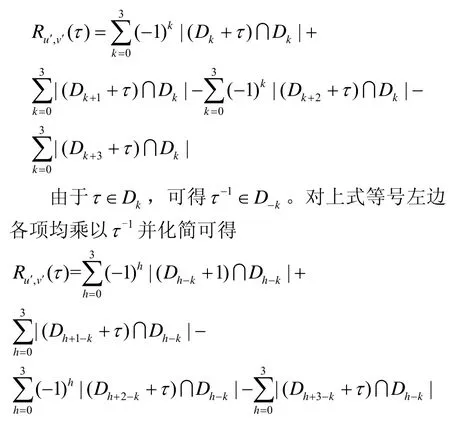
根据分圆数的定义（见式(6)），将上式转换成分圆数的形式，并根据引理2 进行化简可得

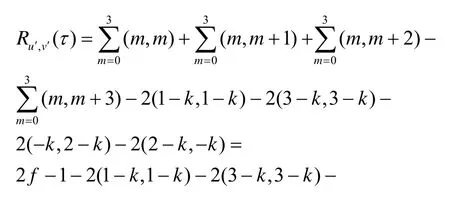
与计算u′和v′的互相关函数值方法类似，可得u′和v′的自相关函数值分别为

类似地，当x=-1 时，也可得到u′和v′为平衡最优几乎二元序列对；当x=±3 时,u′和v′为平衡几乎最优几乎二元序列对；当取x=1时，u′和v或u和v′为平衡最优几乎二元序列对。

显然，当N=37时有θc=1和θa=7满足引理6的要求和定理1 的下界值，可知得到的序列对u′和v′为平衡最优几乎二元序列对。而对于相同周期长度，通过文献[20]的方法得到θc=3和θa=7，可知在相同θ a值情况下本文得到的序列对的θ c更小。

当N=37，u′ 和v的特征 集合分别为U′=D0∪D1，V=D0∪D3时，可得θc=2，θa=7满足引理6 的要求和定理2 的下界值，所以序列对u′和v为平衡最优几乎二元序列对。同样与文献[20]中方法得到的最优二元序列对相比，在相同θ a值情况下本文得到的序列对的θ c更小。

当N=13，u′和v′的特征集合为U′=D0∪D1，V'=D0∪D3时，可得θc=3，θa=3，满足引理6 的要求和定理3 的下界值，所以u′和v′为平衡几乎最优几乎二元序列对。其互相关最大值虽然与文献[20]提出的界限相同，但是不再限定f为奇数，拓宽了最优序列对的存在空间。

5 结束语

本文通过在二元序列基础上引入一个0 元素的方式，首先对周期为N≡1(mod4)的两类（几乎）二元序列对的互相关函数值的最小值进行了研究，然后在此互相关值基础上，对序列对中序列的自相关值的理论界进行了研究，最后基于四阶分圆类，构造了4 对满足定理1～定理3 中理论界下界值的周期为N≡1(mod4)的平衡（几乎）最优相关特性的几乎二元序列对。表5 列出了本文与目前已有的平衡最优二元序列对在性能参数方面的对比情况。由表5可知，与文献[18]相比，文献[18]是在序列具有最优自相关的前提下得到了序列对互相关满足的理论界。与文献[20]相比，虽然文献[20]满足最优二元序列对的理论界，但是限定f为奇数，导致存在空间相当有限，在N≤300内仅存在周期为N=5,37,101,197这4 种情况，而本文将f的取值扩展到任意整数可得到更多满足理论界的序列对，同样在N≤300的范围内，本文可得到的平衡（几乎）最优序列对周期为N=5,13,17,37,73,101,109,197,257这9 种情况，拓宽了序列存在空间。在文献[20]中，只构造了满足θc=3的序列对，而在本文中，构造了θc=1、θc=2和θc=3的3 种几乎二元序列对，进一步改善了序列相关性的同时也为实际工程应用和通信系统提供了更多的可供选择的序列对。

表5 现有的平衡（几乎）最优几乎二元序列对的比较