基于分解集成方法的空中交通流量短期预测

王 飞， 孙鹏飞

(中国民航大学空中交通管理学院， 天津 300300)

随着中国社会的进步与民航事业的发展，航班量持续增加，空域资源日益紧张，空管的协调压力持续增大，为了缓解空域拥挤和降低管制员的负荷，需要对空中交通流进行优化和管理。流量预测是空中交通管理的重要内容，流量预测一般分为中长期预测与短期预测，中长期预测可以为航空公司运营调整、机场建设和改造提供参考，流量短期预测可以为管制员提供辅助决策信息，对优化交通流和减少延误更具现实意义。因此，对空中交通流量进行短期预测是很有必要的。

目前中外学者对空中交通流量短期预测的主要研究方法有：①基于飞行计划的预测方法，该方法简单易行，但在航路飞行时，不确定因素较多，预测精度较差，并且航班量巨大时，运算较为复杂，速度较慢；②基于数理统计的预测方法，主要考虑了空中交通流的线性特征，操作较为简便，但对非线性因素考虑不足，具有局限性；③智能预测方法，具有较强的自学习能力、适应性和鲁棒性，可以在大量的数据中挖掘出复杂的数据关系，但数据较少时无法准确地获取数据的特征，预测效果较差；④基于非线性混沌理论的预测方法，该方法要求非常恰当的重构系统相空间，但相空间重构参数难以准确确定，主观性较强。

空中交通流已被证实具有复杂的非线性特征，杨阳[1]对空域扇区流量时间序列具备混沌特性进行了验证，王飞[2]对短期空中交通流的时间序列进行了非线性检验，验证了5 min时间尺度的空中交通流时间序列是非线性的。

针对空中交通非线性系统，传统方法在刻画内部结构、揭示演化机理、预测发展趋势等方面存在结构性瓶颈；由于空中交通流容易受到天气和人为等因素的影响，具有较强的非线性，利用单一方法直接进行预测时，难以取得较好的预测效果。分解集成方法自提出以来，在复杂非线性系统应用方面显示出良好的应用前景。分解集成方法在空中交通流预测领域的研究处于起步阶段，但该方法在股票、油价、电力预测等领域均有应用，尤其是地面交通领域的研究成果可为空中交通流量短期预测提供借鉴。贺毅岳等[3]提出了经验模态分解下基于支持向量回归的股票价格集成预测方法(empirical mode decomposition and SVR based stock price integrated forecasting，EMD-SVRF)，实现了对非平稳、非线性股票价格时间序列的高精度预测。汪子述[4]构建了基于数据特征驱动重构的分解集成模型，并通过对原油价格进行预测，证明了该模型具有更高的预测准确度和更少的预测时间。周程等[5]提出了一种基于趋势分解和小波变换的多重“分解-集成”预测方法，利用趋势分解将货运量分解为趋势项和非趋势项，通过小波分解将非趋势项进一步分解成低频项和高频项，分别建立预测模型，选用相加集成得到货运量预测值，降低了问题复杂度，有效提高了预测性能。Wang等[6]提出了一种EMD-ARIMA(empirical mode decomposition and autoregressive integrated moving average)组合模型，对5～20 min内的高速公路车辆速度进行了预测，并将EMD-ARIMA组合模型与差分自回归移动平均模型(autoregressive integrated moving average, ARIMA)，人工神经网络(artificial neural network, ANN)等传统预测方法进行比较，发现提出的组合预测模型结果更好。Majumder等[7]提出了一种基于变分模态分解(variational mode decomposition, VMD)和新内核极限学习机的组合预测模型，用于太阳能辐射的预测，与其他模型作比较，有更高的预测精度。

为了对空中交通流量进行短期预测，现提出基于分解集成方法的组合预测模型。首先，对流量时序数据进行集合经验模态分解，得到若干分量，通过复杂度检验将这些分量分为高频和低频，高频的分量采用BP(back propagation)神经网络进行预测，低频的分量使用最小二乘法进行预测。最后对各分量预测的结果采用线性加和进行集成预测，得到最终的预测结果。

1 分解与预测方法

1.1 集合经验模态分解

经典模态分解(empirical mode decomposition，EMD)是一种自适应信号时频处理方法，此方法可以根据数据的时间尺度特征进行分解，非常适用于非线性数据的处理[8]。但EMD分解存在着模态混叠问题，集合经验模态分解(ensemble empirical mode decomposition,EEMD)可有效克服这个问题[9]。

EEMD分解的具体步骤如下。

Step 1将白噪声ω(t)加入到原信号X(t)里得到信号Y(t)，表示为

Y(t)=X(t)+ω(t)

(1)

Step 2对信号Y(t)进行EMD分解，得到n个模态分量ci(t)和一个残差r(t)，表示为

(2)

Step 3重复Step 1、Step 2m次，对信号Y(t)加入不同的白噪声，得到m组模态分量和m个残差。根据文献[8]，所添加的白噪声应符合关系式

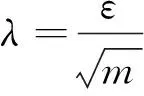
(3)

式(3)中：λ为输入信号与经过EEMD分解后分量加和的误差；ε为所加白噪声的幅值系数；m为添加白噪声的次数。

Step 4对得到的数据求均值，得到最终的n个模态分量imfi(t)和一个残差res(t)，即

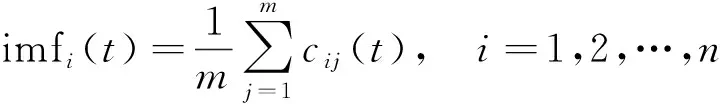
(4)

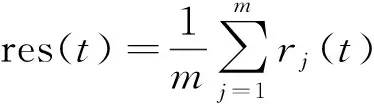
(5)

1.2 BP神经网络

BP神经网络是一种采用误差反向传播算法的神经网络，它在结构上分为输入层、隐含层和输出层，如图1所示。

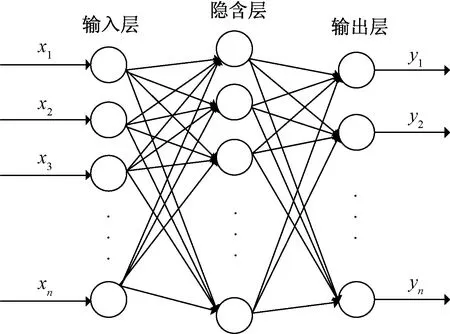
图1 BP神经网络的结构Fig.1 The structure of BP neural network

BP神经网络进行训练时，具体步骤如下。

Stpe 1信息正向传播。信息从输入层传递到隐含层，再传递到输出层，隐含层神经元的输入ui为

(6)

式(6)中：n为输入层节点数；wij为输入层节点j与隐含层节点i之间的权重；xj为输入层节点；a1i为隐含层节点i的阈值。

隐含层神经元的输出pi为

(7)

式(7)中：f为隐含层的传递函数。

输出层神经元的输入qk为

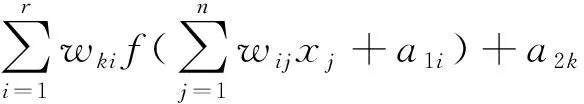
(8)

式(8)中：r为隐含层的节点数；wki为隐藏层节点i与输出层节点k之间的权重；a2k为输出层节点k的阈值。

输出层神经元的输出yk为

(9)

式(9)中：φ为输出层的传递函数。

Step 2误差反向传播。得到训练的结果后与实际的数据进行比对，计算得到训练数据与实际数据的误差E为

(10)

式(10)中：m为输出层节点的数量；Tk为输出层节点k的期望输出值。

利用误差去调整权值和阈值，使误差沿梯度方向下降，经过多次迭代后，得到误差最小的权值和阈值，停止训练。

1.3 最小二乘法

最小二乘法(ordinary least squares, OLS)是一种拟合算法，它通过寻找最小化误差的平方和拟合曲线，是一种简便的线性拟合方法。以直线拟合的例子讲解最小二乘法的原理。最小二乘法拟合的原理如下。

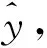
(11)

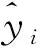
(12)

为了求得Q的最小值，将Q对a0和a1分别求偏导，即

(13)

(14)

进而可计算得到a0、a1，即

(15)

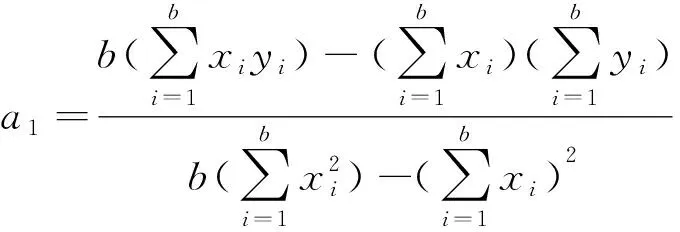
(16)

2 算例仿真

2.1 数据来源

数据来源于三亚4号扇区2017年9月2—19日共计18 d时间尺度为30 min的流量数据，如图2所示，将前17 d的数据作为训练数据，第18天前12 h的数据对预测模型的预测效果进行验证。

图2 原始交通流时间序列Fig.2 Original traffic flow time series

2.2 评价指标

为了评估预测模型性能，选择了均方根误差(root mean squared error，RMSE)；平均绝对误差(mean absolute error，MAE)；均等系数(equal coefficient，EC)作为评价指标，计算公式为

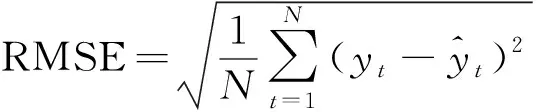
(17)

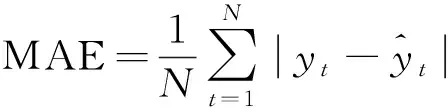
(18)

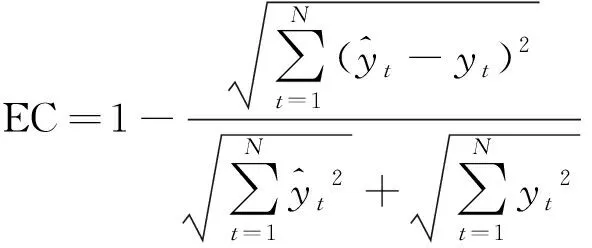
(19)

2.3 数据预测

首先对18 d共计432 h的流量数据进行EEMD分解，根据文献[9]的研究，添加白噪声的次数为100时，白噪声的幅值系数取0.01～0.5较为适宜。经过尝试比较后，设置添加白噪声的次数为100，白噪声的幅值系数为0.1，经过分解后得到模态分量imfi(t)(i=1,2,…,8)与残差res(t)，如图3所示。

图3 EEMD分解后的分量Fig.3 The component value after EEMD decomposition

通过复杂度检验可以确定高复杂度与低复杂度分量，大于0.5的分量被认为具有高复杂度，小于0.5的具有低复杂度[4]。针对不同复杂度的分量采用不同的方法进行预测，可以降低运算时间，提高预测准确度。通过计算排列熵来确定分量的复杂度，使用平均互信息估计相空间重构的延迟时间，使用虚假最近邻点算法估计相空间重构的嵌入维数，并对排列熵归一化处理，得到最终的排列熵。设置阈值为0.5，大于0.5的定义为高频分量，小于0.5的定义为低频分量，如表1所示。

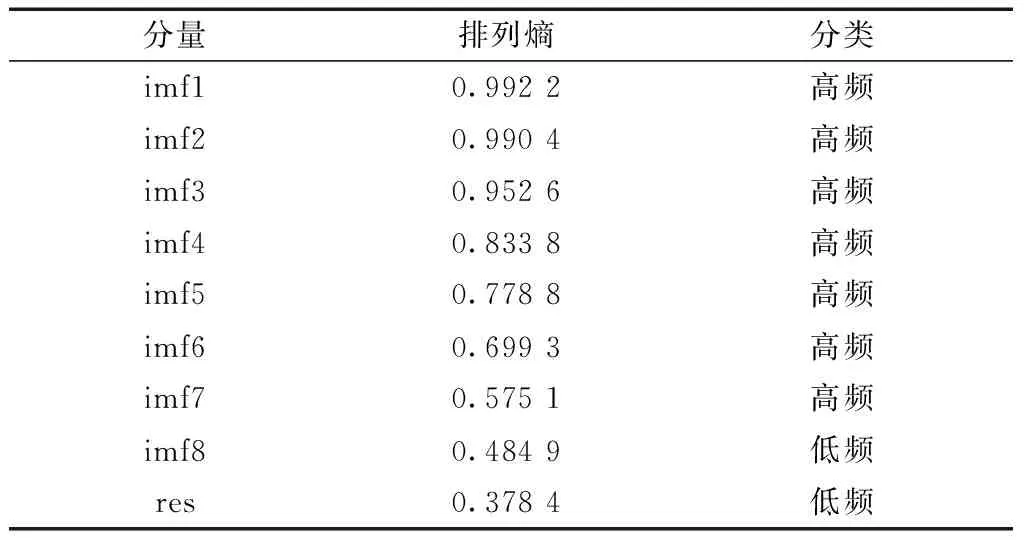
表1 各分量的排列熵

为了更好地验证模型的预测效果，取各分量前17 d共计408 h的数据ai(其中i为天数，i=1,2,…,17)作为训练集。取第18天前12 h的数据b18作为验证集。

BP神经网络具有良好的非线性映射能力和自学习能力，由于高频分量的复杂度较高，预测难度较大，所以对于高频分量，采用BP神经网络进行预测。设置训练次数为5 000次，收敛误差为10-7，权值的学习算法设置为trainlm，选择ai(i=1,2,…,16)作为训练集上的输入，设置输入层节点数为16，选择a17作为训练集上的输出，设置输出层的节点数为1。目前，隐含层节点数的设定还没有一套系统的方法，通常是通过一系列试算确定[10]。通过试算确定了imfi(t)(i=1,2,…,7)的隐含层节点个数为8、5、5、5、3、3、3。

最小二乘法是一种简便的线性拟合算法，具有计算快速的优点。由于低频分量的复杂度较低，采用最小二乘法进行拟合，可以降低计算成本，减少预测的时间。通过多次实验后确定imf8和res拟合多项式的次数为4和6。最后依次进行了预测，如图4所示。

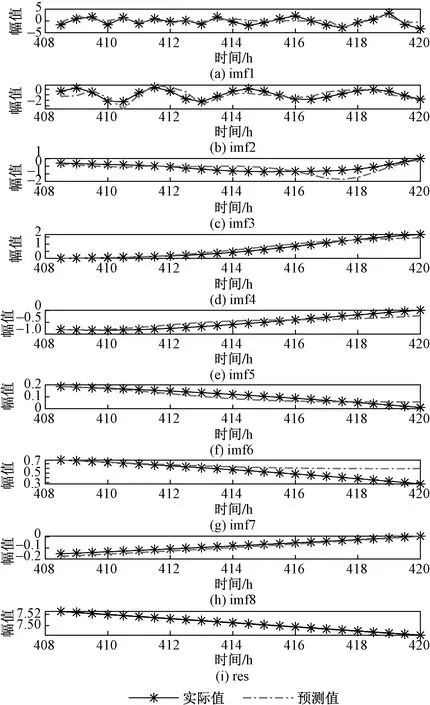
图4 各分量实际值与预测值的对比Fig.4 Comparison of actual and predicted values of each component

为了进一步对模型预测效果进行分析，计算了各分量预测模型的评价指标，如表2所示。

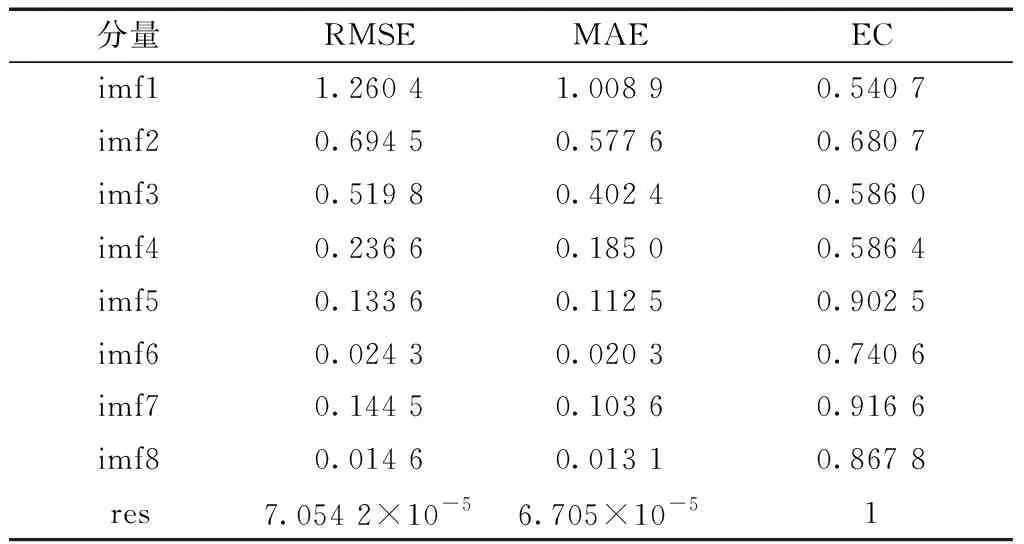
表2 各分量的评价指标值

(20)

计算本文模型预测数据的评价指标，如表3所示。

表3 EEMD-BP-OLS的评价指标值

经过分析发现，本文中预测模型在1～6 h的RMSE值和MAE值均比7～12 h的值小，在1～6 h的EC值为0.905 0，大于7～12 h的0.840 8，说明本模型在1～6 h的预测精度要比7～12 h的高。

2.4 不同方法预测结果对比

为了更好地验证本文组合模型的性能，选取了EMD-BP-OLS模型，BP神经网络模型进行预测，如图5所示(30 min尺度)。

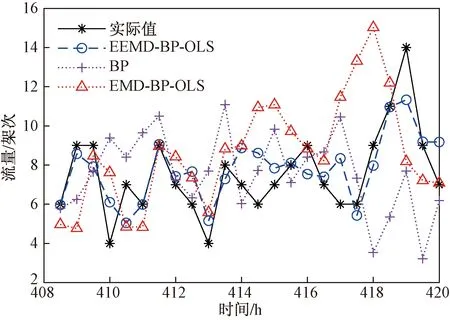
图5 各模型的预测值Fig.5 Predicted values of each model

为了进一步比较不同模型的预测性能，计算了各模型的评价指标，如表4所示。

表4 各模型的评价指标值

分析发现，本文中EEMD-BP-OLS模型相对于EMD-BP-OLS模型和BP模型，RMSE值和MAE值更小，EC值为0.853 2，大于其他两个模型。而EMD-BP-OLS模型相对于BP模型，RMSE值，MAE值相差不大， EC值为0.807 6，要小于BP模型的EC值，说明选择合适的分解方法直接影响预测效果。

2.5 不同时间尺度预测结果对比

为了更好地研究不同时间尺度对本文预测模型的影响，选取了15 min和60 min时间尺度的数据进行预测，如图6所示。

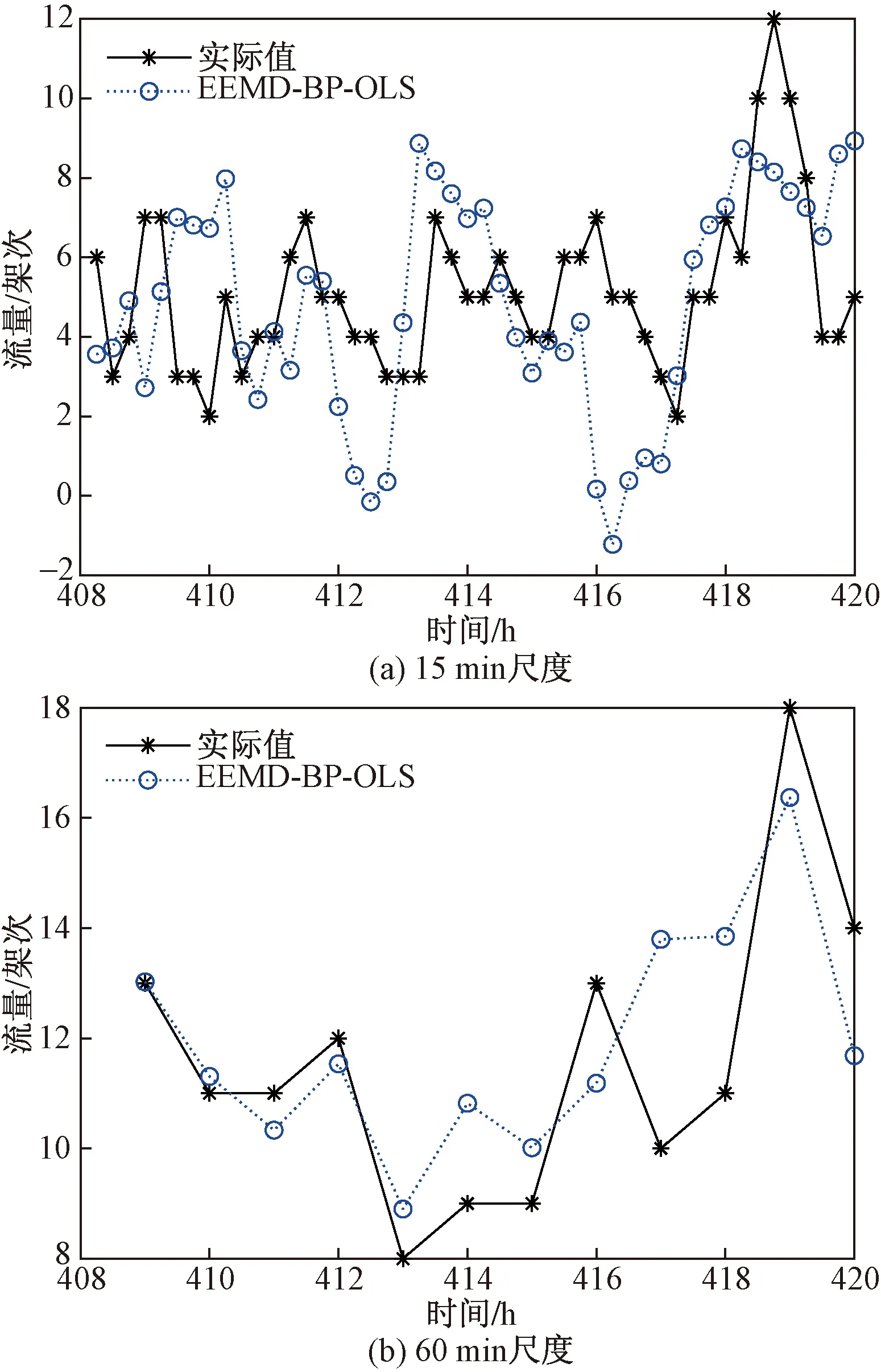
图6 不同时间尺度预测结果对比Fig.6 Predicted values comparison of different time scale

为了更好地分析时间尺度对预测精度的影响，计算了不同尺度下的评价指标，如表5所示。

表5 各尺度的评价指标值

经过分析发现，15 min时间尺度的预测准确度较低，甚至出现了负值，EC值最小，为0.737 6，60 min时间尺度的EC值最大，为0.924 0。由于空中交通易受天气、人为干扰等随机因素影响，在15 min统计尺度的流量数据上体现更为明显，波动性较大，因此难以准确预测。统计尺度越大，部分的随机因素影响会被抵消，更有利于预测。

3 结论

利用基于分解集成方法的组合预测模型对空中交通流量进行短期预测，结果显示：本文模型在1～6 h的RMSE值和MAE值均小于其在7～12 h上的，且1～6 h的EC值更大，达到了0.905 0，说明本文模型在1～6 h预测的精度更高，更适应于短期流量的预测。这一结果也符合空中交通流具有混沌、分形特征，短期预测的准确性是能够得到保障的；通过比较不同的预测模型，本文提出的预测模型精度更高，误差更小，EC值为0.864 7，说明本文的分解集成方法可以充分提取数据的特征信息，降低了数据的复杂度。针对不同特征的分量采用不同的算法进行预测，充分体现了“分而治之”的思想，提高了预测的精度。而EMD-BP-OLS模型相对于BP模型RMSE值和MAE值相差不大，且EC值更小，说明需要根据实际情况合理选择分解方法；通过比较不同时间尺度的预测结果，发现60 min时间尺度的EC值最高，达到0.924 0，准确度较高，其次是30 min时间尺度，为0.864 7，15 min时间尺度最低，只有0.737 6，误差较大，说明本文的预测模型更适合用于30 min和60 min时间尺度的流量短期预测。