基于时间序列模型的青藏铁路路基变形预测

陈卫雄

(中铁十二局集团铁路养护工程有限公司, 拉萨 250014)

青藏铁路沿线经过的多年冻土区地质条件十分复杂,不良冻土现象发育,至青藏铁路2001年修建时，穿越多年冻土区约为546.4 km,其中高温极不稳定区和高温不稳定区长274.25 km，低温基本稳定区和低温稳定区长170.48 km，融区长101.68 km。在所有冻土区线路中，高含冰量地段223.16 km，低含冰量地段221.57 km。

在青藏高原多年冻土区，多年冻土表对岩土工程的稳定性有显著影响。热边界和土壤性质是影响多年冻土表的关键因素。复杂的地质环境和人类活动会导致热边界和土壤性质的不确定性[1]。冻土对路基高程的影响主要体现在，由于温度和承载力的变化，达到了路基强度、变形的协调条件，本质上是水、热、力、变形的耦合作用。其对路基变形的形象，大大威胁了路基的安全性与稳定性。青藏铁路沿线已出现如K1401+888桥7号墩梁缝挤死、K1159+833格台限位块开裂、K1260+821第5片梁格端抗震桩拔起、K0973+551格台垫石裂缝等危险状况。

由于冻土问题的复杂性，带来问题的严重性，近年有诸多学者展开了对铁路冻土融沉、冻胀等的预测研究[2-9]。其中，苗姜龙[3]与祁长青等[4]基于BP(back propagation)神经网络方法，建立了多变形因素的预测模型，并采用COMSOL数值模拟软件进行二次开发。杨笑男[5]采用层次分析的方法，依托GIS(geographic information system)技术进行地质灾害危险性的评级与预测。Chen等[8]引入了人工神经网络(artificial neural network,ANN)和长短期记忆((long short-term memory, LSTM)网络两种基于深度学习技术的模型来预测铁路路基冻胀变形。由于随时间变化，温度随之改变，将会对路基造成影响，王文等[10]基于事件概率回归估计，对青藏铁路沿线平均最高最低气温变化趋势进行了预测与概率估计。李栋梁等[11]预测了青藏高原及铁路沿线未来50年平均最低、最高和年地表温度。此外，常斌等[12]应用神经网络预测模型对青藏铁路沿线冻土通风管路基温度场进行了分析。Zhang等[13]提出了基于季冻区3年现场监测温度数据的经验模型，表明路基温度分布主要受地理位置和路基高度影响，横向温差普遍存在。对于养护措施，Liu等[14]研究表明碎石夹层路堤与垂直通风管道相结合可以有效控制多年冻土区地温，提高高速公路路堤稳定性。周亚龙等[15]基于三维有限元分析，预测了输电塔热棒桩基的长期降温效果，并给出了工程建议。Ni等[16]使用沉降指数、风险区带指数和许用承载力指数来评估青藏高原多年冻土区的沉降风险。Duvillard等[17]评估法国阿尔卑斯山永久冻土上基础设施的不稳定风险水平，并讨论利益相关者制定的适应和缓解策略。

现直接从数据角度出发，结合统计推断，通过时间序列模型对青藏铁路路基高程数据进行分析，由Box-Jenkins建模方法确定合适的时间序列模型，并由此进行青藏铁路路基高程至2023年危险点的预测，并由预测结果给出工程建议。

1 青藏铁路路基高程数据预处理

K1425+050处左侧各年月数据为例,如表1所示。

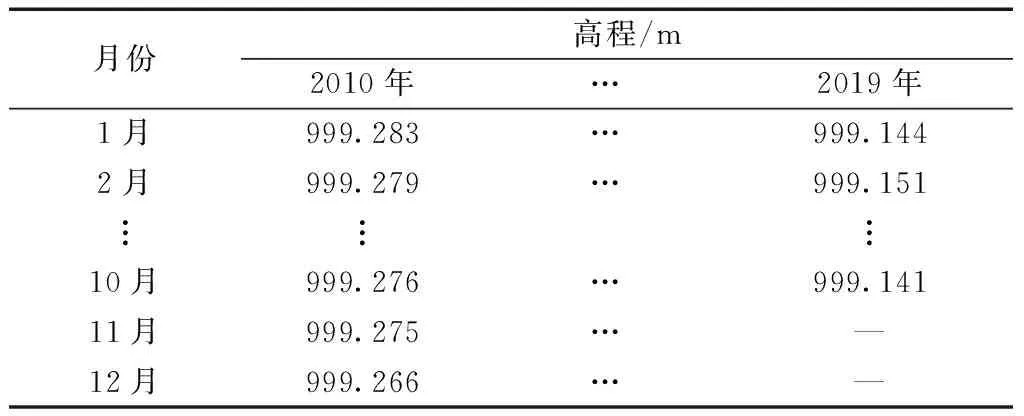
表1 K1425+050处左侧各月路基高程数据

由于青藏铁路路基位处冻土区区段部分受恶劣环境影响，从汇总各年总融沉量的数据来看，各年的路基高程呈下降趋势，因此数据有明显的趋势性，下面通过差分法消除数据趋势性，为下一步模型建立提供基础。

选取差分法去除路基高程数据的趋势性，设时间序列{Yt}的观察序列为{yt,t=1,2,…,N}，则序列的一阶差分即为

∇Yt=Yt-Yt-1=(1-B)Yt

(1)

式(1)中：∇称为差分算子；B为后移算子，即BYt=Yt-1。差分后的数据需经过DF检验(Dickey-Fuller test)确定其是否平稳，即检验γ是否为零。设差分后DF检验模型为

∇Yt=a1+a2t+γYt-1+ut

(2)

式(2)中：a1、a2为外生变量；t为时间；ut为白噪声序列。对差分后数据进行统计特征分析，画出一阶差分直方图，如图1所示。

图1 一阶差分数据直方图Fig.1 Histogram of first-order difference data

经计算可得，一阶差分后，K1425+050处左侧数据平均值为-0.001 233 645，标准差为0.003 780 734，样本偏度为0.878 933 3，样本峰度为7.432 754，样本均值在(0±2) s，即2倍标准差范围内，可以认为一阶差分后的数据为零均值过程，符合Box-Jenkins方法。

2 青藏铁路路基高程数据时间序列模型识别与初步定阶

路基高程一阶差分数据的自相关系数图与偏相关系数图，如图2与图3所示。

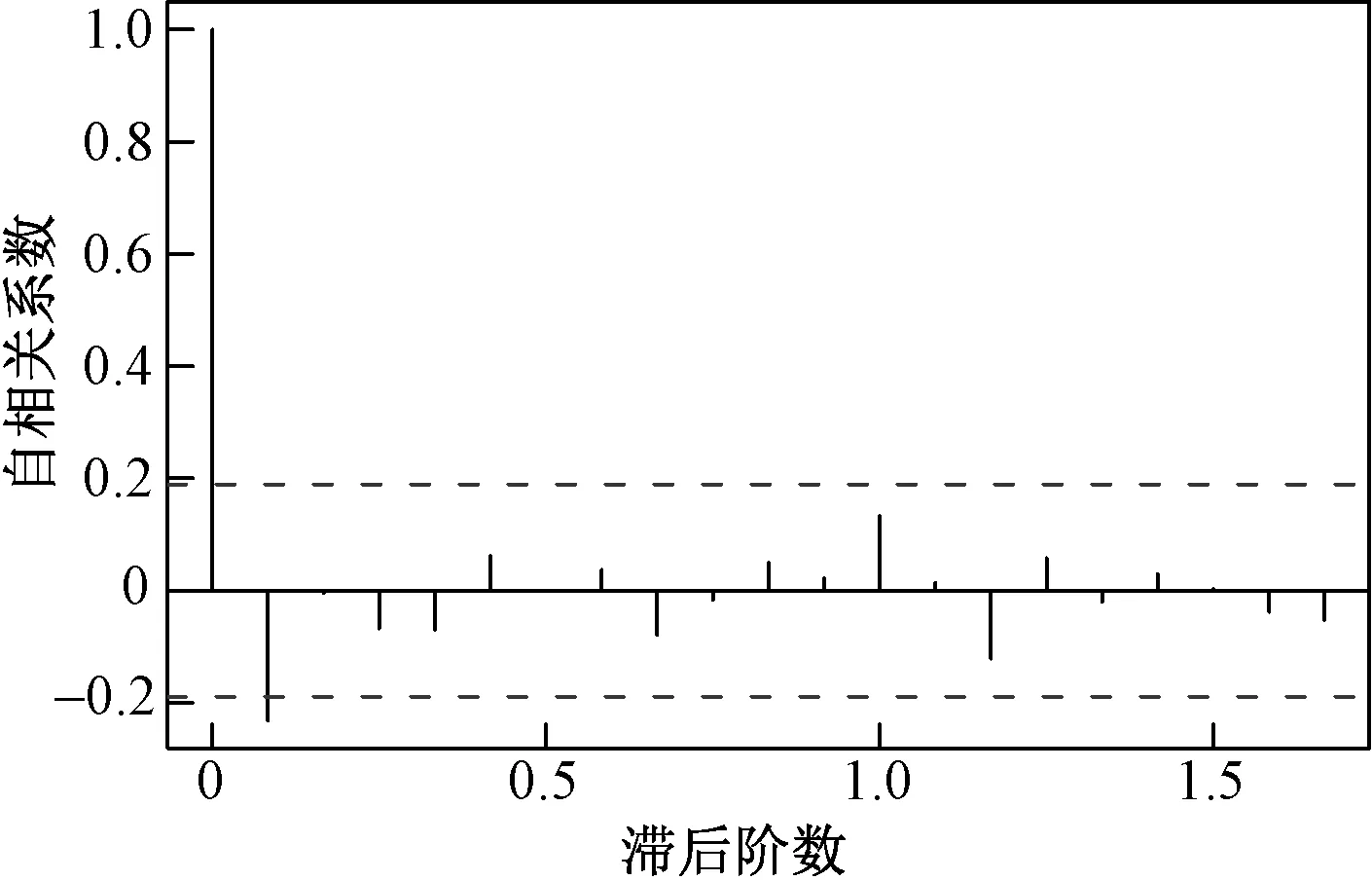
图2 一阶差分自相关系数图Fig.2 The first-order differential autocorrelation coefficient diagram

图3 一阶差分偏相关系数图Fig.3 The first-order differential partial correlation coefficient diagram

(3)

显然有

所以只需检验

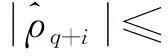
i=1,2,…,M-q

(4)

是否成立，即可判断零均值平稳序列{Xt}的自相关系数是否在q步截尾，是否建立MA模型(moving average model)，其中M是自相关阶数。

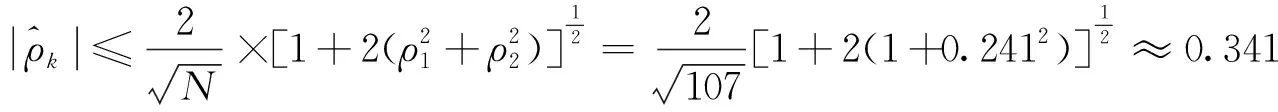
因此，可认为自相关系数2阶截尾，可考虑MA(2)建模。

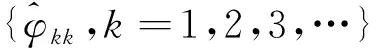
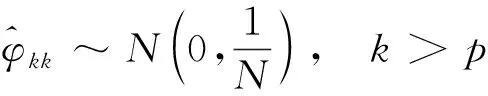
(5)

所以只需检验

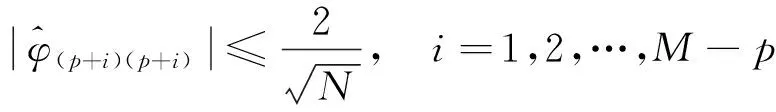
(6)

是否成立，即可判断零均值平稳序列{Xt}自相关系数是否在p步截尾，是否建立AR模型(auto regressive model)，M为偏相关系数。观察图3可知各偏相关系数满足

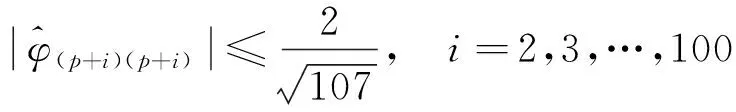
(7)

因此，可选择建立AR(1)模型。

通过Box-Jenkins方法建立进一步的ARMA模型，其特点为初步设定相关模型为ARMA(n,n-1)，即初步设定的相关模型中自回归的阶数比移动平均的阶数高一阶，而选用ARMA(n,n-1)模型来拟合时间序列的原因如下[18]。

(1)AR(p)、MA(q)、ARMA(p,q)模型均为ARMA(n,n-1)模型的特殊情形。

(2)对任一平稳随机系统，均可用ARMA(n,n-1)模型近似。

(3)以差分方程理论可证明，若自回归的阶数是n，则移动平均的阶数是n-1。

(4)从连续系统的离散化过程来看，ARMA(n,n-1)具有合理性。在一个自回归阶数为n阶，移动平均阶数为任意阶的线性微分方程的形式下，如果对一个连续自回归移动平均过程进行一致区间上的抽样，那么，抽样过程的结果是ARMA(n,n-1)。

用Box-Jenkins方法建立模型，即从低阶到高阶对模型进行拟合及检验，若{Xt}属于ARMA模型，则采用ARMA(n,n-1)，并从n=2到高阶对模型逐个进行拟合和检验，根据AIC准则最终确定模型。对选出的模型进行适应性检验，进一步检验模型。

结合上述模型思想，可以尝试建立ARMA(2,1)模型进行拟合。下面对选出的3个模型进行参数的拟合和模型选择。

3 基于AIC准则的模型确定方法

对于平稳序列{Xt,t=0,±1,±2,…}，通过R软件用极大似然估计可算得选出的ARIMA(0,1,1)、ARIMA(1,1,0)、ARIMA(2,1,1)模型参数值，且各模型的AIC值也可计算得到，结果如表2所示。

表2 模型参数估计值与各AIC值

由表2可知，最小AIC值在模型为ARIMA(2,1,1)时取得，因此，确定最终模型为ARIMA(2,1,1)。模型表达为

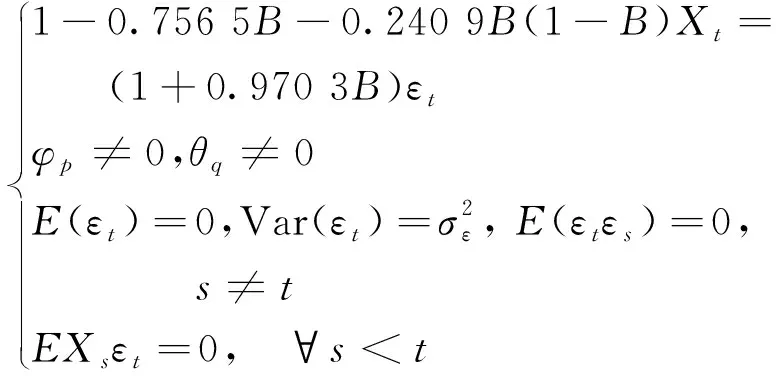
(8)

ARIMA模型是分析和研究时间序列问题的常用方法。该方法能更有效地表征数据序列的线性特性，具有较好的短期预测效果[19]。

4 模型的适应性检验与预测

从残差来看，时间序列模型得到的残差应具有纯随机型，因此，需要判断残差的正态性，通过图4所示残差数据的Q-Q图(quantile-quantile plot)可以看出，残差散点集中于直线附近，因此模型(4)对应的残差具备正态性。

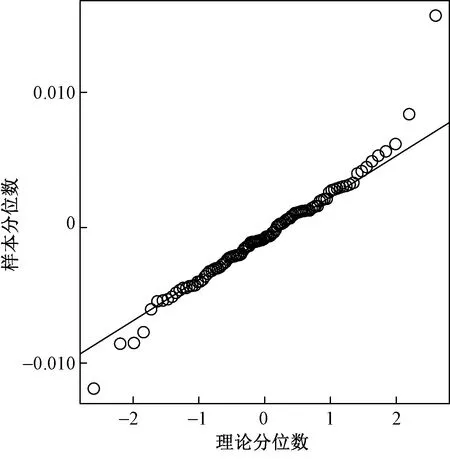
图4 残差数据的Q-Q图Fig.4 Q-Q diagram of residual data

通过自相关系数图与偏相关系数图，如图5、图6所示，与式(2)与式(3)判断，残差序列为纯随机序列。因此，模型(4)具备适应性。因此由该模型进行预测，预测结果如图7所示。

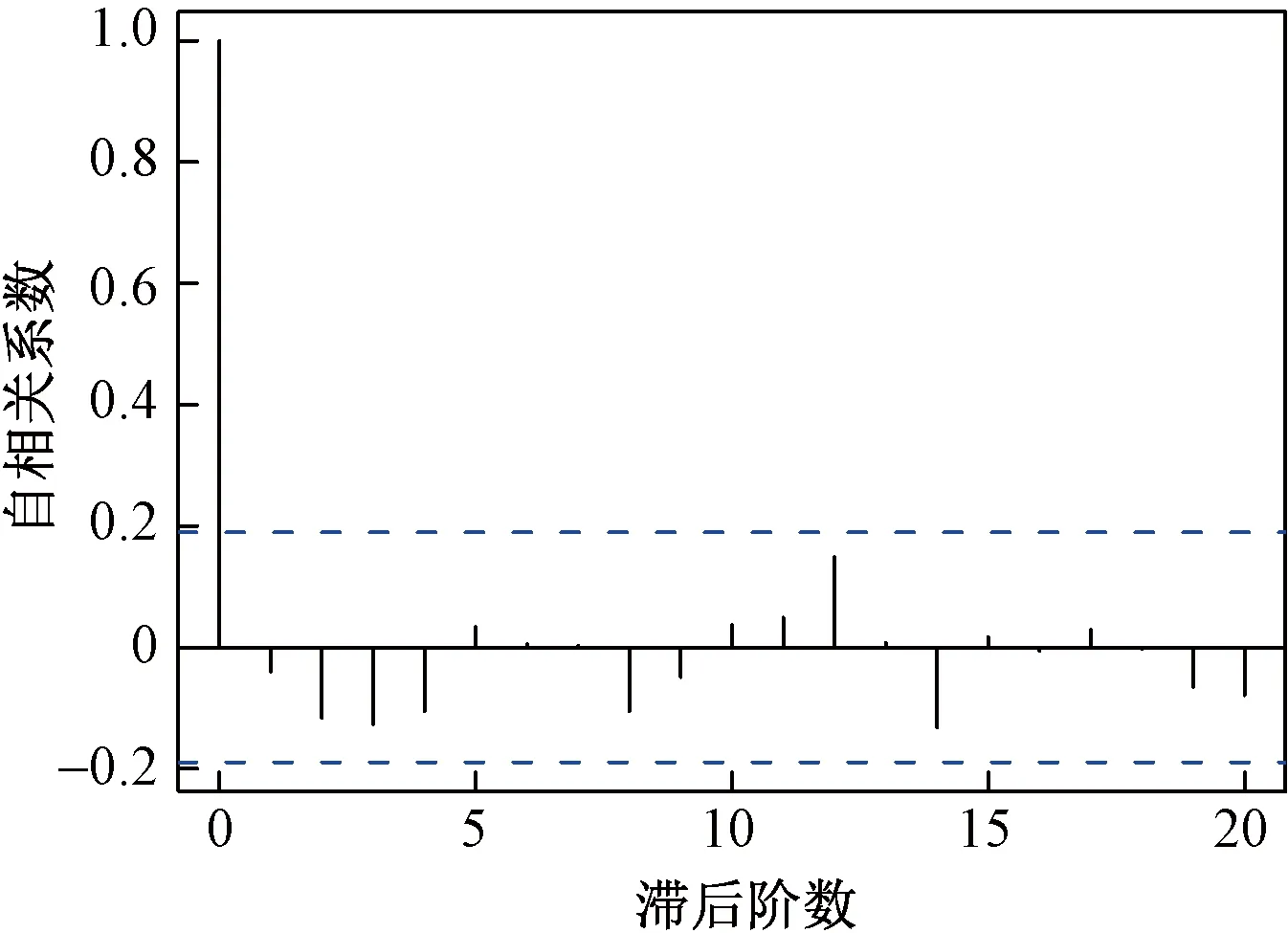
图5 残差自相关系数图Fig.5 Residual autocorrelation coefficient plot

由图7可见，模型对实际数据的拟合较好，而预测数据大致呈现直线状态，这是由于所选测点处，数据线性趋势较为明显。

图7 路基高程预测图Fig.7 Roadbed elevation prediction map

预测数据与测试集数据记录于表3中。

由表3可见，由于数据具有明显的线性性质，预测值呈现直线下降趋势，无法真实地模拟数据的情况，这是由于青藏铁路气候环境复杂，影响其高程变化的因素较多，不会呈现严格的统计性质，且从预测绝对值来看，预测值没有呈现偏差越来越大的趋势，因此，预测结果具备可信度。

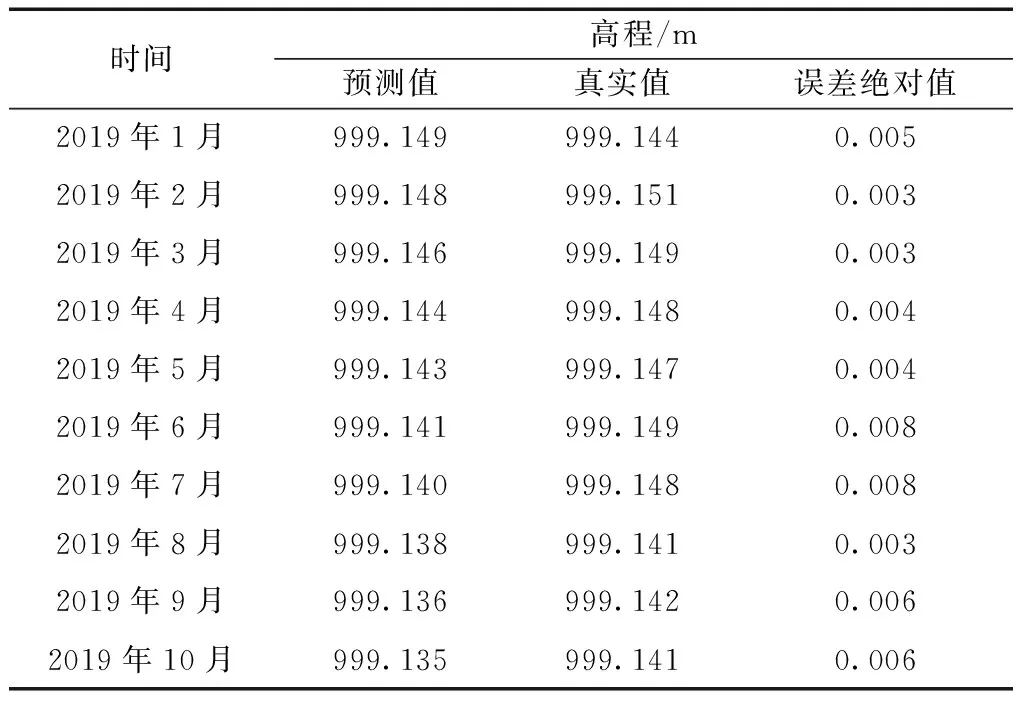
表3 路基高程预测值与真实值比较

按照以上建模步骤建立全部测点的融沉值的时间序列模型，并进行预测，具体步骤如下。

Step 1由于路基融沉值在不同测点处的数据总是呈现一定趋势性的，因此默认进行一阶差分来消除数据趋势性。

Step 2当差分后数据仍不是平稳数据时，为判断数据是否具有周期性，从3阶差分逐步进行到12阶差分，每次差分后判断序列是否平稳，以此找出序列周期性。

Step 3找到序列周期性后，对数据进行去除周期性以使数据平稳，对平稳化后的数据进行模型定阶，并以此模型进行路基高程数据的预测。

结合上述步骤得到各路基测点处路基高程至2023年12月预测值，根据其沉降量与路基左右侧差值，总结了各预测中可能出现重大变形的危险点如表4所示，在预测期内，测点左右两侧路基高程差值出现较大差值的测点，如表4所示。为工程维护等提供参考。

表4中为各测点路基变形值，路基左右侧差值在预测期内前十的测点，由两侧差值较大的测点中可见，集中于K1476+550、K1476+650、K1476+600路基的左右两侧出现明显长距离的差异，因此，在K1476+600地点附近路基需要得到重点维护。

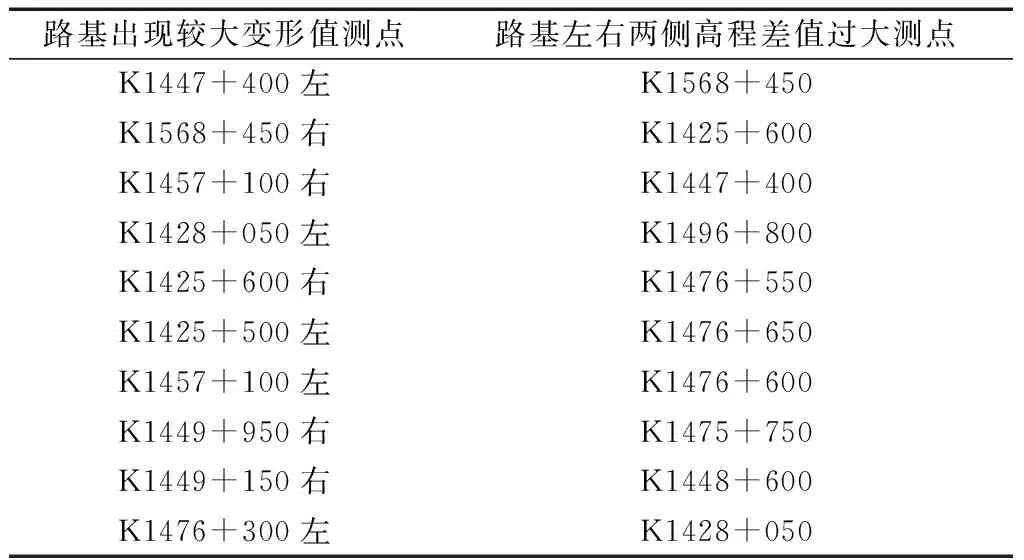
表4 预测期出现危险变形测点

5 结论

青藏高原独特的地理环境导致多年冻土区沿线的路基都不同程度地出现了冻胀、融沉等地质灾害，所以研究多年冻土区路基沉降变形十分有必要。以青藏铁路多年冻土区路基变形的数据为研究对象，得到如下结果。

(1)Box-Jenkins建模方法确定合适的时间序列模型为ARIMA(2,1,1)，通过了模型适应性检验，模型对实际数据拟合较好，预测结果具备可信度。

(2)总结了预测中可能出现重大变形的10个危险点，在预测期内，测点左右两侧路基高程差值出现较大差值的10个测点，为工程维护等提供参考。

(3)测点K1476+600附近，路基的左右两侧出现明显长距离的差异，该地点需要得到重点维护。

研究结果可为工程设计、施工和维护提供有价值的参考，并为青藏高原多年冻土融化沉降危害的预警和预防提供参考。但针对长期预测效果精度的研究，还需进一步扩展。