基于实际竖向荷载分布的波纹钢板剪力墙轴压屈曲分析

赵秋红，高俊秀，邱 静

基于实际竖向荷载分布的波纹钢板剪力墙轴压屈曲分析

赵秋红1, 2，高俊秀1，邱 静1

(1. 天津大学建筑工程学院，天津 300350；2. 滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300350)

波纹钢板剪力墙是一种采用波纹钢板作为内嵌墙板的新型钢板剪力墙结构，具有较高的强度、延性及耗能能力，可作为多层及高层建筑的抗侧力结构体系．内嵌波纹墙板可与边框同步安装，不可避免地会承受上部楼面及边框柱传递的竖向荷载，因此，对波纹钢板剪力墙在竖向荷载作用下的轴压稳定性及屈曲承载力进行研究具有重要意义．将波纹墙板简化为正交各向异性平板，利用微分方程幂级数求解法，推导了线性、非线性分布的轴压荷载作用下波纹墙板弹性屈曲承载力的理论分析方法，并结合三维精细有限元分析结果对该理论分析方法进行修正，以弥补波纹墙板简化产生的误差．建立了多层波纹钢板剪力墙结构的精细有限元模型，并对竖向荷载在各层墙板的分布规律进行研究，发现顶层墙板中竖向应力沿跨度方向呈抛物线分布，并得到了竖向荷载的分布函数，其余楼层墙板中竖向应力近似均匀分布．根据实际竖向荷载分布，提出了波纹钢板剪力墙结构中墙板轴压屈曲荷载的显性计算公式，并通过精细有限元分析验证了该计算公式的有效性．由参数分析结果可知，在其他几何参数不变的情况下，波纹墙板轴压屈曲应力随直边长度的增加显著降低，随平区格板宽度、波折角和区格板宽度比的增加而增加，而波纹边长度和板厚的影响不大．

波纹钢板剪力墙；轴压屈曲荷载；实际竖向荷载分布；正交各向异性板；幂级数求解

波纹钢板剪力墙是一种采用波纹热轧钢板为内嵌墙板的新型钢板剪力墙结构，由于其具有较高的强度、延性及耗能能力，可作为多层及高层建筑的抗侧力体系[1-5]．相较于平板而言，波纹板的屈曲强度显著提高，可有效解决传统平墙板在竖向荷载作用下易屈曲而需滞后安装的问题，从而显著提高建筑尤其是高层建筑的施工效率[2]．但是，由于内嵌墙板与边框同步安装，波纹墙板不可避免地会承受上部楼面及边框柱传递的竖向荷载，呈现压剪联合受力的特征，其抗侧承载力亦将受到竖向应力的影响[6-7]，因此，对波纹钢板剪力墙在竖向荷载作用下的轴压稳定性及屈曲承载力进行研究具有重要意义．

波纹板在轴压荷载作用下可能出现整体屈曲或局部屈曲两种屈曲模态，其中局部屈曲荷载主要由区格板自身柔度决定，可采用经典薄板理论计算[8]，因此本文不再赘述．目前，针对波纹板轴压整体屈曲的研究极为有限．李靓姣[9]通过有限元进行了四边简支正弦波纹板在均布轴压荷载作用下的弹性屈曲分析及参数分析，并拟合有限元数据提出了波纹板的轴压整体屈曲荷载计算公式．

在钢板剪力墙中，竖向荷载由上部楼面及边框柱传递到墙板中，并非一定为均匀分布．针对平钢板剪力墙的研究表明，竖向荷载在墙板中沿宽度方向呈非均匀分布[10]，其中靠近边框柱的区域高、中部区域低，而竖向荷载在波纹钢板剪力墙中的传递和分布规律尚待研究．另一方面，针对板在非均布轴压荷载作用下的屈曲稳定性的研究目前均集中于矩形平板，其中Kang等[11]研究了线性分布轴压荷载作用下的两对边简支板的屈曲，Jana等[12-13]研究了集中荷载和正弦分布轴压荷载作用下的四边简支板的屈曲，而Wang等[14-15]研究了余弦分布轴压荷载作用下的矩形板屈曲．

本文在正交各向异性薄板理论的基础上，利用微分方程幂级数求解法[16]，推导了任意分布形式轴压荷载作用下的波纹钢板弹性整体屈曲荷载的理论分析方法，并通过与精细有限元分析结果的对比，验证了该方法的准确性．通过与波纹墙板精细有限元分析结果的对比，对该方法提出修正以弥补波纹板简化产生的误差．建立波纹钢板剪力墙结构的精细有限元模型，对竖向荷载在各层墙板的分布规律进行研究，根据实际竖向荷载分布提出了波纹墙板的轴压屈曲荷载简化计算公式．

1 竖向荷载作用下波纹墙板竖向应力分布

1.1 多层波纹钢板剪力墙竖向应力分布

采用波纹钢板剪力墙的多层框架结构如图1所示．为探究竖向荷载在多层波纹钢板剪力墙结构中的传递和分布规律，利用有限元软件ABAQUS建立了5层波纹钢板剪力墙的精细有限元模型，如图2所示．为便于论述，本文中波纹墙板的几何尺寸用“”表示，其中分别为墙板的高度、跨度、厚度、平区格板宽度，单位均为mm；为平、斜区格板宽度比；为波折角，单位为(°)；如图3所示.

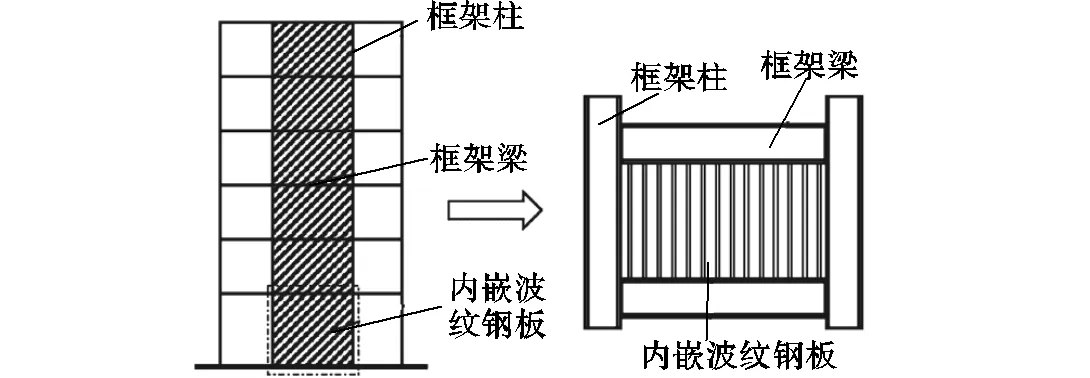
图1 采用波纹钢板剪力墙的典型多层框架结构

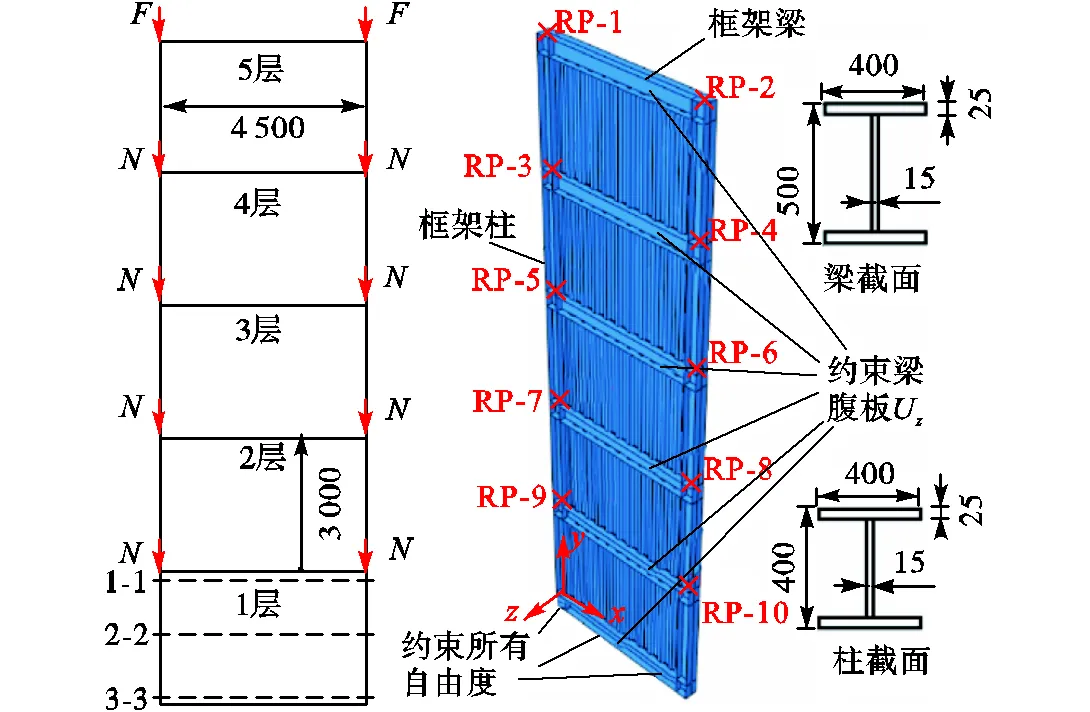
图2 5层波纹钢板剪力墙模型

模型波纹墙板的尺寸为3000-4500-10-120-1-45，边框梁、柱截面尺寸分别为500×400×15×25和400×400×15×25，单位均为mm，如图2所示.梁上楼面传递的均布竖向荷载值为20kN/m，边框柱传递的集中竖向荷载值和分别为5000kN(包含上部楼层产生的竖向荷载[17])和800kN.内嵌波纹钢板及框架梁柱构件均采用S4R壳单元模拟，钢材采用理想弹塑性本构模型，弹性模量为206GPa，泊松比为0.3，墙板和梁柱构件屈服强度分别为235MPa和345MPa．框架梁柱刚接，约束各层梁腹板面外位移以模拟楼板的约束作用，约束底层梁下翼缘所有自由度以模拟刚接基础，在各层柱形心处设参考点并耦合柱截面．

图3 波纹钢板参数

在各层梁上翼缘施加竖向均布荷载，在各层柱形心参考点上施加竖向集中荷载，进行静力分析所得各层墙板中竖向应力沿墙板跨度的分布曲线如图4所示．由图可见，顶层波纹墙板的竖向应力沿跨度方向呈抛物线分布，而其余层墙板的竖向应力沿跨度方向几乎呈均匀分布．这主要是由于中间楼层梁与波纹墙板上下相连，其抗弯刚度显著提高，在竖向荷载作用下，墙板与边框柱共同变形，因此竖向应力的分布趋于均匀，而顶层梁仅下侧与波纹墙板相连，梁的挠曲变形导致顶层波纹墙板竖向应力分布不均匀，靠近边框柱时应力逐渐增大．

图4 波纹钢板墙竖向应力分布

1.2 顶层墙板竖向应力参数分析及分布函数

由于多层波纹钢板剪力墙的顶层与单层波纹钢板剪力墙相似，建立了37个单层波纹钢板剪力墙的有限元精细模型，模型具体参数见表1．

对顶层墙板的竖向应力分布模式进行参数分析，分别考虑了墙板高度、跨度、厚度、局部波形尺寸以及梁、柱刚度等参数的影响．波纹墙板竖向应力分布随各参数的变化规律如图5所示，其中多参数同时变化的模型(M-33～M-37)数据曲线对板内竖向应力及沿板宽距离均进行了归一化处理，分别除以板边竖向应力值0及墙板宽度．由图可知，竖向应力均基本呈抛物线型分布，框架梁刚度、墙板跨度、墙板高度、墙板厚度以及波幅对竖向应力分布均有一定影响，但区格板宽度比和波长的变化对竖向应力分布几乎无影响．框架柱刚度虽会影响竖向应力的大小，但对其分布模式影响很小．

根据有限元分析结果拟合得到顶层墙板竖向应力分布函数如式(1)所示．根据式(1)计算所得竖向应力分布亦绘制于图5，由图可知，在跨高比为0.5～2.0、高厚比为200～1000、波折角度为25°～65°的范围内，该公式均具有较好的精确性．

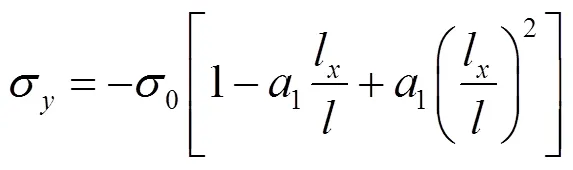
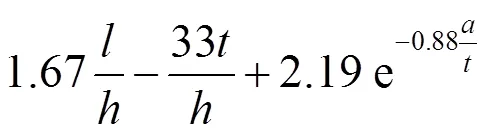
式中：为竖向应力值；l为距墙板左侧边缘的距离；0为墙板边缘处的竖向应力值；e为自然底数；D为波纹板强轴(图3中轴)方向上的单位长度抗弯刚度；为弹性模量；beam为边框梁截面的强轴惯性矩；为墙板的波幅．因此，在竖向荷载作用下，多层波纹钢板剪力墙结构墙板的竖向应力主要有两种分布模式：当框架梁上下两侧均与墙板相连时，竖向应力基本沿墙板跨度均匀分布；当框架梁仅下侧与墙板相连时(顶层墙板)，竖向应力沿墙板跨度呈抛物线形分布，分布函数如式(1)所示．

表1 模型参数

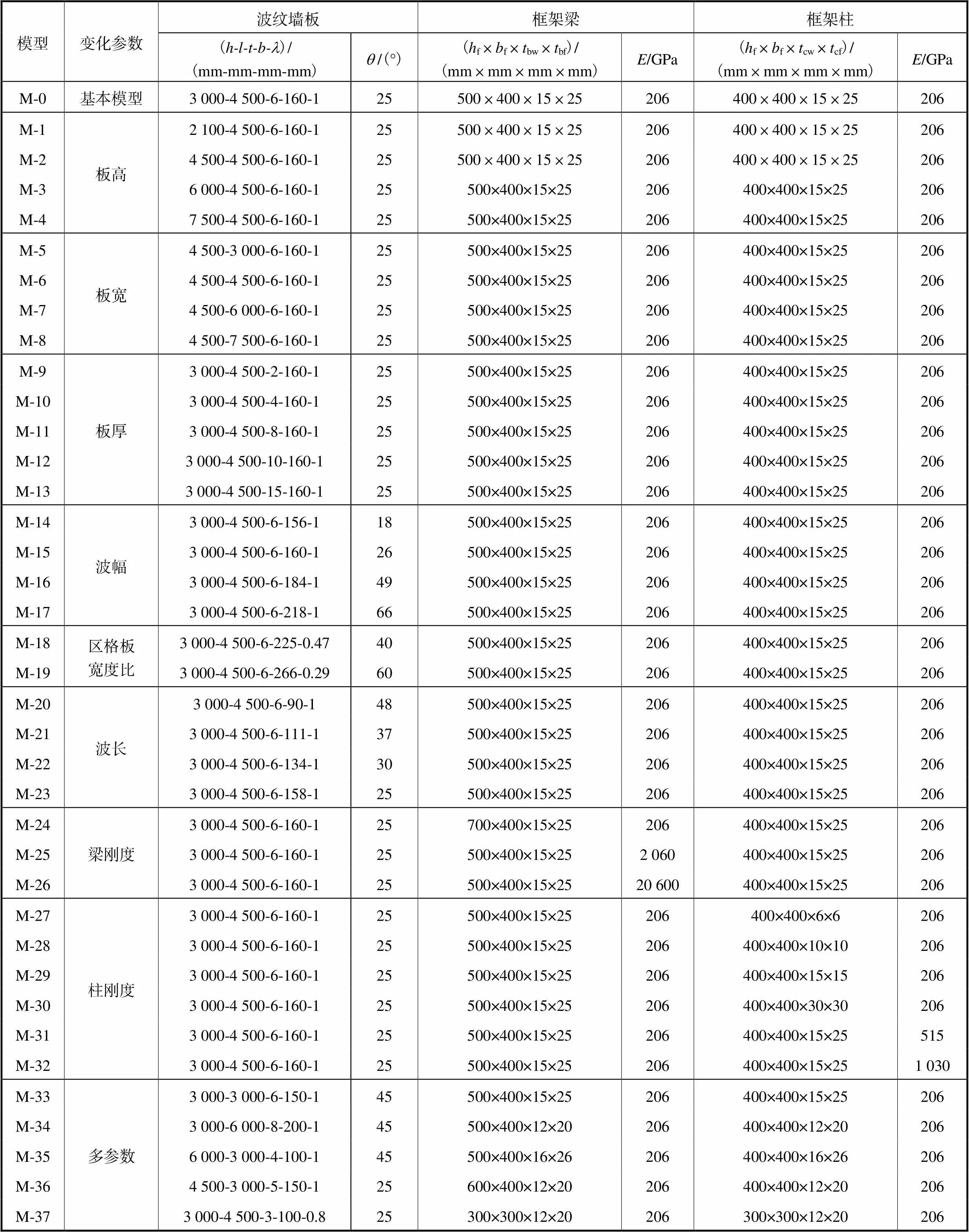
Tab.1 Model parameters

2 轴压屈曲理论分析

2.1 理论推导

将波纹板简化为厚度相同的正交各向异性平板，在正交各向异性薄板理论的基础上，利用微分方程幂级数求解法，推导任意分布形式的轴压屈曲荷载．波纹钢板的计算模型如图6所示．在对边单轴受压作用下，板的屈曲控制微分方程为

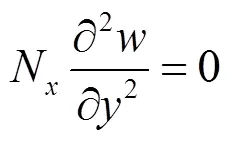
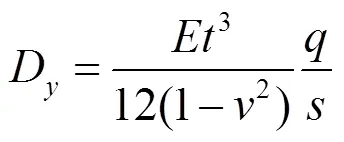
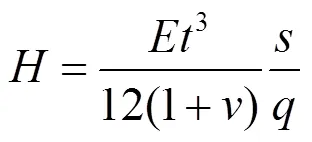
式中：N为作用在波纹边上的单位法向力；为板平面外位移；D为波纹板强轴方向的单位长度抗弯刚度；D为波纹板弱轴方向的单位长度抗弯刚度；为波纹板扭转刚度常数；I为单个波纹截面沿强轴方向的截面惯性矩；为泊松比；其他参数见图3．

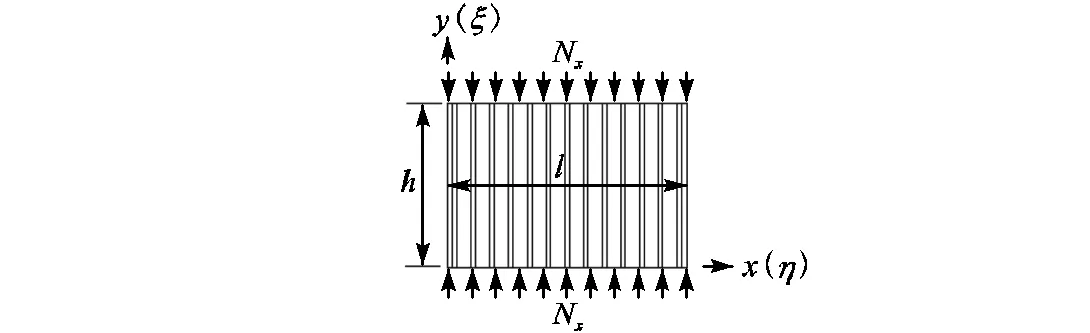
图6 波纹钢板计算模型示意

定义无量纲参数、，

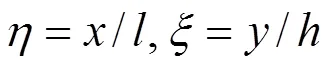
基于Levy方法，考虑到板的两个加载边为简支，采用如式(9)所示的单三角位移函数[18]，其中X为的函数，为板方向上的屈曲半波数．

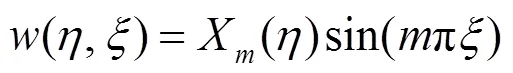
为综合考虑不同的荷载分布模式，选用二次多项式来表示轴压荷载的分布函数N，即

式中：012为常数，不同取值可代表不同的荷载分布模式；0为板边缘处分布荷载．

将式(10)和式(9)代入式(3)中，可得

定义、为

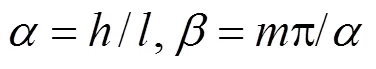
式(11)为常微分方程，仅有一个变系数，可用Frobenius的幂级数解法精确求解，因此，假设变形函数X如式(13)所示，其中C,为待定系数．

利用恒等式性质，任意C可以通过C,0、C,1、C,2和C,3逆推得到．而C,0、C,1、C,2和C,3与非加载边(＝0，1)的边界条件有关，可得到4个具有未知量C,0、C,1、C,2和C,3的齐次方程．分别考虑非加载边为简支和固支两种边界条件进行推导．

非加载边简支：

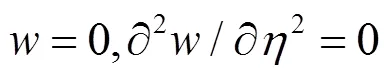
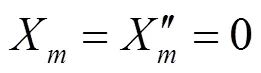
非加载边固支：

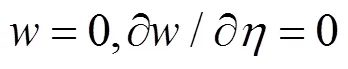
为得到系统的非平凡解，令齐次方程组中系数矩阵行列式为零．通过求解特征值方程，可得到每个纵向屈曲半波数()的无穷多组特征值(无量纲屈曲荷载，0)，所有这些0中的最小值为无量纲临界屈曲载荷0cr．

式(13)给出的精确解函数需要求解无穷级数的和．根据数值计算中的精度等级，求和的上限是一个有限数()，可以根据需要任意大．这一过程与其他边界精确解中超越函数的求解过程没有区别，特征值方程的求解利用MATLAB计算．

2.2 收敛性分析

为了检验式(13)幂级数收敛速度，对图7所示的5种荷载分布形式，考虑四边简支(SSSS)以及加载边简支、非加载边固支(SSCC)两种边界条件进行收敛性分析．表2为各荷载分布形式对应的参数取值．其中N-1为均布荷载，N-2和N-3为线性分布荷载，N-4和N-5为非线性分布荷载．表3为不同荷载分布下特征值求解收敛结果，由表3可知，均匀分布的函数在＝30时达到精确解，线性分布函数在＝50时完全收敛，非线性分布函数＝60时收敛，可见求解非线性分布荷载下的屈曲荷载最复杂．

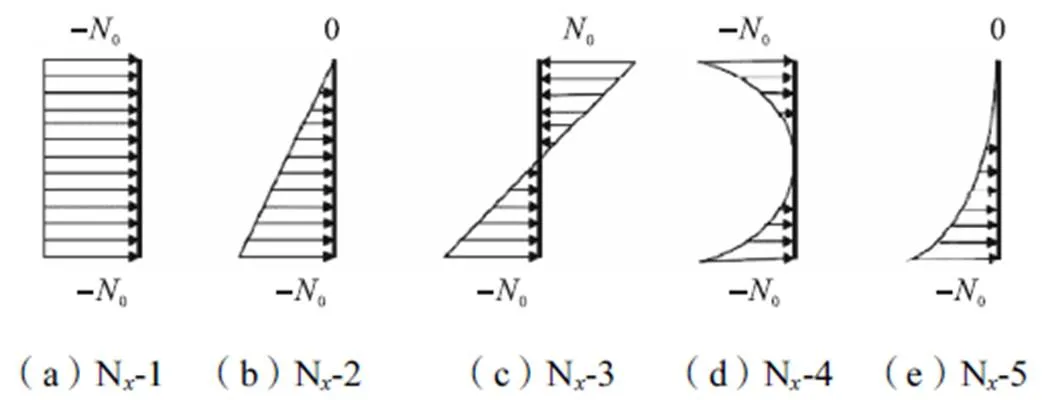
图7 竖向荷载分布形式

表2 竖向荷载分布系数

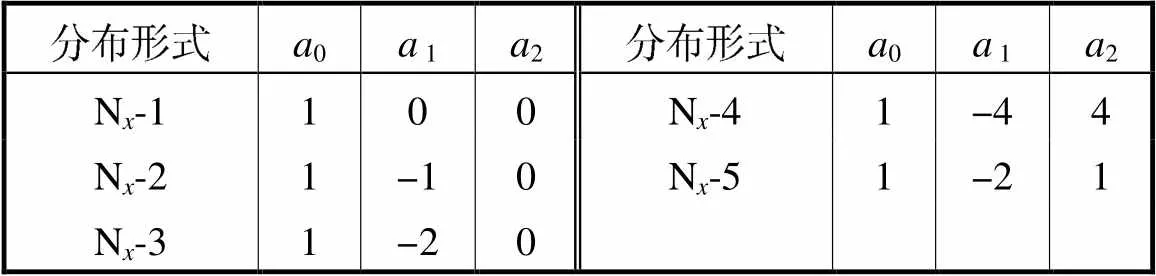
Tab.2 Vertical load distribution coefficient

表3 幂级数收敛性结果

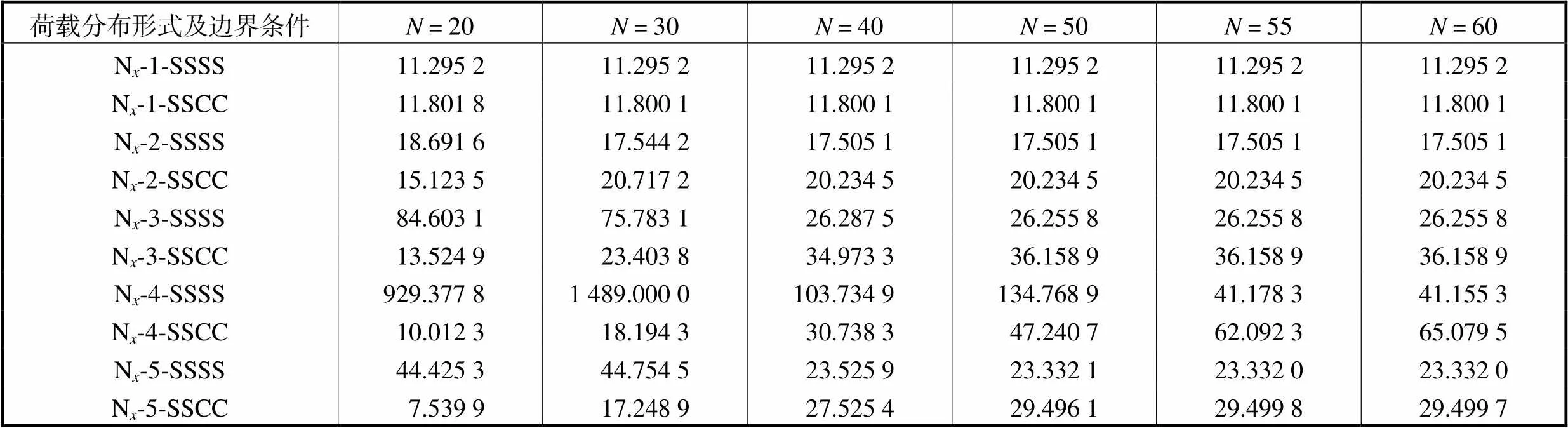
Tab.3 Convergence results of power series

3 轴压屈曲有限元分析

3.1 有限元建模及验证

采用ABAQUS建立三维波纹墙板的精细有限元模型，进行轴压荷载作用下的弹性屈曲分析，模型加载方式及边界条件如图8所示．采用S4R壳单元模拟墙板，钢材弹性模量为206GPa，泊松比为0.3．首先建立了20个不同高厚比(125～875)和长宽比(0.2～5.0)的平板模型进行弹性屈曲分析，所得轴压屈曲荷载与经典薄板理论计算结果对比如图9所示，图中有限元分析和理论计算结果相对误差均小于2%，验证了有限元模型的正确性．在轴压荷载作用下，波纹墙板可能出现整体屈曲模态或局部屈曲模态，而其局部屈曲承载力主要由区格板自身柔度所决定，可采用经典薄板理论计算．因此，本文仅讨论了最低阶屈曲模态为整体屈曲的波纹墙板模型数据．

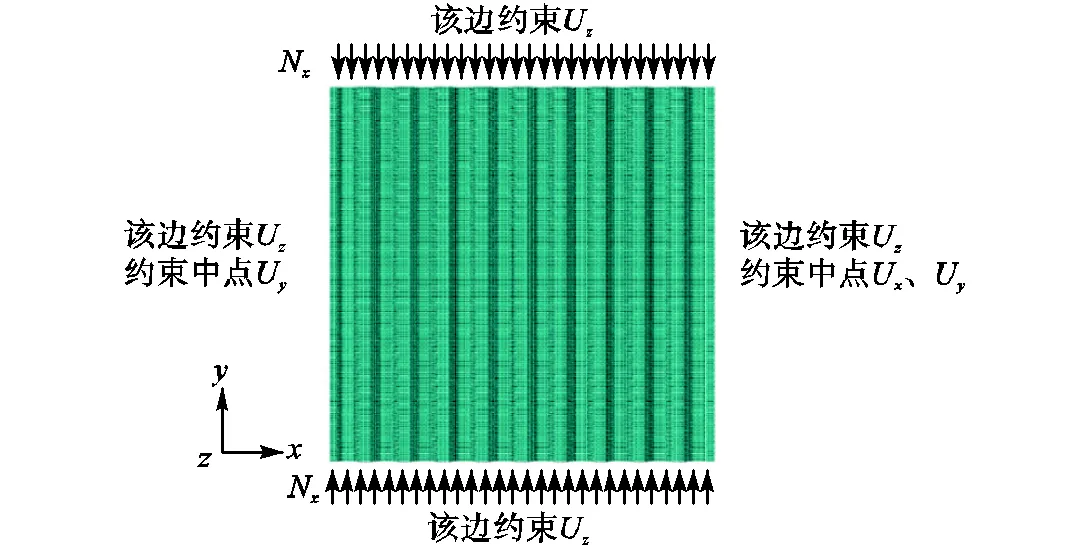
图8 波纹板四边简支模型

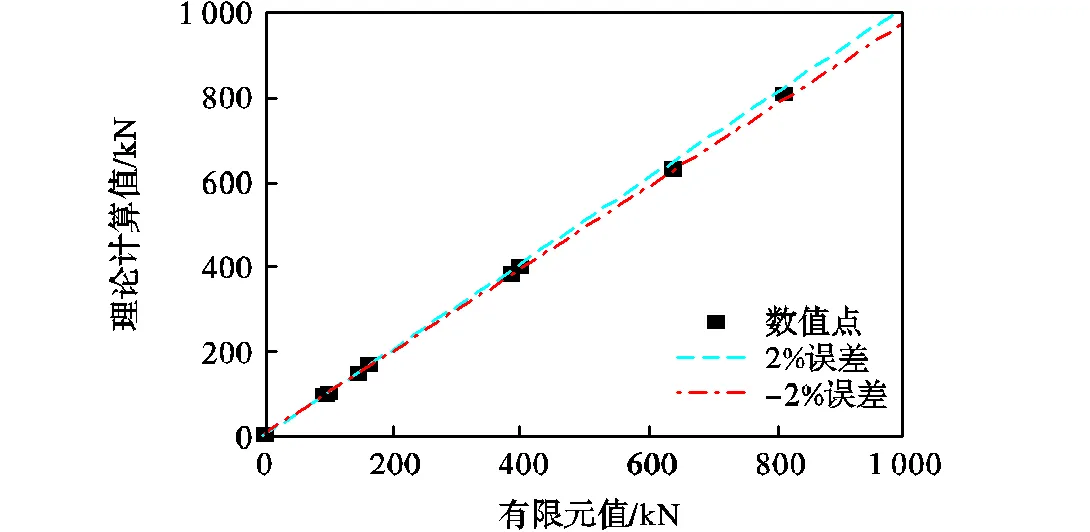
图9 平板模型计算结果

3.2 有限元分析结果

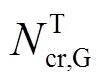
图10 正交异性平板和波纹板屈曲模态

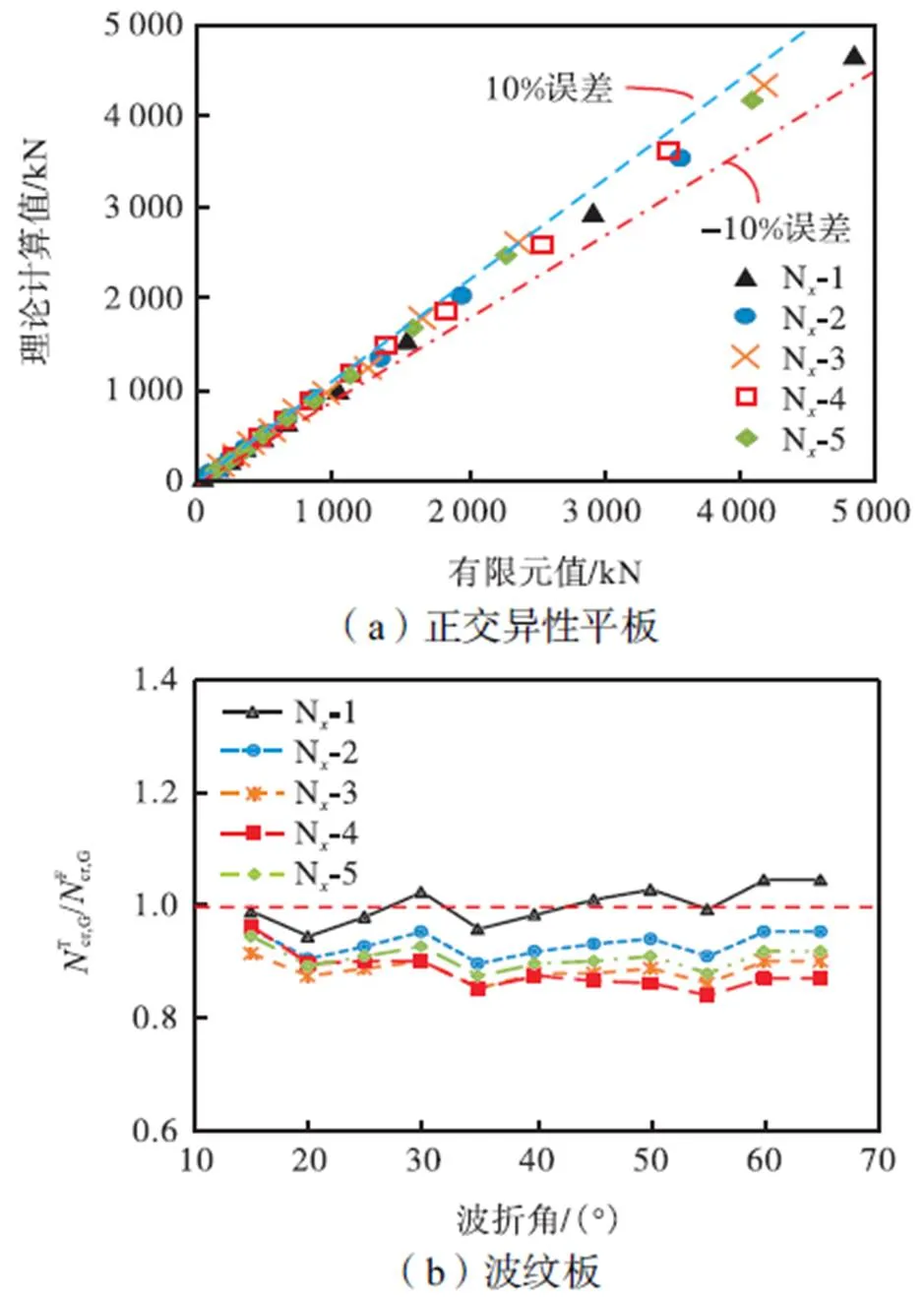
图11 理论分析与有限元分析结果对比

3.3 波纹板理论分析方法修正

定义修正系数为

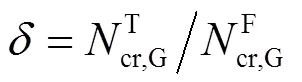
对一系列波纹板分别进行轴压荷载作用下的有限元弹性屈曲分析和理论分析，通过结果对比分析荷载分布模式对修正系数的影响

根据有限元分析结果，提出修正系数计算式为

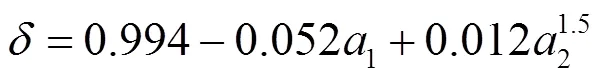
式中荷载分布系数1和2的值见表2．

4 波纹板弹性轴压屈曲的简化计算公式

本文所提理论分析方法为隐式求解方法，计算过程需要借助MATLAB程序，虽计算精度可以得到保证，但过程较为复杂．考虑到竖向荷载作用下，多层波纹钢板剪力墙结构中墙板竖向应力除顶层外多呈均匀分布，一般楼层的波纹墙板轴压屈曲荷载也可采用正交各向异性平板在均布荷载作用下的轴压屈曲荷载式(21)[19]进行简化计算，其中G为弹性屈曲系数，通过隐式计算结果拟合所得．

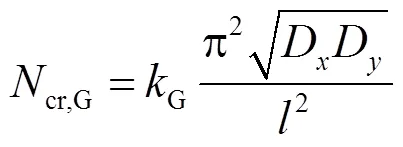
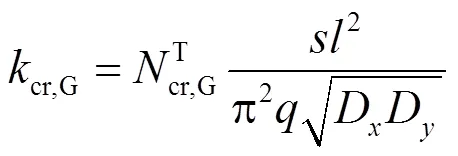
D和D分别按式(4)和式(5)进行计算．

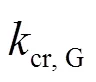
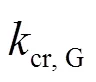
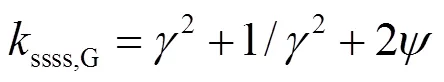
(26)

为了进一步验证该简化计算方法的有效性，且扩大参数变化范围，满足实际应用的需要，对1200个不同几何尺寸的波纹墙板有限元精细模型进行了弹性轴压屈曲分析，所考虑的参数变化包括板高(2.1～7.5m)、板宽(2～7.5m)、板厚(2～30mm)、区格板宽(50～200mm)、波幅(10～100mm)、波长(200～600mm)及非均匀荷载分布模式．由图13可知，公式计算与有限元分析结果吻合良好，其相对误差的平均值为2.17%，标准差为1.6%，1200个数据中约97%的数据误差在6%以内，可见，所提出的简化计算方法可为波纹墙板的整体轴压屈曲荷载提供合理准确的预测结果．

图13 四边简支波纹板弹性整体轴压屈曲应力值的相对误差分布

考虑到计算公式的复杂性，为了更直观地反映各几何参数对波纹板整体轴压屈曲应力的影响，便于设计参考，图14给出了整体轴压屈曲应力的有限元分析和计算结果随各几何参数的变化，包括波纹边长、直边长、板厚、平区格板宽度、区格板宽度比和波折角．图14中公式计算结果由式(27)计算得到．结果表明：计算结果能很好地反映各几何参数的影响，在其他几何参数不变的情况下，波纹边长和板厚的变化对波纹板的整体轴压屈曲应力影响不大，而直边长的增加则使整体轴压屈曲应力显著降低；板厚、平区格板宽度、波折角和区格板宽度比均与整体轴压屈曲应力呈正相关；通过改变波纹参数来提高整体轴压屈曲应力比增加板厚更为有效．

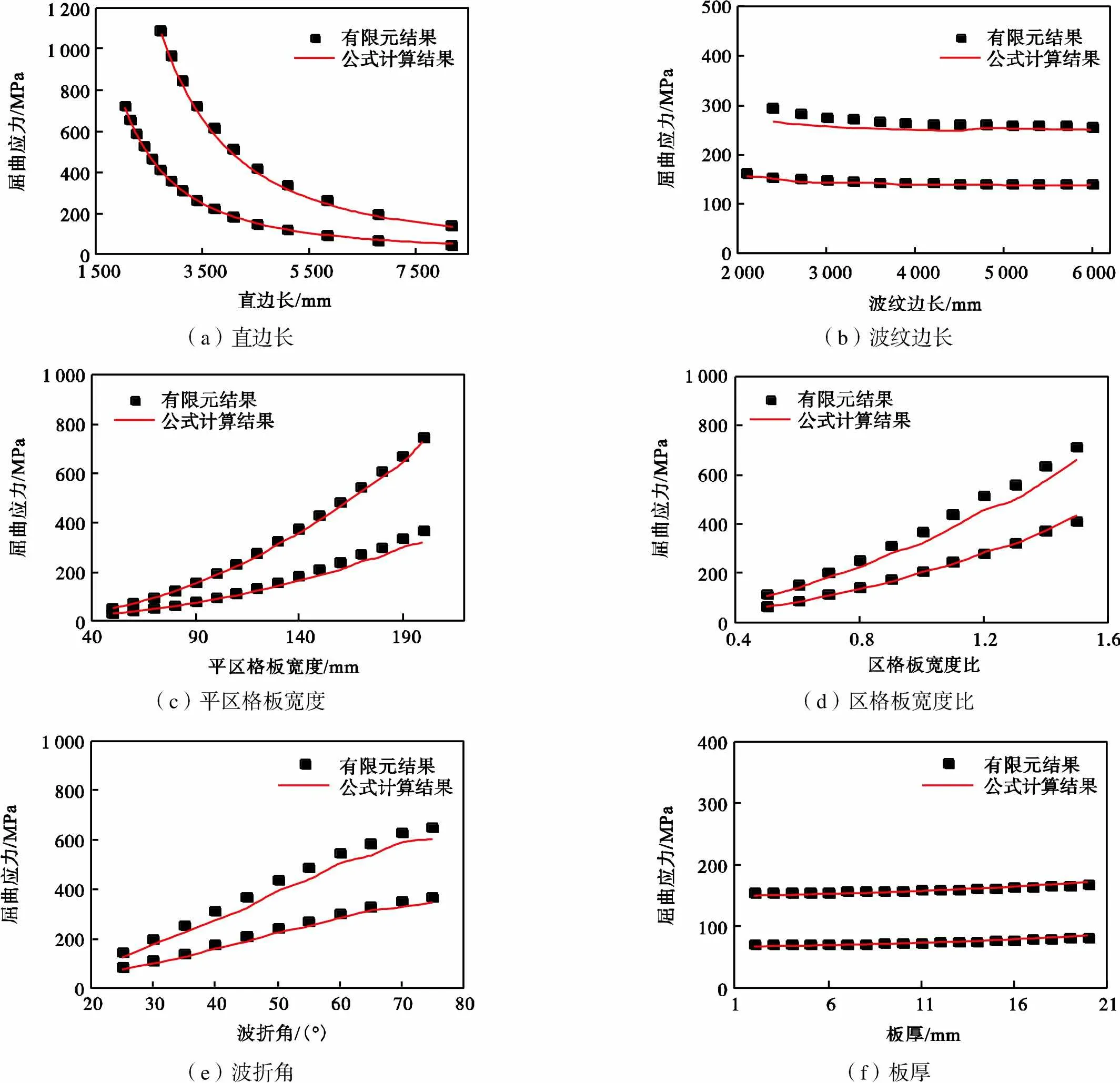
（a）直边长（b）波纹边长 （c）平区格板宽度（d）区格板宽度比 （e）波折角（f）板厚

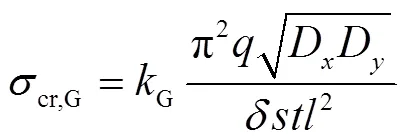
图15进一步给出了轴压屈曲应力随墙板波折程度的变化．从图15(a)可以看出，在波纹数量不变的情况下，增加波幅可以有效地提高波纹板的整体轴压屈曲应力．但是需要注意的是，增加波幅会同时增加区格板宽度，从而降低局部屈曲应力，所以并非波幅越大越好．由图15(b)可知，在波幅一定时，整体轴压屈曲应力随波长的变化并不明显，因此，在波纹墙板设计时应合理选择波幅．

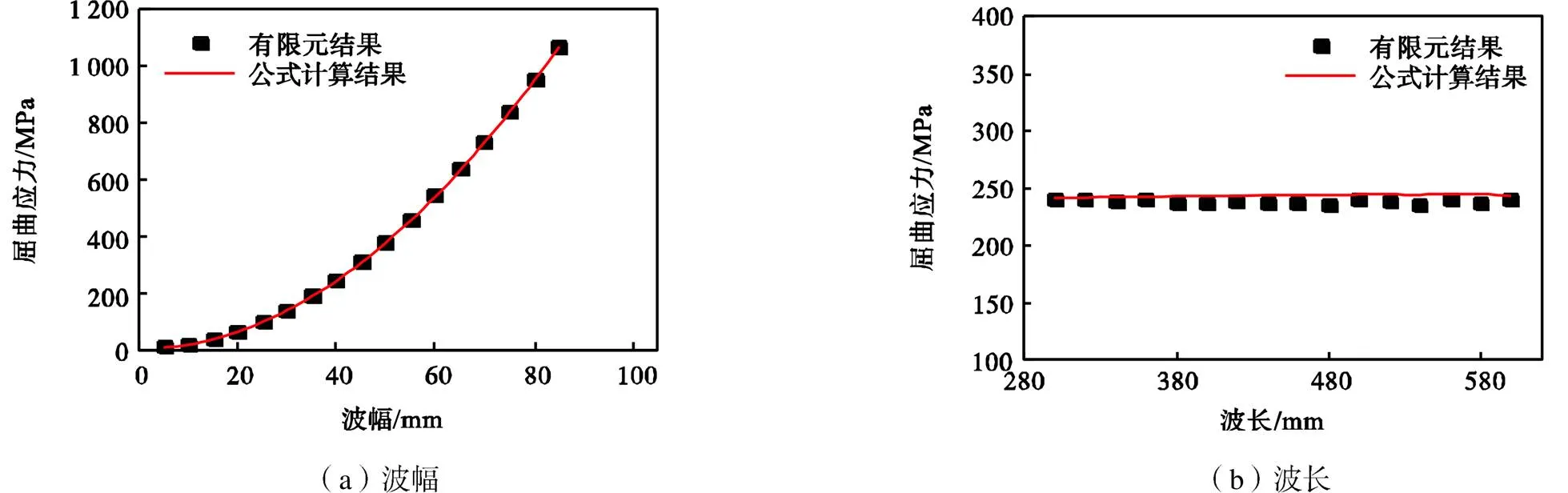
图15 波折程度对波纹板弹性整体轴压屈曲应力的影响

5 结 论

(1) 将波纹墙板简化为正交各向异性平板，利用微分方程幂级数求解法，推导了线性、非线性分布的轴压荷载作用下波纹墙板弹性屈曲承载力的理论分析方法，并结合三维精细有限元分析结果对该理论分析方法进行修正，以弥补波纹墙板简化产生的误差．

(2) 建立了多层波纹钢板剪力墙结构的精细有限元模型，并对竖向荷载在各层墙板的分布规律进行研究，结果表明顶层墙板中竖向应力沿跨度方向呈抛物线分布，其余楼层墙板中竖向应力近似均匀分布，并提出了顶层墙板的竖向荷载分布函数，在跨高比为0.5～2.0、高厚比为200～1000、波折角为25°～65°的范围内，该公式均具有较好的精确性．

(3) 根据实际竖向荷载分布，提出了波纹钢板剪力墙结构中墙板轴压屈曲荷载的显性计算公式，并通过精细有限元分析验证了该计算公式的有效性．

(4) 在其他几何参数不变的情况下，波纹墙板轴压屈曲应力随直边长度的增加显著降低，随平区格板宽度、波折角和区格板宽度比的增加而增加，但波纹边长和板厚对屈曲应力的影响不大．通过改变波形参数来提高波纹墙板整体轴压屈曲应力比单纯增加板厚更为有效．

［1］ Emami F，Mofid M，Vafai A. Experimental study on cyclic behavior of trapezoid ally corrugated steel shear walls[J]. Engineering Structures，2013，48：750-762.

［2］ Qiu Jing，Zhao Qiuhong，Yu Cheng，et al. Experimental studies on cyclic behavior of corrugated steel plate shear walls[J]. Journal of Structural Engineering，2018，144(11)：04018200.

［3］ Cao Q，Huang J. Experimental study and numerical simulation of corrugated steel plate shear walls subjected to cyclic loads[J]. Thin-Walled Structures，2018，127：306-317.

［4］ 赵秋红，李 楠，孙军浩. 波纹钢板剪力墙结构的抗侧性能分析[J]. 天津大学学报(自然科学与工程技术版)，2016，49(增1)：152-160.

Zhao Qiuhong，Li Nan，Sun Junhao. Analysis on lateral performance of sinusoidally corrugated steel plate shear walls[J]. Journal of Tianjin University(Science and Technology)，2016，49(Suppl 1)：152-160(in Chinese).

［5］ 赵秋红，邱 静，郝博超，等. 两边连接竖向波纹钢板剪力墙的抗侧性能[J]. 天津大学学报(自然科学与工程技术版)，2019，52(增2)：46-53.

Zhao Qiuhong，Qiu Jing，Hao Bochao，et al. Lateral behavior of vertically-corrugated steel plate shear walls connected with beams only[J]. Journal of Tianjin University(Science and Technology)，2019，52(Suppl 2)：46-53(in Chinese).

［6］ Nie J，Fan J，Liu X，et al. Comparative study on steel plate shear walls used in a high-rise building[J]. Journal of Structural Engineering，2013，139(1)：85-97.

［7］ Lü Y，Li Z. Influences of the gravity loads on the cyclic performance of unstiffened steel plate shear wall[J]. The Structural Design of Tall and Special Buildings，2016，25(17)：988-1008.

［8］ Timoshenko S P，Gere J M. Theory of Elastic Stability [M]. 2nd ed. New York：McGraw-Hill Publishing Co，1961.

［9］ 李靓姣. 波浪形钢板墙的受力性能及设计方法研究[D]. 北京：清华大学，2012.

Li Liangjiao. Research on Behavior and Design Methods of Sinusoidal Steel Plate Wall[D].Beijing：Tsinghua University，2012(in Chinese).

［10］ Lü Y，Zhao Z，Lü J，et al. Determination of shear strength of steel shear walls with three different vertical stress distributions for considering the gravity load effect[J]. Journal of Constructional Steel Research，2020，170：106-113.

［11］ Kang J，Leissa A W. Exact solutions for the buckling of rectangular plates having linearly varying in-plane loading on two opposite simply supported edges[J]. International Journal of Solids and Structures，2005，42(14)：4220-4238.

［12］ Jana P，Bhaskar K. Analytical solutions for buckling of rectangular plates under non-uniform biaxial compres-sion or uniaxial compression with in-plane lateral restraint[J]. Int J Mech Sci，2007，49：1104-1112.

［13］ Jana P，Bhaskar K. Stability analysis of simply-supported rectangular plates under non uniform uniaxial compression using rigorous and approximate plane stress solutions[J]. Thin-Walled Struct，2006，44：507-516.

［14］ Wang X，Shi X. Differential quadrature buckling analyses of rectangular plates subjected to non-uniform distributed in-plane loadings[J]. Thin-Walled Struct，2006，44：837-843.

［15］ Wang X，Gan L，Zhang Y. Differential quadrature analysis of the buckling of thin rectangular plates with cosine-distributed compressive loads on two opposite sides[J]. Advances in Engineering Software，2008，39(6)：497-504.

［16］ Wylie Jr C R. Advanced Engineering Mathematics[M]. New York：McGraw-Hill，1951.

［17］ Zhang X，Guo Y. Behavior of steel plate shear walls with pre-compression from adjacent frame columns[J]. Thin-Walled Structures，2014，77：17-25.

［18］ 肖明心．板的稳定理论[M]．成都：四川科技出版社，1993．

Xiao Mingxin. Theory of Plate Stability[M].Chengdu：Sichuan Science and Technology Publishing House，1993(in Chinese).

［19］ Hlavacek V. Shear instability of orthotropic panels[J]. Acta Tech CSAV，1968，1：134-158.

［20］ Bergman S，Reissner H. Neue probleme aus der flugzeugstatik[J]. Zeitschrift Flugtech und motor luftsch，1926，17：137-146.

Bergman S，Reissner H. New problems in aircraft statics[J]. Journal of Aviation Tech and Motor Switch，1926，17：137-146(in German).

Axial Compressive Buckling of Corrugated Steel Plate Shear Walls Under Actual Vertical Load Distribution

Zhao Qiuhong1, 2，Gao Junxiu1，Qiu Jing1

(1. School of Civil Engineering，Tianjin University，Tianjin 300350，China； 2. Key Laboratory of Coastal Civil Structure Safety of Ministry of Education(Tianjin University)，Tianjin 300350，China)

Corrugated steel plate shear wall，a new type of steel plate shear wall structure with corrugated steel plates as infill wall plates，could be used as a lateral force-resisting system for mid- to high-rise buildings owing to its high lateral capacity，ductility，and energy dissipation capacity. The corrugated wall plates can be installed synchronously with the boundary frame，which will inevitably bear the vertical load from the upper floor and boundary columns. Therefore，investigating the stability and buckling capacity of corrugated steel plate shear walls under vertical loads is of great significance. In this paper，an analytical method is developed by simplifying as orthotropic plates to determine the elastic buckling capacity of corrugated wall plates under linearly or nonlinearly distributed axial compressive loads，using power series solution to solve differential equations. The analytical method is modified based on three-dimensional finite element analysis to compensate for the errors caused by the simplification of corrugated plates. Finite element models of multistory corrugated steel plate shear walls are established，and the vertical load distribution in the wall plate of each story is studied. It is found that the vertical stress distribution in the wall plate is parabolic in the top-story and approximately uniform in other stories，prompting the development of a vertical stress distribution function for the top-story wall. Based on the actual vertical stress distribution，an explicit formula for calculating the elastic buckling capacity of corrugated wall plates under axial compression is proposed and verified by finite element analyses. Parametric studies show that the elastic buckling capacity of corrugated wall plates under axial compression decreases significantly with an increase in the straight edge length and increases with the increase in flat subpanel width，corrugation angle，and subpanel width ratio，while the length of the corrugated edge and plate thickness have little effect.

corrugated steel plate shear wall；axial compressive buckling load；actual vertical load distribution；orthotropic plate；power series solution

10.11784/tdxbz202104001

TU392. 4

A

0493-2137(2022)04-0391-11

2021-04-01；

2021-05-13.

赵秋红（1975—  ），女，博士，特聘研究员．

赵秋红，qzhao@tju.edu.cn.

国家自然科学基金资助项目(51378340，51678406，51878447).

Supported by the National Natural Science Foundation of China(No. 51378340，No. 51678406，No. 51878447).

(责任编辑：金顺爱)