基于遗传-粒子群优化算法的USV路径规划方法

宫月红，张少君，王明雨，孟雄飞

山东交通学院 航运学院，山东 威海 264209

0 引言

随着国家海洋战略的实施，人们在开发海洋资源的同时，也更加重视对海洋环境的保护与治理。为了及时发现水域污染问题，尽早采取治理措施，应用计算机、通信、电子及自动控制等技术对水域进行监测。采用无人水面舰艇(unmanned surface vessel，USV)对水域环境进行监测，具有无人、智能化、速度快等优势。为保证USV完成对水域的采样巡检任务，根据已知的采样点信息，在USV出发前需要为其规划一条全局路径。采用群智能算法对机器人进行路径规划是目前自动控制领域研究的热点，常用的群智能算法包括蚁群算法、粒子群算法(particle swarm optimization algorithm, PSO)、鱼群算法等[1-3]。智能算法在机器人路径规划领域已有较多可参考的实例[4-10]，对USV路径规划算法的研究尚属前沿领域，可参考方案有限。文献[11]采用改进PSO规划水下航行器路径。文献[12-13]采用改进的PSO对移动机器人进行路径规划，通过动态调整惯性权重实现动态路径调整。文献[14]采用结合PSO改进的遗传算法(genetic algorithm,GA)对USV进行避障路径规划。USV按照一定的顺序访问采样点的过程，可以等效为旅行商问题(travelling salesman problem, TSP)。用于求解TSP问题的路径规划算法包括蚁群算法、PSO、GA等[15-18]，其中PSO在全局路径规划中的应用比较广泛，但存在早熟收敛的问题。

为了提高寻优精度和收敛速度，本文提出一种遗传-粒子群混合算法，在传统PSO的基础上，引入GA中变异、交叉思想，同时按照算法迭代次数对惯性权重进行自适应调整，避免算法陷入局部最优解，提高解的精确性，加快收敛速度。采用Matlab仿真软件，对水域环境地图及采样点分布情况进行建模。分别采用传统PSO及优化后的PSO对USV进行全局路径规划比较，验证路径规划的效果。

1 USV路径规划问题模型

采用USV对一定水域范围内若干个采样点进行自动巡检采样，首先规划USV的行驶路径，目的是在起始点与目的地之间产生一条路径，保证采样点均被巡检到，除起始点外，其余采样点只巡检1次。受限于USV的续航能力，规划的路径总长应尽可能短，这相当于求解TSP问题。假设有N个采样点，可选择的路径为M=N!/(2N)条，如果采用常规的穷举法寻找最短路径，计算量较大，当采样点数目达到一定规模时将难以实现，应选择合适的寻优算法。

TSP问题假设有1个旅行商人要到n个城市，所要走的路径必须经过所有城市，且除了出发城市外，其余城市只访问1次。以规划路径总长为目标，在所有可能的路线中选择1条路径总长最短的路径。定义目标函数为F，n个城市的TSP问题数学模型为

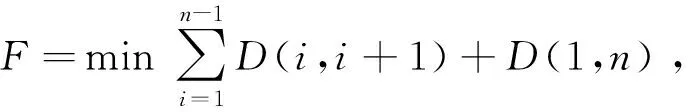
式中D(i，i+1)为城市i到城市i+1间的距离。

若D(i,j) =D(j,i)，i,j∈{1, 2,… ,n}，则称为对称 TSP 问题，否则为不对称TSP问题。本文中USV多点采样问题为对称TSP问题。

2 遗传-粒子群算法

2.1 传统粒子群算法

传统PSO模拟鸟群寻找食物时趋向于靠近离食物最近的同类位置，在每次迭代后都离食物位置更近一些，直到找到食物为止。每只鸟可视作1个粒子，即1个搜索个体。每个粒子都有1个由被优化的函数决定的适应度，每个粒子都有粒子所在位置和粒子速度2个属性。在寻优过程中，每1代粒子所在的位置和搜索速度都发生变化。当寻找空间是1个多维向量时，位置和速度也是多维向量。假设n维空间中有m个个体，第i个个体位置为Xi，速度为vi，公式分别为：

Xi=(Xi1Xi2…Xin)，

vi=(vi1vi2…vin)。

每次迭代需找到粒子自身历史最优位置Ppbest(即局部最优)及群体最优位置Pgbest(即全局最优)，更新速度与位置信息的公式为

vid(t+1)=ωvid(t)+c1R1(Ppbest-Xid)+c2R2(Pgbest-Xid),i=1,2,…，m,d=1,2,…,n，

(1)

Xid(t+1)=Xid(t)+vid(t+1)，i=1,2,…，m,d=1,2,…,n，

(2)

式中：vid(t)为粒子第t代的速度；vid(t+1)为粒子第t+1代的速度；ω为惯性权重，决定算法的搜索速度；c1、c2为参数，分别决定粒子向自身最优和种群最优靠近的速度；R1、R2为随机数，R1、R2∈[0，1]。

本文中适应度对应USV巡检采样路径总长，适应度

(3)

式中：xi、yi分别为第i个采样点的横坐标、纵坐标，xi+1、yi+1分别为第i+1个采样点的横、纵坐标。

PSO的收敛速度取决于ω：ω较大时，算法全局搜索能力较强，适用于全局搜索；ω较小时，算法搜索精度高，更适用于局部搜索。采用PSO求解TSP问题时，1条可能的路径，即按旅行商访问城市的顺序组成的城市序列相当于1个粒子，所有可能的路径相当于粒子种群。用城市序列表示粒子的位置，用交换序列表示粒子速度，通过交换城市位置实现寻优计算过程。

2.2 传统遗传算法

GA模仿自然界中生物体的进化规律，通过复制、杂交、变异将群体逐代进化，通过评估个体的适应度淘汰较差个体，逐步找到最优个体。交叉操作是对父代个体进行基因交换重组，产生新个体，交叉公式为

akj=akj(1-p)+aljp，

alj=alj(1-p)+akjp，

式中：akj为第k条染色体上第j个基因的编码；alj为第l条染色体上第j个基因的编码；p为随机数，p∈ [0,1]。

变异操作类似生物进化过程中的基因突变现象，采用某种方式将染色体中的基因替换为新染色体，增强进化活力，形成新个体。采用GA解决TSP问题时，编码相当于1组城市序列；交叉操作是指交换2组城市序列中的部分城市，形成2组新的城市序列。假设2组城市路径序列编码分别为0 123 456 789，0 546 921 783，若执行交叉操作交换部分编码，得到的2组序列分别为0 126 451 789，0 543 926 783，序列中有重复部分。根据交换的2组基因建立映射关系，通过映射关系将基因“1”转变为基因“3”。重复部分都得到映射后，交叉后的2组路径序列为0 326 451 789和0 543 926 781。变异操作是指将路径序列中的某些城市用该序列中的其他等位城市替换，形成新的路径序列。路径序列0 123 456 789经过突变后变为0 120 456 789，路径中城市编码值“0”重复，缺少码值“3”，故用码值“3”替换码值“0”，得到变异后的路径序列为3 120 456 789。

2.3 结合GA的PSO

为了解决传统PSO易陷入局部最优解，产生早熟收敛等问题，在算法迭代过程中引入交叉、变异操作；为加速算法的收敛，随着迭代次数的增加对ω进行自适应调整，公式为

式中：ωmax、ωmin分别为ω的最大值和最小值，按照经验取ωmax=0.9，ωmin=0.4；tmax为设定的最大迭代次数；t为当前的迭代次数。

改进PSO算法具体步骤包括：1)初始化粒子种群，设定参数；2)计算每个粒子的适应度；3)寻找局部最优Ppbest及全局最优Pgbest；4)根据式(1)(2)计算各个粒子下一时刻的位置及速度；5)引入交叉、变异操作，与Ppbest和Pgbest进行交叉，在位置、速度更新后重新计算适应度，如果路径变短，则保留新的粒子位置，否则舍弃；6)判断是否达到最优解，判断条件包括适应度相对于上一次迭代变小的幅度是否大于设定适应度及是否达到最大迭代次数，若满足判断条件，则寻优结束；若不满足条件，返回步骤2)重复进行。

3 仿真结果

为了验证改进PSO算法的路径规划效果，采用MATLAB软件对路径规划过程进行数值模拟。在50 m×50 m面积的水域范围内，设置50个采样点。分别采用传统PSO、传统GA、改进后的PSO进行全局路径规划。设定粒子种群规模为200，最大迭代次数为500次。

图1、2为采用传统PSO和传统GA做路径规划的仿真示意图和适应度迭代过程。图3、4为改进的PSO做路径规划的仿真示意图和适应度迭代过程。

由图1、2可知：采用传统PSO和传统GA规划的路径，交叉次数较多。算法开始后，随着迭代次数的增加，适应度趋于稳定。经过500次迭代，图2a)、2b)的路径总长分别为606.6、618.2 m。

由图3、4可知：采用改进的PSO规划路径，发生交叉的次数明显减少，经过500次迭代后，得到路径总长为285.3 m。改进算法收敛迅速，路径复杂度大大降低。

a)传统PSO b)传统GA 图1 传统算法的路径规划结果

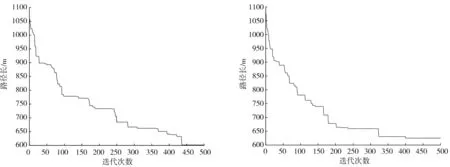
a)传统PSO b)传统GA 图2 传统算法适应度迭代过程

图3 改进的PSO路径规划结果 图4 改进的PSO适应度迭代过程

采用传统PSO、传统GA和改进PSO对不同采样点数进行全局路径规划的结果如表1所示。由表1可知：采用改进的PSO进行规划，比采用传统PSO和GA的路径总长明显变短。

表1 传统PSO、传统GA与改进PSO规划路径总长 m

4 结论

1)采用USV对水域环境进行巡检采样需对USV行驶路线进行路径规划，这就相当于采用智能算法求解旅行商问题。

2)在传统PSO寻优过程中引入交叉、变异思想,增强算法跳出局部最优解的能力，缓解早熟收敛，有效减少路径交叉几率，缩短全局路径总长。

3)在寻优过程中根据迭代次数自适应调整惯性权重，加速算法收敛，缩短USV路径规划的时间，减少计算量。