分布式激励弯曲圆盘换能器研究

师浩然 郝浩琦

（第七一五研究所，杭州，310023）

水声换能器是水中进行电声能量互相转换的装置。由于声波在水下存在传播损失，传播损失中的吸收损失与声波频率正相关，因此为减小吸收损失，增大传播距离，对更低频率的水声换能器的设计研究是必要的[1]。弯曲圆盘换能器辐射阻抗低、辐射面积大，且在众多甚低频换能器设计方案中，弯曲圆盘换能器具有较小的尺寸-频率比。这使其可以较小的几何尺寸、较轻的重量在较低频段范围内工作。弯曲圆盘换能器的结构历经了以二叠片、三叠片为代表的传统弯曲圆盘换能器，到具有空气腔结构的新型弯曲圆盘换能器等。本文以空气腔结构弯曲圆盘换能器为基础，设计了一种分布式激励弯曲圆盘换能器，并利用 ANSYS软件对换能器性能作有限元分析。

1 可行性分析

当前空气腔结构的经典弯曲圆盘换能器模型由John L Delany于2001年提出[2]。采用极化方向相同的两片压电陶瓷外置于金属圆盘两侧，电路上以并联形式连接，工作时两陶瓷片分别发生伸张应变与收缩应变，如图1所示。

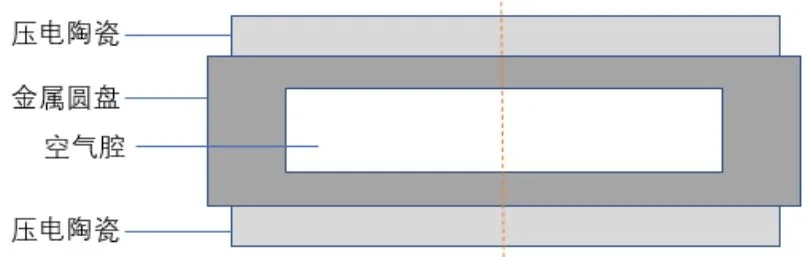
图1 空气腔结构的经典弯曲圆盘换能器

通过瑞利法可以得到三叠片结构弯曲圆盘换能器在空气中谐振频率为[3]：

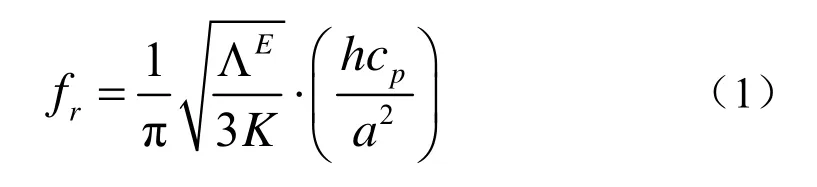
式中，EΛ 为恒压条件下整个弯曲圆盘的有效位能因子，K为动能因子，a为圆盘半径。

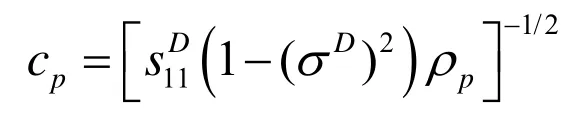
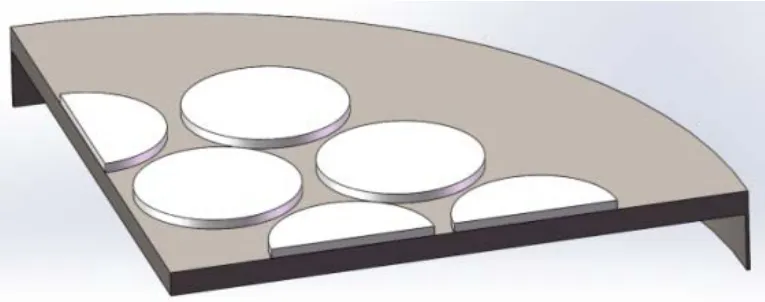
图2 外露分布式弯曲圆盘换能器1/8结构

1.1 模态分析

为验证分布式激励结构可行性，对其做模态分析，并与经典结构作对比。对于弯曲振动圆盘换能器而言，观察其一阶基模即可。根据瑞利法，对无节点圆的基模用幂级数表达假定的弯曲曲线，则法向位移表示为[4]：

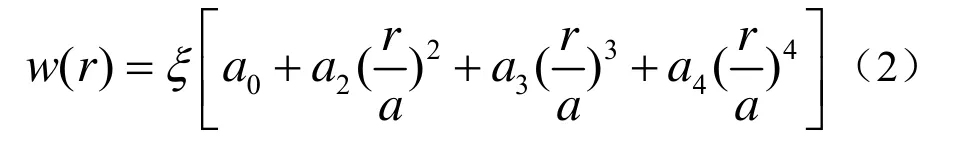
式中，ξ为随时间变化的振幅因子，r为径向坐标，a1～a4为弯曲曲线系数。

分布式激励若能激发同样的振动模态，则可实现与经典弯曲圆盘设计同样的效果。经对比（图3、4），两结构振动模态大体相同。

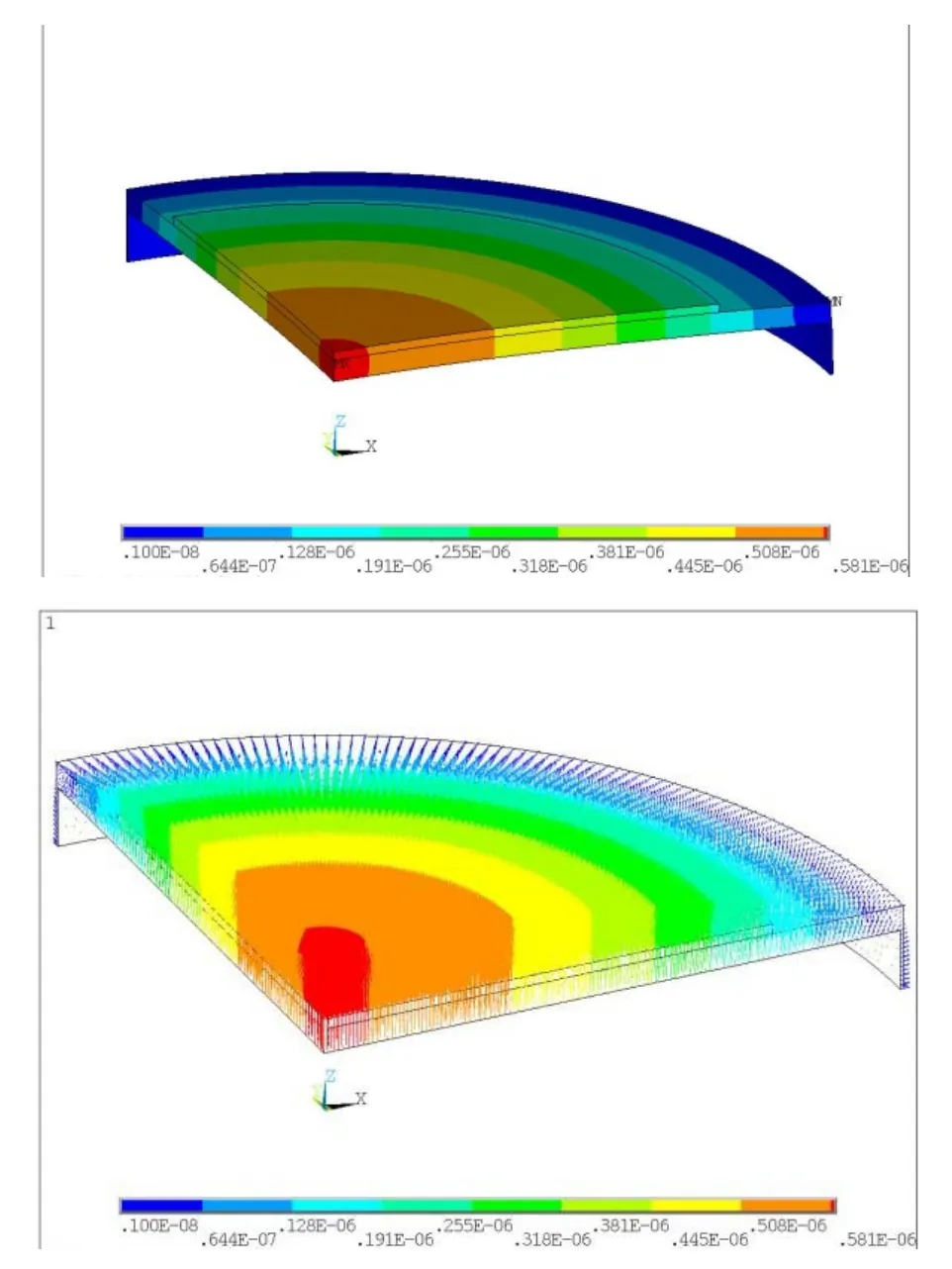
图3 经典结构一阶模态

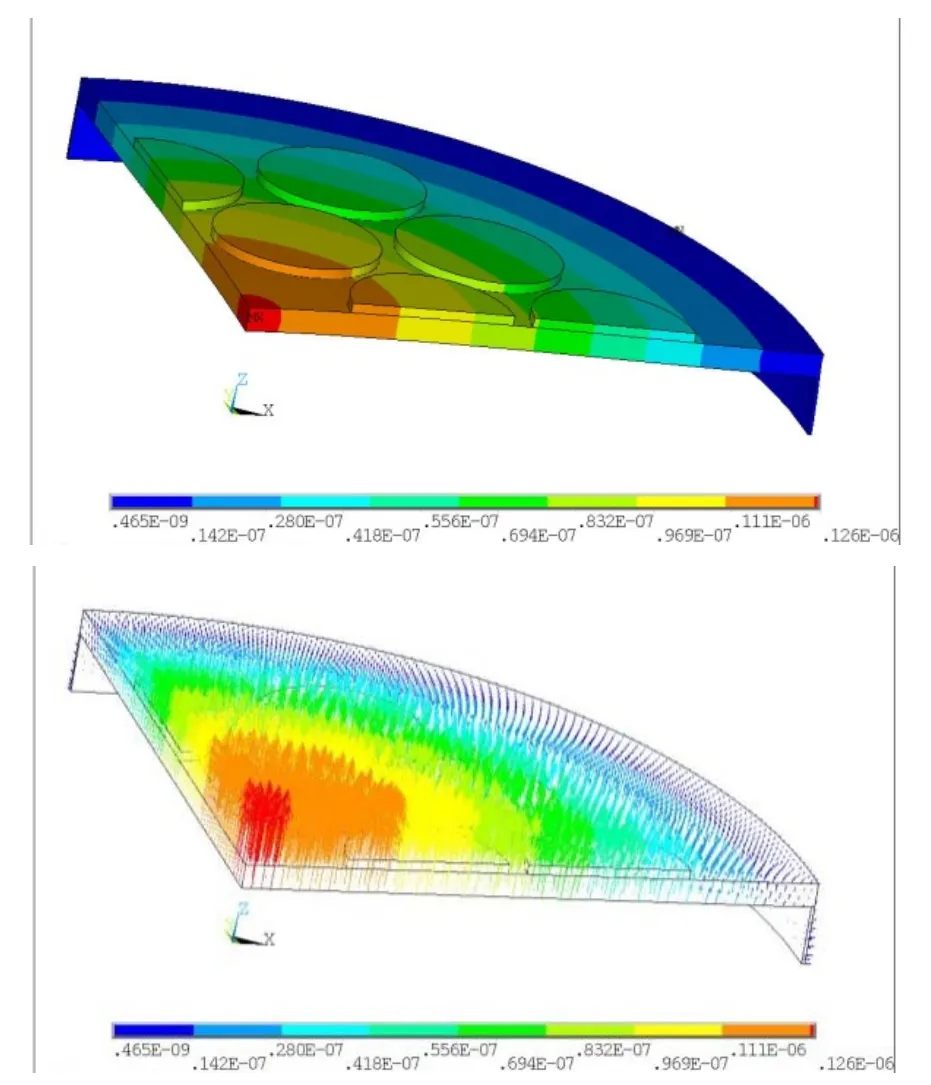
图4 分布式激励一阶模态

1.2 路径位移分析

对于经典弯曲圆盘换能器，因其结构对称性，从圆盘中心出发沿半径到圆盘边缘，任意路径上圆盘位移皆保持一致。但分布化的小圆盘由于排布方式的改变，结构上未必完全对称。为验证分布式激励弯曲圆盘结构是否具有同样规律，选取了四条路径分别对分布式激励弯曲圆盘做位移分析，见图5、6。四条路径两两求相关系数结果均为 0.99。不完全相同的位移曲线证明各个小圆片间存在相互作用，但影响极其微弱。以上两方面验证了多激励方式驱动弯曲圆盘振动机理与经典结构大体相同，即验证了方案的可行性。

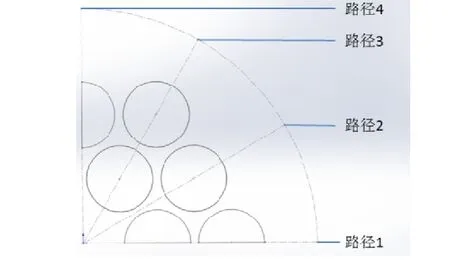
图5 选取的四条重要路径示意图

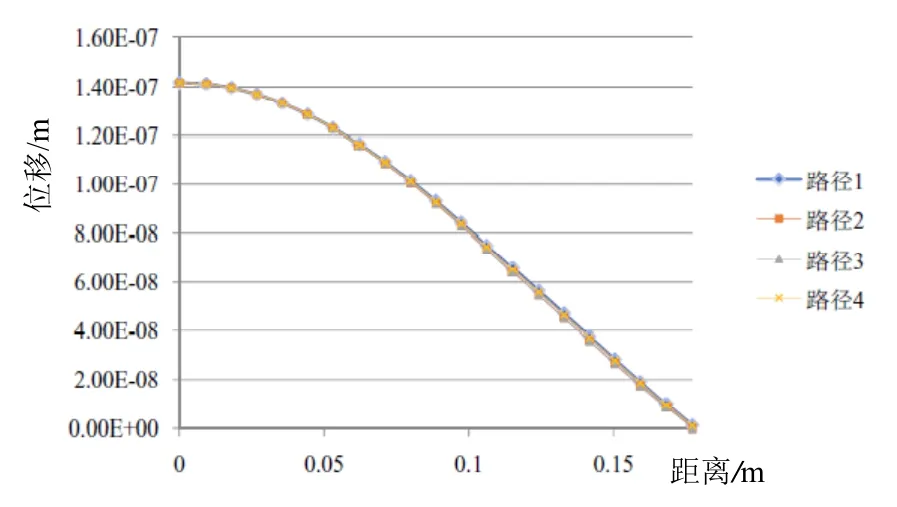
图6 四条路径上圆盘表面厚度方向位移

2 内嵌式换能器结构

薄饼式外形的结构使弯曲圆盘换能器能以较小的几何尺寸、较轻的重量在较低频的频段范围内工作。然而带有空气腔的圆盘结构刚度很低，换能器耐压、抗冲击能力的欠缺会影响其在深水环境的使用。本文采用将陶瓷片内嵌进圆盘金属结构的设计代替现有陶瓷金属盘外露粘合模式，见图7。分别对两种模型弯曲圆盘换能器进行有限元仿真，如图8～9所示。镶嵌结构由于金属增加，整体刚度提升，故谐振频率略有增长，从 180 Hz提升至 207 Hz，而发送电压响应值得到升高，从129.142 dB增加至131.501 dB。谐振频率下，圆盘厚度方向位移也变大。振动性能获得增强。

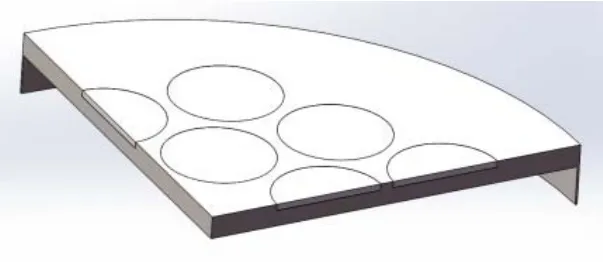
图7 内嵌分布式弯曲圆盘换能器1/8结构

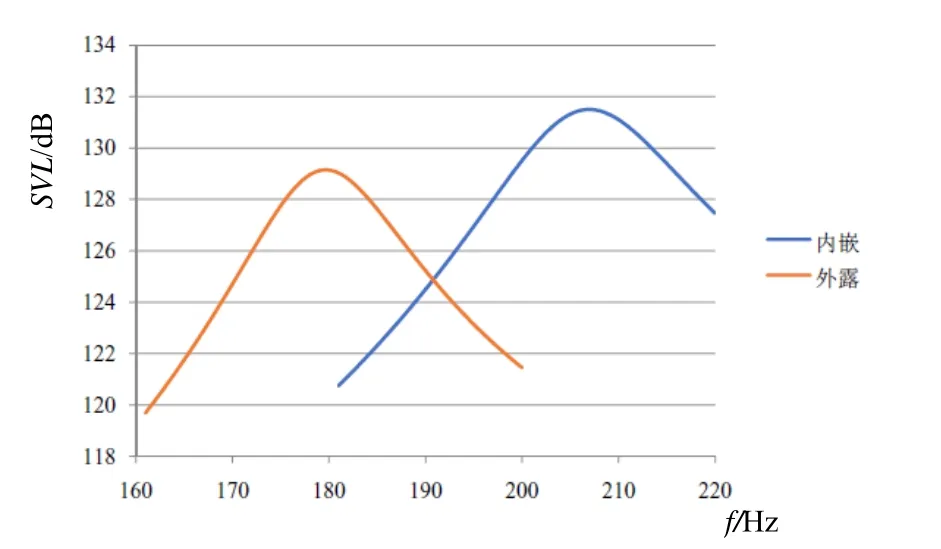
图8 内嵌式结构与外露结构发送电压响应

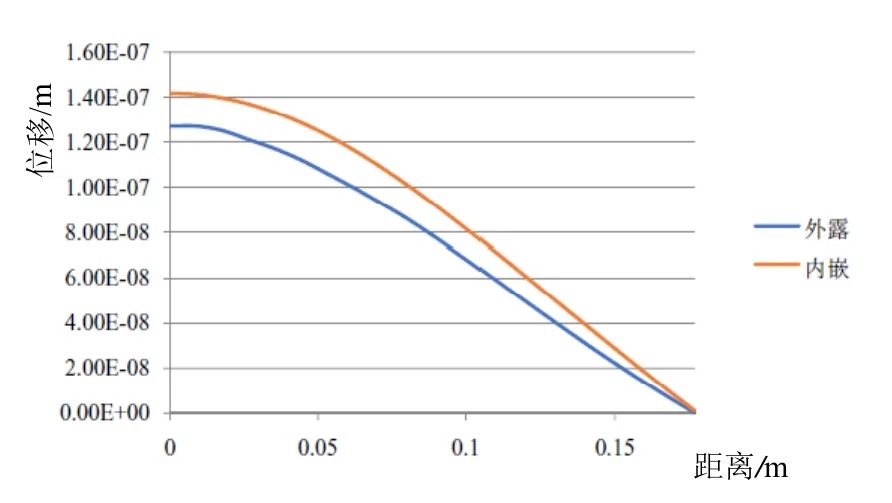
图9 内嵌式结构与外露结构厚度方向位移

3 模型制备与实测

对样机进行制备，实物图见图10。金属弯曲圆盘半径177 mm，空气腔厚度18.25 mm，金属板厚度7.5 mm；压电陶瓷厚度为3 mm。将分布式激励弯曲圆盘换能器用缆绳系好垂下，放置于水下 5 m，对换能器在水中的谐振频率、导纳、发送电压响应进行测量。实测与仿真结果见图11～12。经观察，在水下的电导曲线与发送电压响应曲线趋势与仿真结果接近，谐振频率约 210 Hz，发送电压响应约129 dB。

图10 弯曲圆盘换能器样机

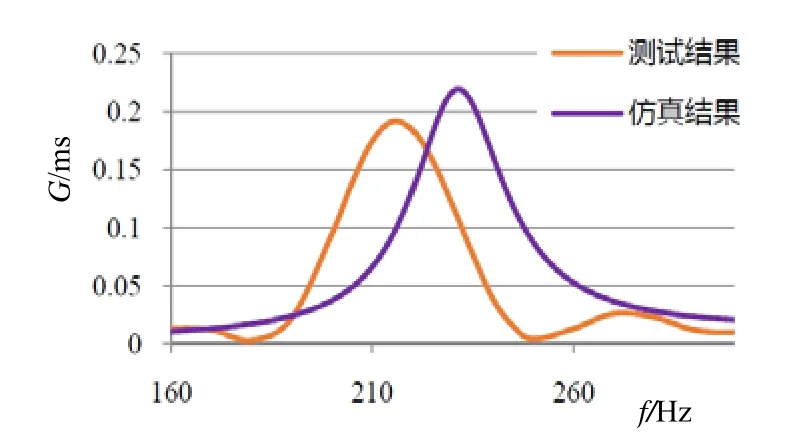
图11 实测水中电导值与仿真结果对比

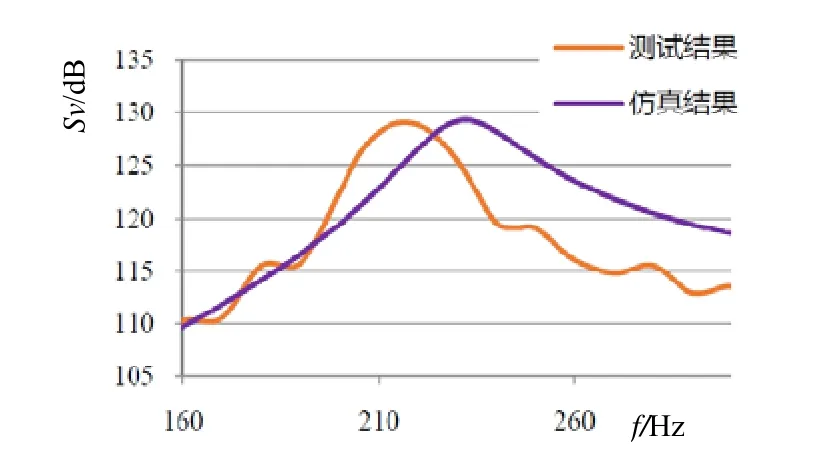
图12 实测水中响应与仿真结果对比

4 结论

本文设计了一种分布式激励弯曲圆盘换能器结构。经由理论验证与有限元分析验证了其可行性。考虑刚度因素，提出内嵌式设计，利用ANSYS有限元分析与外露的经典弯曲圆盘模型对比，发现内嵌式结构的分布式激励弯曲圆盘换能器拥有更佳的振动特性，样机实测获得了与软件仿真相近的结果。在单片分布式弯曲圆盘换能器的研究后，下一步将开展成阵后的多源耦合辐射研究，以实现辐射声功率的提升与带宽扩展。