复合材料矩形悬臂板的稳定性和分岔分析

安凤仙，杨立波

(淮阴工学院 数理学院，江苏 淮安 223001)

复合材料矩形悬臂板因具有轻质、高强度等优点，广泛应用于很多工程领域，比如航天器、发动器和潜水艇等，其动力学方程可以用非线性系统来描述。动力学系统中如果存在非线性因素，就可能会发生分岔现象。非线性动力学系统的分岔问题主要研究局部分岔和全局分岔。局部分岔指的是发生在奇点(或闭轨)的小邻域内，且与它的双曲性破坏相联系的分岔。目前，将高维非线性系统平衡点分岔问题等效地简化为低维系统问题的方法主要有李雅普诺夫-施密特约化(LS约化)、中心流形法以及Galerkin方法[1-2]。近年来，复合材料板的稳定性、分岔和混沌等问题的研究引起了许多学者的关注，Zhao等[3]利用数值模拟方法分析了复合材料矩形悬臂板的混沌运动，得到了系统参数对动力学行为的影响。Akhavan等[4]借助振动模态、Ye等[5]利用多尺度法和数值模拟方法分别探讨了复合材料板的稳定性、分岔和混沌动力学。此外，Guo等[6-9]研究了复合材料压电板的分岔和混沌运动，发现了系统丰富的动力学行为。虽然对于复合材料板的非线性动力学问题有了一系列的研究，但大多采用数值模拟方法，理论分析研究较少。为了更好地设计结构参数，利用理论分析和数值模拟相结合的方法研究复合材料矩形悬臂板的稳定性和分岔行为是非常重要的。

规范型理论在非线性动力学系统的研究中得到了广泛应用，目前主要利用郁培等[10-12]给出的规范型方法分析系统的局部分岔。它的基本思想是引入一个近恒同变换，构造初始微分方程的最简单形式。由于规范型在奇点附近保持了原系统的动力学特性，因此可以利用规范型理论研究原系统的稳定性和局部分岔行为。近来，已经利用Maple等软件得到了求解规范型的计算程序。

本文主要利用理论分析和数值模拟两种方法研究面内激励下超音速气流中复合材料矩形悬臂板的局部动力学行为。利用Maple程序得到了原系统方程的规范型，详细讨论了3种退化平衡点情形下的稳定性、静态分岔、Hopf分岔和2-D圆环面分岔。利用正规型理论得到了系统的稳定性条件以及发生静态分岔、Hopf分岔和2-D圆环面分岔的转迁曲线。此外，应用四阶Runge-Kutta算法对理论分析结果进行数值模拟，验证了理论分析结果的正确性。

1 问题陈述

面内激励下超音速气流中复合材料矩形悬臂板模型如图1所示。板在x和y方向的宽度和长度分别为a和b，厚度为h。在y=0和y=b处沿着y方向的面内激励为F=F0+F1cosωΩ1t，其中Ω1为面内激励的频率。其横向运动的系统方程[3]为：

(1)

其中f表示面内激励的振幅，其他系数详见Zhao等[3]的研究。

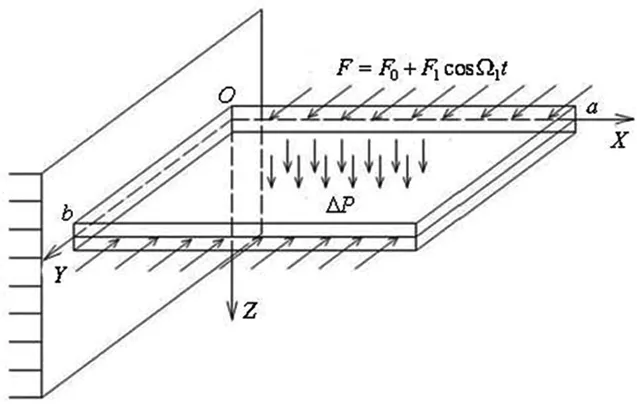
图1 复合材料矩形悬臂板模型

本文主要考虑1:2内共振和主参数共振，共振关系为：

ω22=Ω2+εσ2,Ω1=Ω2=1,

(2)

其中ω1和ω2是线性固有频率，σ1和σ2为调谐参数，利用多尺度法可以得到四维系统方程[3]如下：

(3)

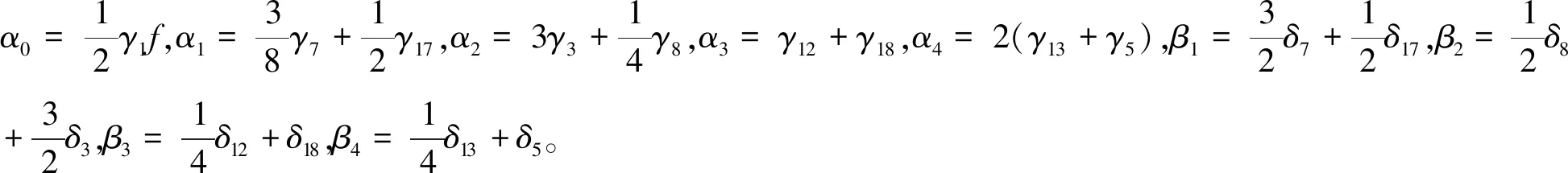
系统方程(3)在初始平衡点(x1,x2,x3,x4)=(0,0,0,0)的Jacobi矩阵为：

(4)

因此可以得到其特征多项式为：

f(λ)=λ4+b1λ3+b2λ2+b3λ+b4

(5)

其中，

b1=μ1+μ2,

(6)

利用Hurwitz准则[2]，可得到初始平衡点(x1,x2,x3,x4)=(0,0,0,0)的渐近稳定性条件为：

(7)

相应地，如果条件(7)不满足，则初始平衡点失去稳定性，系统(3)可能会发生分岔。下面将分3种情形详细讨论当条件(7)不满足时系统方程(3)的稳定性和分岔行为。

2 稳定性和分岔分析

阻尼系数通常会对系统的动力学行为产生重要的影响。因此，在以下3种情况分析中选择系统参数μ1和μ2作为扰动参数。

2.1 一对纯虚特征根

β4=1，则b1=b2=b3=3，b4=2。特征多项式(5)的特征根为λ1,2=±i，λ3=-1，λ4=-2。

选择μ1和μ2为扰动参数，利用参数变换μ1=3+ζ1，μ2=ζ2，则特征多项式(5)变换为：

(8)

其中，

(9)

因此，可以得到初始平衡点(x1,x2,x3,x4)=(0,0,0,0)的稳定性条件为：

(10)

即：

ζ1+ζ2+3>0,

(11)

由不等式(11)可以得到4条转迁曲线Li(i=1,2,3,4)，如图2所示。

图2 一对纯虚特征根时的转迁曲线

L1:ζ1+ζ2+3=0,

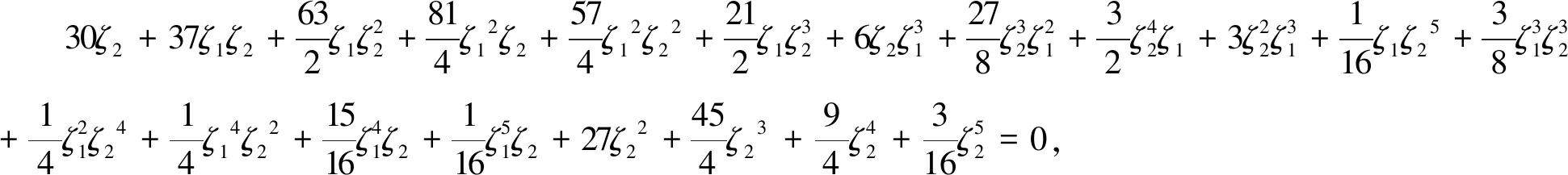
(12)

显然，参数ζ1和ζ2取值于区域I时，初始平衡点(E.S.)是稳定的，而当参数ζ1和ζ2从区域II中取值时，系统发生分岔，产生了稳定的极限环。

基于系统方程(3)，利用四阶Runge-Kutta算法进行数值模拟。在区域I中取参数值为(ζ1,ζ2)=(0.1,0.1)时，从初始点(x1,x2,x3,x4)=(0.02,-0.01,0.01,-0.02)出发的数值解收敛于原点，说明初始平衡点渐近稳定(见图3)。在区域II中取参数值(ζ1,ζ2)=(-0.2,-0.2)，初始点(x1,x2,x3,x4)=(-0.01,0.02,0.03,-0.02)时，系统发生分岔，产生了稳定的极限环(见图4)。

图3 当(ζ1,ζ2)=(0.1,0.1)，(x1,x2,x3,x4)=(0.02,-0.01,0.01,-0.02)时，平面(x1,x2)和(x3,x4)内的相图

图4 当(ζ1,ζ2)=(-0.2,-0.2)，(x1,x2,x3,x4)=(-0.01,0.02,0.03,-0.02)时，平面(x1,x2)和(x3,x4)内的相图

2.2 一个零特征根和一对纯虚特征根

(13)

则系统方程(3)变换为：

(14)

当ζ1c=ζ2c=0时，系统(14)在初始平衡点(z1,z2,z3,z4)=(0,0,0,0)的Jacobi矩阵为：

(15)

其在临界点附近的动力学行为和z1，z2以及z3有关。引入近恒等非线性变换zi=yi+gi(yi)及变换y1=y，y2=rcosθ，y3=rsinθ，y4=y4，可得系统(14)的规范型为：

(16)

且有：

(17)

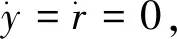
(1)初始平衡点(E.S.)：y=r=0，

(3)一次Hopf分岔解 (H.B.(I))：y=0，

方程(16)的Jacobi矩阵为：

(18)

依据Jacobi矩阵(18)来讨论以上4个平衡解的稳定性和分岔行为。

由E.S.对应的Jacobi矩阵，可以得到其稳定性条件为：

ζ1>0,ζ2>0

(19)

对应的参数区域如图5所示，区域的两条临界曲线为L5：ζ1=0(ζ2>0)和L6：ζ2=0(ζ1>0)。通过分析可知，初始平衡点通过转迁曲线L5分岔出静态分岔解，根据对应的Jacobi矩阵可以确定静态分岔解的稳定性条件为：

ζ1<0，3ζ1+ζ2>0

(20)

于是得到另外一条边界曲线为L7：3ζ1+ζ2=0(ζ1<0)。

计算H.B.(I)的Jacobi矩阵，有：

(21)

则当条件(22)满足时，H.B.(I)是稳定的，稳定区域的边界曲线为L6和L8：ζ1-2ζ2=0(ζ2<0)。

-ζ1+2ζ2<0，ζ2<0

(22)

当-ζ1+2ζ2>0且3ζ1+ζ2<0时，分岔出H.B.(II)，为了研究H.B.(II)的稳定性，计算其对应的Jacobi矩阵为：

(23)

因此，稳定性条件为：

(24)

显然，条件Det=112y2r2>0恒成立。根据以上分析，则H.B.(II)稳定区域的边界曲线是L7和L8。分岔曲线如图5所示。

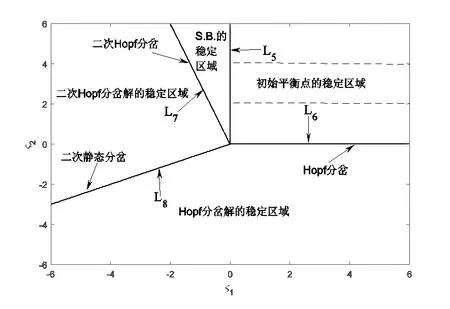
图5 一个零特征根和一对纯虚特征根时的转迁曲线

类似地，从图5中不同区域选取参数值来验证以上理论分析结果。分别在4个平衡点稳定区域取参数值(ζ1,ζ2)=(0.1,0.1)、(ζ1,ζ2)=(-0.05,0.2)、(ζ1,ζ2)=(0.2,-0.2)及(ζ1,ζ2)=(-0.1,0.2)，从初始点(x1,x2,x3,x4)=(0,-0.01,0,0.01)、(x1,x2,x3,x4)=(0.04,-0.05,-0.01,0.02)、(x1,x2,x3,x4)=(0.01,0,0,-0.02)及(x1,x2,x3,x4)=(0.5,-0.4,-0.2,0.2)出发的数值解分别收敛于原点、静态分岔解以及出现了稳定极限环(见图6～图9)。从图6～图9可以发现，所有数值结果和理论结果一致，表明了理论分析的正确性。

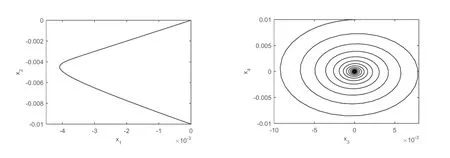
图6 当(ζ1,ζ2)=(0.1,0.1)，(x1,x2,x3,x4)=(0,-0.01,0,0.01)时，平面(x1,x2)和(x3,x4)内的相图

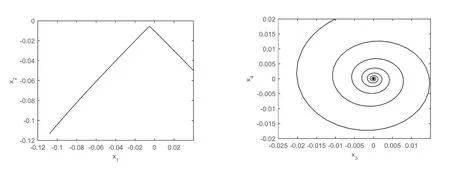
图7 当(ζ1,ζ2)=(-0.05,0.2)，(x1,x2,x3,x4)=(0.04,-0.05,-0.01,0.02)时，平面(x1,x2)和(x3,x4)内的相图

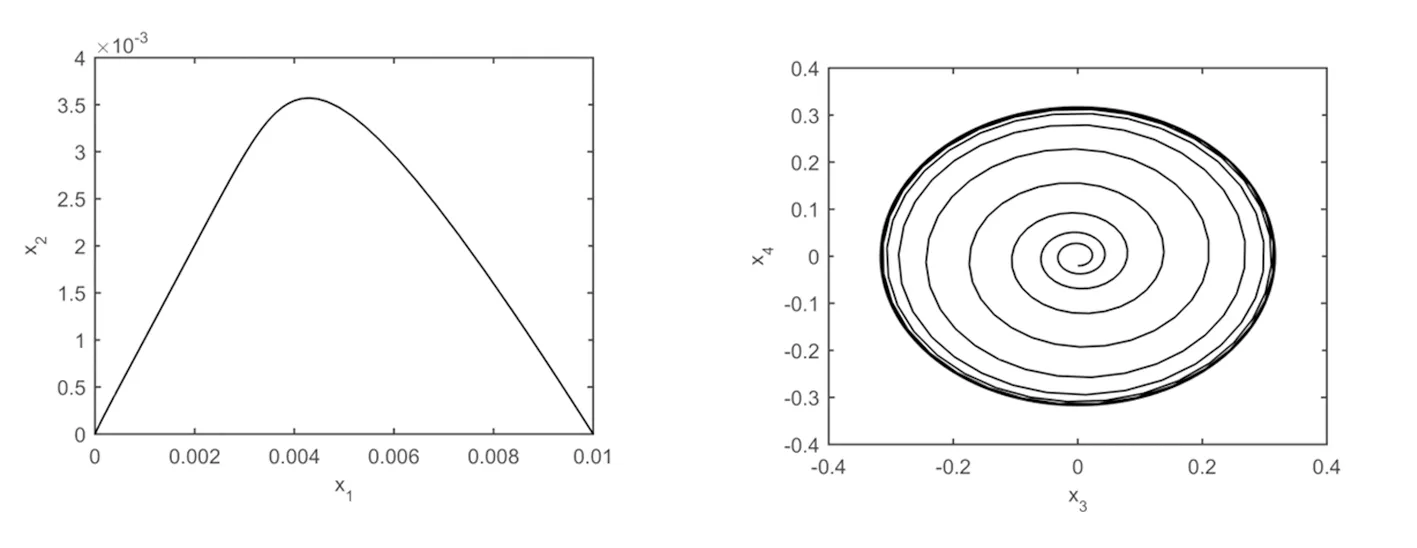
图8 当(ζ1,ζ2)=(0.2,-0.2)，(x1,x2,x3,x4)=(0.01,0,0,-0.02)时，平面(x1,x2)和(x3,x4)内的相图

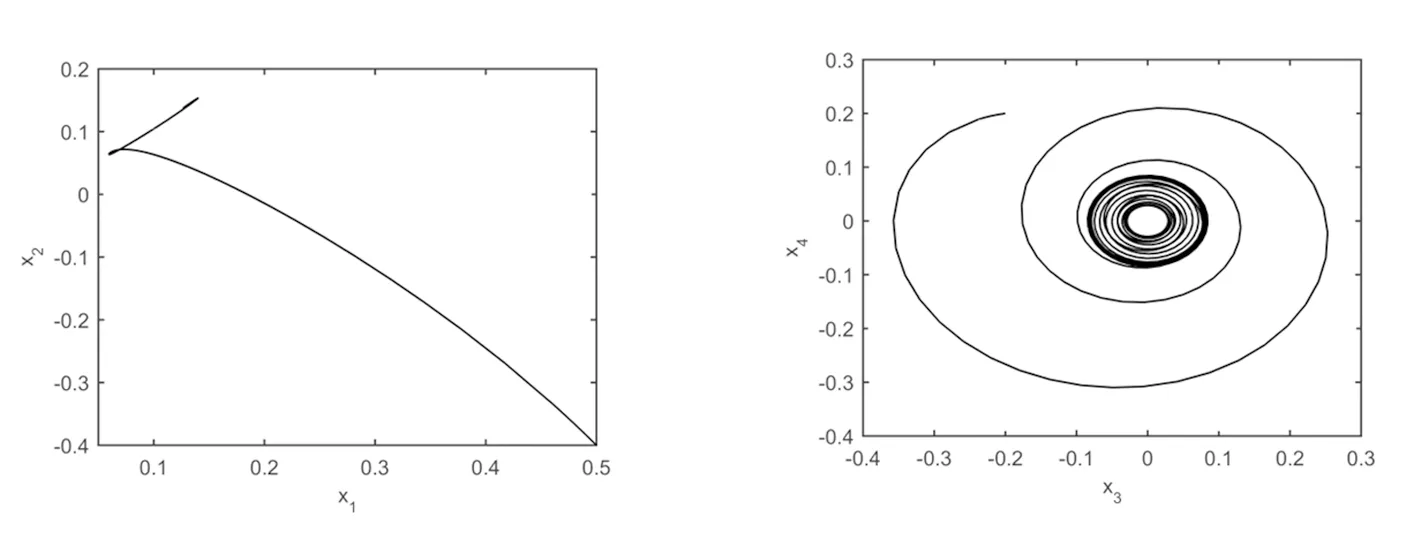
图9 当(ζ1,ζ2)=(-0.1,0.2)，(x1,x2,x3,x4)=(0.5,-0.4,-0.2,0.2)时，平面(x1,x2)和(x3,x4)内的相图

2.3 两对纯虚特征根

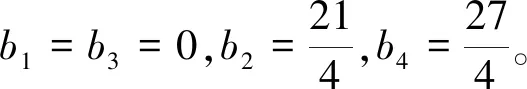
(25)

方程(3)变换为：

(26)

令ζ1c=ζ2c=0，系统(26)在初始平衡点(z1,z2,z3,z4)=(0,0,0,0)的Jacobi矩阵为

(27)

同时利用线性变换zi=yi+gi(yj)及变换y1=r1cosθ1，y2=r1sinθ1,y3=r2cosθ2，y4=r2sinθ2，可以得到系统方程(26)的规范型为：

(28)

且有：

(29)

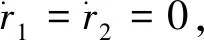
(1)初始平衡点 (E.S.)：r1=r2=0，

(2)一次Hopf分岔解(H.B.(I))：

(3)二次Hopf分岔解(H.B.(II))：

(4)拟周期解(2-D tori)：

方程(28)的Jacobi矩阵为：

(30)

类似于2.2的分析方法，根据Jacobi矩阵(30)，可以得到E.S.、H.B.(I)和H.B.(II)的稳定区域分别为(1)ζ1>0，ζ2>0；(2)ζ1<0 ，2ζ1+ζ2>0；(3)ζ1-ζ2>0，ζ2<0。同时发现，只要存在2-D圆环面，都是稳定的。稳定区域对应的转迁曲线分别记为L9：ζ1=0(ζ2>0)、L10：ζ2=0(ζ1>0)、L11：2ζ1+ζ2=0以及L12：ζ1-ζ2=0，如图10所示。

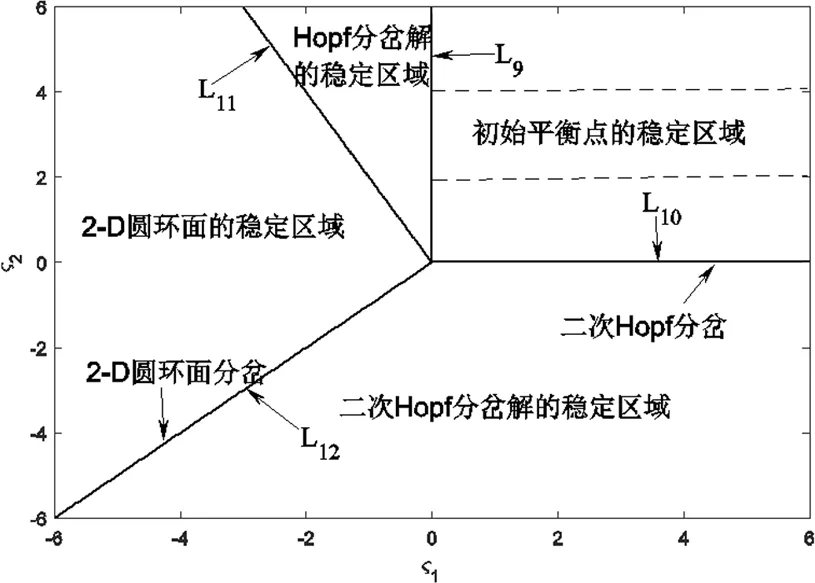
图10 两对纯虚特征根时的转迁曲线

从图10中平衡点的稳定区域分别选取参数值来验证理论分析结果。参数取值(ζ1,ζ2)=(0.1,0.1)、(ζ1,ζ2)=(-0.1,0.3)、(ζ1,ζ2)=(0.1,-0.1)及(ζ1,ζ2)=(-0.0001,0.0001)，由数值模拟结果可以发现从初始点(x1,x2,x3,x4)=(0,0.01,0,-0.02)、(x1,x2,x3,x4)=(0.05,0.02,0.01,-0.01)、(x1,x2,x3,x4)=(0.02,-0.01,0.01,-0.02)及(x1,x2,x3,x4)=(0.01,0.03,-0.03,0.01)出发的数值解分别收敛于原点、出现了稳定极限环和2-D圆环面，如图11～图14所示。

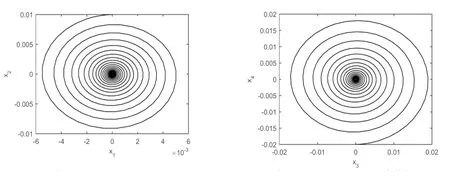
图11 当(ζ1,ζ2)=(0.1,0.1)，(x1,x2,x3,x4)=(0,0.01,0,-0.02)时，平面(x1,x2)和(x3,x4)内的相图

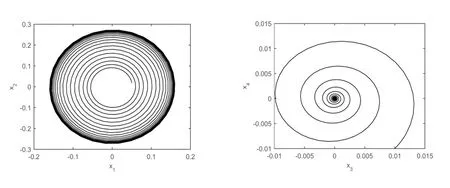
图12 当(ζ1,ζ2)=(-0.1,0.3)，(x1,x2,x3,x4)=(0.05,0.02,0.01,-0.01)时，平面(x1,x2)和(x3,x4)内的相图

图13 当(ζ1,ζ2)=(0.1,-0.1)，(x1,x2,x3,x4)=(0.02,-0.01,0.01,-0.02)时，平面(x1,x2)和(x3,x4)内的相图

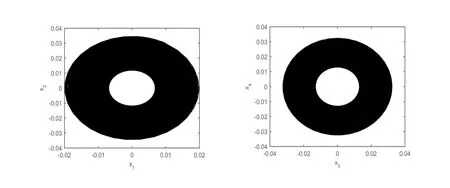
图14 当(ζ1,ζ2)=(-0.0001,0.0001)，(x1,x2,x3,x4)=(0.01,0.03,-0.003,0.01)时，平面(x1,x2)和(x3,x4)内的相图

3 结论

本文主要研究了面内激励下超音速气流中复合材料矩形悬臂板的动力学行为，详细讨论了3种退化平衡点的稳定性和分岔行为。选取μ1和μ2为扰动参数，利用参数变换和状态变量变换，得到了平衡点的稳定性条件和稳定区域。利用规范型理论，确定了系统发生静态分岔、Hopf分岔和2-D圆环面分岔的转迁曲线，应用四阶Runge-Kutta算法对所有理论分析结果进行数值模拟，验证了理论分析结果的正确性。从数值模拟结果可以发现，当系统参数μ1、μ2和初始条件取不同值时，系统的相图不同，说明系统阻尼系数和初始条件对复合材料矩形悬臂板的动力学行为有较大的影响。因此，可以通过改变系统参数来控制系统的非线性振动。在航天器、汽车和潜水艇等进行结构设计时，需要考虑因结构参数可能会表现出的显著非线性动力学行为，本文的研究结果对于复合材料矩形悬臂板等一些力学系统的特性分析及设计具有一定的参考价值。