有向部分半群作用下的敏感性

曾眺英

(嘉应学院数学学院， 梅州 514015)

称偶对(X,f)是一个拓扑动力系统(简称动力系统)，如果X是紧致度量空间，f:X→X是连续映射． 自LI和YORKE[1]首次提出混沌的定义以来，系统的复杂性一直是拓扑动力系统研究的重要课题．

初值敏感是Devaney混沌定义中的核心，精略地说就是在任意非空开集中存在2个不同点，它们的轨道至少在某个时刻分开的距离是给定的正数长． 2005年，熊金城[2]给出了n-敏感的定义，精略地说就是在任意非空开集中存在n个不同点，两两之间的轨道至少在某个时刻分开的距离是给定的正数长． 多年以来，学者们致力于敏感性和n-敏感性的研究． 如：张瑞丰[3]证明了对于一个拓扑动力系统(X,f)，设X是局部连通空间，如果(X,f)是敏感的，那么它是n-敏感的；YE和ZHANG[4]给出了相对于集合初值敏感、初值敏感集和局部proximal集的定义，证明了一个传递系统是敏感的当且仅当存在一个敏感集S且Card(S)≥2，并且传递系统的任意敏感集都是局部proximal集．

近年来，半群作用下的敏感性及其相关概念的研究得到了许多学者的关注[5-9]． 例如：EDUARD和MICHAEL[5]研究了一般半群作用下的敏感性，证明了如果S是C-半群且(X,d)是一个传递的PolishS-系统，那么系统(S，X)是几乎等度连续的当且仅当它不是敏感的；IGLESIAS和PORTELA[6]证明了半群作用下的动力系统如果是几乎开的，那么该系统是敏感的或者该系统的等度连续集是一个剩余集；LI等[7]研究了半群作用下的敏感函数和等度连续函数，证明了一个传递系统是敏感的当且仅当该系统具有敏感偶对，或者说该系统具有一个敏感函数．

事实上，在不同类型的半群作用下的动力系统表现出来的复杂性也不同. 2016年，FARMAKI等[10]研究了有向部分半群作用下的拓扑动力系统，在一些限定条件下得到了关于有向部分半群作用的多重回复性定理，指出了IP-系统[11]和以词为索引的拓扑动力系统[12]都是关于有向部分半群作用下的拓扑动力系统的具体例子；同时，FARMAKI等[13]得到了有向集上余理想的Nash-Williams型定理，拓展了经典的拓扑Ramsey定理． 受文献[10]、[13]的启发，本文研究了有向部分半群作用下的敏感性和n-敏感性，试图找到Λ-拓扑动力系统中敏感性和n-敏感性的等价刻画，进一步给出有向部分半群作用下的Λ-拓扑动力系统中敏感性和n-敏感性之间的关系．

1 预备知识

对于非空集合A，用Card(A)表示集合A的基数． 对于拓扑空间X，用Xn表示n次乘积空间X×X×…×X． 记Δn={(x,x,…,x)Xn:xX}且Δ(n)={(x1,x2,…,xn)Xn:∃i≠j,使得xi=xj}．

定义1[14]设X是一个度量空间，f:X→X是连续映射，如果f满足下面的条件：

(1)f是传递的；

(2)f的周期点在X中稠密；

(3)f是初值敏感的，

则称f是X上的Devaney混沌.

下面介绍有向部分半群、有向部分半群作用下的适配余理想基以及以部分半群为索引的拓扑动力系统的定义．

定义2[10]设Λ是一个非空无限集且是Λ上的关系，如果满足下面的条件:

(1)当λ1,λ2Λ且λ1λ2时，有λ1≠λ2；

(2)当λ1,λ2,λ3Λ，且满足λ1λ2且λ2λ3时，有λ1λ3；

(3)对任意λ1,λ2Λ，存在λ3Λ，使得λ1λ3且λ2λ3，

则称(Λ,)是一个有向集．

本文总假设Λ是可数集．

定义3[10]设(Λ,)是一个无限的有向集． 如果[Λ]∞的子集R满足下面的3条性质：

(1)对任意AR和λ1Λ，存在λ2A，使得λ1λ2；

(2)当A∪BR时，有AR或者BR；

(3)当AR且A⊆B⊆X时，有BR，

则称R是(Λ,)上的一个余理想.

设(Λ,)是一个无限的有向集，A⊆Λ且λΛ,则A-λ={zA:λz}．

注1设(Λ,)是一个无限的有向集，I是Λ上的一个超滤子.如果对任意AI以及λΛ，满足A-λ≠∅，那么超滤子I是(Λ,)上的余理想，且在Λ上的这种超滤子的并集也是(Λ,)上的余理想．

定义4[10]设(Λ,)是一个无限的有向集． 如果[Λ]∞上的子集满足下面的2条性质：

(1)对任意A和λ1Λ，存在λ2A，使得λ1λ2；

(2)当A∪B时，存在C，使得C⊆A或C⊆B，

容易看出(Λ,)上的余理想是(Λ,)上的余理想基．

定义5[10]设(Λ,)是一个无限的有向集． 如果Λ上的算子*满足下面的条件：对任意满足λ1λ2λ3的λ1,λ2,λ3Λ，有λ1λ2*λ3、λ1*λ2λ3且(λ1*λ2)*λ3=λ1*(λ2*λ3)，则称(Λ,,*)是一个有向部分半群．

定义6[10]设(Λ,,*)是一个有向部分半群，是(Λ,)上的一个余理想基. 对于任意B，对任意λ1,λ2B，若当λ1λ2时，有λ1*λ2B，则称是相对于(Λ,,*)适配的.

定义7[10]设(Λ,,*)是一个有向部分半群. 称由紧致度量空间(X,d)到自身的连续映射构成的集族是一个X上的Λ-拓扑动力系统，如果对任意λ1,λ2Λ，λ1λ2,有

本文记X上的Λ-拓扑动力系统为(X,{Tλ}λΛ)．

注2(1)若是(Λ,,*)的一个适配余理想基且B，则集族(X,{Tλ}λB)也是X上的一个拓扑动力系统．

(2)设T是从紧致度量空间X到自身的连续映射，则(X,{Tλ}λ+)也是X上的一个+-拓扑动力系统． 如果对任意λ1,λ2Λ，有则称这个Λ-拓扑动力系统是可交换的．

定义8[10]设(Λ,,*)是一个有向部分半群，(X,{Tλ}λΛ)是X上的Λ-拓扑动力系统，是(Λ,,*)上的一个适配余理想基且B. 对X中的点x0，如果存在A且A⊆B，使得λ(x0)=x0，则称x0是B-回复点．

2 有向部分半群作用的初值敏感性

本节研究在有向部分半群作用下的紧致度量空间到自身的Λ-拓扑动力系统中的敏感性，得到了关于初值敏感的一些性质．

下面给出拓扑传递性以及等度连续的相关定义.

定义9设(Λ,,*)是一个有向部分半群，(X,{Tλ}λΛ)是紧致度量空间(X,d)上的Λ-拓扑动力系统，是(Λ,,*)上的一个适配余理想基且B. 那么

(1)如果对任意非空开集U、V，存在λΛ，使得U∩Tλ(V)≠∅，则称(X,{Tλ}λΛ)是拓扑传递的．

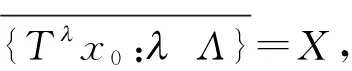
(3) 设x0X. 如果对任意xX，存在A且A⊆B，使得λ(x)=x0，则称点x0为B传递点． 显然每个B-传递点都是B-回复点,记全体B-传递点的集合为TransB(X).

定义10设(X,{Tλ}λΛ)是一个Λ-拓扑动力系统,那么

(1)设A⊆{Tλ}λΛ. 如果对任意ε>0，存在δ>0，使得d(x0,x)<δ时，有d(Tλ(x0),Tλ(x))<ε对任意TλA(λΛ)成立，则称子集A作用在x0X上是等度连续的；如果A作用在任意x0X上是等度连续的，则称A作用在X上是等度连续的.

(2)如果A∶={Tλ}λΛ作用在点x0X上是等度连续的，则称点x0是等度连续点，记Eq(X)为等度连续点的全体. 如果Eq(X)=X，则称(X,{Tλ}λΛ)是等度连续的.

性质1设X是紧致度量空间，(Λ,,*)是有向部分半群，且(X,{Tλ}λΛ)是一个Λ-拓扑动力系统，则(X,{Tλ}λΛ)具有稠密的传递点集当且仅当它是拓扑传递的.

证明假设系统(X,{Tλ}λΛ)具有稠密的传递点集．U和V是X的非空开集，选取传递点yV，则存在λΛ，使得Tλ(y)U，可得U∩Tλ(V)≠∅.

现在假设(X,{Tλ}λΛ)是传递系统. 对任意非空开集U⊂X，集合在X中稠密. 由于X是紧致度量空间，对于给定拓扑，存在一个可数基，使得}是X的稠密集且这个集合的任意点都是X的传递点. 证毕.

性质2设X是紧致度量空间，(Λ,,*)是有向部分半群且(X,{Tλ}λΛ)是一个Λ-拓扑动力系统. 如果(X,{Tλ}λΛ)是拓扑传递的，那么Eq(X)⊂Trans(X)．

证明设x0Eq(X)且任取yX. 对任意给定的ε>0，记Bε(y)∶={xX:d(x,y)<ε}是y的ε-邻域． 因为x0Eq(X)，则存在x0的邻域U，使得对任意λΛ和xU，有d(Tλ(x0),Tλ(x))<ε/2. 由于(X,{Tλ}λΛ)是拓扑传递的，则存在λ0Λ，使得Tλ0(U)∩Bε/2(y)≠∅． 因此，存在xU，有d(Tλ0(x),y)<ε/2，这就意味着d(Tλ0(x0),y)<ε. 证毕.

定义11[10]设X是一个紧致度量空间，(Λ,,*)是有向部分半群，且(X,{Tλ}λΛ)是一个Λ-拓扑动力系统. 对X中的非空闭子集B，如果对任意λΛ，B都是Tλ-不变的，则B=X，那么称系统(X,{Tλ}λΛ)是极小的．

由定义11，易得以下结论：

性质3设X是紧致度量空间，(Λ,,*)是有向部分半群且(X,{Tλ}λΛ)是一个Λ-拓扑动力系统． 则下面命题等价：

(1)(X,{Tλ}λΛ)是极小系统；

(2)对任意xX，集合{Tλ(x):λΛ}是X的稠密集；

(3)对X的任意非空开集U，存在有限多个元素λ1,…,λnΛ，使得

下面给出C-系统的定义．

定义12设(Λ,,*)是有向部分半群，(X,{Tλ}λΛ)是一个Λ-拓扑动力系统． 如果{Tλ}λΛ是一个拓扑半群且对任意λ0λ0)在(X,{Tλ}λΛ)中是相对紧致(即它的闭包紧致)的，则称(X,{Tλ}λΛ)是C-系统．

引理1[5]设(X,S)是拓扑半群作用的动力系统，其中(X,d)是紧致度量空间. 设A⊂S是相对紧致的集合，那么A作用在(X,d)上是等度连续的.

性质4设(Λ,,*)是有向部分半群，(X,{Tλ}λΛ)是一个可交换的C-系统. 假设(X,{Tλ}λΛ)是点传递系统且Eq(X)≠∅，则任意传递点都是等度连续点，即Trans(X)⊂Eq(X).

证明设y是传递点且xEq(X)是等度连续点. 对给定的ε>0，存在x的邻域U(x)，使得对任意λΛ和任意x′,x″U(x)，有d(Tλ(x′),Tλ(x″))<ε. 因为y是传递点，则存在λ0Λ，有Tλ0(y)U(x). 由于(Tλ0)-1U(x)是y的一个邻域，则对任意λΛ和任意y′,y″(Tλ0)-1U(x)，有d(Tλ(Tλ0(y′)),Tλ(Tλ0(y″)))<ε．

因为(X,{Tλ}λΛ)是一个C-系统，则集合M∶=是紧致集． 因此，由引理1可知M⊂{Tλ}λΛ是X的等度连续集． 选取y的邻域V(y)，使得对任意TλM和任意y′,y″U(x)，有d(Tλ(y′),Tλ(y″))<ε，则W∶=(Tλ0)-1U(x)∩V(y)是y的邻域．

性质5设(Λ,,*)是有向部分半群，(X,{Tλ}λΛ)是一个可交换的Λ-系统． 假设(X,{Tλ}λΛ)是极小的C-系统且Eq(X)≠∅，则X是等度连续的．

证明如果(X,{Tλ}λΛ)是极小系统，那么Trans(X)=X． 如果Eq(X)≠∅，由性质4可知X中的点都是等度连续点，则有Eq(X)=X. 证毕.

对于Λ-拓扑动力系统(X,{Tλ}λΛ)，如果集合Eq(X)在X中稠密，则称该系统是几乎等度连续的．下面给出一个几乎等度连续的等价命题．

性质6设(Λ,,*)是有向部分半群，(X,{Tλ}λΛ)是一个可交换的Λ-拓扑动力系统． 假设(X,{Tλ}λΛ)是拓扑传递的C-系统，则X是几乎等度连续的当且仅当Eq(X)≠∅．

证明如果X是几乎等度连续的，显然Eq(X)≠∅. 现在假设(X,{Tλ}λΛ)是拓扑传递的，则由性质1可知Trans(X)是X的稠密集． 如果Eq(X)≠∅，则由性质4可得Trans(X)⊂Eq(X)． 因此，Eq(X)是X的稠密集，即X是几乎等度连续的. 证毕.

下面给出敏感的Λ-拓扑动力系统的定义.

定义13设(X,{Tλ}λΛ)是一个Λ-拓扑动力系统. 如果存在ε>0，对任意xX和x的任意邻域U，存在yU和λΛ，使得d(Tλx,Tλy)>ε，则称(X,{Tλ}λΛ)是敏感的. 此时称ε是一个敏感常数.

下面给出有向部分半群作用下的Λ-拓扑动力系统是几乎等度连续的等价刻画.

定理1设(Λ,,*)是有向部分半群，(X,{Tλ}λΛ)是一个可交换的Λ-拓扑动力系统. 假设(X,{Tλ}λΛ)是拓扑传递的C-系统，则X是几乎等度连续的当且仅当它不是敏感的．

证明由定义13易知，如果X是几乎等度连续的,则X一定不是敏感的. 现在假设X不是敏感的，则对任意k+，存在非空开集Uk⊂X，使得对任意(λ,k)Λ×+，有diam(Tλ(Uk))<1/k成立. 令且W∶=∩k+Vk. 由传递性可知，对X的任意非空开集U，存在λΛ，使得U∩(Tλ)-1Vk≠∅． 由于{Tλ}λΛ是可交换的，则任意Vn都是X的稠密集． 由Baire定理[15]可知W也在X中稠密．

下面证明W⊂Eq(X)成立. 设xW且ε>0，选取足够大的k+，使得1/k<ε，则存在k+，使得xVk，这就意味着存在λ0Λ，满足Tλ0(x)Uk. 设U0=(Tλ0)-1Uk，则对于任意yU0和任意Tλ有

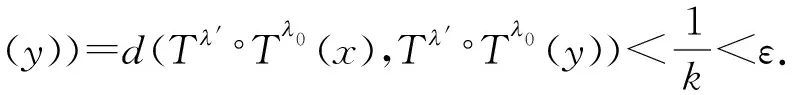
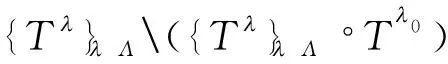
称一个映射是半开的，如果任意非空开集的像集包含非空开子集. 称2个Λ-拓扑动力系统之间的映射π:(X,{Tλ}λΛ)→(Y,{Tλ}λΛ)是因子映射，如果π是连续的满射,且对任意λΛ,满足Tλ下面说明敏感性可以被因子映射所提升．

性质7设(X,d)和(Y,d)是紧致度量空间，(X,{Tλ}λΛ)和(Y,{Tλ}λΛ)是Λ-拓扑动力系统，且π:(X,{Tλ}λΛ)→(Y,{Tλ}λΛ)是一个半开的因子映射． 如果(Y,{Tλ}λΛ)是敏感的，那么(X,{Tλ}λΛ)也是敏感的．

证明设ε是系统(Y,{Tλ}λΛ)的一个敏感常数． 因为π连续，则存在δ>0，使得d(π(x),π(y))>ε时，有d(x,y)>δ．

设U是X的非空开集. 由于π是半开映射，则π(U)包含了Y的一个非空开集V. 因为(Y,{Tλ}λΛ)是敏感的，则存在λΛ及y1,y2V，使得d(Tλ(y1),Tλ(y2))>ε. 选取x1,x2U，使得π(x1)=y1,π(x2)=y2，则d(Tλ(x1),Tλ(x2))>δ. 因此，系统(X,{Tλ}λΛ)是敏感的. 证毕.

3 有向部分半群作用的n-敏感

本节研究有向部分半群作用下紧致度量空间上的Λ-拓扑动力系统的n-敏感性，得到了n-敏感的一些性质并且给出了敏感性和n-敏感性之间的关系．

Δn(ε)={(x1,…,xn)Xn:d(xi,xj)<ε,∀1≤i≤j≤n}.

显然点(x1,…,xn)Qn(X,T)当且仅当对于任意ε>0和xi的任意邻域Ui，存在Ui和λΛ,有d(TλTλ下面给出Q-集的定义．

定义14设集合S⊆X. 如果对任意n≥2，(x1,…,xn)Qn(X,T)，有(x1,…,xn)Sn，则称S是Q-集.

对于点(x1,…,xn)Xn，定义集合L(x1,…,xn)如下：xL(x1,…,xn)当且仅当对xi的任意邻域Ui及x的任意邻域U，存在U,使得TλUi(1≤i≤n)．

性质8设(Λ,,*)是有向部分半群，(X,{Tλ}λΛ)是一个可交换的Λ-拓扑动力系统，是(Λ,,*)上的适配余理想基，且对任意λΛ，集合{iΛ:i*λ}⊂Λ． 设B,如果X具有稠密的B-传递点集且yTransB(X)，则以下结论成立：

(1)L(x1,…,xn)是闭集.

(2)L(x1,…,xn)非空当且仅当(x1,…,xn)Qn(X,T)． 如果yL(x1,…,xn)，且对于任意λΛ，L(x1,…,xn)是Tλ-不变的，那么L(x1,…,xn)=X．

证明结论(1)是显然成立的，下面证明结论(2). 假设L(x1,…,xn)非空且令xL(x1,…,xn)． 由于集合

Wn={(Tλ1y,…,Tλny):yTransB(X),λ1,…,λnΛ}

在Xn中稠密，且Wn中的每个元素都是B-回复的，则B-回复集也在Xn中稠密. 设U是x的邻域，Ui是xi的邻域，则存在λΛ和U,使得对任意1≤i≤n，有TλUi． 不失一般性，假设是B-传递点，则存在λ′≻λ，使得Tλ′(TλU(1≤i≤n)． 因此，(x1,…,xn)Qn(X,T)．

另一方面，假设(x1,…,xn)Qn(X,T)．设是xi的邻域且满足其中kΛ且1≤i≤n． 对任意k，存在λkΛ和有由紧致性，对任意i，可假设由于Wn是Xn的稠密集，不难得到xL(x1,…,xn). 证毕.

下面给出相对于集合K敏感的Λ-拓扑动力系统的定义.

定义15设X是紧致度量空间，(Λ,,*)是有向部分半群，(X,{Tλ}λΛ)是Λ-拓扑动力系统． 设K是X的子集且Card(K)≥2，如果对任意(x1,…,xn)KnΔn，均有L(x1,…,xn)=X成立，即对点xi的任意邻域Ui、任意xX和x的邻域U，存在λΛ和U，使得对任意的i(1≤i≤n)，有TλUi，则称系统(X,{Tλ}λΛ)是相对于集合K敏感的. 这样的集合K叫做初值敏感集或者S-集．

对任意n≥2，记Sn(X,T)={(x1,…,xn):(x1,…,xn)Δn且{x1,…,xn}S}.

以下定理给出了在有向部分半群作用下,Λ-拓扑动力系统中的S-集和Q-集之间的关系.

定理2设(Λ,,*)是有向部分半群，(X,{Tλ}λΛ)是一个可交换的Λ-拓扑动力系统，是(Λ,,*)上的适配余理想基且对任意λΛ，集合{iΛ:i*λ}⊂Λ. 设B，且对于任意(x1,…,xn)Xn，对任意λΛ，集合L(x1,…,xn)都是Tλ-不变的. 如果X中包含稠密的B-传递点集，那么任意S-集都是Q-集；当(X,{Tλ}λΛ)是极小系统时，逆命题成立．

证明假设X包含稠密的B-传递点集，集合A是S-集且(x1,…,xn)Sn(X,T)∩An． 设xX且对任意自然数k≥1，Uk是x的非空开邻域且满足diam(Uk)<1/k． 设Vi是xi的邻域，则对任意k≥1，存在λkΛ及Uk，使得Vi. 由假设易知B-回复点集在Xn中稠密，不妨设是Xn的B-回复点，则存在λ≻λk，使得TλUk． 这就意味着(x1,…,xn)Qn(X,T)．

下面假设(X,{Tλ}λΛ)是极小系统． 设A是一个Q集且(x1,…,xn)AnΔ(n)，对任意k≥1和xi的任意邻域Ui，存在Ui和λkΛ，使得

下面给出n-敏感的Λ-拓扑动力系统的定义.

定义16对给定的自然数n≥2，称系统(X,{Tλ}λΛ)是n-敏感的，如果存在ε>0，使得对任意非空开集U，存在两两互异点x1,x2,…,xnU及λΛ，使得min{d(Tλxi,Tλxj):1≤i≠j≤n}≥ε．

由定义16，易得以下结论.

定理3设(Λ,,*)是有向部分半群，(X,{Tλ}λΛ)是一个可交换的Λ-拓扑动力系统，是(Λ,,*)上的适配余理想基且对任意λΛ，集合{iΛ:i*λ}⊂Λ. 设B，且对任意λΛ，L(x1,…,xn)是Tλ-不变的. 如果X包含稠密的B-传递点集且(X,{Tλ}λΛ)是n-敏感的，那么对任意n≥2，有Sn(X,T)Δn≠∅．

证明假设系统(X,{Tλ}λΛ)是n-敏感的． 设x是B-传递点,对任意的m+，设Um是x的开邻域且diam(Um)<1/m，则存在常数ε>0，使得对任意自然数m，存在B-回复点Um×…×Um及λmΛ，当i≠j时，有不失一般性，假设显然x1,…,xn是两两不同的,且xL(x1,…,xn)． 因此,L(x1,…,xn)=X，即(x1,…,xn)Sn(X,T)． 证毕.

接下来证明对于紧致度量空间上的Λ-拓扑动力系统来说，在X是局部连通空间的条件下，敏感性与n-敏感相互等价．

定理4设(Λ,,*)是有向部分半群，(X,{Tλ}λΛ)是一个Λ-拓扑动力系统且X是局部连通空间． 如果(X,{Tλ}λΛ)是敏感的，那么它也是n-敏感的(n≥2，n+)．

证明设ε是一个敏感常数，U是X的非空开集且n≥3． 由于X是局部连通空间，则存在非空连通开子集W⊂U． 由于X是敏感的，则可选取x,yW及λΛ，使得d′=d(Tλ(x),Tλ(y))>ε．

对于选出的这个λ，定义f:Tλ(U)→，使得f(z)=d(Tλ(x),z). 易知f是连续的． 由于Tλ(U)是连通的且f(Tλ(x))=0,f(Tλ(y))=d′，可得f(Tλ(U))⊃[0,d′]. 选取n个互异点λTλ(y)Tλ(U)，使得对任意i=1,2,…,n,有选取x1=x,x2,…,xn-1,xn=yU，使得

这就证明了系统(X,{Tλ}λΛ)是n-敏感的． 证毕.

由定理4，易得以下推论：

推论1设(Λ,,*)是有向部分半群，(X,{Tλ}λΛ)是一个Λ-拓扑动力系统且X是局部连通空间． 那么对于任意自然数n≥2，系统(X,{Tλ}λΛ)是敏感的当且仅当它是n-敏感的．