基于单自由度扭转模型的空调定速涡旋压缩机启动力矩识别
陶友淘 尹崇达 杜明龙
青岛海信日立空调系统有限公司 山东青岛 266000
1 引言
随着人们对环境舒适度要求的提高,空调的装机量越来越大,因此对空调的可靠性提出了更高的要求。对于采用定速压缩机的空调,压缩机启动时产生的配管应力是衡量空调可靠性的重要因素。配管启动应力由压缩机启动力矩和压缩机-配管系统动力学特性决定,压缩机启动力矩的精确计算是预报配管启动应力的基础。
为降低定速压缩机启停时配管应力,相关学者进行了大量研究。倪申[1]等通过对压缩机单相电机建立模型,计算出电机启动时的力矩,并通过单自由度模型计算冲击载荷下的系统响应。钱兴华[2]基于压缩机工作腔压力循环过程计算了容积式压缩机的启动力矩。曹兴枫[3]等以压缩机启动最大转角为目标,将瞬态启动力矩简化为静态启动力矩,并基于虚拟样机技术计算启动力矩。吕千浩[4]分析了压缩机脚垫硬度对空调管路应力的影响。张文锋[5]根据压缩机启动、停机、运行时实测加速度数据及模态分析,提出了配管优化方法。刘艳涛[6]基于仿真模型计算了压缩机启停过程中的配管应力。但是这些关于压缩机启动的研究,均存在一定程度的简化,不能得到真实的启动力矩。
为了得到准确的压缩机瞬态启动力矩,本文提出了一种基于模态测试的压缩机扭转角加速度传递函数计算方法,并建立单自由度扭转模型。最后根据杜哈梅积分与载荷函数法[7]识别压缩机启动力矩。
2 压缩机启动测试
2.1 启动应力测试
压缩机启动瞬间,压缩机内部转子系统克服惯性产生的载荷通过压缩机外壳传递到配管系统上,在配管上产生较大的启动应力。因此,为保证配管在压缩机多次启动后不发生断裂,我司在研发定速涡旋压缩机的室外机时,需要测试涡旋压缩机启动时配管测点处的应力,通常在配管焊点与配管折弯处。图1为某涡旋压缩机应力测点及压缩机启动瞬间的应力曲线。
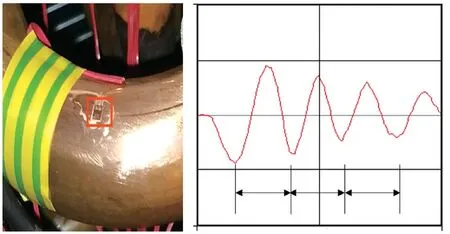
图1 应力测点及应力曲线
从应力曲线可以看出:(1)应力曲线具有明显的周期性,频率大约30 Hz;(2)应力幅值先增大后减小,在第二个波峰处达到最大。因此,可以推测定速压缩机启动时产生冲击载荷,并且压缩机与配管组成的系统的某一模态起主要作用。
2.2 壳体加速度测试
配管、压缩机橡胶底脚、压缩机本体组成一个结构动力学系统。但是相对于配管、压缩机橡胶底脚而言,压缩机可以看作刚体,因此压缩机可能存在6个方向的运动。为识别出涡旋压缩机启动瞬间的运动方向,在涡旋压缩机壳体上布置两个3向加速度测点,如图2所示。

图2 加速度测点
压缩机启动瞬间的加速度响应,如图3所示。

图3 涡旋压缩机启动瞬间测点加速度
涡旋压缩机启动瞬间,通过壳体上的两个测点的加速度曲线可以看出:(1)切向加速度远大于法向加速度与垂向加速度;(2)两个测点的切向加速度大小相等,方向相同,如图4箭头所示;(3)在涡旋压缩机启动的第一个周期内,切向加速度波动较大,从第二个周期开始呈现明显的周期性,且频率大约30 Hz。
根据以上三点现象可以看出,启动瞬间涡旋压缩机主要为扭转运动,进一步可以推断出涡旋压缩机启动载荷为绕垂直方向的力矩,如图4所示。
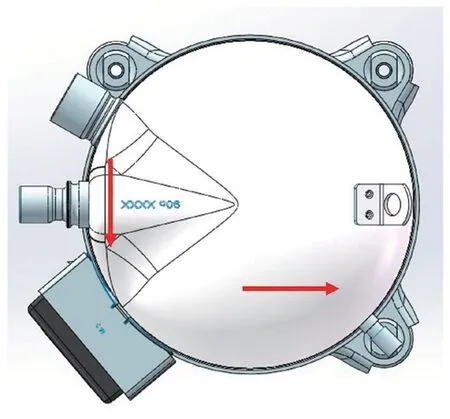
图4 涡旋压缩机启动瞬间运动方向
2.3 压缩机模态测试
为进一步探究启动应力与压缩机扭转运动的关系,对压缩机进行模态测试。在2.2节已经确定压缩机启动载荷为绕垂直方向的力矩。因此,为更好的激励起压缩机扭转模态,将力锤敲击点选在远离压缩机中心的位置,如图5所示。

图5 压缩机模态测试
根据以上测试方法,得到两个测点的切向加速度响应如图6所示。
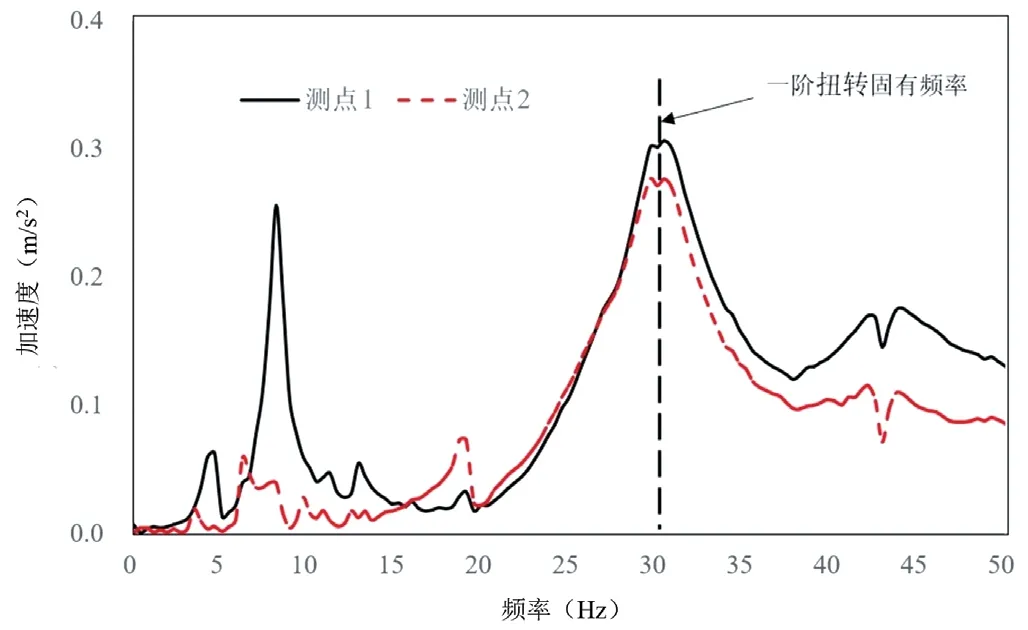
图6 测点切向加速度响应
根据切向加速度曲线可以发现,该空调外机的涡旋压缩机一阶扭转模态为30 Hz。
结合启动应力曲线、压缩机切向加速度曲线和压缩机切向加速度传递函数可以得出结论,启动应力与涡旋压缩机一阶扭转模态直接相关。
3 压缩机启动力矩识别方法
根据以上分析,启动应力与涡旋压缩机一阶扭转模态直接相关,因此可以将复杂的涡旋压缩机模型简化为单自由度扭转模型,用于压缩机启动力矩识别。
3.1 单自由度扭转模型
建立压缩机扭转自由度坐标系,如图7所示。

图7 压缩机扭转自由度坐标系
压缩机扭转自由度运动方程:

式(1)中,JR为转动惯量;cR为扭转阻尼;kR为扭转刚度;M(t)为启动力矩;为角加速度;为角速度;θ为角度;无阻尼固有频率;阻尼比 ;有阻尼固有频率
压缩机角加速度通过压缩机壳体的加速度计算得到:

式(2)中,为压缩机壳体加速度时域曲线;r为壳体测点与压缩机中心之间的距离。角速度、角度θt通过角加速度 积分得到。
3.2 扭转传递函数测试
不同于力到测点的传递函数,力矩到测点的传递函数难以测试。压缩机本身刚度较大,相对于配管而言,压缩机可以视为刚体。因此,可以采用敲击压缩机不同位置的方法计算出压缩机扭转力矩到测点的传递函数,如图8所示。
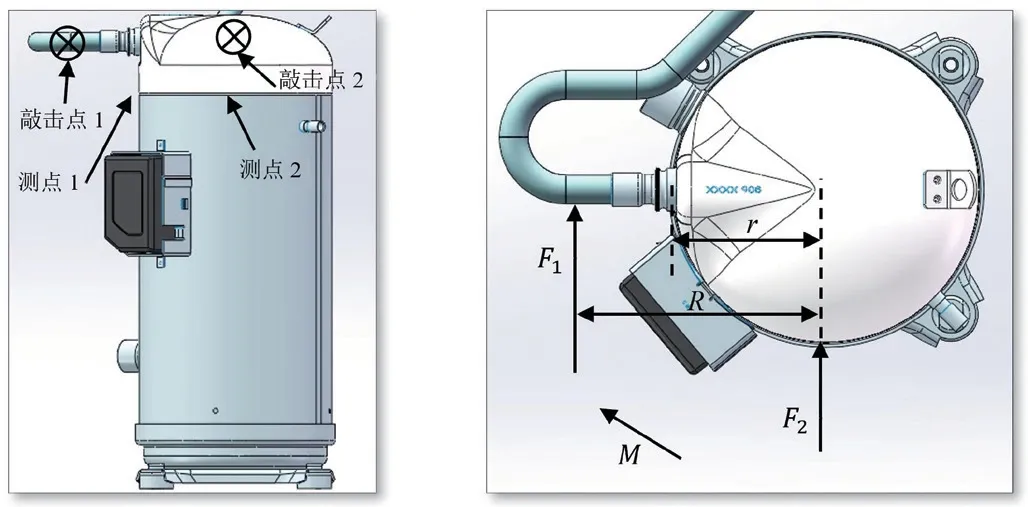
图8 压缩机敲击点与测点
以压缩机中心为轴,可以将敲击点1的敲击力F1分解为:(1)绕中心轴的力矩M;(2)平行F1且穿过压缩机中心的力F2。因此,压缩机扭转力矩到压缩机切向加速度传递函数可以通过敲击点1与敲击点2的测试结果得到:

式(3)中, 为敲击点1到测点1的加速度传递函数; 为敲击点2到测点1的加速度传递函数;R为敲击点1到压缩机中心的垂向距离,如图8所示。
进一步,压缩机扭转传递函数为:

根据敲击点1与敲击点2的模态测试数据,结合式(3)与式(4),得到压缩机扭转响应如图9所示。
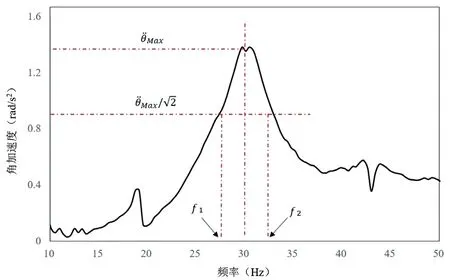
图9 扭转力矩响应

扭转刚度:

转动惯量:

根据式(5)(6)(7)可以计算出式(1)中的JR、cR、kR。
3.3 启动力矩计算方法[7]
根据3.1与3.2节介绍的内容,式(1)中只有M(t)是未知的,本文采用单自由度动态载荷识别方法计算M(t)。
首先,根据杜哈梅积分,式(1)角度、角速度、角加速度为:
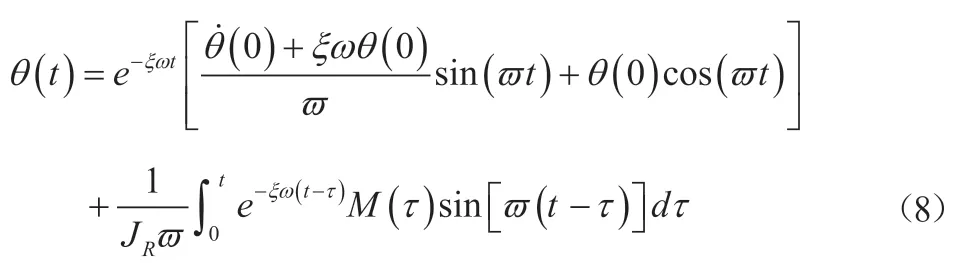
其次,假设M(t)在3个连续时刻内,满足载荷函数M(t)=at2+bt+c,如图10所示。将计算载荷的问题转化为求每个时刻载荷函数M(ti)对应的ai、bi、ci。

图10 载荷函数
最后,构建误差函数计算启动力矩M(t)。
4 压缩机启动力矩计算实例
某压缩机启动测试,在压缩机壳体上布置2个加速度传感器如图11所示。

图11 压缩机壳体测点
测点1切向加速度曲线如图12所示。可以看出从压缩机启动,切向加速度只在0.1秒内较大,0.1秒后迅速衰减,因此只截取启动开始后0.1秒的加速度信号进行分析。该加速度信号第一个半周期数值较小,最大信号发生在第四个半周期内,且第二个半周期内有两个峰值。
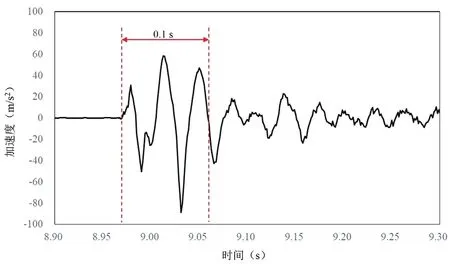
图12 切向加速度曲线
根据第3部分介绍的方法,计算出启动力矩如图13所示。
由图13可以看出,压缩机启动力矩并不是严格的正弦函数曲线。在第一个半周期内存在两个峰值,第一个较大,第二个较小。第二个半周期,启动力矩较为光滑。且经过两个半周期后,启动力矩迅速衰减。
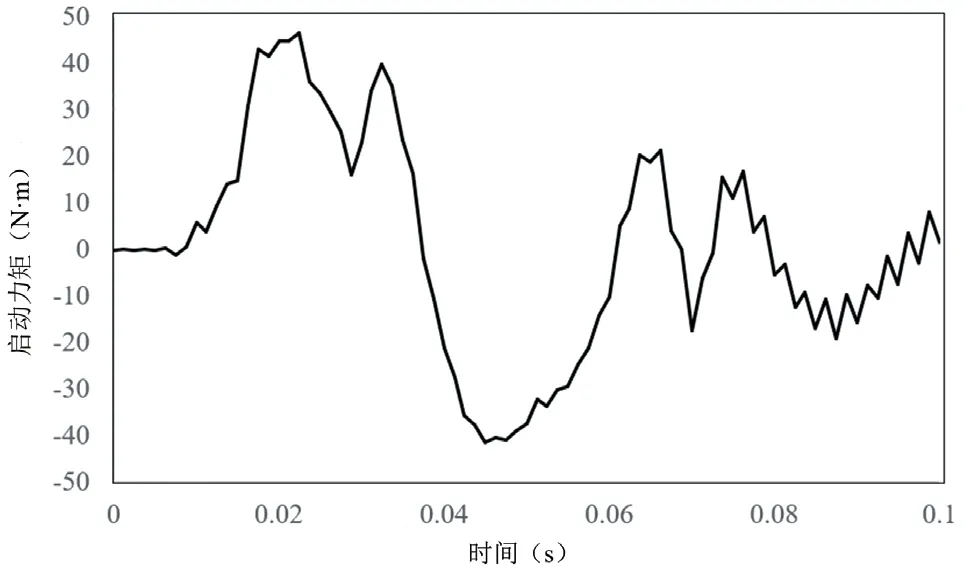
图13 压缩机启动力矩
将计算出的压缩机启动力矩加载到仿真模型中,压缩机切向加速度如图14所示。

图14 压缩机切向加速度实测与仿真对比
由图14可以看出整体上仿真结果与实测结果一致性较好,满足工程应用。第一、二个半周期几乎完全重合,加速度最大时误差最大,约20%。
5 结论
本文基于某空调外机定速涡旋压缩机启动加速度测试数据,发现涡旋压缩机启动瞬间主要绕垂直方向做扭转运动,且衰减频率与涡旋压缩机一阶扭转固有频率一致。并将识别出的启动力矩加载到仿真模型,得到的压缩机壳体加速度与实测加速度一致,为后续优化配管应力提供了有力工具。

