挤压型材压制成形回弹预测与补偿研究
董恒玮,蔡成,门向南,杨坪川,王磊
挤压型材压制成形回弹预测与补偿研究
董恒玮1,蔡成2,门向南2,杨坪川2,王磊2
(1.空装驻成都地区第一军事代表室,四川 成都 610091;2.航空工业成都飞机工业(集团)有限责任公司 钣钳加工厂,四川 成都 610091)
航空挤压型材的压制成形工艺是一种重要的飞机钣金成形工艺方法,由于压制成形过程存在回弹现象,科学准确地预测回弹补偿值对于提高产品质量具有重要的意义。为了有效预测航空挤压型材压制成形工艺过程产生的回弹,利用ABAQUS软件建立了一种挤压型材零件压制成形工艺过程的有限元仿真建模方法,利用预定义场模型研究了成形过程的回弹仿真技术并通过工艺试验进行了验证。该方法对于其他种类的航空钣金零件的成形仿真及回弹预测研究也具有积极的参考意义。
ABAQUS;挤压型材;压制成形;有限元方法
现场生产过程中挤压型材的压制成形工艺(闸压与液压成形工艺)都存在回弹现象。由于工艺模型补偿回弹仅凭工艺人员经验,导致某些情况下试模出现不合格现象,成形后需依靠手工校正。随着产品研制向多样化、快速化方向发展,传统凭借经验的工艺模式逐渐显现出试制产品质量不稳定、周期不可控等问题。谭学明等[1]提出一种基于有限元计算的平整性修模与下陷深度修模结合的模具型面迭代修正算法;韩志仁等[2]利用有限元方法模拟型材下陷成形过程,预测了型材下陷回弹补偿量;熊旭等[3]针对型材热压下陷成形缺陷分析及抑制方法进行研究,建立不同模具方案下的型材下陷成形有限元模型,并进行了有限元模拟。同时,长期以来的工艺系统积累了一定的关于型材类零件压制成形的模具设计知识及回弹补偿经验知识。现场试模合格后稳定投产的零件也为开展相关数字化研究提供了丰富案例,可用于有限元模型的修正与优化。
综合现有工作基础与优势,将长期以来积累的工艺经验与数字化分析方法相结合,促进技术转型升级,对于提高零件的成形质量与生产效率具有积极的现实意义。
1 材料塑性成形力学参数测试
研究分析典型的挤压型材材料屈服应力、抗拉强度、弹性模量及应力-应变关系等,建立企业的典型挤压型材材料物性参数数据库,为有限元仿真提供物性参数依据。
通过材料的单向拉伸试验可以获得有限元仿真所需的材料物性参数数据。选取某项目中牌号7050-O的铝合金挤压型材作为典型分析对象进行试验,实验完成后的试片如图1所示,其真实应力-塑性应变曲线关系如图2所示。
2 有限元建模与实验分析
型材的压制成形工艺(闸压与液压成形工艺)是一种重要的钣金成形工艺,是在压力设备(闸压机或单柱/多柱液压机)上使用压模(压制成形模具)通过模具上模与下模之间的压力压制成形零件几何外形的一种成形工艺方法。
型材压制成形是典型的非线性问题:金属材料进入塑性成形阶段是典型的材料非线性问题;原材料形状发生改变,由原材料状态变为零件状态,是典型的几何非线性问题;上模与下模和零件接触状态发生变化,由不接触/局部接触变为接触,是典型的接触非线性问题[4-5]。

图1 单向拉伸试验完成后试片的示意图
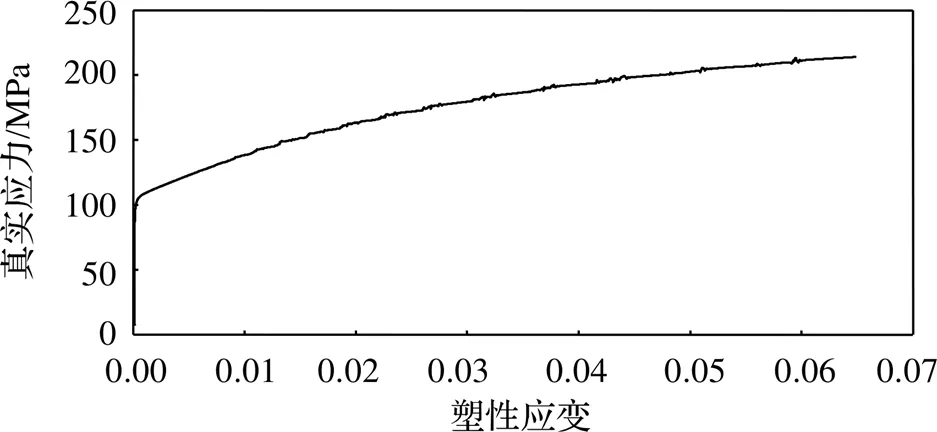
图2 7050-O挤压型材材料的真实应力-塑性应变曲线
采用ABAQUS软件建立有限元分析模型,利用数值模拟方法对成形过程进行仿真是一种广泛使用的方法[6]。以某Z字形截面型材零件为例,建立其压制成形零件的有限元分析模型,计算成形后的变形回弹值。零件模型如图3所示,零件的材料牌号为7050-O。
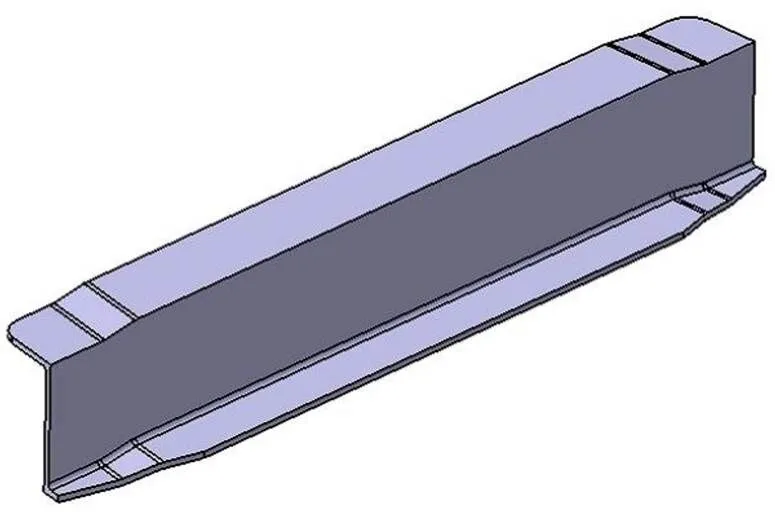
图3 典型Z字形型材零件示意图
2.1 几何模型的创建
利用CATIA软件绘制型材压制成形的几何模型。为减小计算量,该零件某单个下陷如图4所示,其利用挤压型材原材料压制成形下陷后铣切外形制造,下陷深度2.0 mm,下陷过渡区长度14.3 mm,零件两边宽分别为25 mm及19 mm,材料厚度2 mm,立边高度41 mm,属于典型的挤压型材压制成形类零件。

图4 某Z字形型材压制成形零件示意图(压制后铣切前)
利用CATIA提取曲面的功能,提取该零件的两个表面模拟成形过程中的模具表面,提取后移动表面,使两面的几何位置关系为上模与下模的初始位置。针对图4所示零件,提取零件的下表面作为下模的模具表面后保持几何位置不变,提取零件的上表面作为上模的模具表面后沿下陷成形方向的反方向将上模表面移动2 mm作为上模的初始位置,其中2 mm即为零件的下陷深度值。根据零件的几何外形绘制压制成形前原材料的几何模型。通过装配功能导入绘制的三个模型,导入后几何关系如图5。

图5 某Z字形型材压制成形几何关系示意图
将CATIA中绘制的上模、下模及原材料的几何模型另存为IGS格式,依次导入ABAQUS软件。将原材料几何模型作为部件导入,定义其模型空间为“三维”,类型为“可变形”;将上模和下模的几何模型作为部件分别导入,定义模型空间为“三维”,类型为“离散刚体”。
2.2 创建材料属性及分析步
选择属性模块,创建7050-O材料属性。定义:密度分布一致,质量密度2.81×10-9kg/mm3;弹性为各向同性,杨氏弹性模量72670 MPa,泊松比为0.33;塑性硬化为各向同性;屈服应力112.1 MPa;抗拉强度220.4 MPa,断面收缩率26.6%;延伸率15.0%;塑性应变参数由材料单向拉伸试验获取,如表1所示。

表1 材料参数数据表
选择分析步模块,在初始分析步后创建成形过程的分析步,分析步的类型定义为“动力显式”,采用动态显式算法分析压制成形过程。应用动态显式算法计算塑性成形过程具有计算效率高、处理接触问题相对准确等优点[7]。
2.3 创建相互作用
选择相互作用模块,建立毛料与压模之间的接触关系。选择创建相互作用属性子模块,创建铝-钢的相互作用属性,并定义属性的切向行为和法向行为。定义切向行为的摩擦公式为Penalty Algorithms,并定义摩擦系数为0.1,方向性为各向同性;定义法向行为为压力过盈硬接触,同时允许接触后分离。
创建上模与毛料之间的接触,选择接触类型为表面与表面接触(Explicit),并选择主面为上模与毛料接触的面,选择从面为毛料与上模接触的面,选择力学约束公式为运动接触法,选择滑移公式为有限滑移,选择接触作用属性为本节中创建的铝-钢相互作用,选择约束在初始分析步中创建,并传递至成形分析步。采用相同的方法创建下模与毛料间的接触关系。建模过程中始终选择刚度较大的面作为主面,选择刚度较小的面作为从面。
2.4 创建网格
选择网格模块,对部件毛料、上模及下模划分网格。Z字形截面的挤压型材由于截面较为复杂、无法直接使用结构化的网格划分方法进行网格划分,需要合理地对结构进行拆分,确保拆分出的子结构能够使用结构化的网格划分,为实现此目的,按照图6中标识的边界对毛料进行分割操作。
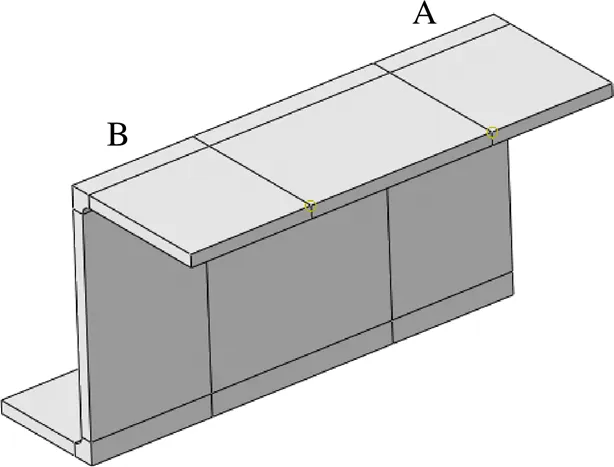
图6 结构化划分型材示意图
选择网格控制属性子模块,选择单元形状为六面体单元,选择使用结构网格划分技术,最终选择的单元类型为C3D8R(八结点线性六面体单元,减缩积分并沙漏控制),选择单元施加的对象为毛料。
选择全局种子子模块,选择近似全局尺寸为2,并将全局种子应用于毛料。选择为边布种子模块,选择图7中用于分割的边,设置边的种子个数为5,提高相应部位的网格密度。划分后的网格如图7所示,模型完成网格划分后具有节点10656个和网格8400个。

图7 毛料网格划分结果示意图
2.5 定义载荷及边界条件
选择载荷模块,分析步定义为初始分析步,定义部件毛料的边界条件,选择图6中A区域的端面施加边界条件,选择分析步为初始分析步,选择约束条件类型为完全固定(U1=U2=U3=UR1=UR2=UR3=0),保持在初始及后续成形分析步中毛料A部分的端面不在空间中产生运动,该假设是对该零件压制成形过程的一种合理简化。
分析步定义为初始分析步,定义部件下模的边界条件,选择分析步为初始分析步,类别为力学,类型为对称/反对称/完全固定,选择边界条件的施加对象为刚体下模的参考点,选择约束条件的类型为完全固定(U1=U2=U3=UR1=UR2=UR3=0),保持下模在压制成形过程中固定。
分析步定义为初始分析步,定义部件上模的边界条件,选择分析步为初始分析步,类别为力学,类型为位移/转角,选择边界条件的施加对象为刚性上模的参考点,对于U1、U2、U3、UR1、UR2、UR3,在成形分析步中设置U3=-2.0(即压制成形方向移动2.0 mm),其余自由度设置为0。
2.6 分析计算
提交分析作业,计算结果如图8所示,压制成形过程中毛料的最大主应力为209 MPa、出现在下陷位置处Z字型型材的立边,该位置产生最大的变形抗力,也是回弹产生的最主要位置。成形分析过程中伪应变能与内能比值变化曲线如图9所示,比值小于10%可以认为模型为可靠模型。
2.7 回弹计算与实验分析
复制前述成形模型新建回弹的分析模型,在装配中删除上模及下模,仅保留零件的部件,删除原有的分析步和相互作用关系,取消成形分析步中设置的边界条件。在分析步管理器中定义回弹计算的分析步,设置类型为静力通用的隐式算法。隐式算法在处理多重非线性问题时效率较低且容易产生不收敛的现象,计算所耗费的迭代步数也较多,但可有效避免显式分析过程中的误差积累。隐式分析的每一个载荷步均能收敛,适合成形分析后的回弹计算[8]。即成形过程的分析计算选择显式算法、回弹分析过程采用隐式算法求解的组合具有最优的计算效率和计算精度[9-10]。

图8 回弹的应力云图
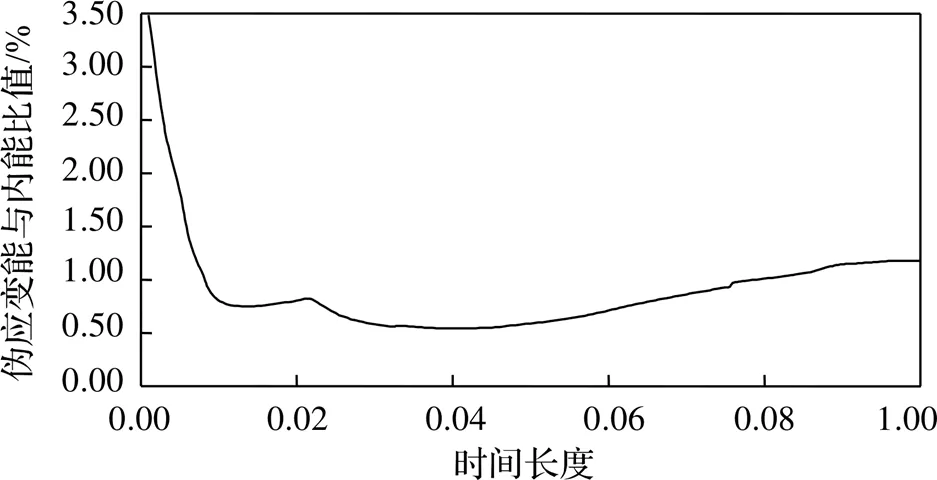
图9 伪应变能与内能比值关系示意图
在回弹分析模型中设置如图6所示的边界条件,其中A区域边界条件为完全固定(U1=U2=U3=UR1=UR2=UR3=0),B区域边界条件为位移/转角,并选择对下陷深度和长度方向自由度不进行约束,对其他自由度约束为0。
使用预定义场模型进行回弹计算,选择2.6节中成形计算的结果实例作为回弹计算模型的初始状态,其初始内部应力的分布如图8所示。创建回弹分析作业,并提交计算,回弹计算结果如图10所示。
按照回弹计算结果,模型中深度为2.0 mm的下陷回弹后的下陷深度为1.79 mm,该零件2.0 mm下陷的回弹为0.21 mm。按照该产品成形标准的要求,挤压型材下陷成形的公差为0~+0.2 mm,即下陷深度相比于理论深度仅能增加。将下陷加深0.4 mm,并利用该工艺数模设计制造压模,展开相关工艺实验,如图11所示,成形后的零件下陷深度为2.15 mm,符合公差要求。压制成形后零件下陷的回弹为0.25 mm,相比于工艺数模下陷加深后的下陷深度2.4 mm,其回弹的占比为10.4%。有限元分析模型中未加深的下陷深度为2.0 mm,其下陷回弹为0.21 mm,回弹占比为10.5%,实验验证了有限元模型的准确性。

图10 回弹的位移云图

图11 工艺试验结果示意图
针对现场常见的L字型、T字型与Z字型型材截面及LY12-M、2A12-O与7050-O三种常见的型材材料开展有限元仿真实验,实验针对下陷深度在2 mm以内、型材材料截面厚度在2.5 mm以内、立边高度在50 mm以内的常见型材零件展开。三种常见的型材材料的材料参数数据如表2所示。
按照上述建立的型材压制与回弹仿真建模方法,建立LY12-M、2A12-O与7050-O三种材料压制L字型截面型材零件的有限元分析模型,并进行回弹计算,计算结果如图12所示,零件下陷深度和材料厚度均为2 mm。
由有限元分析结果可知,LY12-M、2A12-O与7050-O三种常见的挤压型材材料,其中屈服强度较高而弹性模量较低的LY12M-M材料压制成形后具有更大的回弹。
按照上述型材压制与回弹仿真的建模方法,建立LY12-M材料针对L字型与Z字型型材截面的有限元分析模型,并进行回弹计算,其中L字型与Z字型截面的零件立边高度及材料厚度相同。L字型截面的计算结果如图12(a)所示,Z字型截面的计算结果如图13所示。可知,在立边高度相同、材料厚度相同、下陷尺寸相同的条件下,L字型截面相对Z字型截面的下陷成形后回弹更大,截面形状对于压制成形的回弹有影响,回弹随截面形状的复杂程度增大而减小。

表2 材料参数数据表

图12 不同材料计算L字型截面结果(成形与回弹)

图13 LY12-M材料计算Z字型截面结果(成形与回弹)
3 结束语
为了有效预测航空挤压型材压制成形工艺过程产生的回弹,通过对现场使用的材料的成形性能参数进行试验,获取挤压型材的屈服应力、抗拉强度、弹性模量及应力-应变等关系,建立了材料参数库,通过有限元仿真技术结合工艺试验研究建立并验证了一种典型挤压型材零件压制成形过程的有限元数值仿真建模方法,通过预定义场模型研究了成形过程的回弹仿真预测及其补偿修正技术。该方法能够较为准确地预测挤压型材压制成形工艺过程产生的回弹,对于其他种类的航空钣金零件的成形仿真及回弹预测研究也具有积极的参考意义。
[1]谭学明,吴建军,张深,等. 型材下陷成形回弹补偿算法[J]. 航空制造技术,2014(Z1):107-110,114.
[2]韩志仁,杜松宸,孟祥韬. 基于有限元分析与试验的型材下陷成形回弹[J]. 沈阳航空航天大学学报,2018,35(6):14-19.
[3]熊旭,何文华,徐莉萍,等. 型材热压下陷成形缺陷分析及抑制方法研究[J]. 机械与电子,2015(3):23-26.
[4]肖夏,刘雪垠. 三轴滚弯仿真有限元分析[J]. 机械,2017,44(3):18-21.
[5]杜松宸. 型材下陷加深方法与下陷成形模具快速设计[D]. 沈阳:沈阳航空航天大学,2019.
[6]张鸿羽,余敏,丁腾飞,等. 不同材质航空用沉头铆钉装配数值模拟[J]. 机械,2019,46(8):32-37.
[7]赵文涛,余峰,吴畏,等. 基于ANSYS的门机金属结构系统动态特性分析[J]. 机械,2018,45(4):27-31.
[8]刘静,杨合,詹梅,等. 铝合金管力学性能的拉伸试验研究[J]. 锻压技术,2010,35(2):113-116.
[9]刘春阳,赵晓男,陈光雄,等. 一系悬挂与扣件参数对钢轨波磨的影响分析[J]. 机械,2018,45(10):11-15,19.
[10]魏棵榕,尹自强,刘强,等. 双锥静压轴承结构设计与FLUENT仿真分析[J]. 机械,2019,46(5):8-13,18.
Research on Rebound Prediction and Compensation of Extrusion Profile Press Forming
DONG Hengwei1,CAI Cheng2,MEN Xiangnan2,YANG Pingchuan2,WANG Lei2
( 1.The 1st Military Delegate Room of Air Force Equipment to Chengdu, Chengdu 610091, China; 2.Sheet Metal Manufacture Plant, Chengdu Aircraft Industrial (Group) Co., Ltd., AVIC, Chengdu 610091, China )
The press forming process of aviation extruded profiles is an important aircraft sheet metal forming process. Due to the rebound phenomenon in the pressforming process, scientifically and accurately predicting the rebound compensation value is of great significance for improving the product quality. In order to effectively predict the rebound generated by the press forming process of aviation extruded profiles, a finite element simulation modeling method for the press forming process of extruded profile parts is established. The rebound simulation technology of the press forming process is studied by using the predefined field model and verified by the process test. The method also has positive reference significance for the forming simulation and rebound prediction of other types of aviation sheet metal parts.
ABAQUS;extruded profiles;press forming;finite element method
TH164;TG37
A
10.3969/j.issn.1006-0316.2021.12.007
1006-0316 (2021) 12-0049-07
2021-03-08
董恒玮(1992-),男,山东聊城人,助理工程师,主要研究方向为先进航空制造技术;蔡成(1991-),男,四川德阳人,工学硕士,工程师,主要研究方向为航空钣金制造技术;门向南(1983-),男,吉林榆树人,工学硕士,高级工程师,主要研究方向为航空钣金制造技术;杨坪川(1985-),男,四川绵阳人,高级工程师,主要研究方向为航空钣金制造技术;王磊(1986-),男,四川成都人,工学硕士,工程师,主要研究方向为航空钣金制造技术。

