一种基于ABAQUS的火箭弹部段连接刚度模型修正方法研究
杨磊,郭治斌,尤春艳,杨元华,杨俊波
一种基于ABAQUS的火箭弹部段连接刚度模型修正方法研究
杨磊,郭治斌,尤春艳,杨元华,杨俊波
(四川航天系统工程研究所,四川 成都 610100)
火箭弹按照不同功用被设计成若干个部段,部段间通过各种结构形式连接,其连接部位的刚度下降会显著影响全弹的固有特性。本文以某型火箭弹为例,首先,通过全弹刚度试验获取弹体受载后的变形数据;其次,基于ABAQUS软件,采用刚度试验数据结合有限元数值分析的刚度模型修正方法,对火箭弹部段连接刚度进行迭代修正,使得弹体变形量的计算值逐步逼近试验值;最后,利用修正后的模型对火箭弹前六阶固有频率和振型进行分析,分析结果表明经刚度修正后的固有特性计算值更为接近试验实测值,从而验证了该方法在分析此类问题时的有效性。
连接刚度;ABAQUS;模型修正;固有特性
有控火箭弹通常由战斗部、仪器舱、火箭发动机及尾段等部段组成,多部段的设计有利于日常维护和安装生产,因此形成了若干部段间连接面。根据部段的载荷、结构形式、尺寸空间等因素,在连接处采用套接、盘式连接、螺纹连接等接头形式将各部段组装起来,形成完整的弹身。受接头形式、配合间隙及预紧力的影响,连接处的刚度与附近部段的刚度相比较,必然会发生明显的变化,图1[1]给出了连接面对全弹刚度的局部扰动情况。
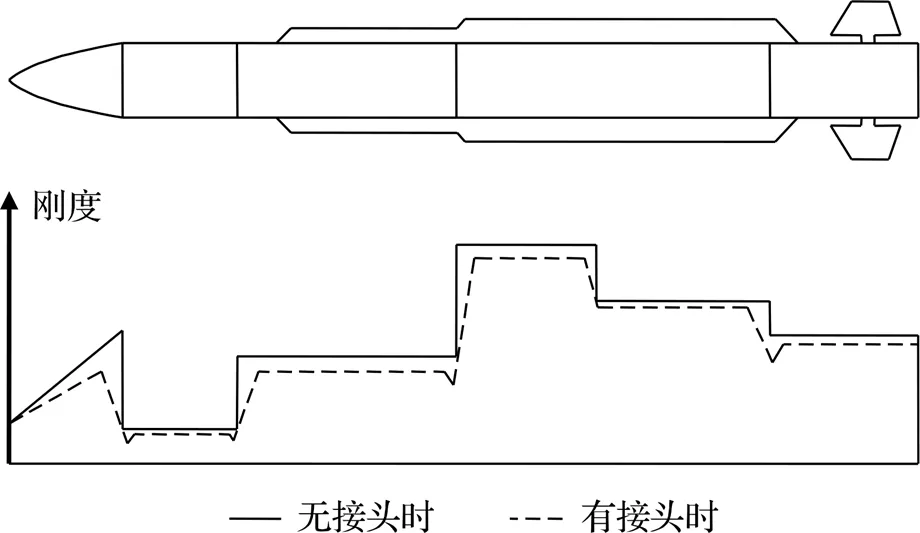
图1 连接面对全弹刚度的扰动
大量试验数据证明,根据接头数量、类型和位置的不同,刚度损失可达10%~40%,由于连接面削弱了相邻弹身的刚度,必将拉低大长细比火箭弹的固有频率,表1[2]中列举了一些导弹的一阶频率由于连接面的存在而引起的下降情况。
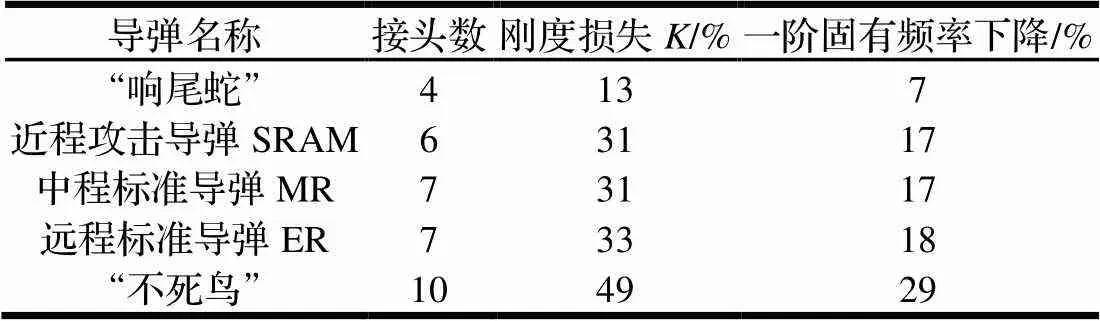
表1 连接面引起的刚度损失和频率下降
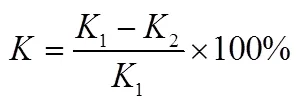
除此以外,连接面的存在同时改变了全弹刚度分布,必然使得振型形状、斜率、节点位置发生变化,这些模态参数是飞行姿态控制系统设计的依据。有控火箭弹的飞行控制原理[3],简单地说就是依靠陀螺和加速度传感器感受弹体刚体姿态和加速度,进而控制其飞行。然而当弹体沿垂直于纵轴方向振动时,陀螺感受的姿态中含有弹体弹性振动的附加姿态角,这一附加姿态角将导致火箭弹不能按设计轨道正常飞行。姿态控制系统设计中的一项重要任务就是根据模态参数设计出合理的滤波器将飞行过程中的附加干扰滤掉,确保火箭弹飞行姿态的稳定。因此,产品设计人员必须重视连接刚度对火箭弹系统设计的内在影响,及早掌握其变化规律。
有限单元法(Finite Element Method,FEM)自1943年提出并发展至今,已成为工程数值分析的有力工具[4-5],特别是随着电子计算机的广泛应用和发展,涌现了以ABAQUS、ANSYS为代表的一大批适用于工程领域的通用有限元软件,它们基于有限元理论,采用数值计算方法,拥有完备的功能模块和强大的前后处理能力[6],可以模拟庞大复杂的模型,处理高度非线性问题。应用任意一款通用有限元软件对部段本身的刚度进行分析均可得到非常准确的结果,但软件算法原理上都没有引入部段连接处的空隙、配合面表面粗糙度、接触状态等影响因素,使得很难直接对连接刚度进行有效预测。
随着火箭弹重量和结构尺寸的不断增加,弹体振动引起的姿态控制问题日益显著,连接刚度的研究得到了广泛关注。刘昌洪等[7]采用一种等效弹簧模型对导弹舱段连接接头进行简化,并应用这种模型分析了连接刚度对弹体固有特性的影响规律;郑晓亚等[8]将各被连接件和接头分开,建立不同粗细的网格模型进行计算,然后再将两种计算模型通过连接单元结合到一起,降低计算规模;何国军等[9]从盘式连接的接触有限元方法出发,计算出部段连接结构的抗压、抗剪、抗弯和抗扭刚度,采用三维模型描述导弹的整体特性,在部段分离面处用相应刚度的虚梁元来等效模拟连接刚度,分析全弹固有特性,取得了较好效果。
本文针对部段间连接刚度问题,首先通过全弹刚度试验获取弹体变形数据,然后基于ABAQUS建立部段及连接部位的三维有限元模型,并结合试验数据对连接处刚度进行修正,最后利用修正后的连接刚度对弹体固有特性进行分析对比,以此验证该修正方法的有效性。
1 刚度试验
全弹刚度试验的目的是通过测定弹体在外力作用下的变形或转角,获取弹体的刚度特性。本文对某型火箭弹进行刚度试验时,考虑到弹体长细比的值较大,火箭弹如果水平固定,则会因为自重变形引入附加变形量,给刚度数据带来偏差。为了消除重力的影响并保证所有部段间连接面均处于自由状态,将火箭弹竖直放置,在发动机结构上选取两个位置用于夹持固定全弹。将控制舱前端、尾段后端通过转接工装与多通道电液伺服加载系统连接,根据试验件的尺寸规模,分别在弹身两端加载2000 N单位载荷,试验方案如图2所示。
为了获取弹体结构在加载过程中的变形情况,尤其是部段间的连接刚度,在各部段连接面两侧布置位移测点,如图3所示。
试验时,为保证载荷平稳地施加到试验件上,以100 N为步长逐级加载到单位载荷,所有位移测量均待施加的载荷稳定后进行,弹身在单位载荷作用下的变形数据如图4所示。
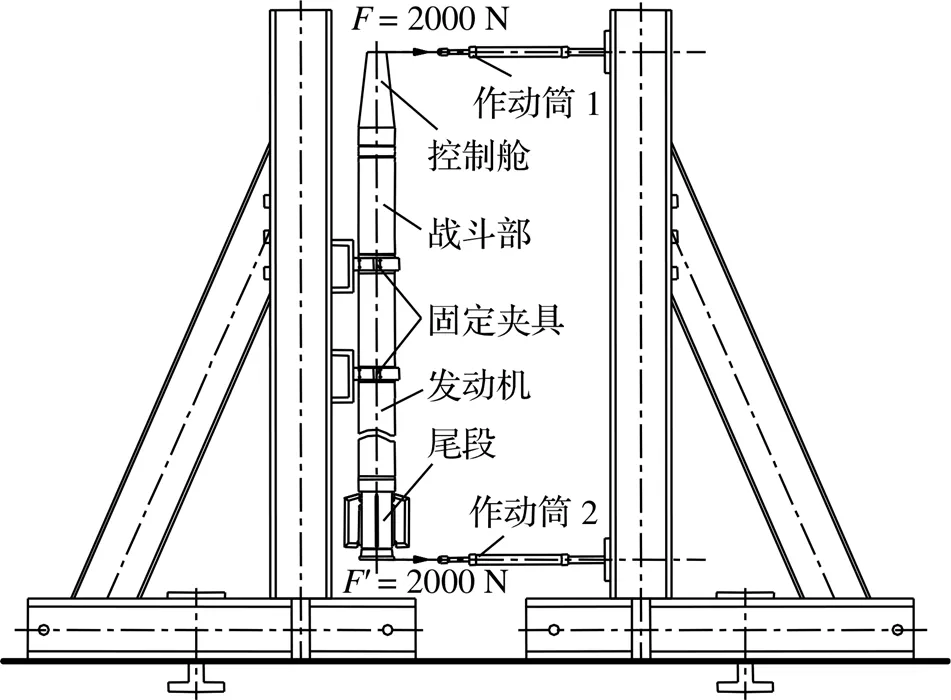
图2 全弹刚度试验方案
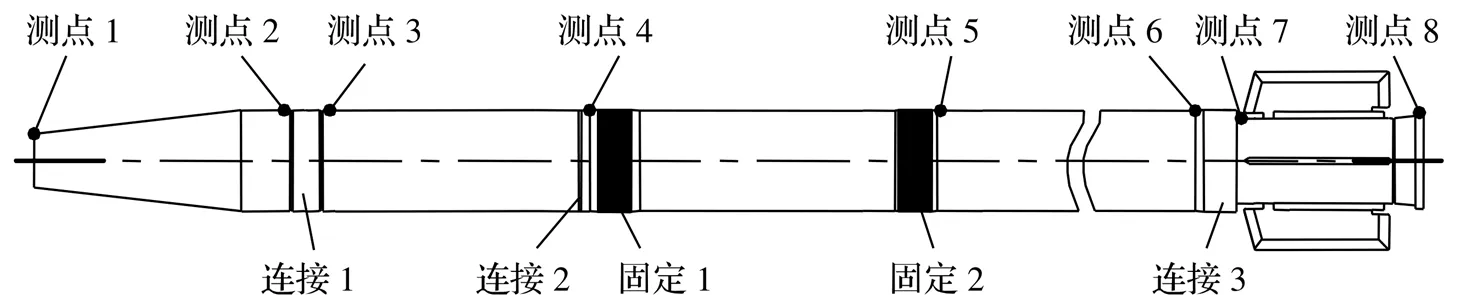
图3 刚度试验位移测点分布
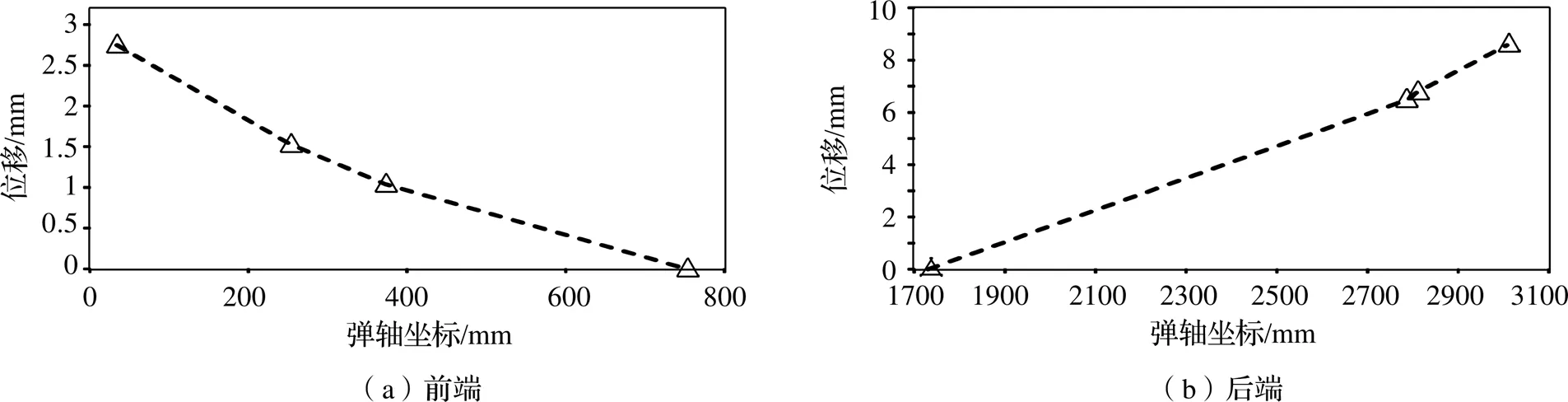
图4 弹身试验位移曲线
2 刚度修正方法
为简化计算,以往对全弹刚度进行分析时,通常忽略连接件,仅对各部段进行建模,然后将部段之间定义为固定连接。这种处理方式人为地提高了部段间的连接刚度,存在较大误差。基于ABAQUS的连接刚度修正方法则是根据刚度试验的位移结果来对刚度进行修正,以此获得更为准确的结果。该方法可以分为两个步骤:第一步,利用ABAQUS对全弹建立有限元模型,按试验状态进行约束和加载,得到全弹的位移数据;第二步,将上一步的计算结果与试验测得的变形数据进行对比、修正连接刚度,以此拟合位移曲线。
2.1 建立火箭弹有限元模型
参加刚度试验的某型火箭弹由控制舱、战斗部、发动机和尾段四个部段组成,除尾段材料为铝合金外,其余部段材料均为钢,其材料的性能参数如表2所示。利用Creo对各部段进行几何实体建模,建模过程中采取必要的简化,原则是不改变结构的基本几何特征、传力路线、刚度分配等。部段建模完成后,将部段按实际连接关系进行装配,然后采用ABAQUS与Creo之间专用接口程序导入几何模型。

表2 材料性能参数
2.2 划分网格
单元类型和网格的疏密程度直接影响运算时间及计算结果精确性,所以必须选择合理的单元类型及网格划分方法[10]。虽然采用线性完全积分单元的计算速度较快,但承受弯曲载荷时会出现剪切自锁,计算精度较差,不利于获得准确的变形结果。而非协调模式单元克服了剪切自锁问题,且在厚度方向上只需很少的单元就可得到与二次单元相当的结果,计算成本却明显降低,非常适合用于刚度分析,但使用时需确保网格没有大幅的扭曲,否则会大大降低精度。为确保网格规则,利用Partition Cell工具将各部段划分成为若干个简单区域,其中每个部段连接部位需单独划分为一个区域,以便对连接刚度进行修正,然后根据每个区域的特点生成结构网格或扫掠网格。经过对全弹进行网格划分,有限元模型中包含413224个节点和292920个单元,如图5所示。
2.3 定义作用关系
ABAQUS中常用的相互作用关系有接触(Contact)、粘接(Tie)、耦合(Coupling)、壳-实体耦合(Shell-to-Solid Coupling)等。按照本文采取的方法思路,不考虑部段之间的连接件,通过修正连接部位的刚度来调整变形量,因此将部段之间的作用关系定义为粘接;固定夹具的刚度远大于弹身,且与弹身之间为紧配合,将两者之间的作用关系也定义为粘接。
2.4 施加载荷与边界条件
在最终提交有限元静力分析前,还需对弹身施加载荷与边界条件,原则是力求与试验状态一致。在控制舱前端面和尾段后端面的所有节点上施加集中力(Concentrated force),即将单位载荷平均分配到各节点上,载荷方向垂直于弹身轴线;对固定夹具的底座设置固定约束(ENCASTRE)。完成了所有前处理步骤的全弹有限元模型如图6所示。
2.5 静力学求解
将全弹有限元模型提交求解器进行求解,全弹变形分布云图如图7所示。

图5 全弹有限元网格

图6 完成前处理的全弹有限元模型
从全弹变形结果中提取图3中各测点位置在单位载荷作用下的位移结果,弹身位移曲线如图8所示。通过对比计算与试验的位移数据可以发现,沿着弹身固定端到自由端的路径,在没有经过部段连接的弹身位移计算值与试验值较为一致(比如弹身后端从固定处到连接3之间),一旦经过三个部段间连接后位移计算值与试验值则出现较大的差异,并且连接部位越靠近固定端造成的影响越大(连接2造成的影响大于连接3),这说明对于部段本体的刚度计算已经非常准确,但因部段间连接刚度的误差导致弹身过于刚硬。
2.6 刚度修正
从图8位移曲线的趋势可以看出,因计算时部段间连接刚度偏大,造成弹身位移值偏小。按照刚度与变形成反比的思路,对各部段连接刚度进行修正,经过多轮反复迭代,位移计算曲线与试验曲线比较吻合,修正前后的连接刚度如表3所示,位移曲线如图9所示。
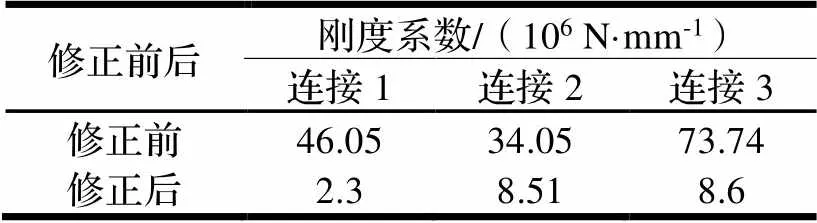
表3 修正前后连接刚度系数
3 固有特性分析
部段间连接面的存在使得连接刚度和阻尼发生非线性变化,从而导致结构固有特性的改变[11]。结构固有特性包括了结构的固有频率和振型,固有特性分析是动力学分析的基础,通过固有特性分析可以帮助设计人员确定火箭弹的固有频率和振型,从而进行姿态控制设计和仪器部件安装布局,避免发生频率耦合。

图7 全弹变形分布云图
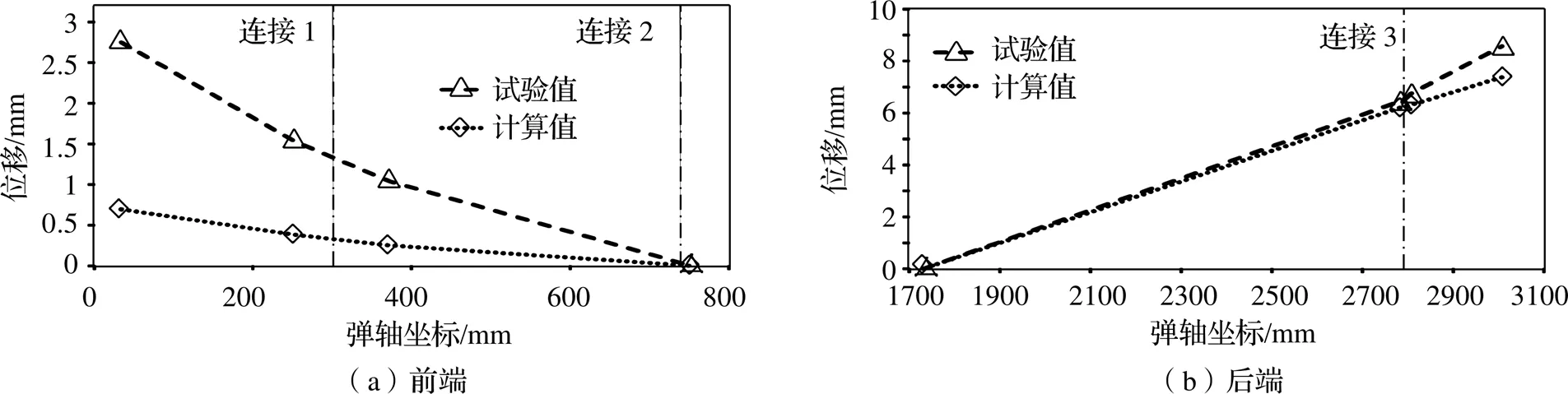
图8 弹身位移曲线
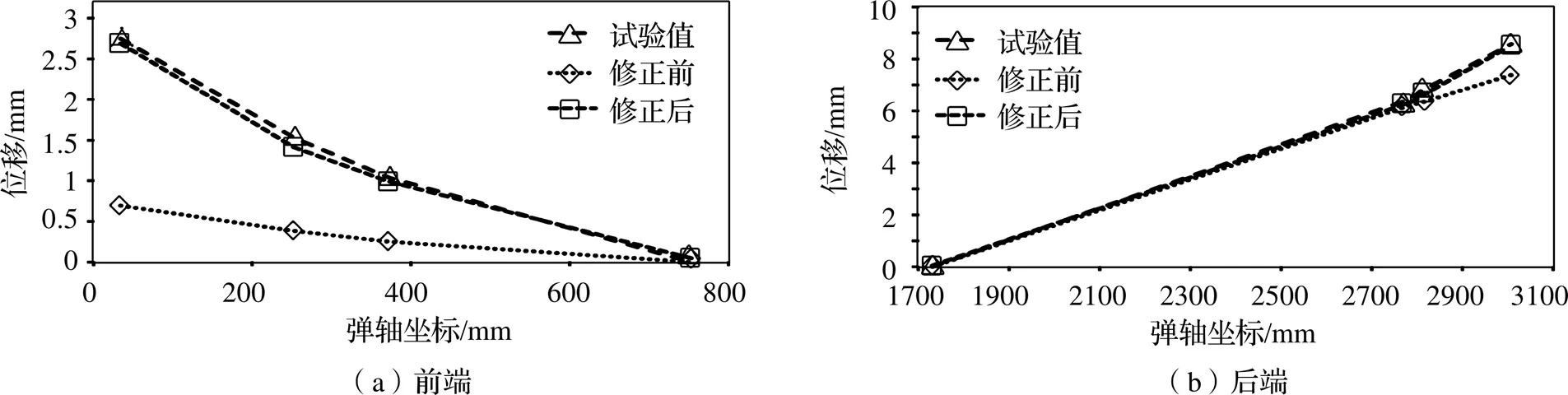
图9 弹身修正位移曲线
利用前面建立的有限元模型对全弹在自由状态下的固有特性进行分析,由于低阶模态对火箭弹的振动特性影响较大,所以选择前六阶的固有频率和振型进行研究。为了便于比较,分别计算连接刚度修正前后的全弹固有频率,结果如表4所示。
前六阶振型均为弯曲振型,典型振型如图10所示。
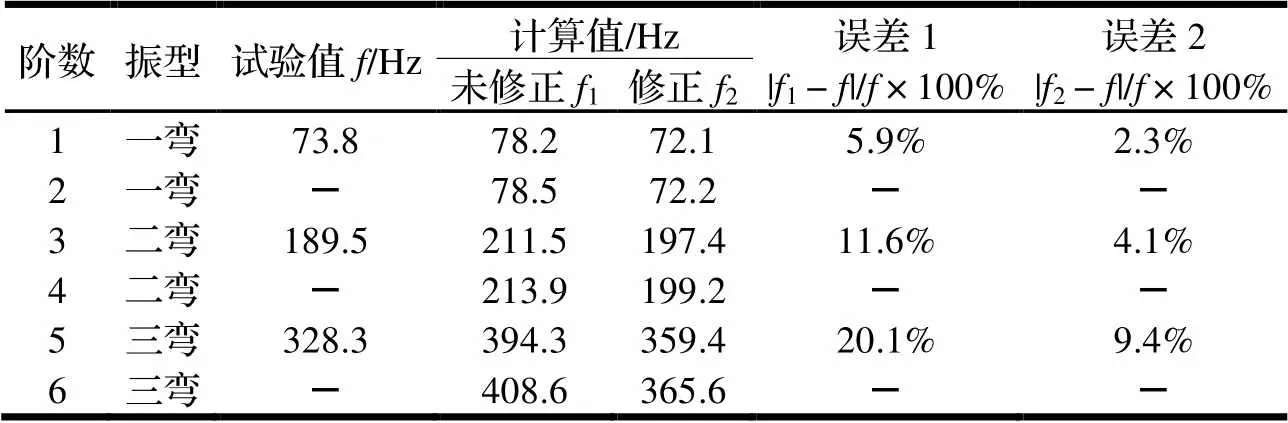
表4 固有频率计算结果
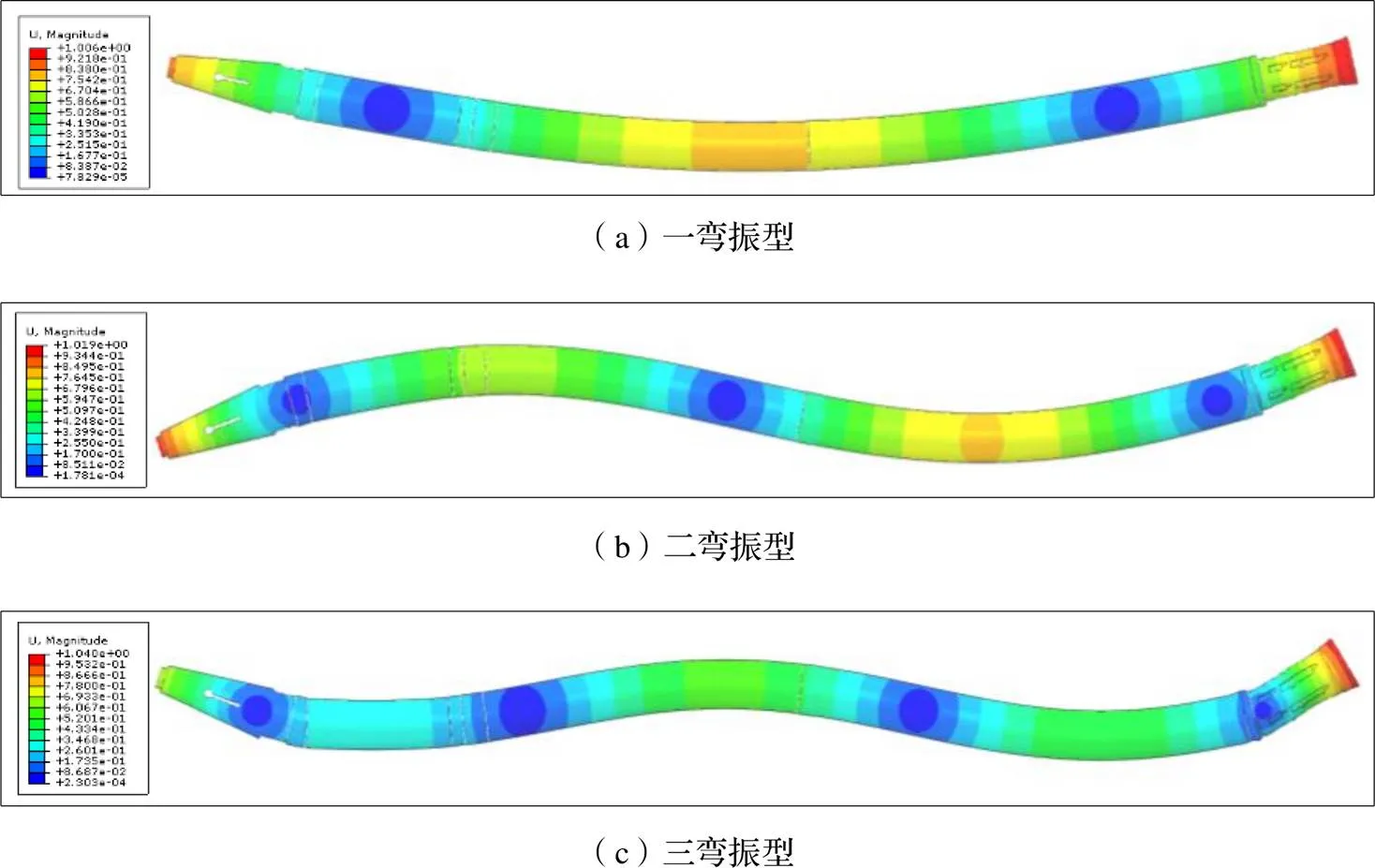
图10 典型振型
4 结论
本文根据全弹刚度试验数据,采用有限元软件ABAUQS对部段连接刚度进行了修正,进一步利用修正后的刚度参数对全弹固有特性进行了分析,其结果表明:
(1)部段之间的连接刚度与全弹刚度及固有频率成正比,随着连接刚度的降低,频率也随之降低;
(2)连接刚度对全弹固有特性的影响随着频率阶数的升高,表现得愈加明显;
(3)如果不考虑连接刚度的影响,就等于变相提高了全弹刚度,由此计算得到的固有频率与模态试验结果相比较,一弯、二弯、三弯振型对应频率的误差分别为5.9%、11.6%、20.1%,存在较大的偏差,因此在进行有限元计算时必须对连接刚度慎重考虑;
(4)在对连接刚度进行修正后,计算结果与试验相比,一弯、二弯、三弯振型对应频率的误差分别为2.3%、4.1%、9.4%,说明计算结果可信;
(5)由计算结果来看,根据刚度试验数据并采用ABAQUS对连接刚度进行修正的思路正确,对于连接面较多的火箭弹或者其他类似结构的仿真具有一定的工程实用价值。
[1]张延珍. 战术导弹连接刚度的研究[J]. 强度与环境,1992(2):28-34.
[2]余旭东,赵育善. 飞行器结构动力学[M]. 西安:西北工业大学出版社,1998.
[3]龙乐豪导弹与航天丛书——总体设计[M]. 北京:中国宇航出版社,2001.
[4]Courant R. Variational Method for Solutions of Problems of Equilibrium and Vibrations[J]. Bull. Am. Math. Soc.,1943(49):1-23.
[5]王勖成,邵敏. 有限单元法基本原理和数值方法[M]. 北京:清华大学出版社,1997.
[6]Chen Yuhmin,TsaoTienheng. A structured methodology for implementing engineering data management: an information model for cooperative product development[J]. Robotics and Computer- Integrated Manufacturing,1998,14(4):275-296.
[7]刘昌洪,成楚之. 战术导弹舱段联结刚度研究[J]. 现代防御技术,1997(3):24-32.
[8]郑晓亚,张铎,姜晋庆. 连接刚度对导弹固有特性的影响[J]. 弹箭与制导学报,2005(4):667- 669.
[9]何国军,竺润祥,尹云玉,等. 考虑连接刚度的导弹固有特性分析[J]. 强度与环境,2006(1):14- 17.
[10]石亦平,周玉蓉. ABAQUS有限元分析实例详解[M]. 北京:机械工业出版社,2006.
[11]王尚文. 航天器结构动力学[M]. 西安:西北工业大学出版社,1995.
Research on a Rocket Structure Connection Stiffness Model Updating Method Based on ABAQUS
YANG Lei,GUO Zhibin,YOU Chunyan,YANG Yuanhua,YANG Junbo
( System Engineering Institute of Sichuan Aerospace, Chengdu 610100, China )
The rocket consists of several structures according to different functions. And the structures have various forms of connections with different connection stiffness. The stiffness degradation of the connection significantly affects the inherent characteristics of the whole rocket. In this paper, a certain model of rocket is taken as an example. First of all, the deformation data of the rocket body after being loaded is obtained through the rocket’s structure connection stiffness test. Then, the stiffness model updating method based on the stiffness test data and the finite element analysis is adopted to iteratively correct the stiffness of the connection parts through the ABAQUS finite element software, so that the calculated value of the rocket body deformation gradually approximates the test value. Finally, the updated model is used to analyze the first six orders of the rocket’s natural frequencies and the mode shapes. The result shows that the calculated value of the inherent characteristics after the stiffness updating is closer to the test value, which verifies the validity of the method in analyzing such problems.
connection stiffness;ABAQUS;model updating;inherent property
TE415;TJ7
A
10.3969/j.issn.1006-0316.2021.12.006
1006-0316 (2021) 12-0043-07
2020-11-30
杨磊(1979-),男,重庆人,硕士,高级工程师,主要研究方向为力学仿真与试验,E-mail:leiyangcqu@163.com。

