基于粒子群算法的生产过程对象建模

周 斌， 陈 晶， 郑安豫， 张雅雯， 孟 尧

(安徽电气工程职业技术学院，安徽 合肥 230051)

为了设计性能优越的控制系统,一个前提条件是能充分的认识被控对象及系统内一切设备的运行规律,这种运行规律用数学语言表达出来就是我们常说的数学建模。目前,常用的建模方法有两大类,一类是根据被制对象的物理、化学定律建模,称为理论建模;一类是对一个具体的系统人为加入一个已知的输入信号,观察其输出,对比输入输出的信号,估计出其数学表达式的结构和参数,称为试验建模。这两类方法前者适合于对被控对象或系统有全面清楚的认知,能用成熟的理论进行描述,例如机械系统、力学系统及电气系统。但对于像电力或化工等生产过程而言建立的数学模型精度不够,不能应用于实际的工程,第二类试验建模则是一种较好的建模方法。近年来,智能控制算法在国内外有了飞速发展,已经进入工程化阶段,本文基于粒子群算法辨识生产过程对象的模型,过程简单方便,结果精度较好,可以接受。

1 建模过程

1.1 建模的原理

图1 粒子群算法建模结构图

1.2 问题的提出,目标函数

由图1所示,粒子群算法建模的过程实际上就是函数拟合的过程,这里包括函数的结构和参数。如果我们对被控对象已经有较好的认知,了解其大致的模型,可以先给出其模型的函数结构,再通过粒子群算法辨识出其函数中的参数。假设图1中的输出信号y(t)与输入信号u(t)的关系为:

y(t)=f[u(t)]

(1)

令,t=kTs,(k=1,2,…,Ts)为采样周期,m为采样点数)代入(1)式有

y(kTs)=f[u(kTs)]k=1,2,…,m

(2)

同时假设有:

y(kTs)=fg[u(kTs)]k=1,2,…,m

(3)

如果根据扰动试验得到的m组输入输出数据u(kTs)和y(kTs)同时满足公式(2)和(3),则fg即为所求对象的数学模型。实际上输入输出数据不可能完全满足公式(2)和(3),则可以再假设有:

y(kTs)=fs[u(kTs)]+e(kTs)k=1,2,…,m

(4)

其中,e(KTs)为误差,要想函数fg完全代表函数f,仅需要e(KTs)趋向零。因此可以定义目标函数为:

(5)

1.3 估计模型结构

对于常见的生产过程对象,文献[1][2][3]提出了公式(6)作为通用的模型结构式。

(6)

其中，K为系统增益;τ为纯迟延时间常数;T为系统惯性时间常数;n为惯性部分的阶次;β为微分时间常数;α为常数。

1.4 粒子群算法优化参数

(7)

(8)

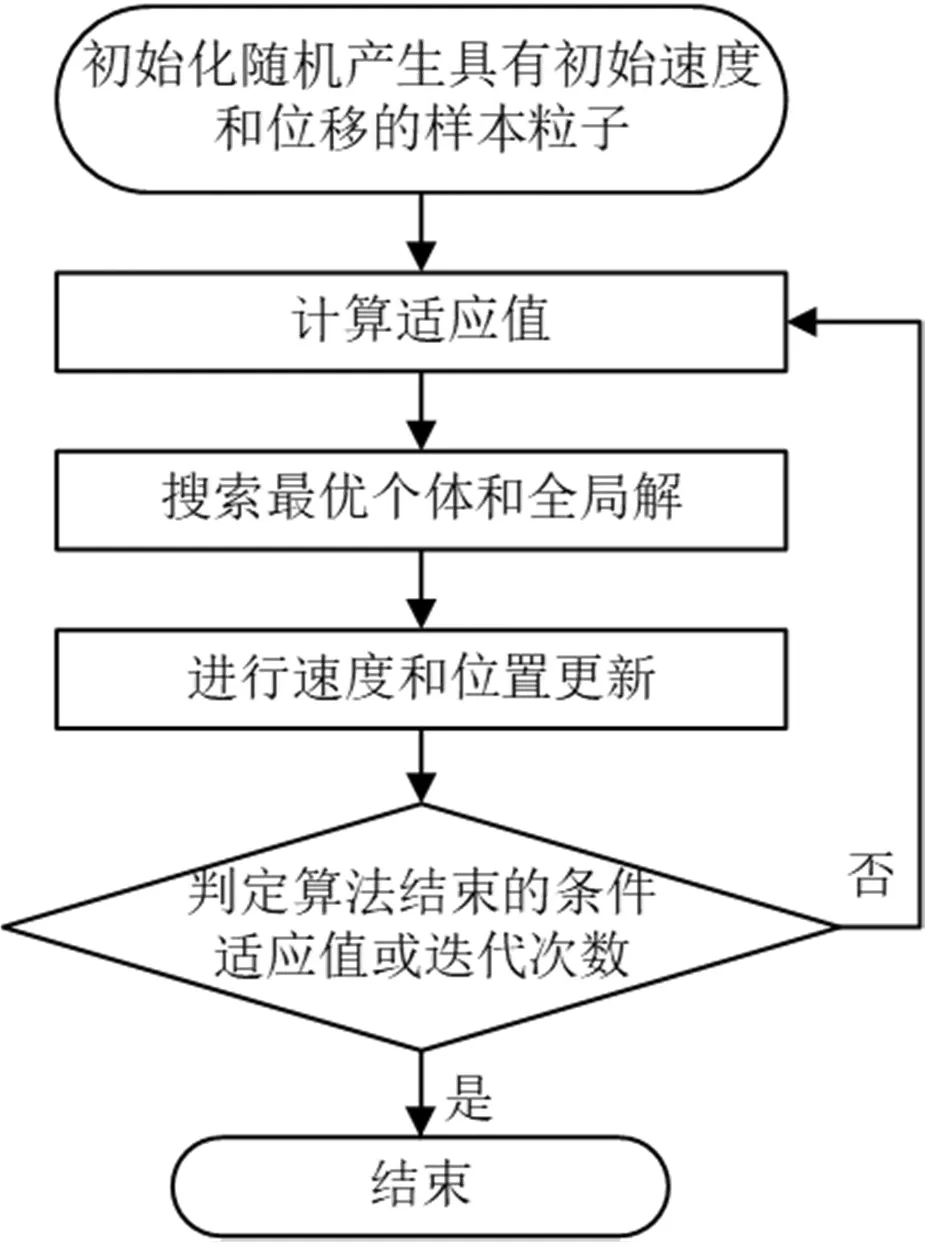
图2 粒子群算法流程图

2 建模实例

现有某多容水箱水位控制对象给水扰动单位阶跃响应实验数据如图3。

2.1 估计模型结构

根据阶跃响应曲线法,从图3水位单位阶跃响应曲线可知,该对象是多容有自平衡对象,估计其模型结构为:

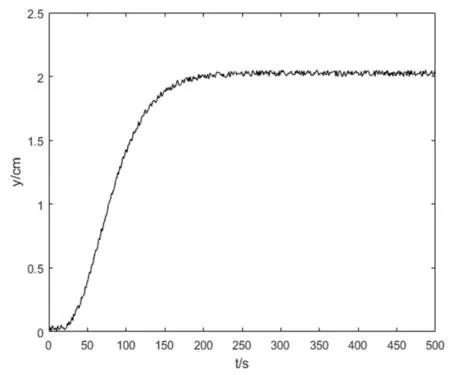
图3 多容水箱水位单位阶跃响应曲线

(9)

2.2 模型参数区间确定

由式(9)可知,该模型参数有4个,分别是K;T;n;τ,下面分别确定各参数的区间范围,由试验建模的阶跃响应曲线切线法画出其切线图如图4所示。

图4 多容水箱水位单位阶跃响应曲线切线图

表1 T、n与τ、Tc的关系

2.3 粒子群算法辨识

应用粒子群算法,设置种群数量为100,空间维数为4,最大迭代次数为200,惯性权重为0.9,自我学习及群体学习因子为0.8,参数的上下限由3.2中参数范围确定,采样时间为1秒,多次运行该程序辨识曲线,如图5所示。返回参数为K=1.9757;T=20.3402;N=4.0111;τ=4.6059;即可认为被控多容水箱数学模型为公式(10)。

图5 辨识曲线

(10)

3 结束语

粒子群算法是一种解决搜索问题的通用方法,通用问题都可以使用。本文将粒子群算法应用在生产过程中的多容水箱模型辨识中,通过输入输出数据,用粒子群算法拟合出系统的传递函数模型。辨识结果表明,粒子群算法能够有效地对生产过程对象进行系统辨识,且具有较高的准确性。