基于增量磁导率的钢轨频变阻抗曲线计算

武伟康，陈剑云，刘思然，傅钦翠

(1.中铁第六勘察设计院集团有限公司 电气化设计院分公司，天津 300250； 2.华东交通大学 省部共建轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013)

钢轨作为牵引供电系统的主要回流导线，其阻抗特性是牵引供电计算和暂态信号分析的重要参数。由于钢轨是铁磁材料，具有非线性的磁滞特性，致使其内阻抗随频率变化更为明显。钢轨内阻抗特性，一般都是基于钢轨基本磁滞曲线的磁导率计算得到。然而，在针对牵引供电系统暂态行波传播特性的研究过程中，暂态行波一般是叠加在大电流基波上的一组高频信号，这些高频暂态信号在钢轨上传播的阻抗特性不同于低频大电流信号。对于低频大电流信号而言，钢轨磁化会不断遍历一个个完整的回形磁滞曲线过程，而对于短暂的高频信号，其变化周期短，幅度相对较小，往往是在基本磁滞曲线的某个点上形成一个小的环形磁化过程曲线，因此，有必要针对高频小信号研究其增量磁导率，并以此为基础，计算出高频小信号的钢轨频变内阻抗特性曲线。

针对一般的牵引供电计算，文献[1-2]对钢轨的内阻抗计算进行了研究，如大电流下钢轨的磁化特性，使用磁导率曲线计算钢轨内阻抗等；并采用有限元方法进行计算，取得了较好的计算结果[3-5]。然而，针对暂态情况下钢轨的内阻抗计算，现有文献资料的研究计算尚不充分。高频暂态信号通常是叠加在稳态大电流基础之上的，即构成了大电流偏置磁场下的小信号增量磁场的情形[6-8]。铁磁材料在暂态信号作用下，会形成局部磁滞回线，且通常定义增量磁导率用来表征铁磁材料的局部磁滞曲线特性[9-11]。此外，有限元方法不仅可以高精度地计算钢轨工字型截面形状，而且可以计算其铁磁特性[12]。多数文献均采用有限元方法[3-5,13-14]计算钢轨的频变阻抗参数。

本文针对目前电气化铁路广泛使用的P60型钢轨展开研究与计算，主要分析研究大电流叠加高频小电流信号作用下钢轨的磁化机理和过程，根据P60钢轨B-H基本磁化曲线，导出钢轨的增量磁导率曲线，并将其添加到Ansys Maxwell计算模型中，计算出暂态情况下P60钢轨宽频率范围(0～10 MHz)的频变阻抗特性曲线。

1 稳态大电流信号下钢轨磁化特性

1.1 钢轨的基本磁化特性

钢轨是典型的铁磁材料，磁导率的非线性变化加剧了电流趋肤效应的程度，使钢轨的内阻抗随电流的变化而更加明显，考虑钢轨的磁化特性是精确计算其内阻抗的前提。在牵引供电计算中，钢轨作为牵引回流的重要导线，可认为钢轨中通以稳态大电流，即处于大电流信号形成的磁场环境中。

在稳态大电流的磁化作用下，其过程具有较强的非线性、时滞性等[9]特点。磁感应强度B(或磁化强度M)对于磁场强度H的关系通常表现为回线的形式，分别被称为磁滞回线和磁滞回线族，如图1所示[15]。

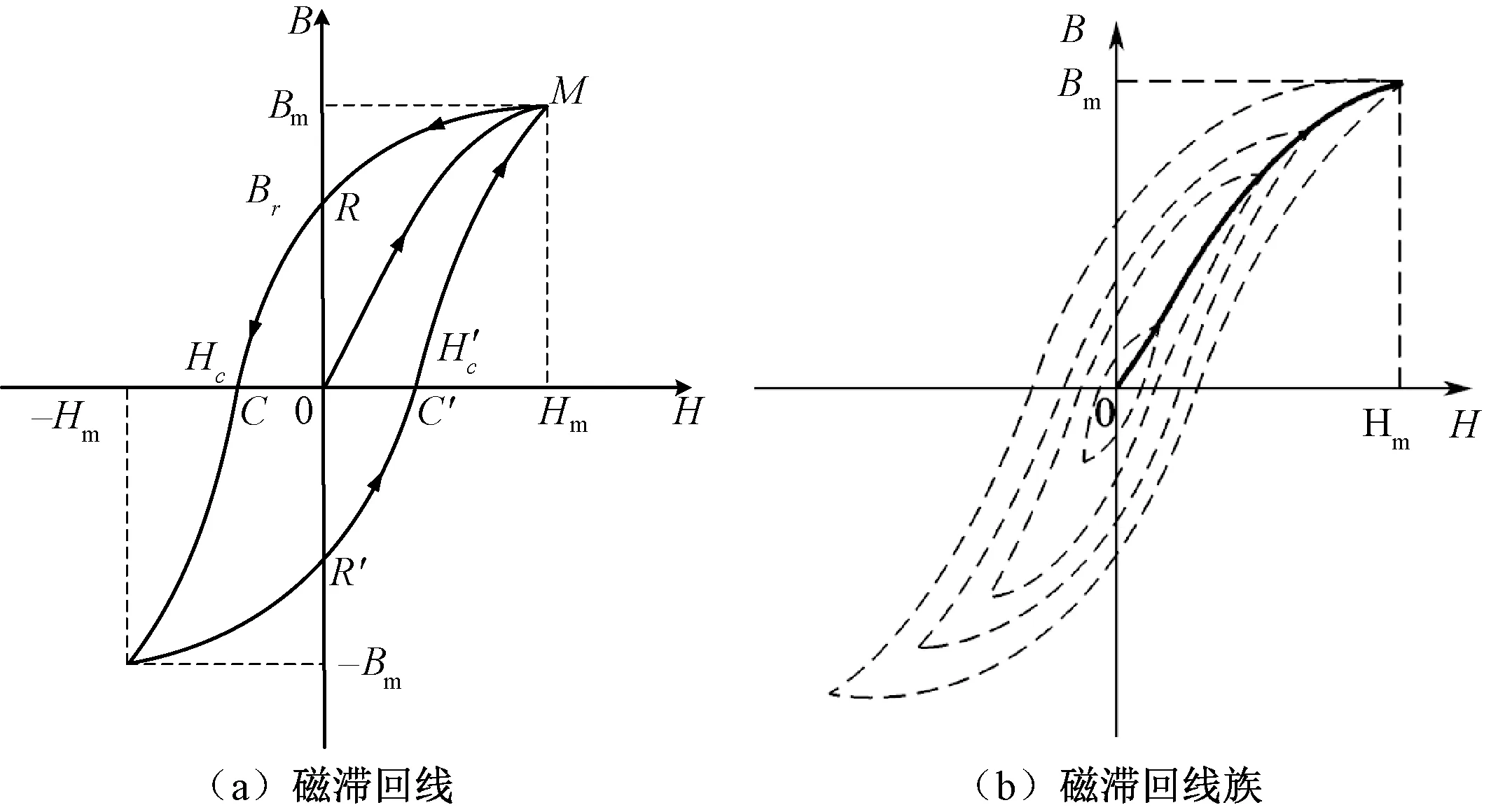
图1 铁磁材料的磁滞回线(族)

磁化曲线是铁磁材料的固有属性，通常由实验方法测定，本文对P60钢轨的铁磁特性进行了检测，获得P60钢轨B-H磁滞回线和基本磁化曲线，如图2所示。P60钢轨其他磁特性参数见表1。

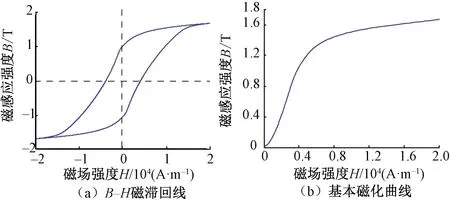
图2 P60钢轨的磁化特性曲线

表1 P60钢轨其他磁特性参数

1.2 钢轨的基本磁导率曲线

磁导率可以定量描述磁性材料的磁化特性，磁场中各物理量之间的关系如下[16]：

对于线性且各向同性材料，通常B、H和M的关系可以表示为

B=μ0(H+M)

( 1 )

若定义材料的磁化率为χm，则有

M=χmH

( 2 )

B=μ0(H+χmH)=μ0μrH

( 3 )

磁导率μ的定义为

μ=μ0μr

( 4 )

为了使用方便，通常使用μr进行计算，即

( 5 )

式中：μ为材料的磁导率；μ0为真空磁导率；μr为相对磁导率。

根据式( 5 )及图2(b)，可以得出P60钢轨的基本磁导率曲线，如图3所示 。值得注意的是，钢轨的磁导率呈非线性变化，计算其内阻抗时不能视其为定值。

图3 P60钢轨基本磁导率曲线

2 暂态小电流信号下钢轨磁化特性

2.1 钢轨的局部磁滞回线

在实际的牵引供电系统中，铁路线路谐波扰动等瞬态情况时常发生，除了稳态大电流的磁场外，还会叠加一些暂态小电流信号，如图4所示。特别是当牵引网发生短路故障时，产生行波等暂态信号，这些信号可能在钢轨的基本磁滞回线内形成局部磁滞回线。

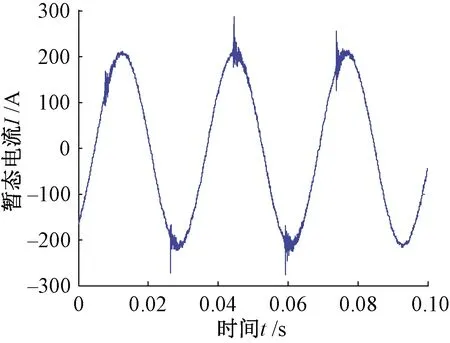
图4 暂态信号扰动下电流波形

如图5(a)所示，假设在回线上的任一点a处，小范围ΔH内往返变化一次或多次，可以生成一条小回线[15](亦称局部回线)。若存在多个不同的偏置磁通密度，则可能会形成多个局部回线，如图5(b)所示。

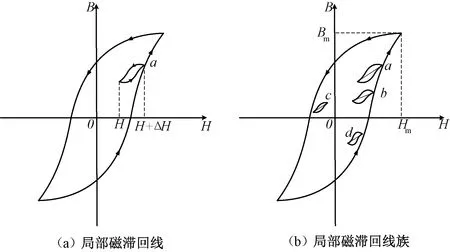
图5 铁磁材料的局部磁滞回线(族)

2.2 钢轨的增量磁导率曲线

如果在一定的偏置磁场强度H下，叠加的小信号磁场的磁化轨迹将以恒定磁场H的工作点为中心形成一小增量环[10]，如图6(a)所示。由于增量环变化周期短，幅值相对较小，可将其近似地做线性处理，取此增量环两顶点间连线的斜率，即为材料的增量磁导率μinc。

( 6 )

式中：ΔB、ΔH分别为磁感应强度和磁场强度幅值的增量。增量磁导率是定义在基本磁化曲线基础上的一种动态磁导率[9]，μinc值也是一条非线性曲线。根据式( 6 )及图2(b)，可以得出P60钢轨增量磁导率曲线，如图6(b)所示。

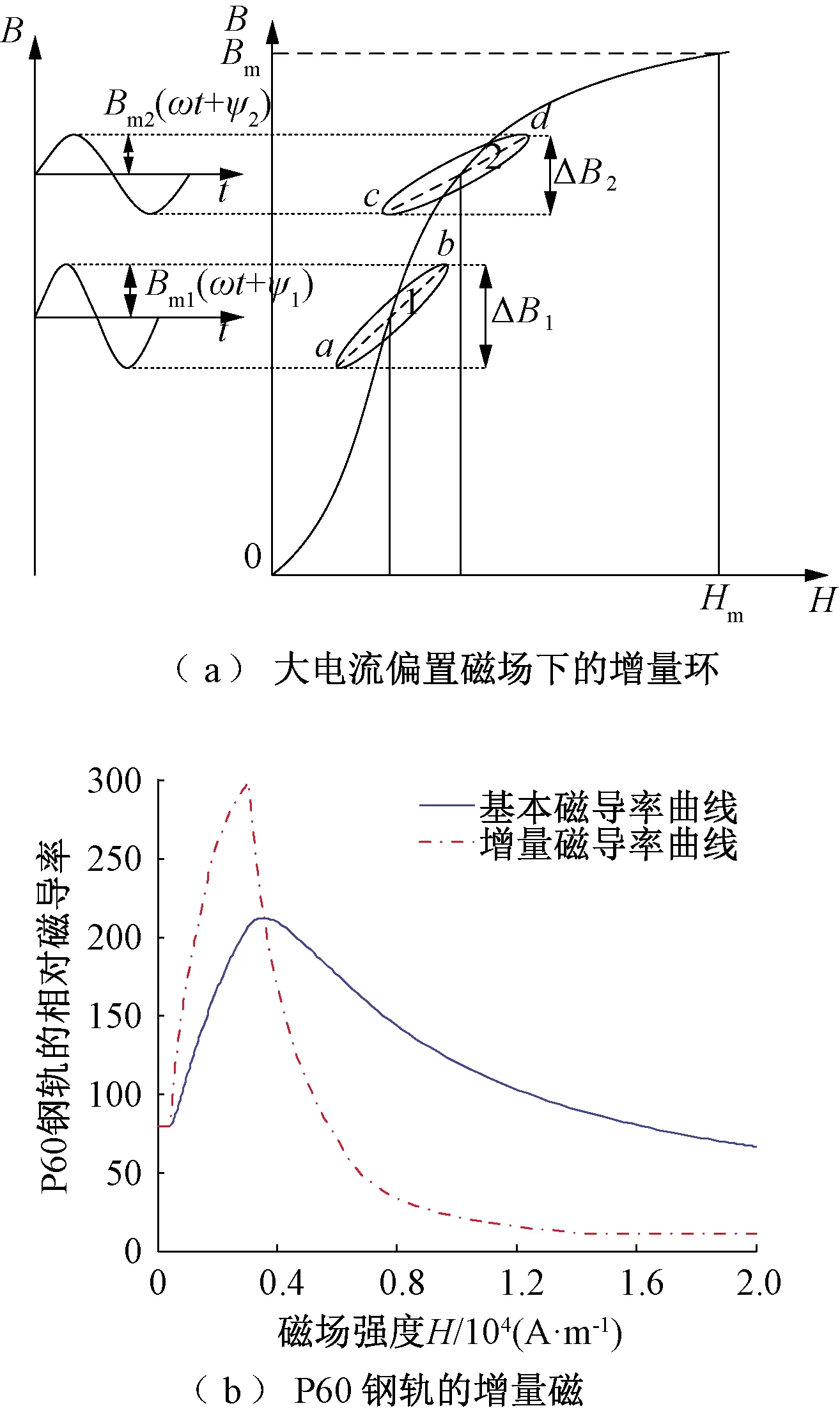
图6 P60钢轨增量磁场下的磁化曲线

3 钢轨内阻抗有限元软件计算

3.1 计算模型边界条件设定

在Ansys Maxwell软件中，导入P60钢轨的Auto CAD图形，建立计算模型，如图7所示。

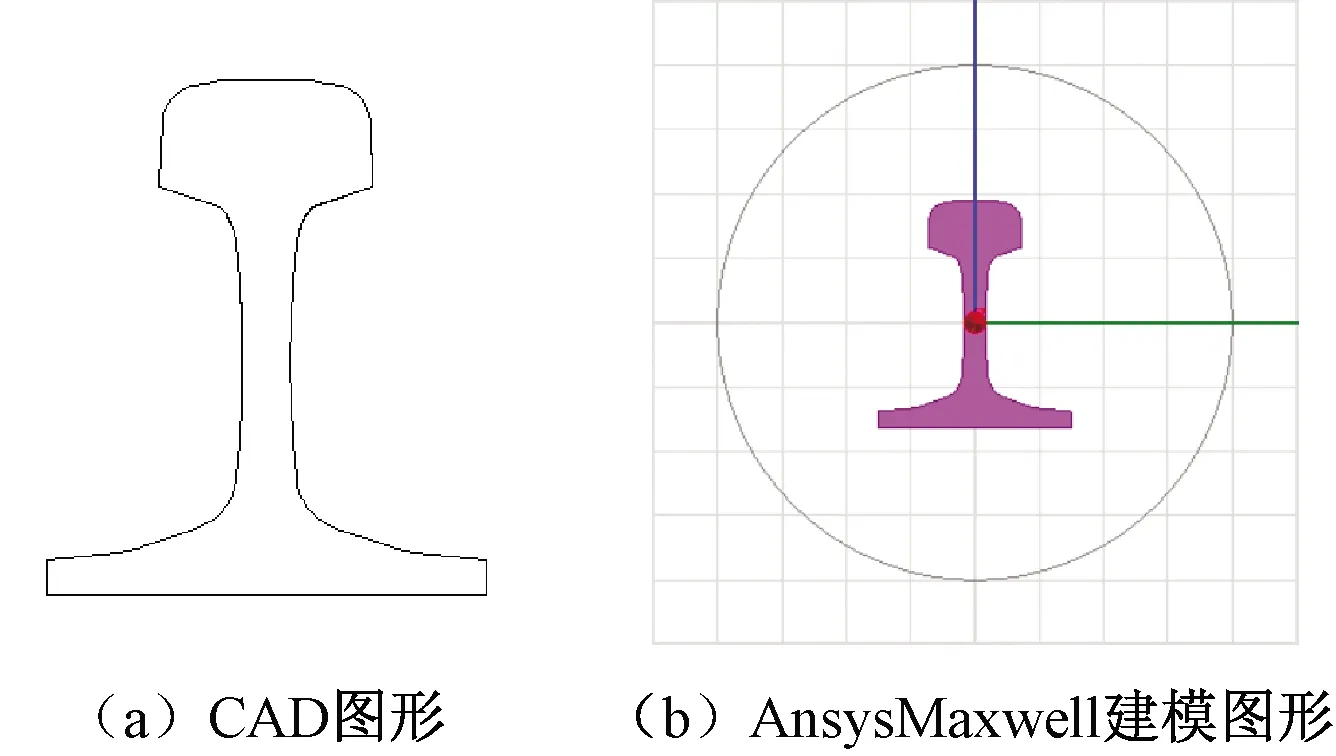
图7 P60钢轨计算模型

设置计算模型参数时，应首先设置场求解器为涡流场，这样可有效添加P60钢轨B-H曲线及其他基本材料属性，见表2。其次，如图7(b)所示，模型中P60钢轨外围设置的圆，外圆半径的大小，只影响模型外电感值，而不影响钢轨的内电感值，仿真计算时也验证了这一点，本文中外圆半径设为R=200 mm。在圆的边界上，设置狄利克雷边界条件；在钢轨上设置电流源激励。在求解过程中，计算钢轨内阻抗的起始频率为0.1 Hz，最高频率为10 MHz，共计127个频率点。

表2 P60钢轨基本材料属性

3.2 P60钢轨计算结果图

计算完成后，可根据需要在计算区域绘制不同类型的场图，P60钢轨的仿真计算结果如图8所示。

如图8(a)所示，对钢轨的网格划分，表层的密集程度大于内部，比较直观地反映出交流电流的集肤效应；图8(b)中钢轨的磁场强度由外向内逐步减弱，中心最弱。图8(c)、图8(d)直观呈现了钢轨内、外部的磁力线分布情况。

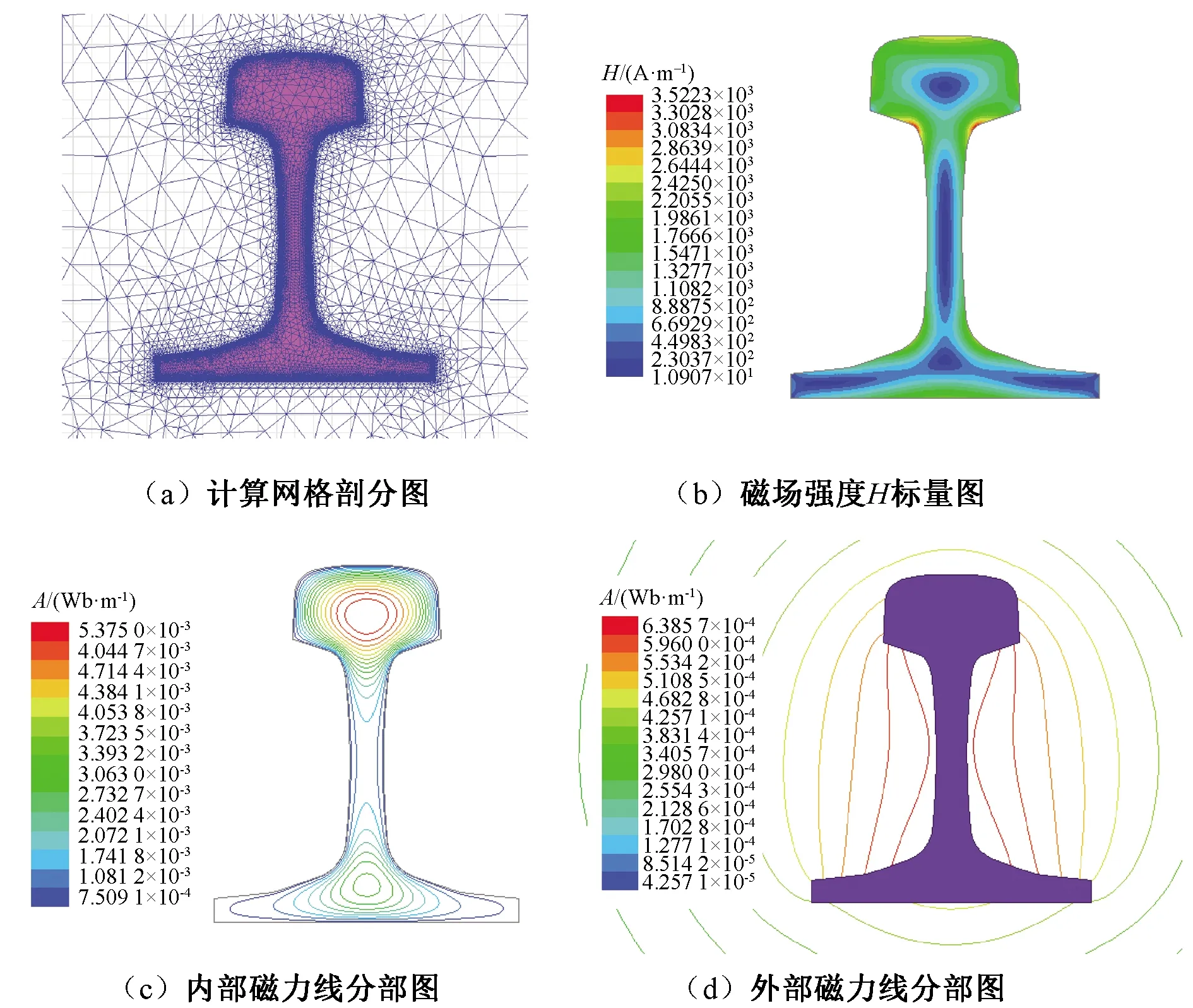
图8 P60钢轨的有限元计算结果

4 钢轨内阻抗频变曲线分析

4.1 直流内阻抗

导体内阻抗包含内电阻和内电感两部分，当电源频率为零时，即为导体的直流内阻抗。可根据式( 7 )、式( 8 )对钢轨直流内阻抗进行计算[17]。

( 7 )

( 8 )

直流电阻Rd与导体的电阻率ρ及横截面面积有关，而直流电感Ld只与导体材料的磁导率有关。由图5(b)可知，P60钢轨的起始相对磁导率μr=79.58，则P60钢轨的直流电阻和直流电感为

2.1467×10-5Ω/m

3.979×10-3H/km

4.2 暂态情况下钢轨的频变阻抗曲线

通过对计算结果进行分析，电流源激励的幅值是影响钢轨内阻抗计算的主要因素，如图9所示。

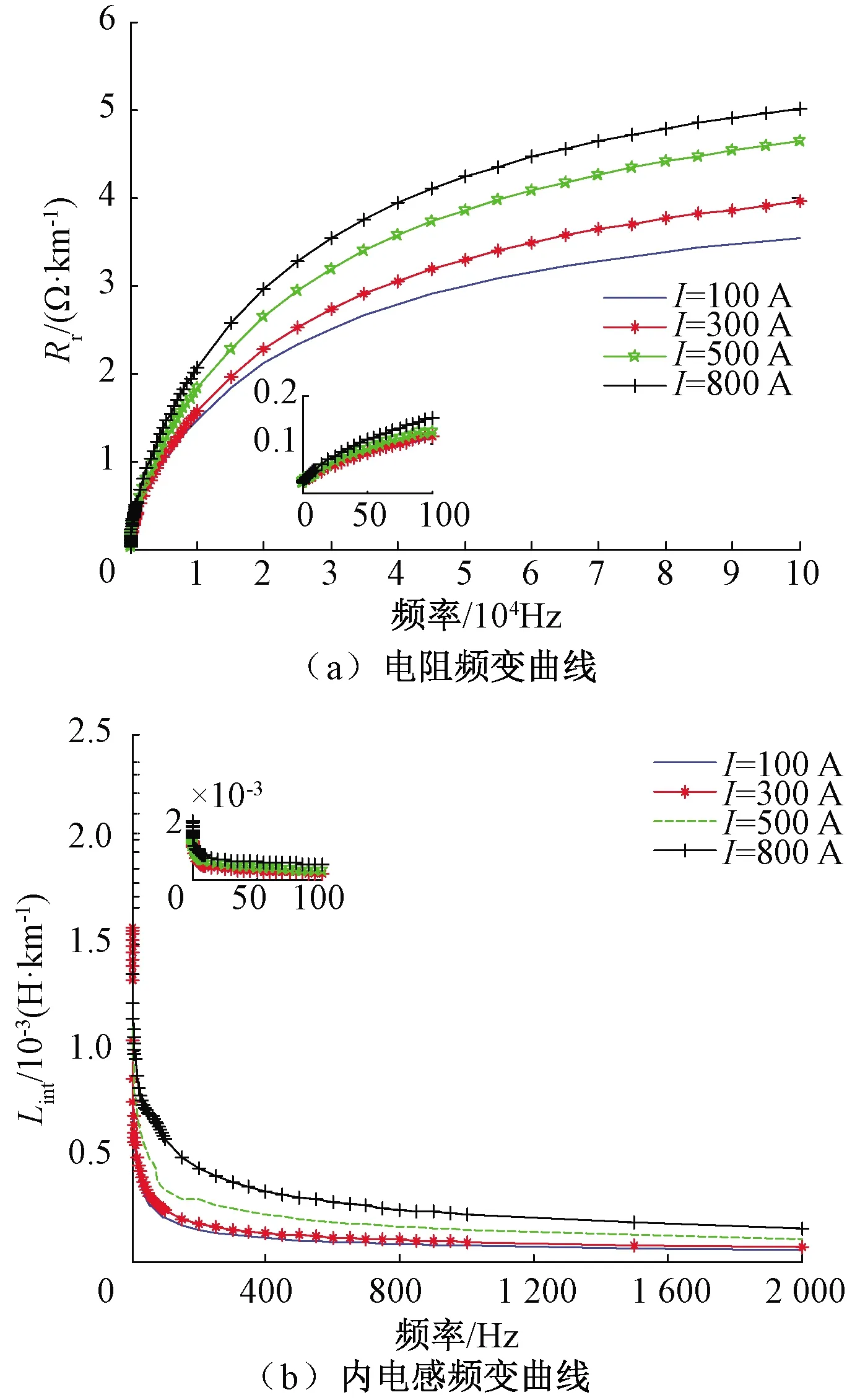
图9 不同幅值电流下P60钢轨阻抗频变曲线

为更清晰地呈现交流电阻Rr和内电感Lint的频变特性，绘图时分别将频率范围设置为0～100 Hz和0～2 000 Hz，以下同理。表3、表4分别给出不同幅值电流源下钢轨的交流内阻及内电感计算结果。

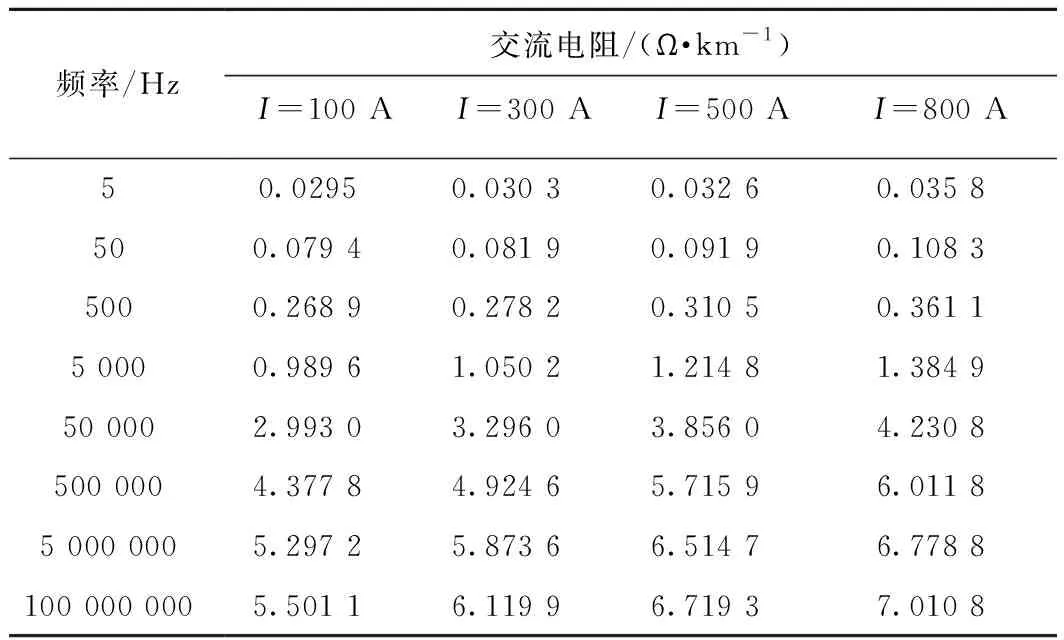
表3 不同幅值电流源下P60钢轨交流电阻值

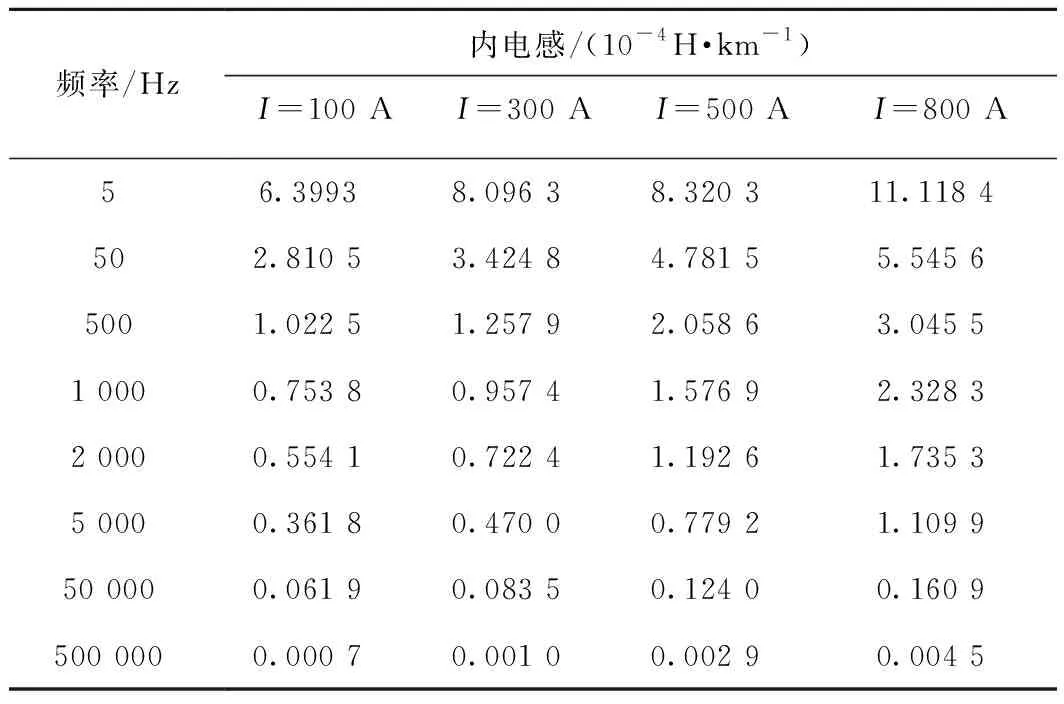
表4 不同幅值电流源下P60钢轨交流内电感的部分结果

4.3 暂态信号扰动与大电流信号频变阻抗曲线对比

通过对比计算高频暂态信号和低频大电流信号下钢轨阻抗频变曲线，可以反应出两者的不同，如图10所示。表5、表6对应图中曲线给出部分计算结果。

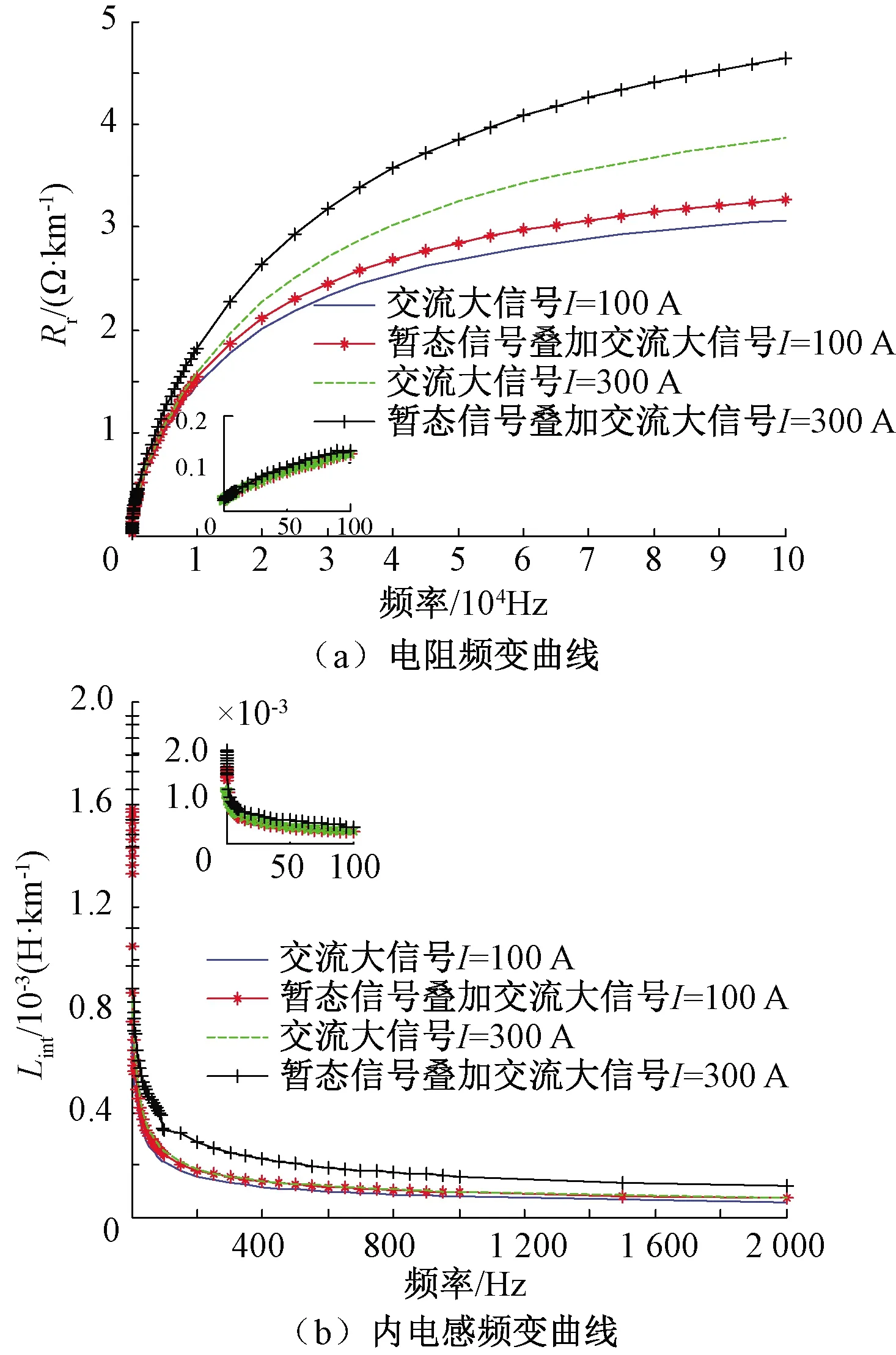
图10 P60钢轨，暂态和稳态下的频变阻抗曲线对比

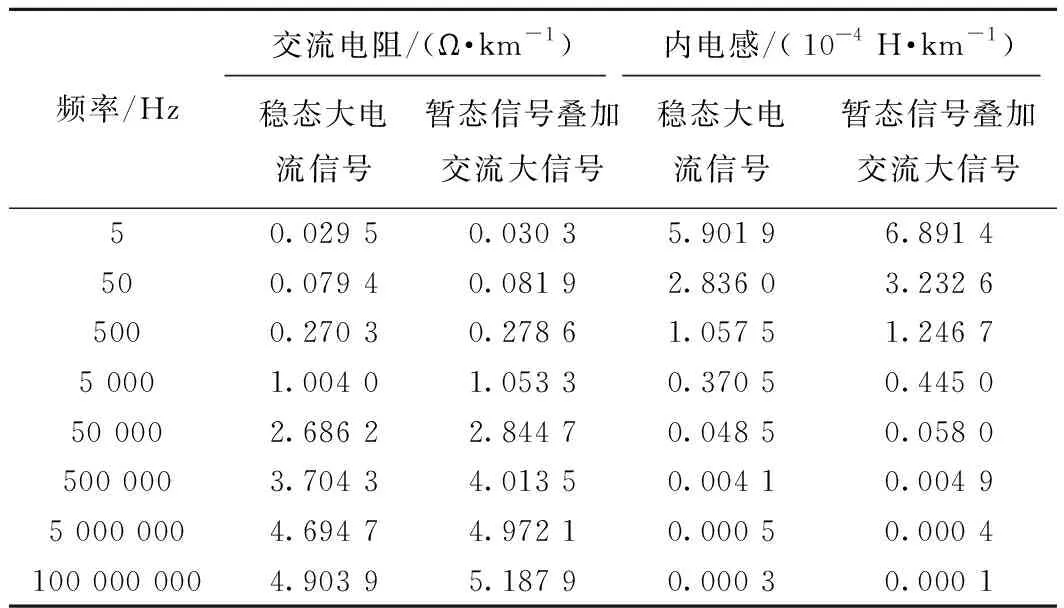
表5 暂态及稳态下P60钢轨交流内阻抗的部分结果(I=100A)

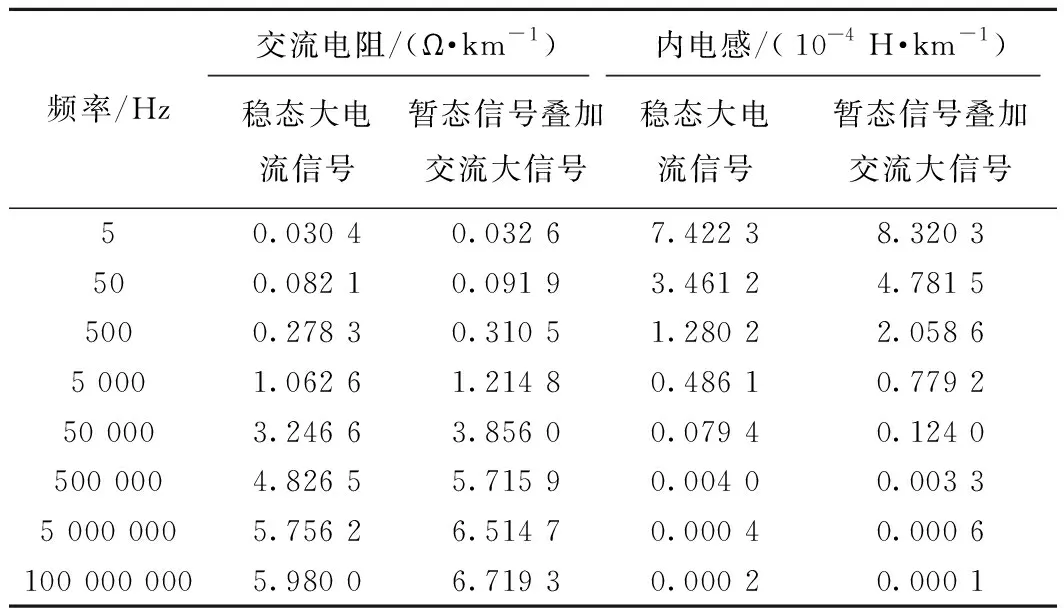
表6 暂态及稳态下P60钢轨交流内阻抗的部分结果(I=300A)

5 结论

通过使用有限元软件Ansys Maxwell，对暂态信号下P60钢轨的磁化机理和特性进行分析计算，并给出0～10 MHz频率范围内钢轨的频变阻抗曲线和具体数值，这些曲线和参数为牵引供电系统进行时频电磁暂态分析提供基本参数。分析计算结果，可以得出以下结论：

(1)钢轨中的电流不断增大时，其交流电阻和内电感值均有所增加；在同一电流下，交流电阻随频率的升高而增大，内电感随频率的升高而减小，且当频率趋于300 kHz时，可近似认内电感减小到零。

(2)高频暂态信号在钢轨上传播的阻抗特性与低频大电流信号不同。高频暂态信号叠加大电流信号形成的增量磁场，使钢轨的交流电阻和内电感值在同一条件下均有所增加，且交流电阻值的差异主要在10 kHz频率以上，内电感值的差异主要在0～5 000 Hz频率段。