移动列车-桥梁系统气动特性风洞试验研究

邹思敏，何旭辉，邹云峰，史 康，欧俊伟

(1.中南大学 土木工程学院，湖南 长沙 410075；2.高速铁路建造技术国家工程实验室，湖南 长沙 410075)

随着国家经济的发展以及基础设施建设的大力推进，截至2020年底，全国铁路运营里程已达14.63万km，其中高速铁路3.8万km。随着列车运行速度和客运量进一步提高，高速列车面临着更为复杂的行车环境，建设与维护的技术难度更大，安全运营过程中将面临更多挑战[1]。

高速铁路车-桥系统是一个庞大又需要多个学科集中交叉支撑的学科体系，而在列车行驶过程中，横风作为无法避免的因素对高速列车的运行安全和舒适性有着重要影响[2]。随着气候与风环境的不断变化及列车运量逐步攀升，因横风所致车辆失稳或倾覆脱轨的事故偶有发生。目前在高速列车气动特性及安全性能的研究中，风洞试验仍是最为行之有效的方法之一。国内外学者对于列车及车-桥系统气动特性研究，大部分采用的是静止节段模型获取列车以及桥梁的气动特性[3]，或通过合成风向角模拟列车运行时与横风的联合作用[4]。这些方法是试验技术不成熟时的近似方法，因此存在以下问题：

(1)列车移动时会改变物体周围的来流风剖面及流场均匀性。

(2)当通过合成风向角进行模拟时，更多是针对列车与来流所形成的风向偏角，而实际上在横风中桥梁或路堤等基础设施则更多是受90°横风的影响。

(3)对车-桥系统而言相对运动产生的气动干扰大，仅仅以静态车-桥组合难以说明问题。

开展桥上移动列车风洞试验的目的旨在更真实有效地模拟列车在实际运动中的运行过程，并探究随着列车移动时，在横风作用下车-桥系统的气动特性及相互作用与影响。

在静态模型车-桥系统试验方法中，作用于行驶车辆上的侧风力通常采用准稳态方法，利用静态模型风洞试验所测得的气动系数进行估算[5]。通常静态风洞实验中的气动特性结果是通过将测量设备安装在基础设施模型上的静态车辆模型来完成。气动特性的测试是通过对车辆和基础设施模型同时进行相同角度的旋转，获得相对于列车所承受的合成风力(这种静态的方式包括二维节段模型试验和通过旋转风向角的方法)。显然，这种模拟方法与实际列车在运行过程中的情况是不同的。在实际列车运行过程中，车辆和基础设施周围流场会因列车的运动发生一系列绕流特性变化，导致横风、车辆及桥梁之间的气动干扰发生了多次变化与转换。因此，这些静态试验并不能很好地反映列车在横风中桥梁上运行时的真实状态。尽管仍有一些研究如运动地板法、边界层吸力法和切向入射法在一定程度上尽力模拟列车运行时的真实场景。然而，正如Cooper[6]所指出的，风切变、湍流的产生及列车与基础设施之间的相对运动只能通过移动的列车模型实验来正确模拟。

移动列车模型试验最早在1981年，使用当时最先进的1∶5比例APT模型在自然风作用下进行，其存在一些不可控制的试验要素[6]。此后在通过风洞试验方法的研究中，文献[7-8] 设计了一个1∶50列车模型，车辆被连接到一个“导轨”上，同时在4个弹性绳的作用下让车辆以5～20 m/s的速度行驶，但此装置需要在风洞地板开槽，导致底部气流对试验结果产生影响。文献[9]开发了一套电机拉动的移动模型并进行了1∶20模型的风洞试验，该设备系统由机械推进和保持车载力的平衡,该设计同时放置了离心鼓风机,提供对侧风来流的模拟。对车-桥系统的绕流特性更为复杂，在风洞试验移动车-桥系统气动特性研究中，文献[10]设计的移动车辆-桥梁模型风洞试验系统，通过伺服马达驱动列车模型在18 m长的导轨上运行。该滑动装置由垂直杆件连接，测力设备安装在杆件上，这个推进系统可以将比例为1∶45的模型车辆以10 m/s的速度进行运行。文献[11] 进行了横风作用下的列车动模型试验，在考虑横风仅对列车气动特性产生影响时，移动试验方法和静态合成风向角法结果之间的差异可能并不十分明显。Premili等[5]通过CFD数值模拟方法的讨论中，指出当存在桥梁等大型基础设施时，列车会与基础设施形成气动干扰，从而对气动特性产生影响。文献[12]也通过风洞试验研究了车-桥系统特性，并认为单独考虑列车或桥梁的气动特性研究会导致车-桥系统的明显误差，车辆与桥梁需当作系统来考虑。

在目前的移动车-桥试验中，常规做法是使用测力天平实现气动力的测量。当测力天平安装在被测车辆模型上时，在每一次移动模型试验中，难以规避在导轨上运动时所引起的车身振动。这些振动将导致机械噪声出现在试验数据的记录过程中，干扰了气动力特性的识别与采集。同时，由于目前这些动模型测试方法在模拟试验时，轮轨接触方式会产生底部气流难以模拟的问题，也存在连接方式所引起的惯性力、摩擦以及连接杆件所引起的气流干扰，从而在测试中难以避免模型振动、扭转和难以测试到局部风压等问题，导致现阶段对于车-桥系统之间的相互气动干扰规律与影响揭示较少。

本文基于中南大学风洞实验室以往的风洞试验研究工作[13]，在移动车-桥风洞试验气动特性测试系统上进行了进一步的优化与升级，并采用高速铁路典型的32 m简支梁桥和CRH2动车组设计了缩尺比为1∶25的车-桥风洞试验模型系统，在风洞中进行横风作用下移动列车在桥上运行时的车-桥系统各自的气动特性测试，该测试方法能够有效方便地对列车与桥梁的表面风压进行采集，从而分析车-桥系统之间静、动态列车在不同风速、不同轨道运行位置的气动特性的相互作用与影响。

1 列车-桥梁风洞试验系统

该试验在中南大学风洞实验室低速试验段内完成，风洞实验室低速段宽12 m 、高3.5 m、长18 m，试验段风速为0～20 m/s。移动车-桥系统为自行研究设计的一套移动车辆模型风洞试验装置U形滑道[13]。该装置除能用于测试车辆停留于桥梁上的静止试验以外，更重要的功能是适用于测试桥上车辆运动时的车辆和桥梁各自独立的气动特性。为尽可能增加试验桥梁长度，该列车-桥梁风洞试验系统横向贯穿整个试验段与来流方向垂直布置，装置基于势能转换为动能的原理，可将模型列车牵引至预定高度进行释放，列车通过自身重力加速向下滑行，以达到一定的初速度进入试验段。试验装置总长度为14.5 m，两侧加速滑道顶端距离桥面高度为4.5 m，其中试验列车模型在桥上运行距离为6.4 m，为满足风洞阻塞比的要求，车-桥系统模型缩尺比为1∶25，将阻塞率控制在3.4%，试验总体布置如图1所示。

图1 车-桥风洞试验系统总体布置

由图1可知，两侧滑道采用钢结构支架进行支撑，而在桥梁部分为更好模拟实际桥梁的气动外形，采用相似气动外形的钢制桥墩进行支撑布置。两端滑轨的外侧分别安装对模型进行牵引拉力的卷扬机，同时为了方便试验可多次重复操作，避免因人为操作所引起的风洞使用问题，在提升卷扬机钢丝缆绳的前段连接一辆牵引运动小车，该小车可沿轨道方向运动，且可通过在风洞外远程操控进入风洞试验段内，通过控制小车和提升卷扬机将高速列车模型提升至预定高度完成试验。该加速方式可通过调整模型的高度提供实现高速列车模型瞬时加速的动力以及所设定的预定速度，而两端滑道的对称布置则为了方便运动的列车在短时间内通过动能转化为势能，从而将能量进行耗散，达到减速直至自然停止。模型最大速度可达12 m/s，该装置操作方便快捷，可重复性强，有效缩短了测试时间，提高了试验效率，且可使列车在桥梁轨道上实现双向对开。

车-桥模型与实际高速列车和桥梁结构几何外形相似，列车模型如图2(a)所示。考虑模型在桥上匀速运行的有效试验时间、距离和稳定性等，试验模型采用“头车+中车”的两节编组，头车模型长度1 028 mm，中车模型长度980 mm。列车和主梁模型采用优质木材制作，保证模型具有足够的刚度，试验中模型不发生变形且不出现明显的振动现象，以保证压力测量的精度。车厢之间相互独立，通过连接装置保持车厢之间的间隔。试验以中车为测试对象，头车作为气动过渡段，以保证中车运行过程中的气动稳定性。同时，为更好地保持气动外形高度的相似性，试验桥梁按照原型桥布局设计，在桥梁上采用“双轨制”。轨道高度、轨距、轨道中心间距严格按照1∶25比例制作和安装。为了保证列车运行的稳定性和提高测量精度，选用金属扣件将轨道每10 cm固定一次(与实际轨道铺设固定方式类似)。此外，试验中还采用了钢轨夹轨轮，保证列车模型的安全稳定，风洞试验模型如图2所示。

图2 风洞试验模型(单位：mm)

2 测试系统

列车表面风压数据采集系统采用自主研制的无线测压系统。系统位于中车车身内部通过测压管与列车表面测压孔相接，因此可直接获取中车的表面风压，并实时将采集到的风压数据通过无线的方式传输到远程计算机上，有效避免了传统压力扫描阀等带来的拖线问题以及测力天平抖动导致的惯性力问题，使该测试系统可承载且适用于此种类似移动物体气动特性的测试，试验中采样频率为1 kHz，压力测试精度为0.1 Pa。在试验中，静止/运动列车在横风作用下的表面风压数据可通过该采集系统获取，并可将数据实时发送至远端的上位机上。列车测试结果仅考虑列车在桥梁上的气动特性，桥梁气动特性由DSM3400压力扫描阀测得，采样频率为625 Hz。

车辆速度测量采用两个光电开关和两个激光位移计进行。传感器利用激光工作，可感知探头与物体距离的范围为30 cm。为获取列车速度，将传感器进行一定间隔距离布置，测量探头间隔为66.5 cm。由于速度是两个传感器之间的距离与时间的比值，通过本方法的设置获得试验中模型列车的速度。探测的持续时间是将车头运行至车尾，并且可通过不同高度释放列车获得不同的列车变化车速。速度测试设置在试验桥梁前与滑道的相接处，因此可得到列车在桥上运行时的速度，由于运行距离较短，且在桥梁段前后两侧探测速度损失较小，因此可认为该试验在列车进行平缓桥梁试验段时为匀速运动。

3 试验工况

为更好得到列车气动力特性，试验针对中车模型进行了风压测试，同时为探究列车对桥梁气动特性的影响，试验中，在桥梁跨中位置，沿桥梁截面布置了29个测点，车辆以及桥梁风压测点位置如图3所示。为分析动、静模型在横风作用下车-桥系统气动特性的差异，试验分别针对不同风速、车速以及车辆位置对车-桥系统进行气动特性测试，分析各因素对车-桥系统气动特性的影响。试验在低速试验段进行，每种工况分别设置3个试验风速(8、 9、10 m/s)，列车速度分别为0、4、6 m/s 3种车速，以及不同的轨道位置(先受到横风影响的一侧为上游轨道)，如图4所示。为减小动态试验数据的误差并兼顾试验效率，保证试验结果的精度以及准确度，对移动列车每一个工况重复进行10次试验。

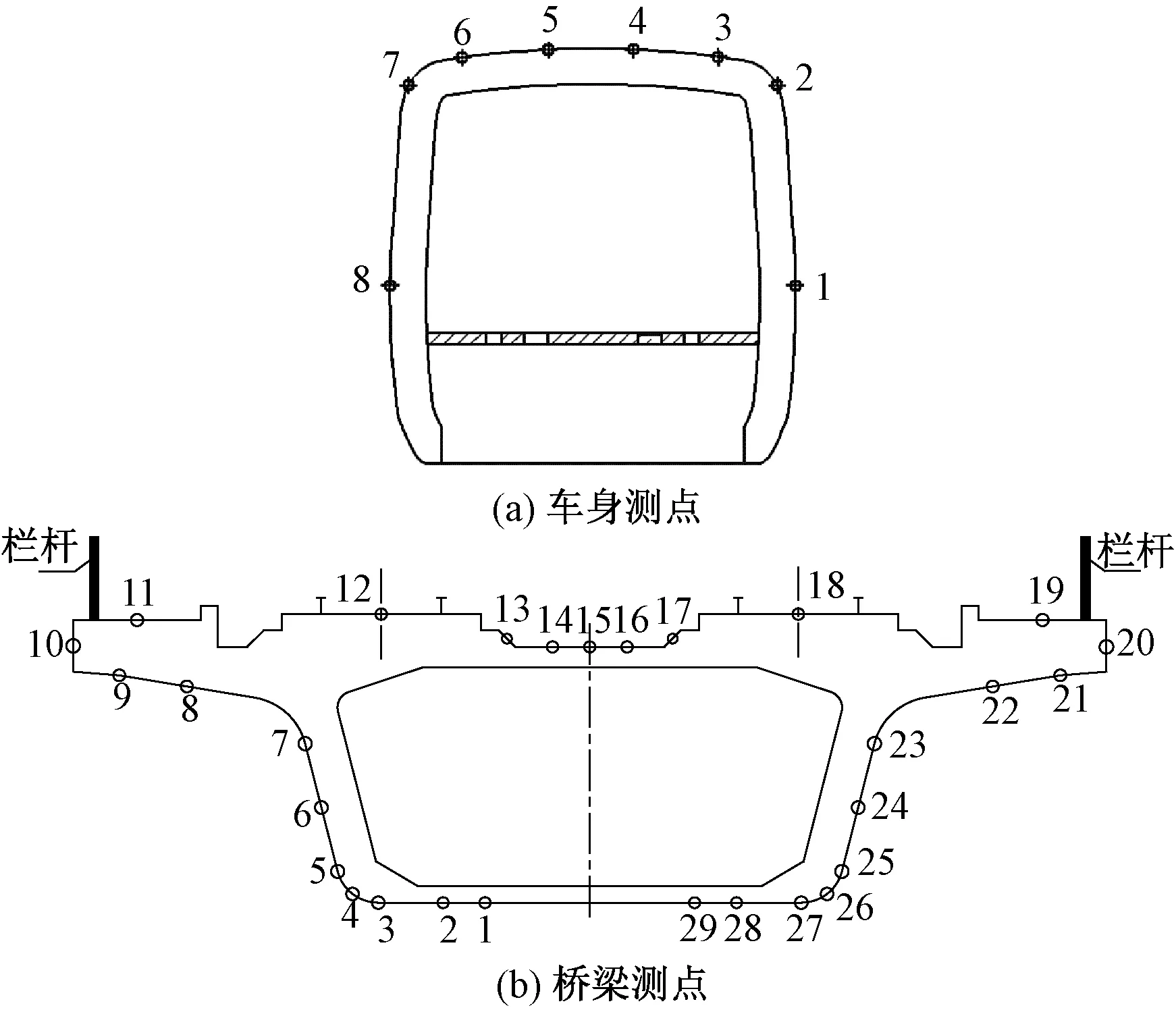
图3 车、桥断面测点位置及编号

图4 列车运行于不同轨道位置

4 数据处理方法

利用测压技术对桥梁和列车进行测压，可以得到桥梁和列车表面的压力分布，每一点的风压可以用压力系数Cpi进行描述。

( 1 )

式中：Pi为试验测点处测得的风压，以指向试验模型表面的压力为正；P∞为风洞内试验参考高度处的静压；U∞为参考高度处风洞来流风速，即取风洞试验风速；ρ为空气密度，通常取1.225。

5 试验结果分析

5.1 列车表面风压5.1.1 静动态差异

图5和图6通过移动和静态试验比较了随着风速变化沿列车截面的压力分布。从各监测点数据来看，移动列车风压系数的分布明显与静态列车不同，这是由于列车运动时产生的强烈三维效应和侧风的偏航角造成的。

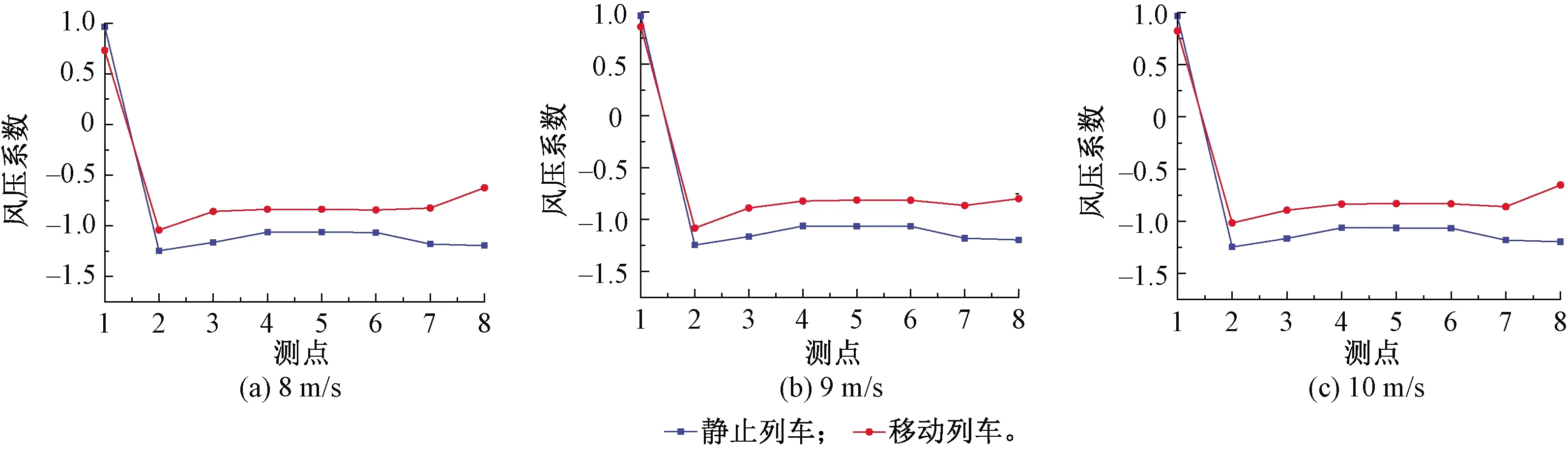
图5 不同试验风速列车表面平均风压系数的比较 (上游)

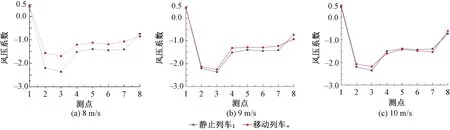
图6 不同试验风速列车表面平均风压系数的比较 (下游)

图5为静止列车和移动列车在上游轨道时的压力分布。在列车处于静止情况下，除迎风面外，所有试验的风压系数Cp均为负。静态情况下的Cp值远大于移动情况下的Cp值。这是因为列车的绕流特性在静态和动态之间是从90°钝体绕流状态过渡到小偏航角的细长体绕流状态[14]。对于下游轨道列车，风速为8、9、10 m/s时，迎风面压力为正，其余为负，如图6所示。在所有试验中，位于列车车肩附近的点3的压力负值最大，也表明了气流在点3附近产生了强烈的分离。此外，移动列车的Cp分布随风速而变化，主要在列车顶部和尾部之间。首先，两种试验方式所获得的列车表面压力有接近的趋势，表明在下游区域时列车会进入下游桥梁提供的低压区，并受到由桥面前缘引起屏蔽效应。然而处于上游运行的列车更容易受到侧风的影响，也因为车辆在此位置时受到侧风的直接影响更大。相对于上游，当列车在下游时迎风面和背风面的压力差异变得较小。此外，通过对比图5和图6的结果可以发现，在相同风速和列车速度的不同轨道上，分别使用静止和移动模型时，Cp分布有较大的不同。这一观察结果表明，使用风速和列车速度矢量的合成并不能完全揭示列车在桥上运行时的空气动力特性。在这种情况下，火车与桥梁之间的相对运动可能起着不可忽视的重要作用。

5.1.2 风偏角的影响

列车的运行速度与来流风速形成一定的风向角，如图7所示。其中，U为侧风速，V为列车速度，W为列车合成速度，α为列车速度与相对速度之间的风向偏角。合成风向角工况见表1，其中合成风向角为侧风风向与列车前行方向的夹角。

图7 合成风向示意

表1 风速与车速工况合成风向角

图8为0、4、6 m/s 3种列车速度，风速为8、9、10 m/s情况下Cp的比较。图8中每个子图对应的是3种不同列车车速下不同的恒定侧风风速。

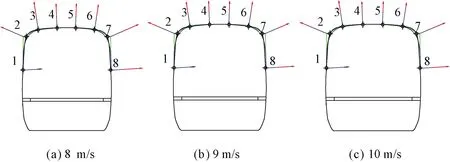
图8 不同风向角下的列车表面风压

由图8可知，风压系数与偏航角之间存在着紧密联系。通过3种不同颜色的箭头长度表示不同偏航角下的风压系数差异。图8中，相对较长的红色箭头表示偏航角为90°时静态情况下的Cp值，根据图8所示，此时风压系数在所有情况下均呈现出相对较大的数值结果。而且，在不同风速条件下，偏航角为90° 静态工况的风压系数均呈现类似相同的趋势。此外，通过对比发现，在移动和静止模型试验中风压系数的变化出现一些明显差异，因偏航角的转变而不同，特别是当偏航角小于60°时。由于偏航角的变化由车速和风速变化组成，在这些偏航角中，56.31°和90°偏航角下，列车的表面风压系数相对于其他工况更为接近。当偏航角小于60°时，可以发现每个风压测点的一些其他变化，特别是在靠近列车顶部和前缘车肩的位置。这些风压系数随列车车速和风速变化而变化的规律，说明了列车在桥上运行时余弦定律不再适用。这些静动态列车之间的差异是由于列车与桥梁之间的相对运动造成了周围一系列绕流特性发生变化，当列车运行时，列车周围的绕流效应将产生更多瞬态和不规则的涡旋流动，造成瞬态速度波动和额外的附着湍流[14-15]。

此外，侧风对桥梁产生的湍流通常与流动的分离和再附有关，而湍流的影响将直接影响列车的气动特性。但是，这里需要指出的是由移动列车在桥上运行时引起的非定常效应，在文献[16-17]中也发现了相似的规律，当列车在箱梁和桁架桥梁上运行时，气动力系数因偏航角引起的变化规律导致余弦准则不再成立。在一定偏航角下，气动力系数随偏航角的变化而变化。在这种情况下，侧风作用下行驶的列车被一个复杂流场所包围，桥的存在会进一步加剧这种绕流特性的复杂程度。

5.2 静、动态列车对桥梁表面风压的影响

图9为不同列车运动状态下，不同风速和轨道位置对桥梁的影响。图9(a) 为单独桥梁未有车辆对桥梁进行干扰时所获得的典型简支箱梁桥截面的平均压力分布。桥梁迎风面为正压，其余3个面即顶面、背风面和底面所受风压为负。在靠近迎风面的底部角落出现较高的负压值，可能是由于从这些拐角处涡流分离的剪切层中流动分离所引起的强夹带和吸力。与迎风面的压力值相比，下游面的压力值较为平稳且接近。

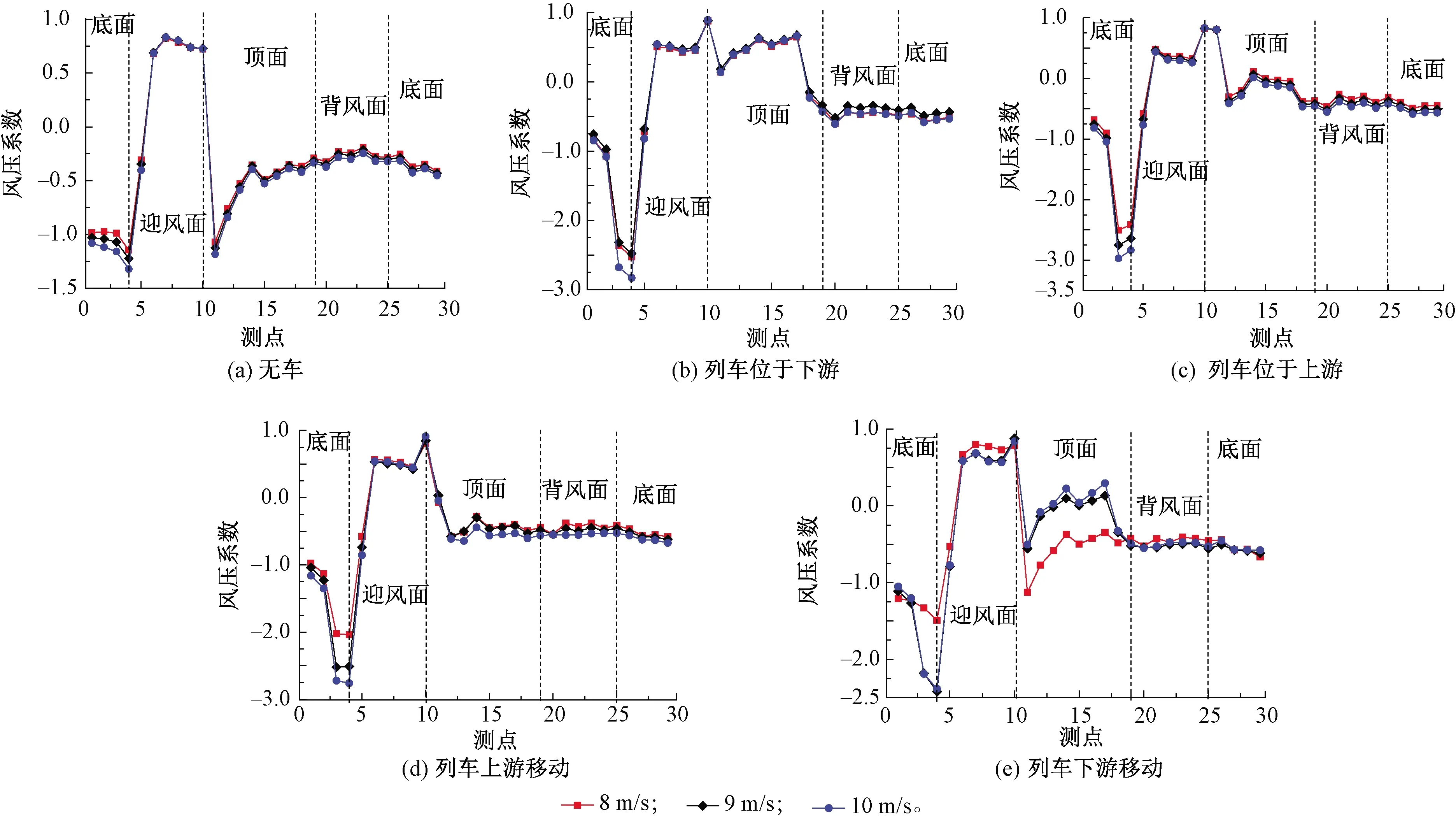
图9 桥梁表面平均风压系数

为进一步比较列车导致的桥梁气动特性变化，图9(b)、图9(c)为静态列车在桥梁上游和下游轨道时，平均风压沿桥面轴线的分布。桥梁的平均风压系数由于列车的存在而发生改变。这源于列车固有的三维结构特性改变了桥梁前缘的流场。桥面前缘底部平均风压呈现出极大的负值，在不同风速影响下出现较大的差异，且随着风速的增加风压系数也增大，而其他区域风压分布在不同位置上的变化趋势是相似的。在桥梁前缘底部出现这种不一致极大可能是随着风速的增加，流动分离位置和边界层过渡而导致的结果。由于列车直接位于桥梁上方，因此桥梁顶面的压力分布是与列车位置直接相关的，而且不同的位置对分布影响较大。相比之下，桥梁顶面未出现明显负压，这是因为通过车与桥之间的间隙流动被限制在很小的区域内，因此没有强烈的流动分离。此外，背风侧和下游底部的压力差异相对于迎风区和顶部的差异较小。

图9(d)、图9(e) 所示为移动列车工况下桥梁的压力分布。如图9(d)所示，桥上的平均风压分布受上游车辆运动的影响。在桥梁迎风部分，风压分布和前述工况的分布有较大的不同。除前缘底部呈现出强烈的负压外，迎风面的正压减弱。对于车辆位于下游情况(图9(e))，列车在移动的情况下，前缘底部和顶面的风压变得容易受到列车移动的影响。这是因为列车的运动对周围的流场影响导致桥面的压力发生变化。从图9(d)、图9(e)还发现，当列车在下游轨道运动时，风速的变化对桥梁气动特性的影响较前三工况更大。此外，通过对比图9各工况可以发现，列车不同状态下导致的风压系数分布与其他情况有较大的不同。这一结果进一步表明当桥梁和车辆同时使用静止试验遭受风偏角为90°的影响时，并不能完全揭示列车运行时桥梁的气动特性。

6 结论

车-桥系统的气动特性风洞试验测试常采用静止节段模型获得，但车-桥系统移动列车风洞试验在系统的气动特性研究上正愈发展现出其优势。本文采用中南大学风洞实验室自主研发的车-桥气动特性风洞试验系统对列车表面风压以及桥梁气动特性进行风洞试验研究，该系统可方便改变来流风速、车辆运行速度以及相对位置等，通过对车辆表面风压以及桥梁气动特性的分析，得到以下结论：

(1)在横风作用下，列车表面风压受到列车在桥上行车位置的影响，列车在下游运行时，列车表面风压受列车静、动状态的影响较小。

(2)当列车在桥上运行时，在车-桥系统气动特性研究中，由于受到桥梁的气动干扰，合成风向角法变得难以成立。

(3)与静态试验不同，在横风作用下车辆在桥梁上运行时，风速对桥面气动特性影响十分敏感，特别是在下游轨道区域。

(4)列车在桥上运行时，会对桥梁的气动特性产生更明显的干扰，会因此引起风-车-桥系统气动耦合效应，引起结构振动，对行车安全与舒适性产生影响。