高速列车受电弓气动噪声分析与弓头降噪研究
袁贤浦,苗晓丹,袁天辰,杨 俭
(1.上海工程技术大学 城市轨道交通学院, 上海 201620;2.上海工程技术大学 机械与汽车工程学院, 上海 201620)
随着我国高速列车的快速发展,各城市之间的互联互通效应越来越强,然而随着列车速度的不断提高,噪声问题也愈发突出。高速列车噪声包括轮轨噪声、牵引噪声、气动噪声等,当速度达到或超过250 km/h时,气动噪声的影响逐渐显现[1]。高速列车气动噪声指的是列车在高速运行时车体壁面与空气相互碰撞,车身表面脉动压力产生的噪声以及尾涡脱落产生的涡激噪声[2]。研究表明,车头、转向架、空调导流罩特别是受电弓等车体的突出部位气动噪声尤为突出[3]。高速列车运行时为偶极子声源,声压级与运行速度的六次方成正比[4-5]。复兴号最高设计速度为400 km/h,气动噪声尤其明显。因此本文对复兴号高速列车的受电弓气动噪声展开深入研究。
目前研究高速列车受电弓气动噪声的主要方法有试验研究以及数值模拟研究。
试验研究主要包括线路实车测试和风洞试验两种方法。线路实车测试侧重于获得列车运行时的所有真实噪声数据,很难将气动噪声单独分离出来[6]。风洞试验可以准确地控制试验条件,精确性较高,可有效对气动噪声进行分离,但是其试验数据会受到列车缩比模型尺寸、地面效应、风洞尺寸大小等影响[7],且风洞试验成本昂贵,在成本有限的情况下无法多次试验。
利用数值模拟求解气动噪声分为两类:计算气动声学方法(CAA)、Lighthill声类比方法[8]。虽然理论上计算气动声学方法(CAA)是最精确的方法,但是由于其直接求解流场和声场需要极大的计算量,求解时非常耗时,因此并不适用。最常用的方法是Lighthill声类比方法[9]。文献[10]根据涡声理论通过数值模拟计算了高速列车受电弓的气动噪声,并分别对低频和高频噪声产生机理进行分析。文献[11]通过对高速列车外部非稳态不可压缩流场进行分析,应用声类比理论计算分析列车表面气动噪声产生机理。近年来国内学者也广泛利用CFD技术和计算声学方法对高速列车气动噪声问题展开了分析。文献[12-13]基于Lighthill声类比理论,对DSA380双碳滑板受电弓气动噪声进行数值模拟,对受电弓开、闭口两种运行方式的气动噪声进行对比分析,并提出对应的降噪改进意见。文献[14]采用Lighthill声类比理方法,对CRH380A型高速列车整车模型进行数值模拟,对高速列车气动噪声在声屏障作用下的传播规律等进行了研究。文献[15]采用Lighthill声类比方法计算高速列车表面噪声源,并对车内气动噪声进行降噪方法的研究。文献[16]基于Lighthill声类比理论计算了高速列车受电弓噪声源特性,提出一种主动射流降噪方法,对受电弓底部空腔进行了降噪研究。文献[17]以FW-H声类比法为基础,完成了速度500 km/h高速列车车头外形的综合评估和优化设计。现有研究只有对受电弓开闭口方式、受电弓底部空腔、声屏障、车内及车头部位进行过气动降噪分析,而对受电弓弓头的降噪研究还处于初级阶段,因此本文提出一种弓头仿生结构优化降噪方法,对单碳滑板受电弓进行噪声分析和降噪研究。
通过建立复兴号高速列车整车气动噪声分析模型,对其单碳滑板受电弓各部位的气动噪声贡献量、远场传播规律和频域分布规律展开研究。分析受电弓主要噪声源弓头的气动噪声形成原因,对受电弓弓头进行了仿生降噪设计并探究降噪效果。
1 气动噪声分析模型建立
1.1 三维几何模型
以复兴号高速列车为参考模型,研究对象为车顶受电弓。为了更好地模拟受电弓前端来流状态,建立三节编组(车头、带受电弓车厢、车尾)的列车简化模型。为减少网格数量,缩短计算时间,不考虑转向架、车门、车窗等部件,对车顶受电弓进行适当简化,忽略对气动噪声影响不大的细小零部件;保留受电弓底部空腔、车厢连接处等对受电弓尾部湍流产生较大影响的部位。
复兴号八节编组,整车有开口和闭口两个受电弓,受电弓由弓头、上臂杆、下臂杆、平衡杆、底架、绝缘子等结构组成。本文对噪声较大的闭口受电弓[18]进行研究。在不影响受电弓前端来流状态的前提下将列车简化为三节编组,模型总长为79.50 m。列车简化模型以及受电弓简化模型如图1、图2所示。
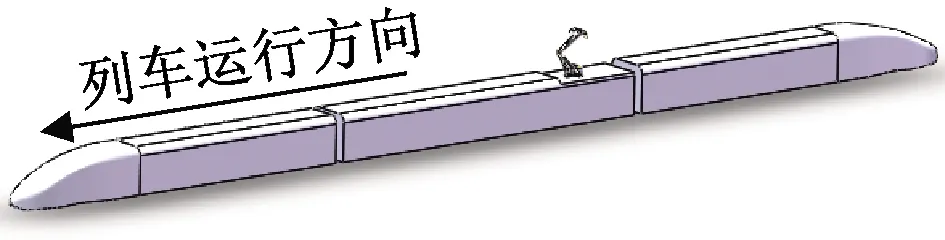
图1 三节编组列车简化模型
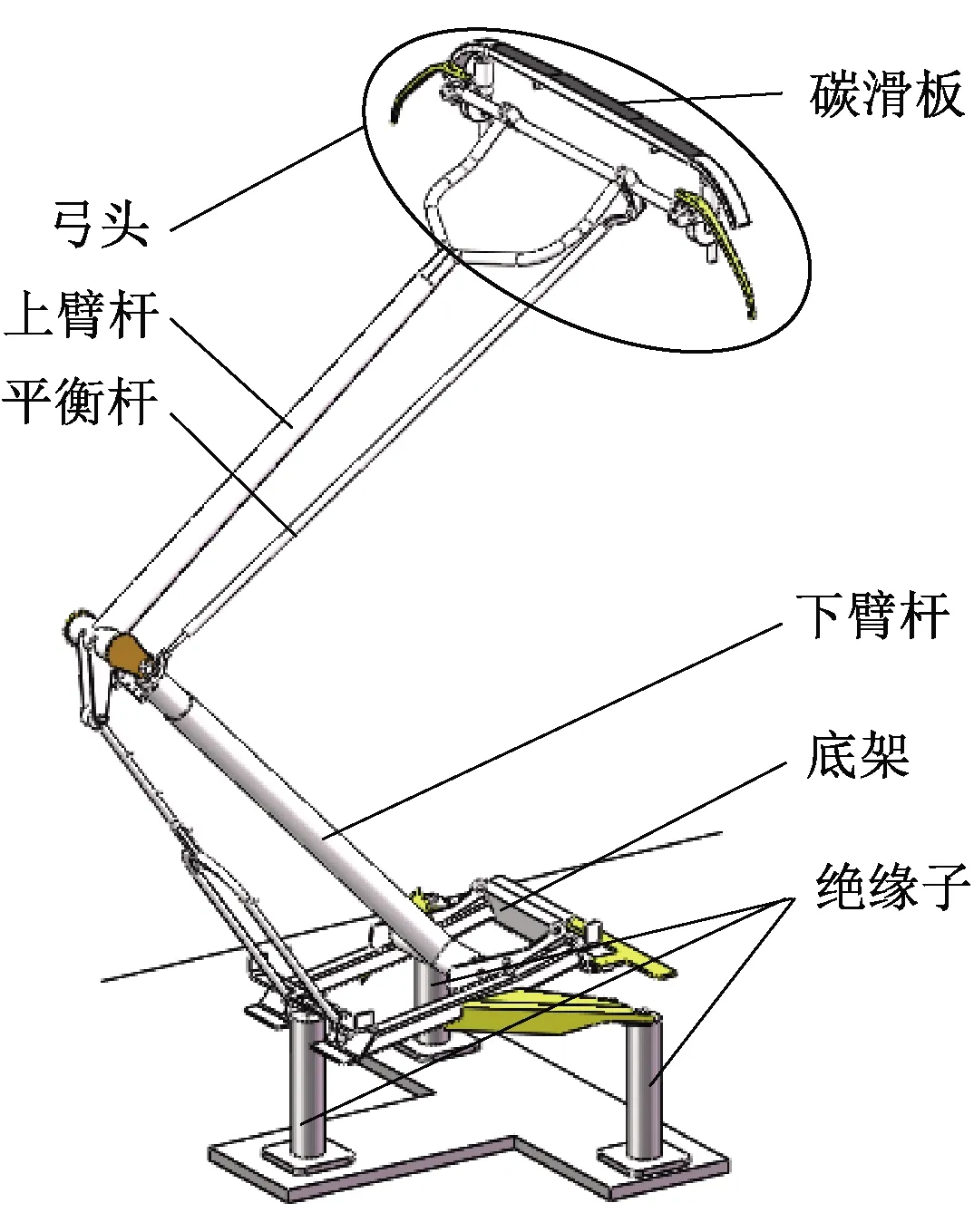
图2 受电弓简化模型
1.2 网格划分
1.2.1 计算域及边界条件设置
首先确定外部流场的计算域,设定的计算域既要尽量减小对受电弓周围湍流流场的影响,又不能超过已有计算机的计算能力。综合考虑,设定外流场为长250 m、宽66 m、高50 m的长方体,流场入口距车头40.5 m,流场出口距车尾130 m,列车位于中轴线上并紧靠地面。设定的计算域如图3所示。
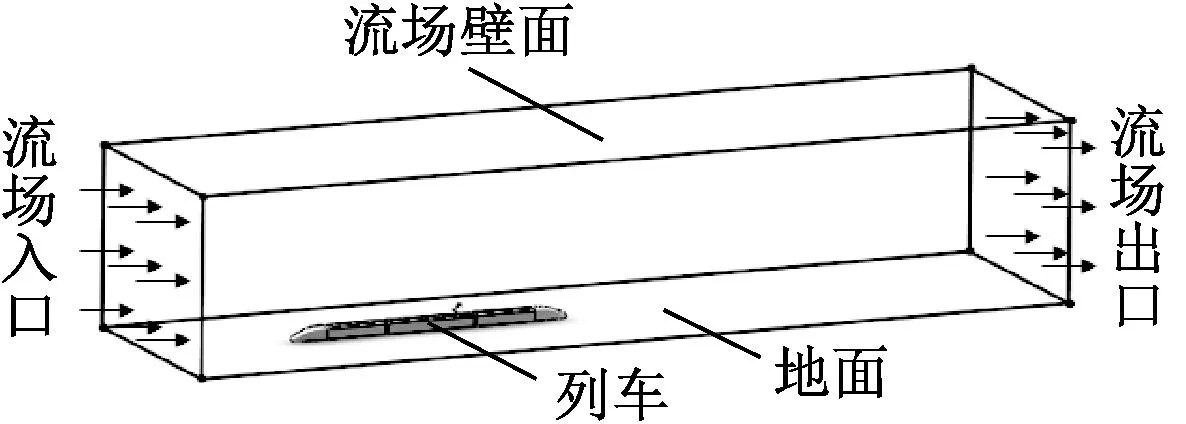
图3 计算域设置
为减小地面对流场的影响,地面边界条件为滑移壁面,移动速度和车速相同;复兴号高速列车最高速度Vmax为400 km/h(0.33马赫),已达到亚声速可压缩气流的临界值(0.3≤Ma≤0.8)[19],因此流场入口设置为质量流量入口(可压缩)。本文对受电弓在300、350、400、450 km/h(450 km/h为预测速度)4个运行速度下的噪声情况进行分析对比,对应的入口质量流量分别为3.37×105、3.93×105、4.49×105、5.05×105kg/s,所有边界条件的设置见表1。
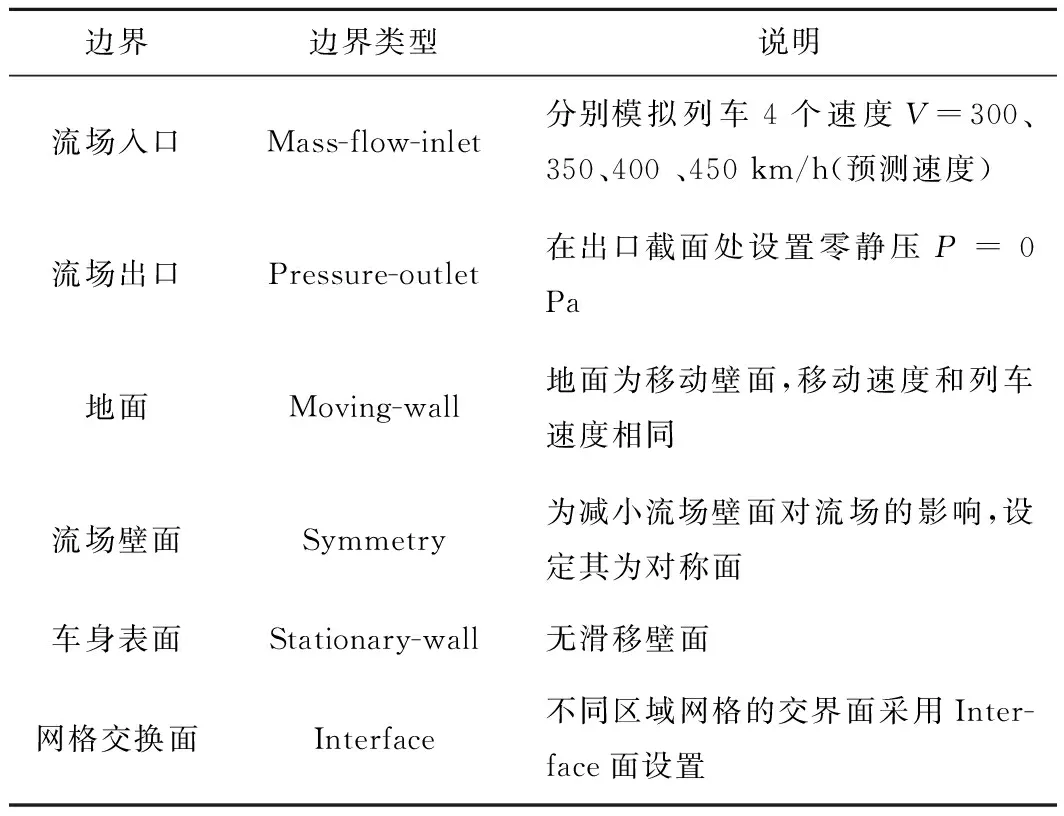
表1 边界条件设置
1.2.2 网格独立性检验
采用ICEM CFD软件对整车进行网格划分。对车体附近、受电弓附近及其尾部区域等湍流较强区域进行网格加密处理,如图4所示。由于固体近壁面的空气流动速度梯度较大,因此在整车表面设定边界层,边界层厚度为0.1 mm,层数为5层,增长率为1.1。
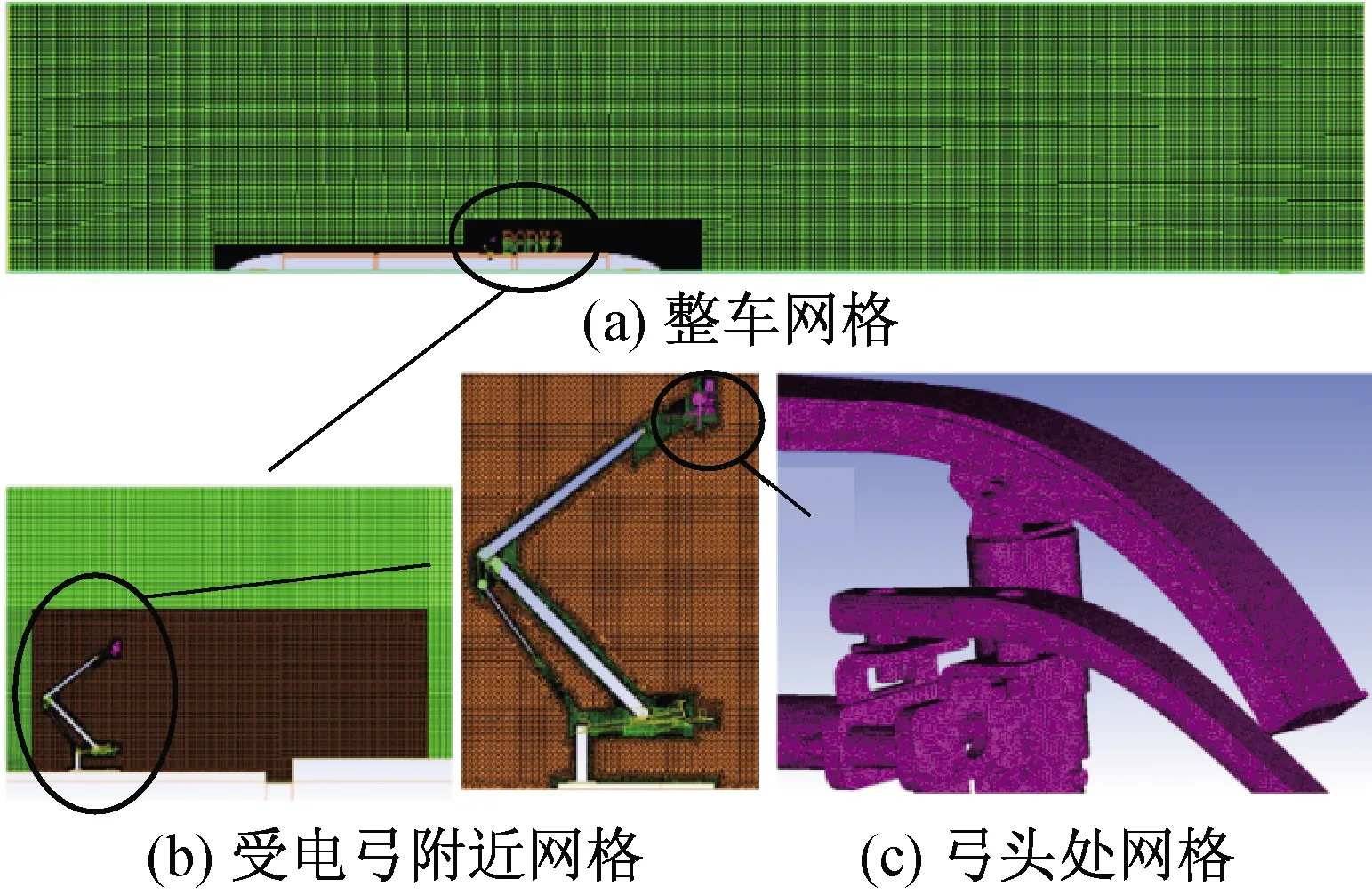
图4 整车网格划分
为尽量减小网格数对仿真结果的影响,进行网格独立性检验,划分5组密度不同的网格并在速度350 km/h下分别对受电弓表面的最大声功率级进行分析,分析结果见表2。

表2 网格独立性检验
由表2可知,从第4套网格开始受电弓最大声功率级变化趋于平缓,因此本文采用网格总数为2 866万的第4套网格进行数值模拟,其中受电弓附近及尾部网格数为1 814.40万,整车网格划分如图4所示。
2 受电弓外部流场特性分析
2.1 计算方法
本文采用以Navier-Stokes方程为基础的RNGk-ε模型对受电弓外部流场特性进行分析。相较于标准k-ε模型,该模型的ε方程有一个附加项,计算列车近壁面大速度梯度流场时更精确,控制方程如下:
k项
Gk+Gb-ρε-YM+Sk
( 1 )
ε项
( 2 )
式中:ρ为流体密度;xi和xj分别为i、j方向的位移分量;vi为i方向的速度分量;μeff为考虑了湍流黏度的总黏度;αk、αε为有效普朗特数的倒数,高雷诺数条件下,αk=αε≈1.393;C1ε=1.42;C2ε=1.68;C3ε、Sk和Sε均为自定义源项;Gk、Gb分别为速度梯度变化、浮力导致的湍动能。
( 3 )
式中:ρ为流体密度;T为温度;gi为重力矢量的分量;μt为流体的黏度系数。
YM为可压缩流中脉动膨胀对总耗散率的贡献,其计算式为
YM=2ρεMa2
( 4 )
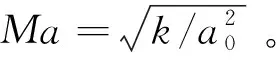
Rε为RNGk-ε相较于标准k-ε模型的附加项
( 5 )
式中:η=Sk/ε;η0=4.38;β=0.012;Cμ=0.084 5。
2.2 受电弓表面脉动压力分析
采用RNGk-ε模型分别对300、350、400、450 km/h速度下的高速列车受电弓表面脉动压力进行瞬态仿真模拟,由仿真结果可得,各个速度工况下的车身表面压力分布规律基本一致,主要是数值大小的差异。以列车速度350 km/h为例,受电弓表面压力分布如图5所示。

图5 受电弓表面压力分布云图
由图5可知,由于受到迎风气流的直接冲击,受电弓最大表面正压力出现在各杆件的迎风侧一面;最小表面负压力在各杆件和碳滑板表面的气流与固体壁面分离部位产生。不同速度下的最大正压与最小负压见表3。
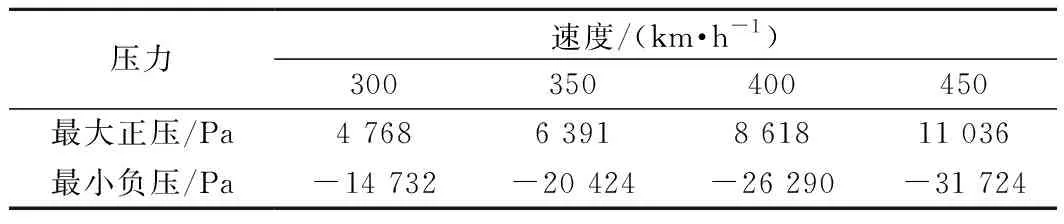
表3 不同速度下受电弓表面压力
由表3可知,随着速度的增加,受电弓表面最大正压力逐渐增大,最小负压力逐渐减小;表面最大正压与最小负压随着速度的增加都近似呈线性变化。
2.3 受电弓附近湍动能与涡量分布规律分析
以车速350 km/h为例,图6为受电弓纵向对称截面的湍动能分布云图,图7为采用Q基准(尺度为0.001 2)的受电弓附近涡量分布云图。
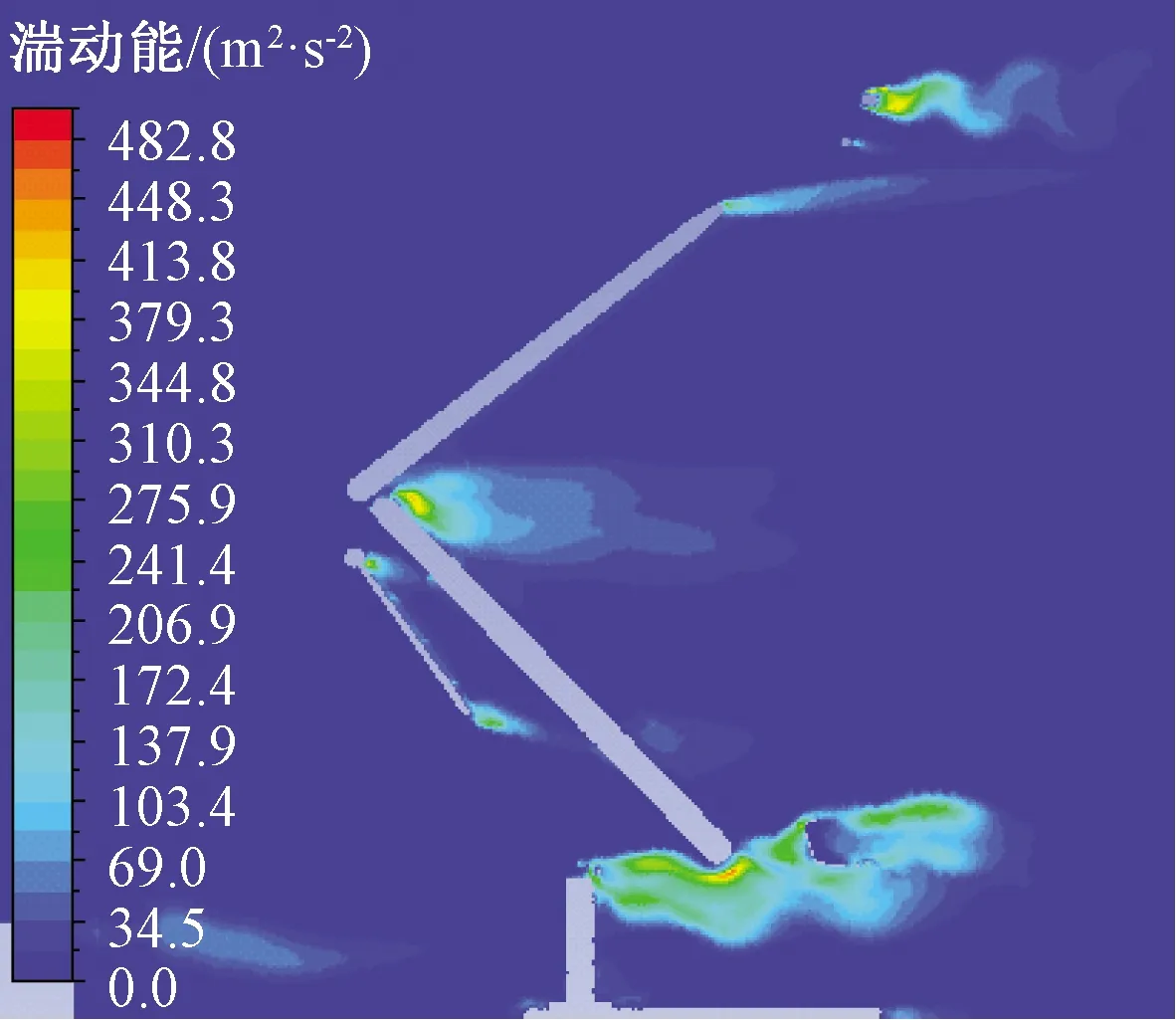
图6 受电弓截面湍动能分布云图
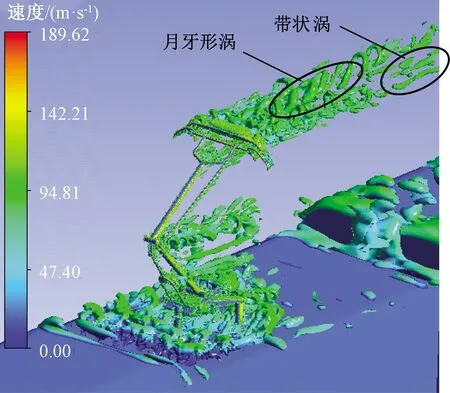
图7 受电弓附近涡量分布云图
综合分析图6、图7可知:
(1)高速气流流经受电弓各突出部位时受到阻碍向两侧排开并与壁面分离,在其尾部频繁产生涡脱落和重组现象,产生了较大的湍动能。
(2)涡脱落现象和较大湍动能发生位置主要在弓头、上下臂杆结合处和底架部位;最大湍动能为1 144.32 m2/s2(图6湍动能为0~500 m2/s2显示效果)。
(3)弓头的中间位置主要是月牙形涡,边缘部位主要为带状涡。
3 受电弓气动噪声特性分析
3.1 声源特性3.1.1 计算方法
利用以宽频带噪声源模型为基础的The Boundary Layer Noise Source Model计算受电弓气动噪声源,能够更好地处理高速列车受电弓湍流边界层产生的气动噪声对总声功率的局部贡献问题。由湍流边界层引起的远场声强为
( 6 )
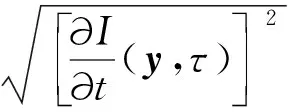
整个固体表面发出的声功率级可以表示为
( 7 )
式中:ρ0为静止介质的密度;I(y)为单位表面积对总声功率级的局部贡献,即
( 8 )
3.1.2 声源特性分析
在利用RNGk-ε湍流模型进行瞬态仿真的基础上,采用The Boundary Layer Noise Source Model,仿真得到300、350、400、450 km/h 4个速度下高速列车整车上表面及受电弓细节处的声功率级分布,结果如图8、图9所示。
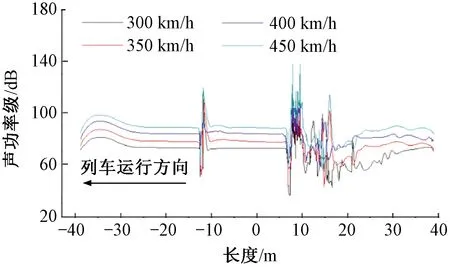
图8 列车上表面声功率级分布曲线
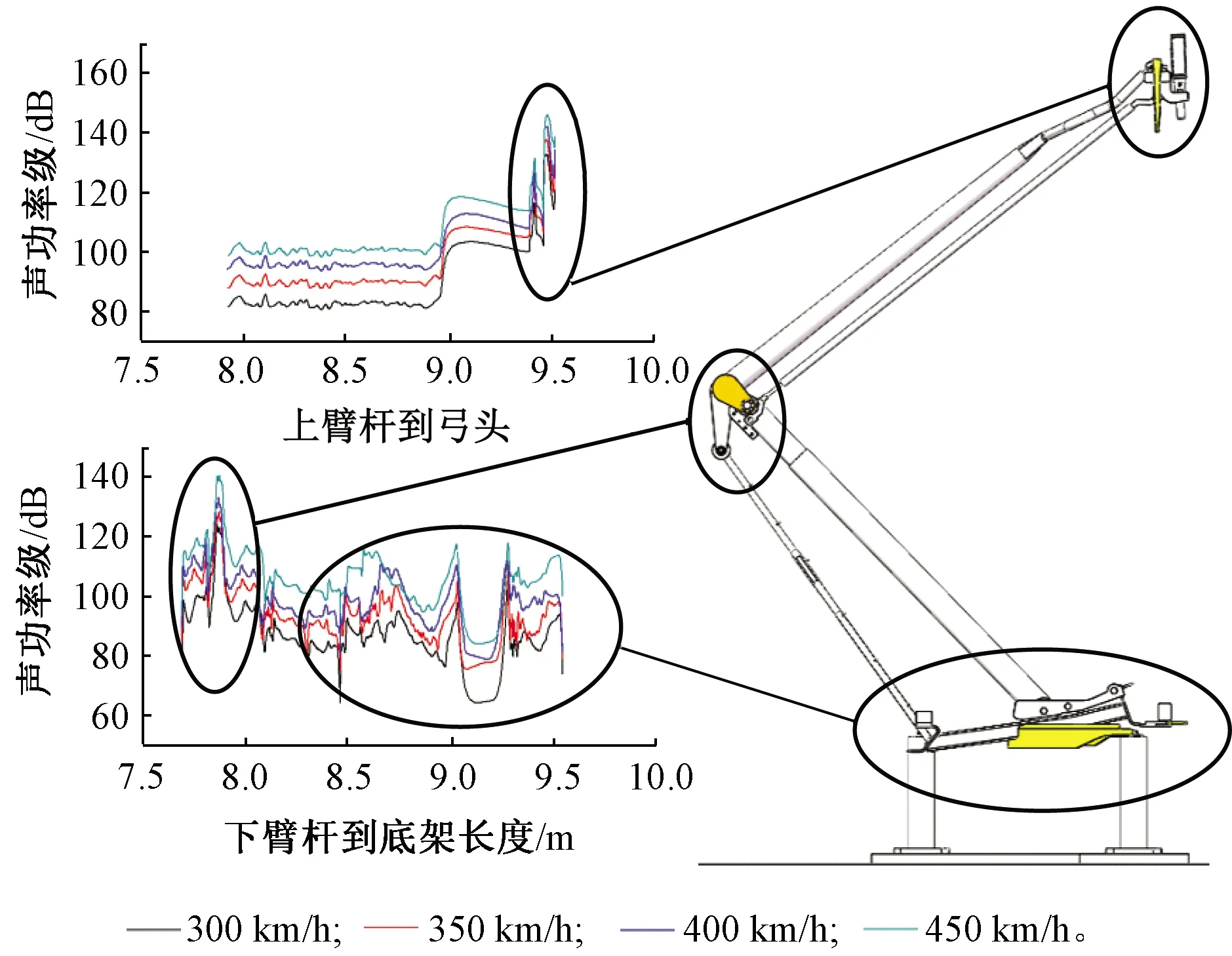
图9 受电弓处声功率级分布曲线
由图8、图9可知,整车的较大声功率级在车头中部、车厢结合处和受电弓部位产生,而最大声功率级在受电弓处产生;受电弓处较大的声功率级出现在弓头、上下臂杆结合处以及底架位置,而最大声功率级在弓头产生。在车速为350 km/h时,最大声功率级为137.79 dB。
图10为受电弓弓头弯角处以及上下臂杆结合处的声功率级分布与压力分布的对比。
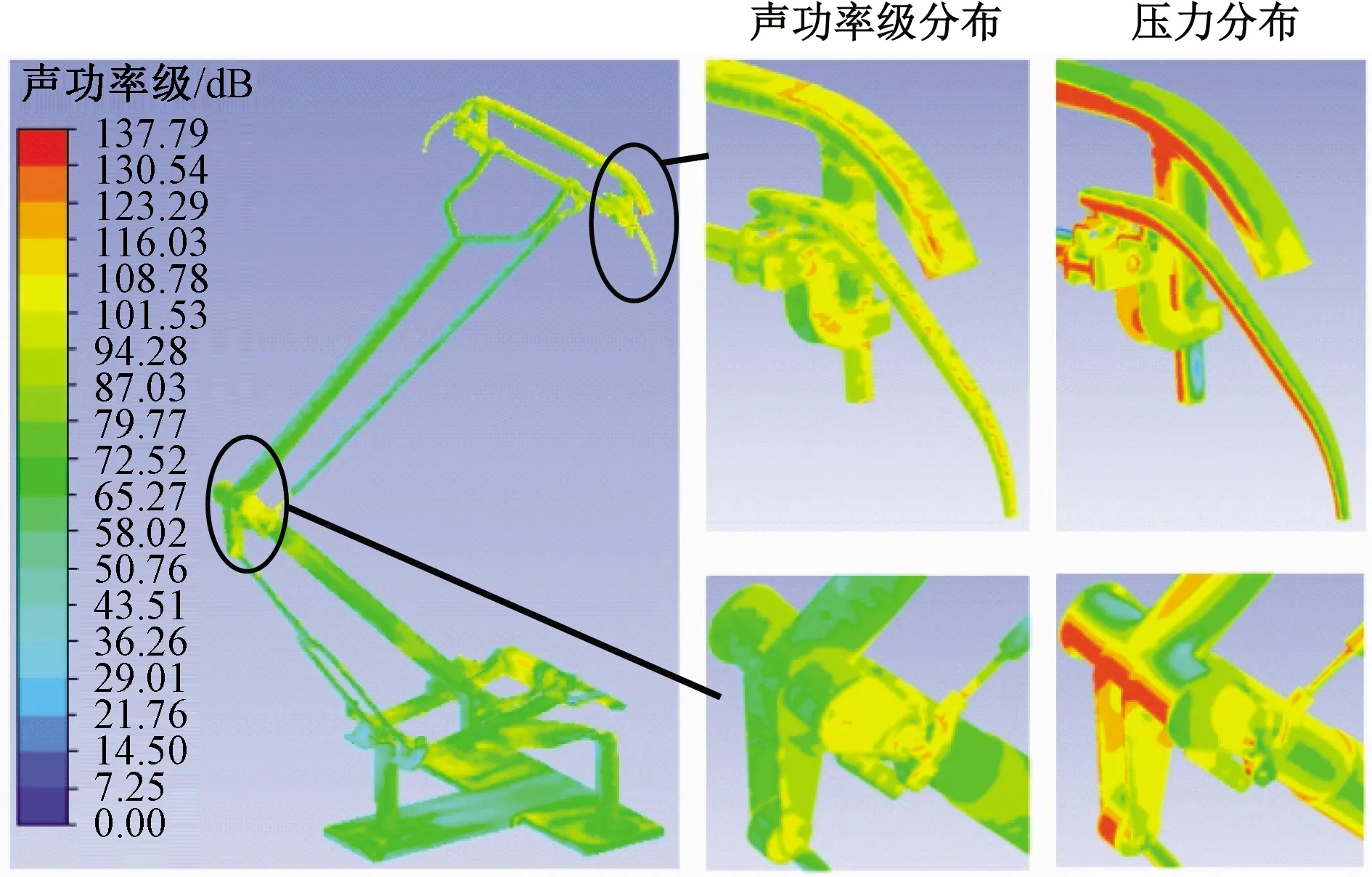
图10 受电弓处声功率级与压力对比云图
由图10可知,大部分声功率级的极大值点都在各部位负压极小值位置,而负压极小值位置都是气流与固体壁面的分离点,因此列车高速运行时气流遇到受电弓表面而发生分离的现象是受电弓气动噪声产生的主要原因之一。
3.2 远场气动噪声分布规律
3.2.1 计算方法
采用大涡模拟作为计算受电弓远场气动噪声的基础,大涡模拟法将大、小尺度涡分开计算,大尺度涡利用流体方程直接求得,小尺度涡则需附加一个亚格子模型求得。
( 9 )
(10)
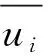
(11)
式中:Δ为网格尺寸;Cs=0.1(Smagorinsky常数)
以等效连续A计权声压级(LpAeq,T)评定受电弓远场气动噪声,由铁路噪声标准ISO 3095—2013定义,等效连续A计权声压级为[20]
(12)
式中:T为采样时间分辨率;pA(t)为非定常A计权声压;p0为基准声压,在空气中p0=2×105Pa。
噪声监测点的设置方式如图11所示。
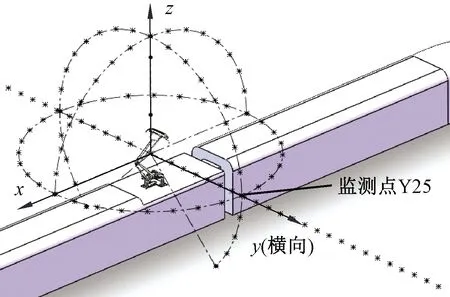
图11 远场气动噪声监测点分布
(1)以受电弓质心为原点,15 m为直径沿x-y(水平)面每两个监测点夹角11.25°设置一周噪声监测点,沿x-z(纵断)面每两个监测点夹角11.25°设置半周噪声监测点,沿y-z(横断)面每两个监测点夹角11.25°对称设置3/4周噪声监测点,总共61个噪声监测点。探究各个速度下受电弓沿各个方向噪声的传播规律。
(2)距受电弓质心1.6 m处为起点每隔1 m布置1个噪声监测点,在列车左右两侧对称布置23×2个噪声监测点(左侧省略表示),探究受电弓气动噪声随着离列车距离增加的衰减规律。
3.2.2 远场气动噪声沿各个方向传播规律
大多数噪声源具有指向性特点,即在离声源某一固定距离上,声源在不同方向上的辐射声压级一般不同[21]。为探究高速列车在运行时受电弓部位气动噪声沿各个方向的传播规律,选择水平面、横断面、纵断面3个平面探究监测点声压级的变化规律(图12)。

图12 受电弓远场气动噪声沿各个方向传播规律
(1)气动噪声指向特性:由图12(a)可知,水平面上4个速度下受电弓均在两侧(90°和270°左右)声压级达到最大值,并且有一定的对称性;在190°左右声压级达到最小值,因此列车运行时在水平方向上受电弓的左右两侧噪声比前后两侧噪声更大。由图12(b)可知,横断面上4个速度下受电弓均在最高位置(90°左右)声压级达到最大值,在左右的水平位置(0°和180°)声压级最小,因此列车运行时气动噪声对其上方(列车过站时在站台天桥上的行人)比对左右两侧行人的影响更大。由图12(c)可知,纵断面上4个速度下受电弓均在受电弓弓头指向的位置(70°~80°)噪声达到最大值,进一步说明弓头为较大的噪声贡献位置。
(2)衰减特性:水平面、横断面、纵断面3个平面内平均声压级随速度增加的变化规律分别为3.51→2.99→2.92 dBA、3.31→3.15→2.99 dBA、3.47→3.14→2.71 dBA,因此,列车低速运行时(Ma≤0.3、周围流场不可压缩),远场声压级随着速度增加,增长较快;列车在亚声速运行时(0.3≤Ma≤0.8、周围流场可压缩),远场声压级随着速度增加,增长较慢。
3.2.3 远场气动噪声与距离的传播关系
为了探究受电弓气动噪声随着传播距离增加的衰减规律,距受电弓质心1.6 m处为起点、23.6 m处为终点,每隔1 m左右对称布置23×2个噪声监测点,如图11所示。远场气动噪声随距离增加的变化规律如图13所示。
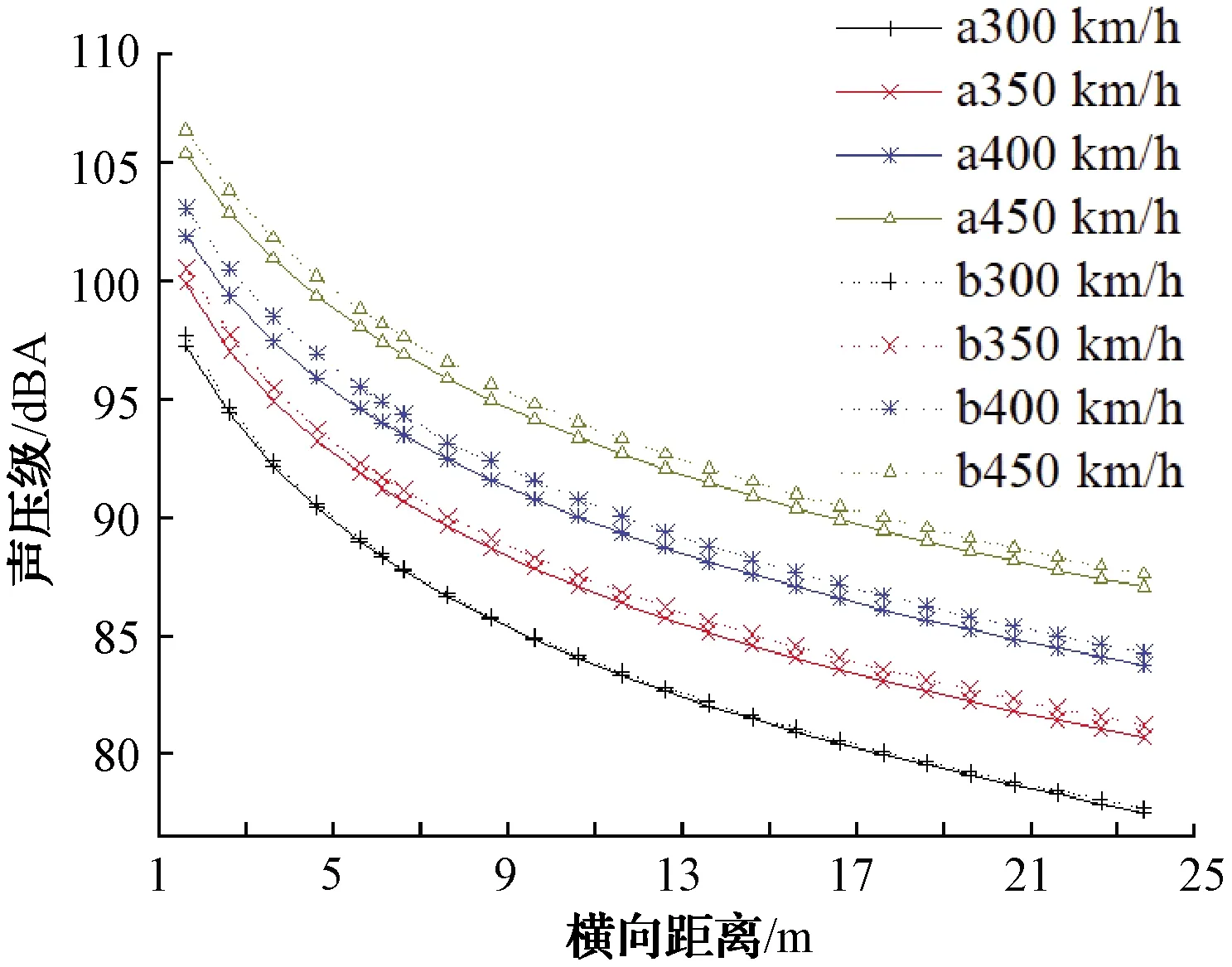
图13 受声点声压级随距离增加变化规律
由图13(a、b分别为受电弓左右两侧)可知,远场A计权声压级LA与传播距离的对数线性相关,满足以下函数关系
LA=algS+b
(13)
式中:S(1.6 m≤S≤23.6 m)为横向距离;a、b为常数。
4个速度下有平衡杆一侧(b侧)对应的表达式分别为
300 km/h:LA1=-17.82lgS+102.26
(14)
350 km/h:LA2=-17.32lgS+105.11
(15)
400 km/h:LA3=-17.22lgS+108.03
(16)
450 km/h:LA4=-17.17lgS+111.39
(17)
远场A计权声压级随传播距离的衰减特性:距离受电弓越远,其声压级衰减速度越缓慢;式(13)中常数a随着速度的增加越来越小,衰减值为-0.5→-0.1→-0.05,衰减速度越来越小,并最终趋于稳定值17.15左右;常数b随着速度的增加越来越大,每两个速度之间的增长值为2.85→2.92→3.36,增长速度越来越快。
3.2.4 远场气动噪声频域分布特性
为探究受电弓远场气动噪声的频域特性,以监测点Y25处(距受电弓7.5 m,图11)的宽频带噪声为研究对象,采用傅里叶变换(FFT),把监测点Y25处的声压级信号从时域转换到频域,分析300、350、400、450 km/h 4个速度下的频域分布特性,如图14所示。由图14 可知,7.5 m远处在不同速度下的气动噪声频域分布规律具有相似性,且都有着较宽的频率;4个速度下都在100~400 Hz声压级出现峰值。
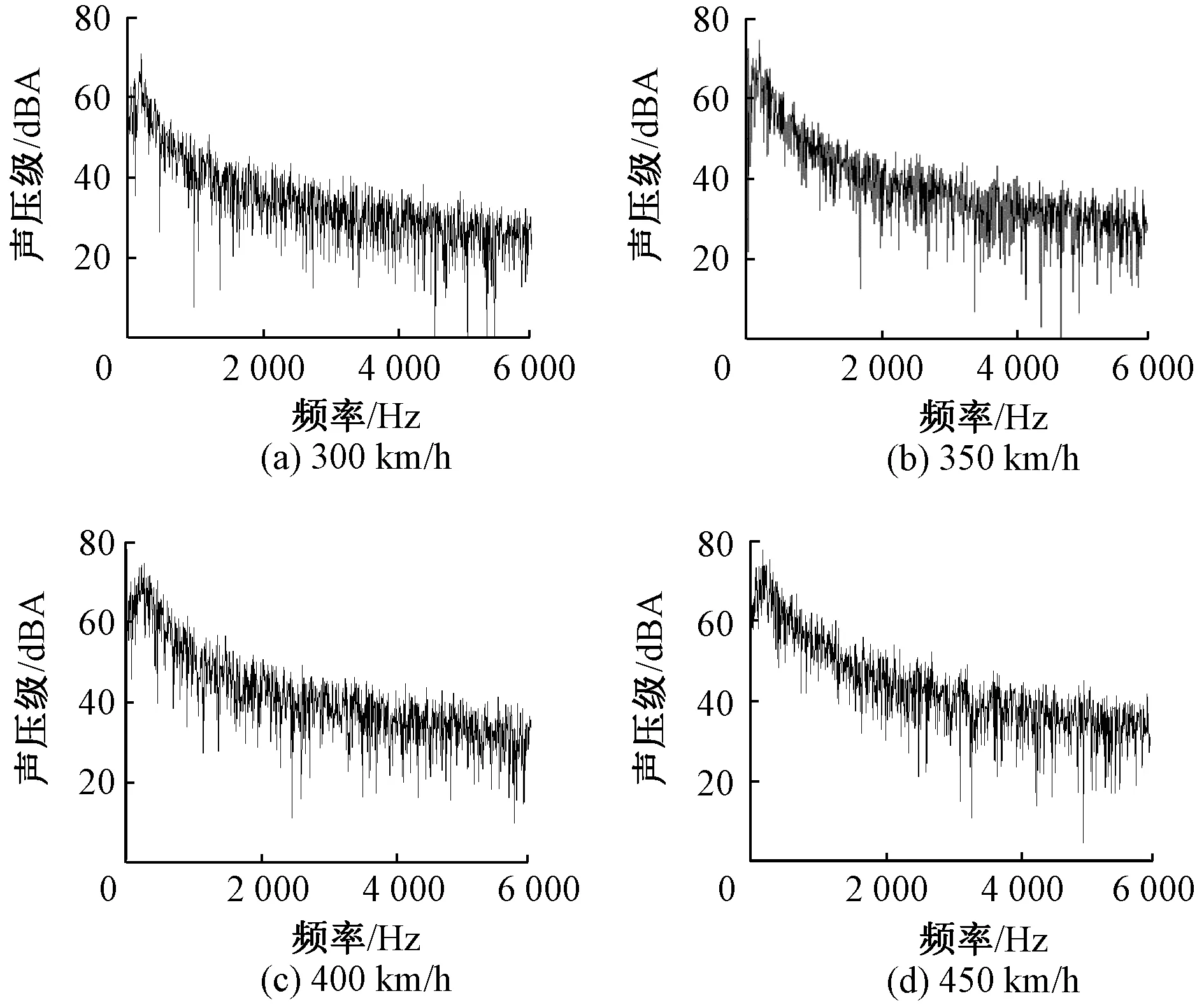
图14 监测点Y25处4个速度下声压级频谱
由于500~6 000 Hz的中频段是人最敏感的区域,且A计权声压级是模拟耳朵对55 dBA以下较低强度噪声的频率,与人耳的听感特性最为相似贴切[22]。因此,采用1/3 倍频程对高速列车宽频带气动噪声A 计权声压级进行频域分布分析。
图15为列车各个速度下监测点Y25处的A计权声压级的1/3倍频谱图,由图15可知:
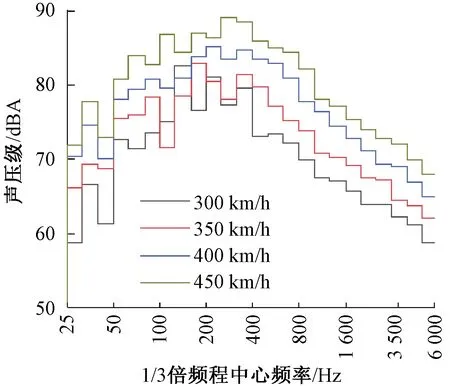
图15 监测点Y25处四个速度下1/3倍频谱
(1)随着列车运行速度的增加,A计权声压级越来越大,能量主要集中在25~6 000 Hz频率范围。
(2)4个速度下,A计权声压级都是从25 Hz开始迅速提高,到145~315 Hz达到顶峰;然后迅速衰减到1 000 Hz;从1 000 Hz到6 000 Hz为缓慢衰减期,且这阶段气动噪声频率的对数lgf与声压级近似成线性关系。
(3)列车速度为300、350、400、450 km/h时,主频分别在145~160、165~200、195~230、250~315 Hz之间,随着列车速度的增加,主频从低频缓慢移向高频。
4 受电弓弓头仿生降噪分析
4.1 弓头仿生结构优化设计
根据GB 12525—1990《铁路边界噪声限值及其测量方法》[23],距铁路外侧轨道中心线30 m处,既有铁路无论昼夜噪声限值都为70 dBA,新建铁路昼夜噪声限值分别为70、60 dBA。以350 km/h列车运行速度为例,根据3.2节的计算,在30 m处受电弓的远场气动噪声声压级为79.43 dBA,因此对受电弓的气动降噪迫在眉睫。
针对受电弓最大噪声贡献部位弓头,基于鸮翅膀低噪声飞行机理[24],在不影响弓网接触稳定性并考虑列车双向运行特点的前提下,低噪声弓头须设计成前后对称结构且碳滑板上表面几何形状不变。因此将鸮翅膀的前端凸起和尾部梳状低噪声生态学特征(图16)结合成前后对称椭球状凸起结构应用到弓头较大噪声贡献部位。

图16 鸮翅膀低噪声生态学特征
基于多目标优化法则,对图17所示的碳滑板和圆杆进行仿生优化设计。在碳滑板和圆杆上施加前后对称椭球状凸起结构,对最优凸起高度进行探究。对碳滑板和圆杆凸起高度分别为18~72、1.5~55.5 mm的38组数据(每隔1.5 mm一组,原始弓头为第一组),在监测点Y25、运行速度为350 km/h下的弓头截面远场声压级进行二维数值模拟分析,探究最优凸起高度。
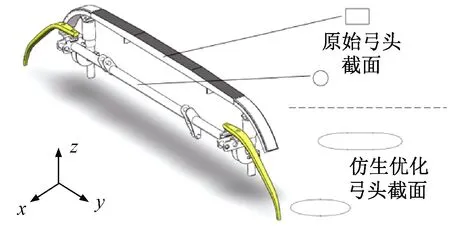
图17 弓头及椭球状凸起结构特征
图18分别为第1、8、22、30、34、38组(受篇幅限制只列出6组)优化前后弓头截面湍流状态图;图19为监测点Y25处声压级随凸起高度增加的变化规律。由图18、图19可得:
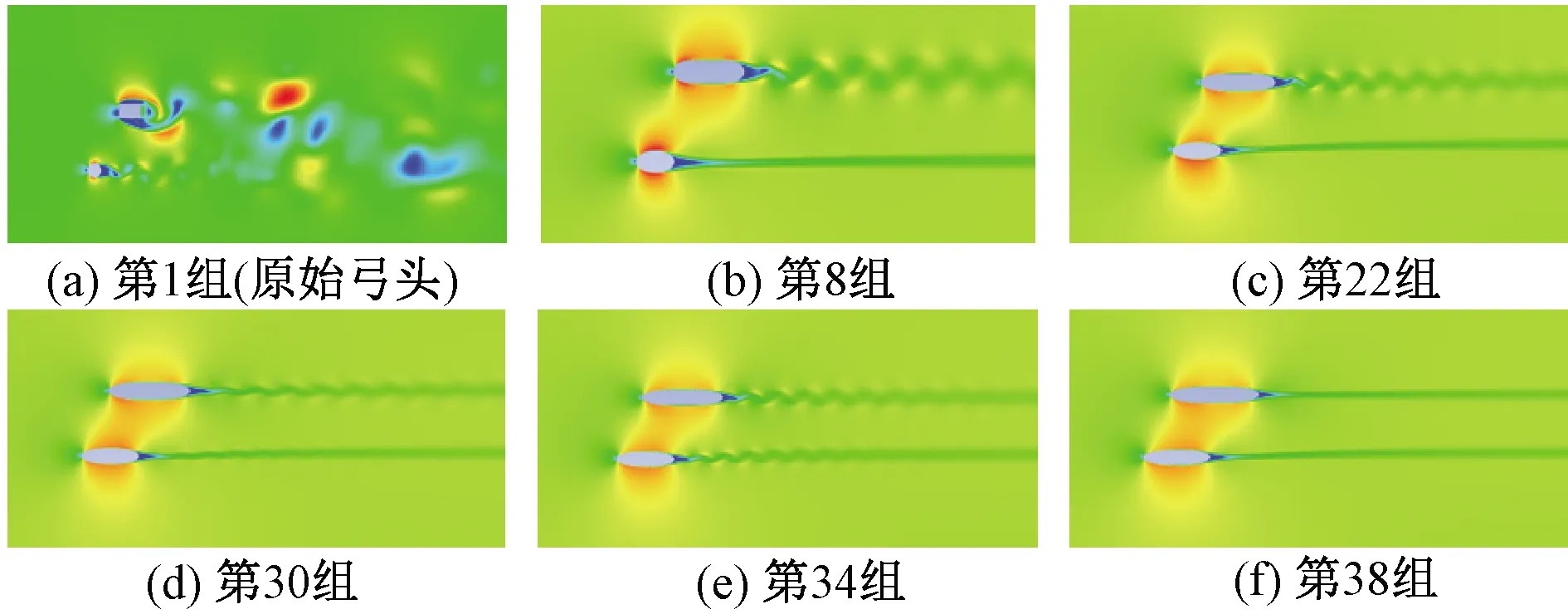
图18 原始弓头和仿生优化弓头截面湍流状态
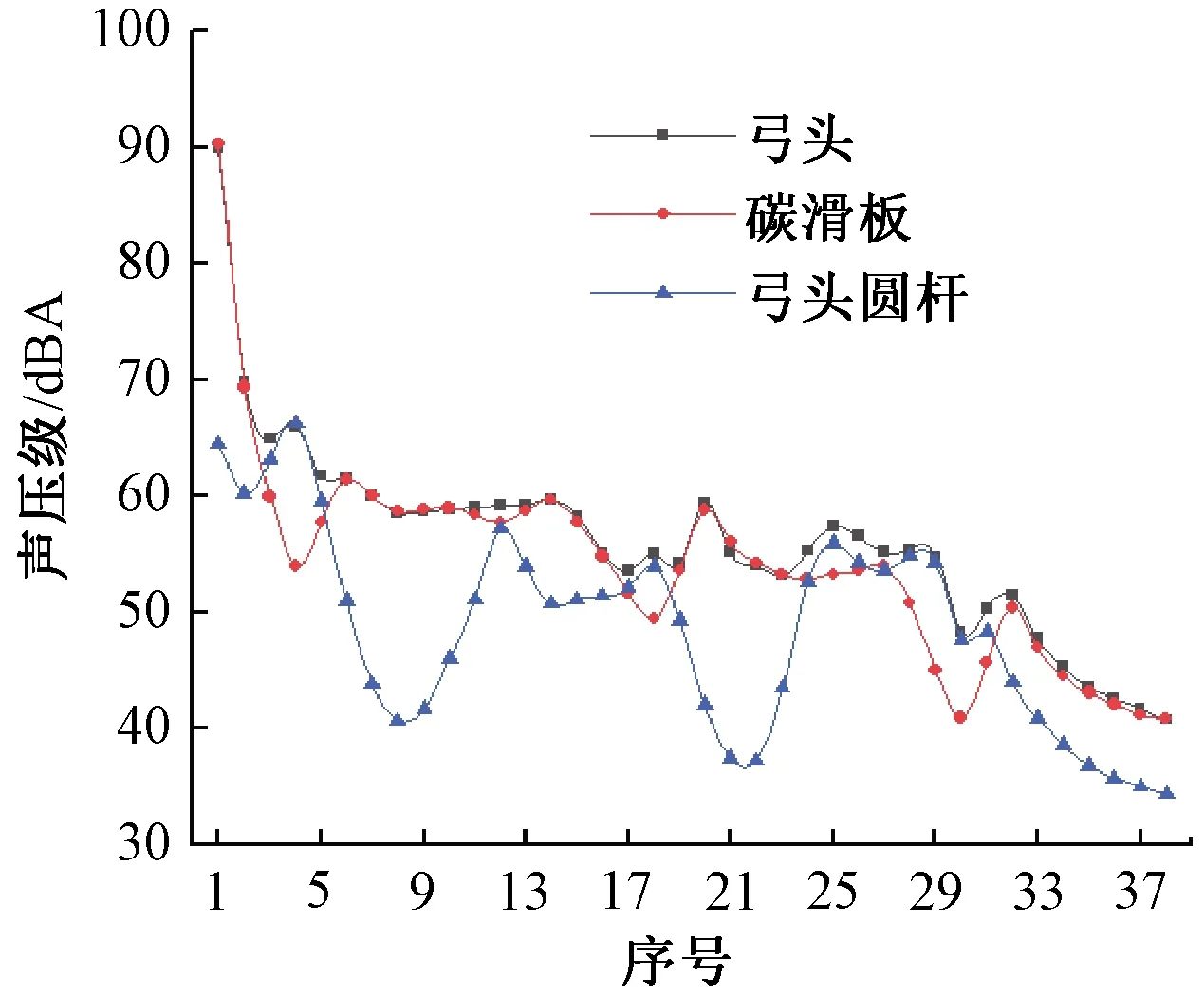
图19 远场声压级随凸起高度变化规律
(1)对比观察速度云图和声压级随凸起高度变化规律图可知,尾部湍流越弱,噪声越小。
(2)在碳滑板凸起高度分别为21、42、60 mm时,有3个极小值点;在圆杆凸起高度为10.5、31.5 mm时,有两个极小值点,且随着凸起高度的增加,远场噪声呈现波动性减小。
(3)总噪声与碳滑板和圆杆两者的较大噪声值极为相近,说明控制物体的较大噪声发生位置对控制总噪声起到了极为关键的作用。
综合考虑降噪效果、经济效益和安全效益(声压级越低降噪效果越好,凸起高度越少成本越低、对弓网接触稳定性影响越弱),选择碳滑板凸起高度为21、42、60、72 mm,圆杆凸起高度为10.5、31.5、55.5 mm进行4×3的多变量实验分析,探究两者相互影响下的各自最佳凸起高度,见表4。
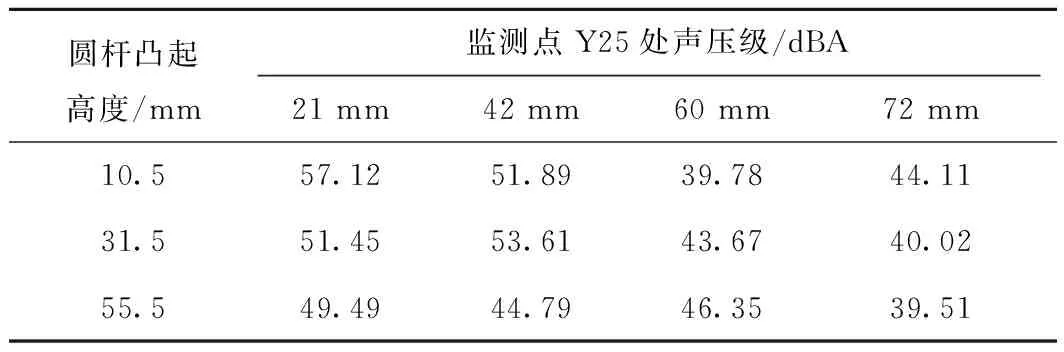
表4 多变量实验分析
由表4可知,第(1,3)、(2,4)、(3,4)组的实验弓头总噪声都控制在最小值40 dBA左右,因此选择三组中凸起高度最小的第(1,3)组(碳滑板凸起高度为60 mm,圆杆凸起高度为10.5 mm)作为优化指标。
4.2 仿生优化设计降噪效果分析
在4.1节研究结果的基础上,确定碳滑板凸起高度为60 mm,圆杆凸起高度为10.5 mm,建立弓头仿生优化后的整车气动噪声三维分析模型,弓头处如图20所示。
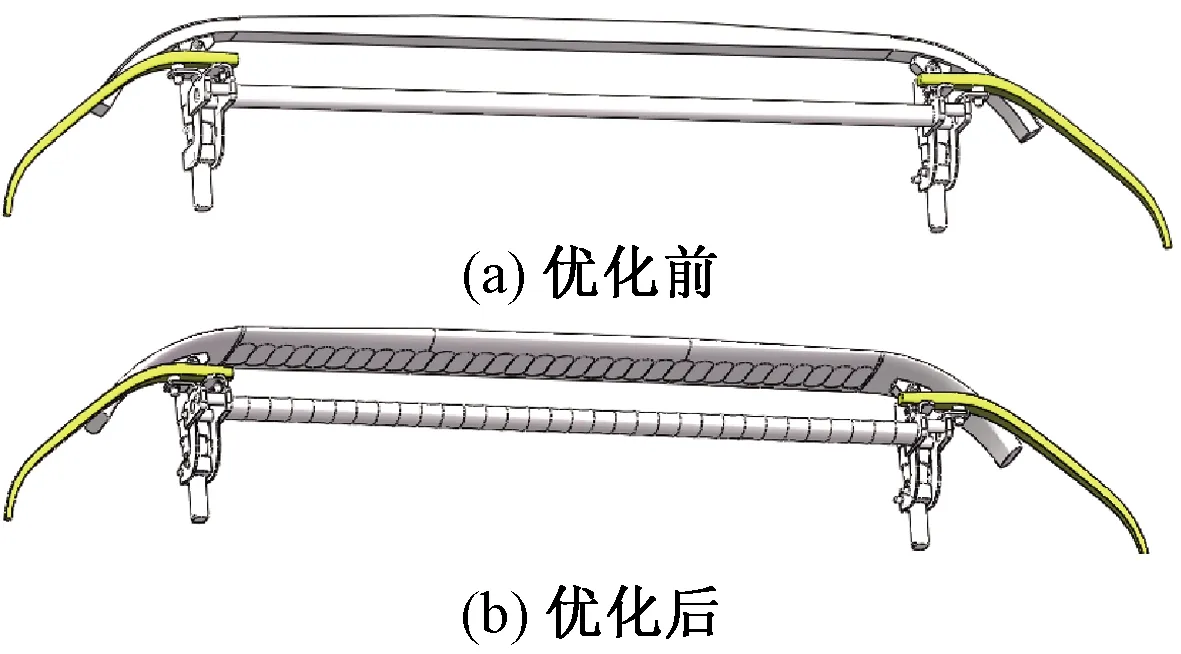
图20 仿生优化前后弓头处对比
对比优化前后的受电弓涡量状态,可以得出优化后受电弓的尾涡脱落得到了明显的抑制,特别是碳滑板中间的月牙形涡大幅减少(图21)。
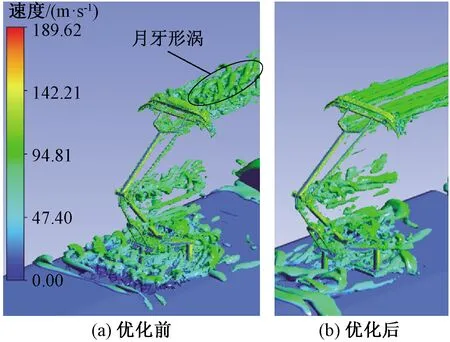
图21 受电弓仿生优化前后涡量对比
图22为运行速度350 km/h时,距铁路外侧轨道中心线30 m处仿生优化前后受电弓A计权声压级的1/3倍频谱对比。
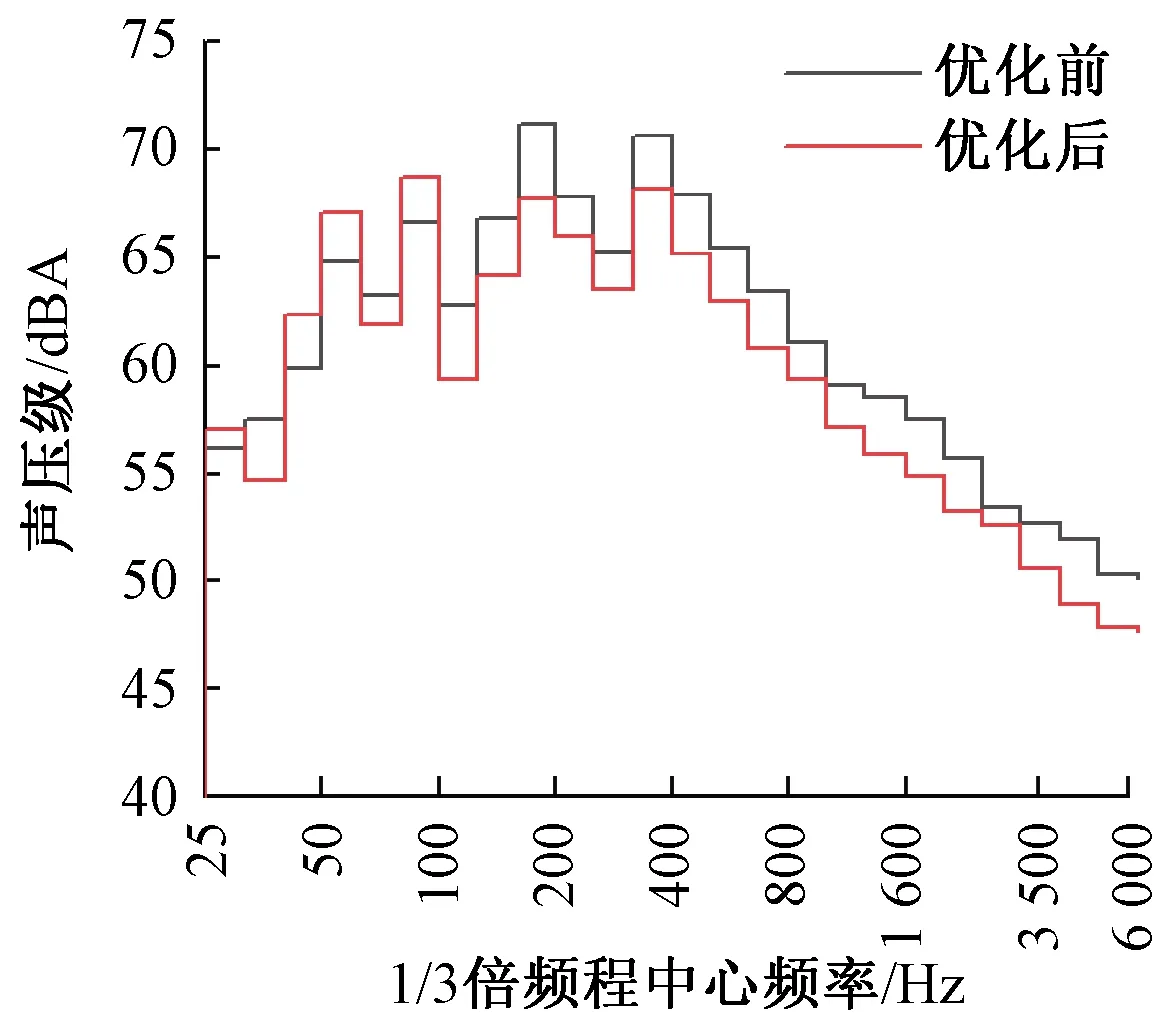
图22 30 m远处仿生优化前后1/3倍频谱
对比分析仿生前后的噪声频域分布,可得:
(1)在100~6 000 Hz范围内,各个频段声压级普遍减弱2~3 dBA。
(2)最大主频由优化前的190 Hz左右移动到了80 Hz左右,主频向低频移动。
(3)优化前受电弓在距铁路外侧轨道中心线30 m处总声压级为79.43 dBA,优化后相同位置总声压级减少了2.49 dBA,值为76.94 dBA。
4.3 仿生优化设计可行性分析
仿生优化后受电弓弓头碳滑板的质量m从3.46 kg变为4.17 kg,外形结构也发生了变化,因此会引起气动特性及其固有频率的改变,须对弓头所受的气动力进行分析,并判断是否会产生涡激共振现象[25]。
对运行速度350 km/h时由气动力作用的碳滑板上下表面脉动压力差时域分布规律和碳滑板气动阻力进行分析见表5、图23。由表5和图23可得:

表5 气动阻力与脉动压差分析
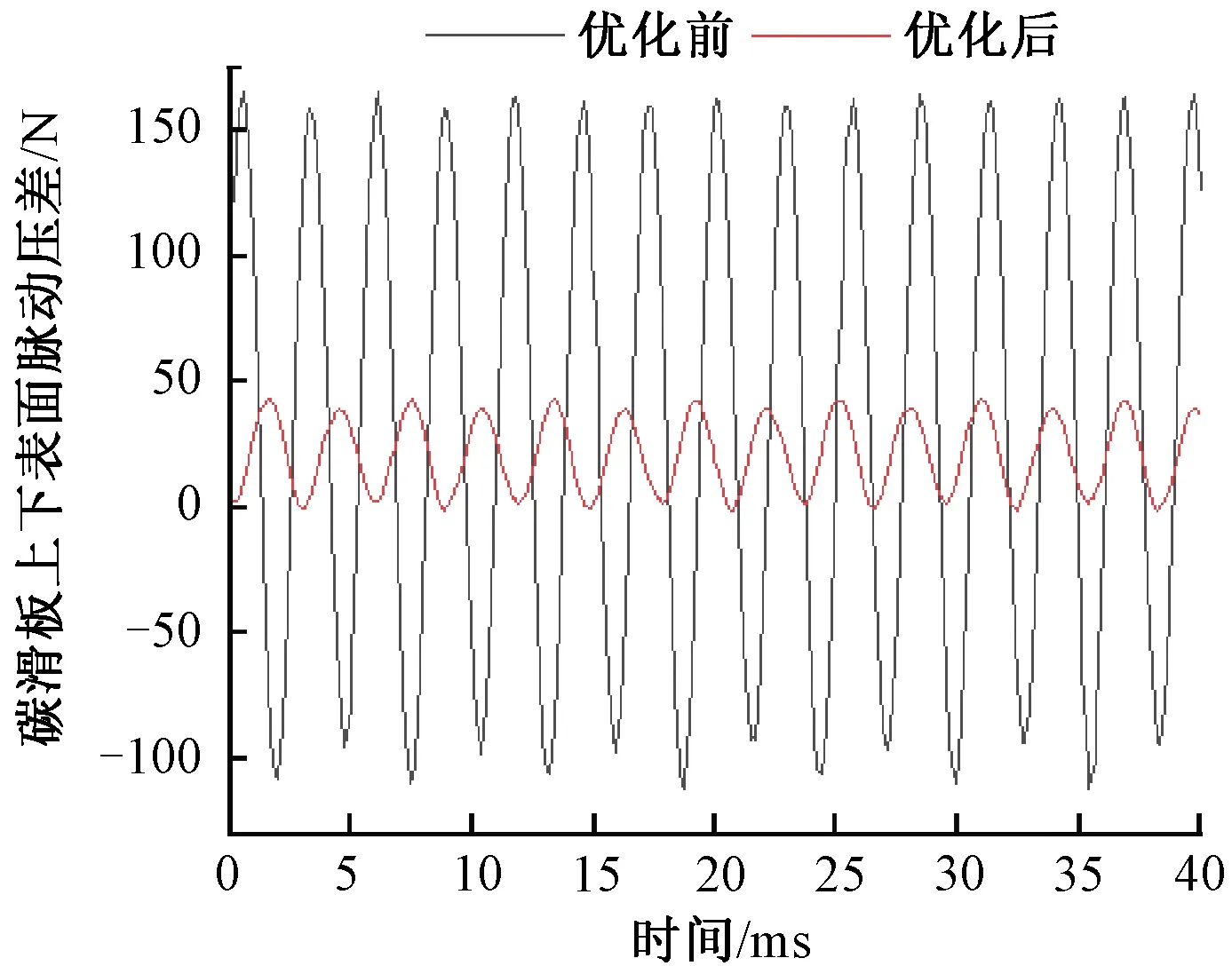
图23 脉动压差时域分布
仿生优化后碳滑板气动阻力减小了433.31 N;碳滑板上下表面脉动压差频率(涡激振动频率)基本相近,脉动压差最大幅值有115 N左右的明显减小。
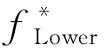
(18)
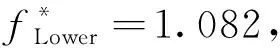
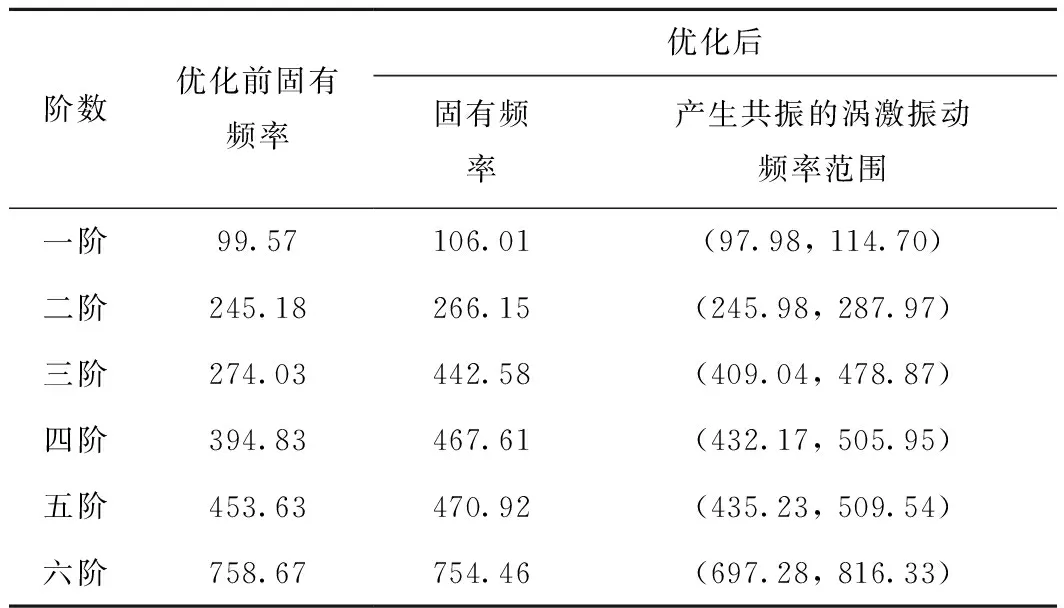
表6 弓头碳滑板优化后前六阶固有频率 Hz
由表6、表7和图24可得:

图24 弓头碳滑板优化前后模态振型的对比
(1)优化前后碳滑板在一、二、五、六阶固有频率基本相近,三、四阶固有频率分别有168.55、72.78 Hz的增加。
(2)碳滑板在四阶振型上由优化前的扭转振动变为弯扭结合振动,在五阶振型上由优化前的弯曲振动变为扭转振动。
(3)优化后的碳滑板涡激振动频率为353 Hz,介于二阶和三阶固有频率之间,但是并未处在产生共振的频率范围(245.98, 287.97)Hz和(409.04, 478.87)Hz内,因此仿生优化后的受电弓碳滑板在列车运行速度为350 km/h时不会产生涡激共振现象,不影响弓网接触稳定性。
5 结论
(1) 受电弓气动噪声源特性。高速列车整车的较大噪声位置出现在车头中部、车厢结合处和受电弓部位,其中受电弓部位最大,最大声功率级为137.79 dB (速度350 km/h);受电弓各部位噪声的大小弓头>上下臂杆结合处>底架>其他位置。
(2) 受电弓远场气动噪声指向特性。4个速度下远场气动噪声指向规律基本相同。受电弓各方向上噪声大小排列:受电弓质心指向弓头方向>正上方>左右两侧>正后方>正前方。因此,列车过站时车站天桥上的乘客受到气动噪声的影响比两侧站台候车乘客受到的影响更大。
(3) 受电弓远场气动噪声传播规律。距离受电弓越远,远场A计权声压级衰减速度越缓慢,与传播距离的对数之间线性相关。
(4) 宽频带噪声频域分布规律。受电弓远场气动噪声有较宽的频域分布,4个速度下主频都在145~315 Hz之间;A计权声压级都是从25 Hz开始迅速提高,到145~315 Hz达到顶峰,然后迅速衰减到1 000 Hz左右,1 000~6 000 Hz是缓慢衰减期,这阶段频率的对数lgf与声压级近似成线性关系;随着列车速度增加,主频从低频缓慢移向高频。
(5) 受电弓弓头仿生降噪效果。当碳滑板凸起高度为60 mm,圆杆凸起高度为10.5 mm时,弓头的气动噪声最小。仿生优化后受电弓气动噪声在距铁路外侧轨道中心线30 m处为76.94 dBA,比优化前降低了2.49 dBA,降噪效果较为明显,并且宽频带噪声有向低频移动的趋势。后续将针对受电弓其他噪声贡献量较大部位的降噪方法展开深入研究。
仿生优化后的受电弓碳滑板涡激振动频率并未处在产生共振效应的频率范围内,不会产生涡激共振现象,且碳滑板的气动阻力减小了433.31 N,脉动压差最大幅值减小了115 N左右,对弓网接触稳定性具有一定的改善作用。

