基于改进Canny算子的输电导线图像边缘检测
李 磊,李英娜,2,赵振刚,2
(1. 昆明理工大学 信息工程与自动化学院,云南 昆明 650500;2. 云南省计算机技术运用重点实验室,云南 昆明 650500)
0 引言
输电导线是电网系统的重要组成部分,定期检修工作是保障电网工程质量的重要手段。在早期的巡线过程中,巡检人员需要通过目测的方式检查线路是否存在损坏现象。这种巡线方式存在以下问题:一方面,由于误判、漏查等原因,完整、准确的输电线路状况信息无法获得;另一方面,由于人工巡视的效率远远小于电网铺设效率,而且部分电网建设在偏僻、环境复杂的地区,对巡线人员的安全造成威胁。因此该方法不能满足日益庞大的电能组网巡检需求。
近年来,科研工作者将图像处理技术应用到输电导线的巡检工作中。利用计算机视觉技术,对巡线机器人、无人机等设备拍摄出的真实、完整的输电线路图片进行目标识别与提取是目前新兴的研究方向。文献[1]提出了一种改进的Freeman 链码表示法以实现输电导线图像提取。该方法有效地剔除了背景信息,对缺损部分进行补充拟合,但是准确度不高。文献[2]使用改进k-means与形态学处理相结合的方式提取导线图像,虽提高了效率,但是提取出的导线图像缺损和不连贯现象较严重。文献[3]综合利用颜色特征对导线进行识别。该方法对颜色敏感,故针对对比度低的图像不能达到很好的提取效果。文献[4]用一种改进的随机 Hough变换的方式提取导线图像。该方法需要人为设置和调试参数,过程繁琐且容易出现结果不准确的问题。
传统Canny边缘检测算子由于具有准确度高的优点而被广泛应用于图像边缘检测研究中。文献[5]使用选择性平滑滤波算法对传统Canny算法中的高斯滤波进行改进,解决了孤立边缘被过滤的问题。文献[6]通过引入小波变换增强方法进一步提高了Canny边缘检测的准确性。文献[7]使用中值混合滤波的方法去噪,降低了噪声干扰,使检测后的图片更清晰。
以上算法虽然进一步提高了图像边缘检测的精度,但是存在阈值选取局限性的问题,在阈值选取时需要人工迭代或根据经验选择合适的阈值。为了提高阈值选取的自适应性,本文引入了最大类间方差法[8](Otsu法)并对其进行改进。国内外研究学者已经使用了遗传算法[9-11]、粒子群算法[12-14]对传统Otsu算法改进,提高了Otsu法的计算效率和检测准确性;但是以上算法在搜索全局最优值的过程中表现不佳,容易局限在局部最优值中,影响边缘检测效果。
针对以上问题,本文使用了一种改进的Canny算子对架空输电导线图像进行识别。该算法通过改进的4方向梯度模板计算梯度值,并且使用结合截距法和人工蜂群算法的最大类间方差法以便自适应选取全局最佳阈值,目标是提高边缘检测的降噪水平,连贯、清晰、准确地提取导线的边缘信息,并且减少了人工干预,使自适应性获得增强。
1 传统Canny边缘检测方法
Canny边缘检测[15]已经广泛应用于计算机视觉领域的各个方向。传统Canny边缘检测步骤如下:
步骤1:利用高斯滤波,使图像中灰度变化剧烈的部分变平滑。高斯核函数为:
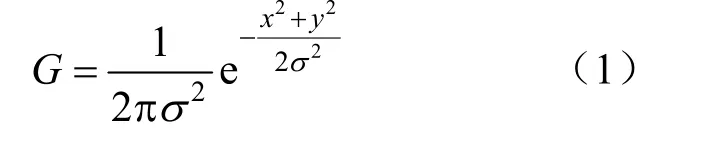
式中:σ为高斯核函数的标准差,该值越大,图像平滑效果越清晰。
步骤2:进行图像增强,图像中的部分像素点之间具有较强的差值,因此能够利用导数的特殊性,进行一阶有限差分计算,计算出各个像素点的梯度值和梯度方向,计算公式如式(2)(3)所示。

步骤3:利用非极大值抑制,保留具有相同梯度方向的像素点之间的最大值,消除图像增强过后的离散值,进一步提高图像的清晰度。
步骤4:应用双阈值检测筛查目前通过卷积取得的像素点是否属于边缘部分。设置低阈值θ1和高阈值θ2,判断每个像素点的灰度梯度与θ1、θ2之间的大小关系,其选择策略如表1所示。

表1 双阈值选择策略Tab. 1 Dual-threshold selection strategy
传统Canny算子存在方向模板和阈值选取的局限性问题。
(1)方向模板局限性问题[7]。架空输电导线由于受自身重力和外界自然气象(风力、温度)的影响会形成一定的弧垂。弧垂是指具有一定距离的相邻两个杆塔之间的导线在杆塔上悬挂点和导线最低点的垂直距离[16]。因此,导线一般呈抛物线状。传统的Canny算子检测的方向模板仅由水平和垂直2个方向确定,会丢失导线弯曲部分的边缘轮廓信息,因此具有一定的局限性。
(2)阈值选取局限性问题[17]。传统 Canny检测算法中双阈值检测的高低阈值选取是固定值或者是人工根据经验进行迭代选择,一般低阈值选取50,高阈值选取100。由于不同图像的亮度、对比度等参数不同,该选取策略不适用于对多种图片使用同一种双阈值进行分割的情形。另外,对每一张图片进行人工阈值选择,耗时费力,降低了图片分割的效率。
2 改进Canny算子的边缘检测
2.1 算法流程
改进的Canny算法过程如图1所示。

图1 改进的Canny算法流程图Fig. 1 Improved Canny algorithm flow chart
首先输入图像,利用高斯滤波器降噪,使用改进的4方向模板进行一阶有限差分计算;接着进行非极大值抑制;然后使用结合截距法和人工蜂群算法的Otsu算法获取高阈值,并通过0.5倍高阈值获取低阈值;最后输出边缘检测结果图。
2.2 方向模板改进
为解决方向模板单一的问题,将2方向模板改进为4方向模板,充分利用倾斜方向的边缘信息解决导线弯曲部分边缘像素丢失的问题。4方向模板的角度包括 0°、45°、90°、135°,模板如图 2所示。
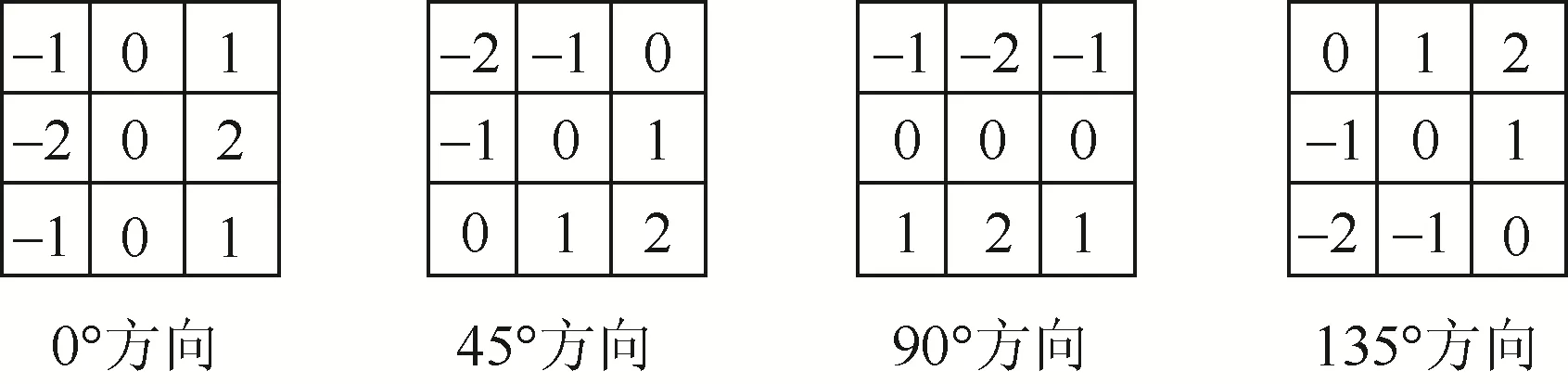
图2 4方向模板Fig. 2 4-direction template
经滤波处理后,对所得的导线图像使用以上4个模板进行线性处理,然后进行卷积运算,计算出各个像素点的梯度值和梯度方向。各个模板的计算方法如表2所示。

表2 各模板计算方法Tab. 2 Calculation method of each template
对得到的两组对角线方向的梯度值选择较大值,并将其转换到x轴和y轴上。x轴方向如式(4)所示,y轴方向如式(5)所示。
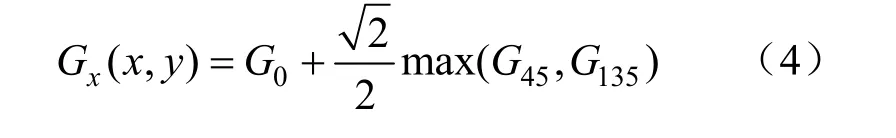
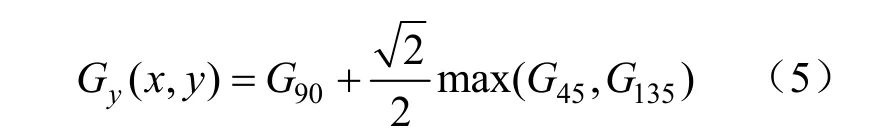
再利用公式(2)(3)分别求得每个像素点的梯度值以及梯度方向。
2.3 双阈值选取方法改进
本文通过结合截距法和人工蜂群算法改进传统二维Otsu算法[18]求出全局最佳高阈值θ2,并取0.5倍θ2为低阈值θ1。
(1)截距法
相较一维Otsu算法,二维Otsu算法利用了图像邻域中心灰度值与其邻域均值对构成的二维直方图进行分割,进一步提高了抗噪性[19]。但是,传统的二维Otsu算法引入了灰度值的信息内容,增加了运算量,严重降低了分割速度,从而降低了分割效率。
文献[20]提出用一维直线截距直方图代替二维灰度信息直方图,并通过求解直线最优截距作为图像最佳阈值的方法达到降维目的。
根据文献[20],直线i+j=k(i为像素灰度值,j为邻域灰度值,k为直线的截距)垂直穿过主对角线,则二维直方图中会有2L条与主对角线相垂直的直线,其范围是[0,2L–1]。每一条直线截距对应一个阈值,然后利用Otsu原理求解最佳阈值。
具体的改进过程如下:令直线截距表示图像分割的阈值T,大于阈值T的部分作为背景,小于阈值T的部分作为目标。令ω1表示目标区域的概率,令ω2表示背景区域的概率。结合一维Otsu的计算原理,则有:
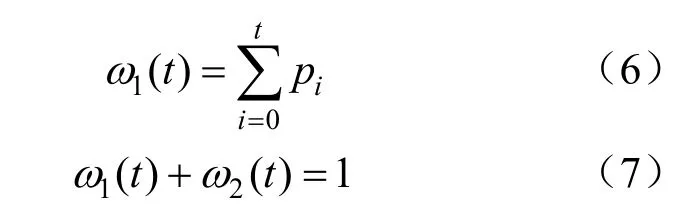
整个图像的总均值为:
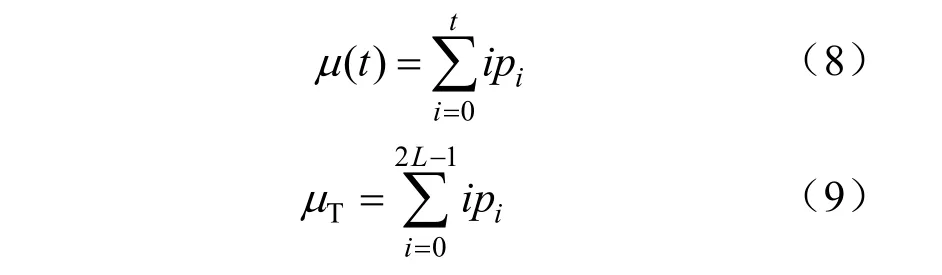
目标区域和背景区域的均值分别为:

将基于中心灰度值和邻域灰度均值的二维直方图转化为一维截距直方图,(L- 1 )×(L- 1 )的搜索空间压缩为2(L-1),从而大幅减少了计算量,有效地提高了分割效率;同时,弥补了传统二维Otsu算法因忽略图3中远离对角线部分的矩形噪声区域(A、D)对结果造成影响的缺陷。

图3 二维直方图投影Fig. 3 Two-dimensional histogram projection
(2)人工蜂群算法
用直线截距作为阈值的方法虽然保留中心灰度值与其邻域均值等信息,但是由于考虑了直方图的所有区域,部分区域的噪声值会被误判。结合截距法的Otsu直方图见图4。根据图4可知,直线在移动的过程中,远离主对角线部分的n1,n2中的噪声也会被分类到目标区域和背景区域中,因此可能无法获得最佳阈值,仍然需要提高算法的抗噪能力。
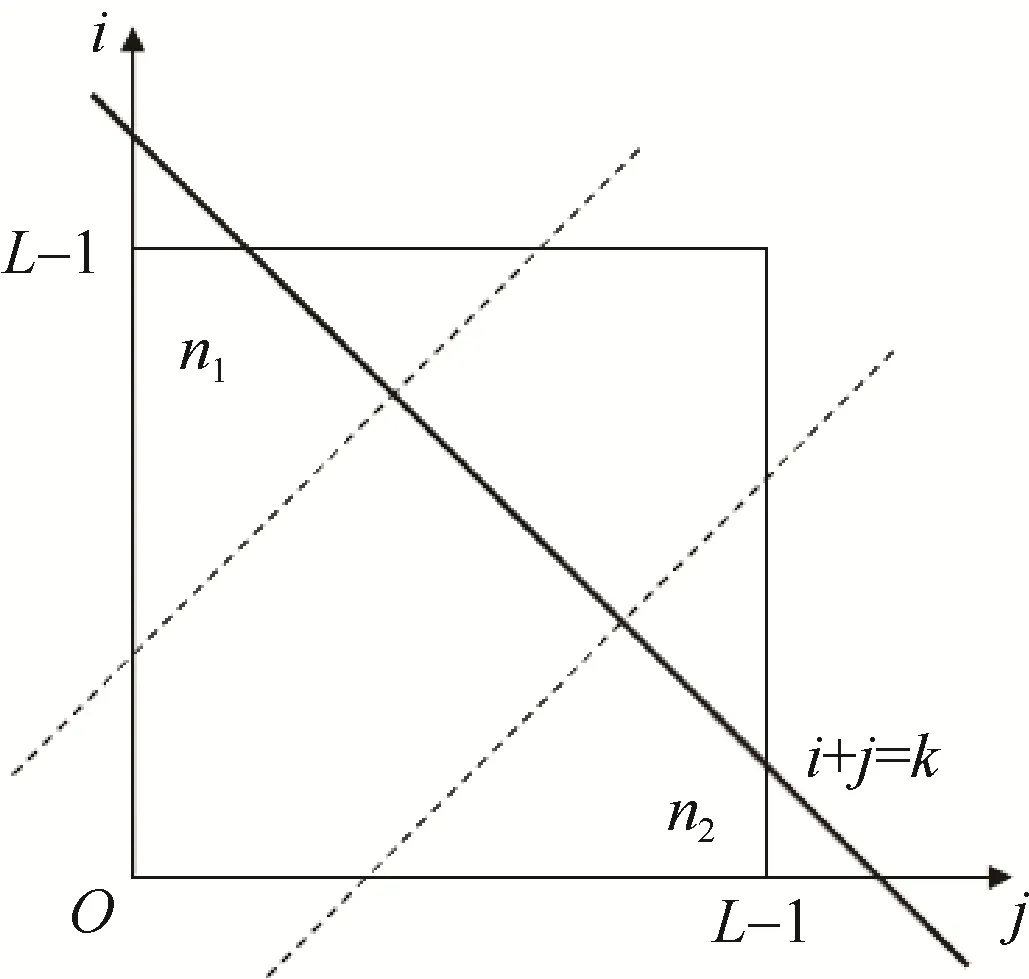
图4 结合截距法的Otsu直方图投影Fig. 4 Otsu histogram projection combined with intercept method
为了减少噪声对阈值选取的影响,本文引入人工蜂群算法[21](artificial bee colont optimization,ABCO)自动获取全局最优阈值。目标值函数为类间方差计算函数,见式(12)。人工蜂群算法的适应值函数fit为阈值选取函数,见式(13)。每个解的位置对应的目标值均代表一个阈值t。通过多次迭代获得解的最佳位置,即为目标值函数的最大值,从而获得最佳阈值t。
高教强国“中国模式”是立足中国高等教育实际的自主发展历程,有着区别于西方高等教育的独特发展逻辑,其主要特征是中国特色与全球视野的融合,体现出高教强国“中国模式”的中国和国际两个维度的时代价值。
寻找最佳阈值的流程如图5所示。

图5 人工蜂群算法流程图Fig. 5 Artificial bee colony algorithm flow chart
步骤1:根据式(14)随机初始化种群。

式中:xid代表第i个解(i=1,2,···,N),可用一个d维向量表示;ud和ld分别代表取值范围的上限和下限。
步骤2:雇佣蜂根据式(15)搜索可能的解,然后根据式(13)确定适应值,利用贪心策略选择较好解并向跟随蜂分享该解的信息。

式中:j=1,2,···,d;k=1,2,···,N,j≠k,且都为随机数;ε是[–1, 1]之间的随机数。
步骤3:跟随蜂根据式(16)计算跟随该解的概率。
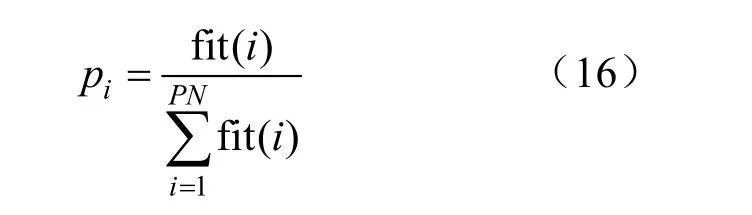
式中:fit(i)表示第i个食物源的适应值;PN代表食物源的个数。
步骤4:类似雇佣蜂的行为,跟随蜂根据公式(15)搜索可能的解,依次计算适应值并从中选择较好解。
步骤5:判断跟随蜂选取的解是否需要舍弃。如果因陷入局部最优时需要舍弃,则根据公式(17)生成侦查蜂随机寻找新解;否则记录当前的最优解。当达到最大迭代次数时输出最优解。

式中:xmin,j,xmax,j分别为第j维的最小值和最大值。
3 实验验证与分析
3.1 输电导线图像边缘检测结果
对照传统Canny算法和相关文献算法验证本文算法,其边缘检测效果如图6所示(图中加入了δ=0.03高斯噪声,图6(a)来源于文献[22])。由结果可以看出:传统Canny算子在进行导线的边缘检测时会丢失大量导线边缘信息且容易受到噪声影响。文献[23]算法在阈值选取时使用一维Otsu算法改进。该算法对导线进行边缘检测时获取到了导线的边缘信息,但是提取出的导线边缘部分区域存在不连贯现象,并且受到了噪声干扰,影响实验结果。利用文献[14]的Otsu-PSO改进算法选取阈值。该算法检测效果进一步提升,但出现单边有间断和小部分边界值丢失的情况,且局部依然受到噪声干扰的影响。本文的改进算法在以上算法的基础上加强了对细节的检测效果,使其能有效避免噪声对导线提取的影响,提高了导线边缘提取的完整度。

图6 导线边缘检测效果Fig. 6 Wire edge detection results
3.2 边缘检测图像评价指标
为准确评价本文提出算法的检测效果,使用图像边缘检测的3个评价指标进行量化比较。
(1)信噪比准则
均方根误差(eRMSE)与峰值信噪比[24](ePSNR)在图像检测领域中通常用于评判图像的噪声水平。eRMSE值越低,ePSNR值越高,图像的降噪效果越优秀。
各算法的eRMSE与ePSNR值见表3。结果表明,本文算法的eRMSE达到了最低值,ePSNR达到了最高值,在抗噪性上抗噪性上均优于其他算法。
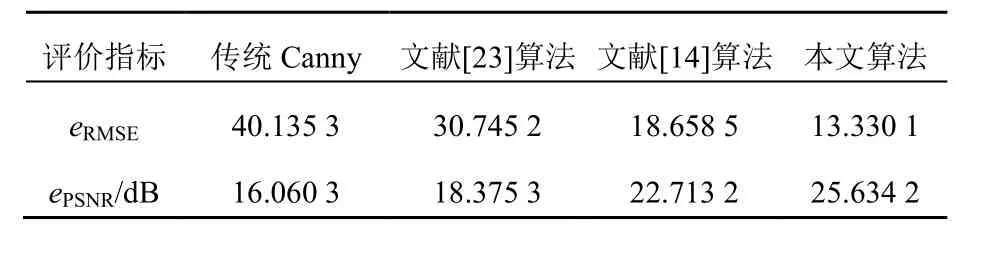
表3 信噪比评价指标Tab. 3 Signal-to-noise ratio evaluation index
(2)定位精度准则
结构相似性[25](eSSIM)用于评估图像质量状况,可以定量分析检测后的图像与原图像的相似程度,其由亮度、对比度和结构3种对比方式组成。eSSIM值越高,图像的检测精度越精准,各特征与原图越接近。
计算结果见表4。由结果可以看出,本文算法准确度比其它几种算法均有所提升。

表4 定位精度评价指标Tab. 4 Positioning accuracy evaluation index
(3)单一边缘响应准则
对每幅图像分别统计边缘检测像素总数A,4连通域数B,8连通域数C;并计算C与A和B的比值关系,结果见表 5。当C/A值越小时,提取出的图像边缘特征越连贯;当C/B值越小时,单像素边缘所占比例越大,越符合单一边缘响应准则[22]。由表5的数据可以看出,本文算法的C/A值与C/B值均低于其他算法。

表5 边缘检测数统计Tab. 5 Edge detection count statistics
(4)实验数据结果
对8张输电导线图片分别使用传统Canny算法、文献[14,23]算法和本文算法进行检测,相关评价指标的检测结果如图7所示。
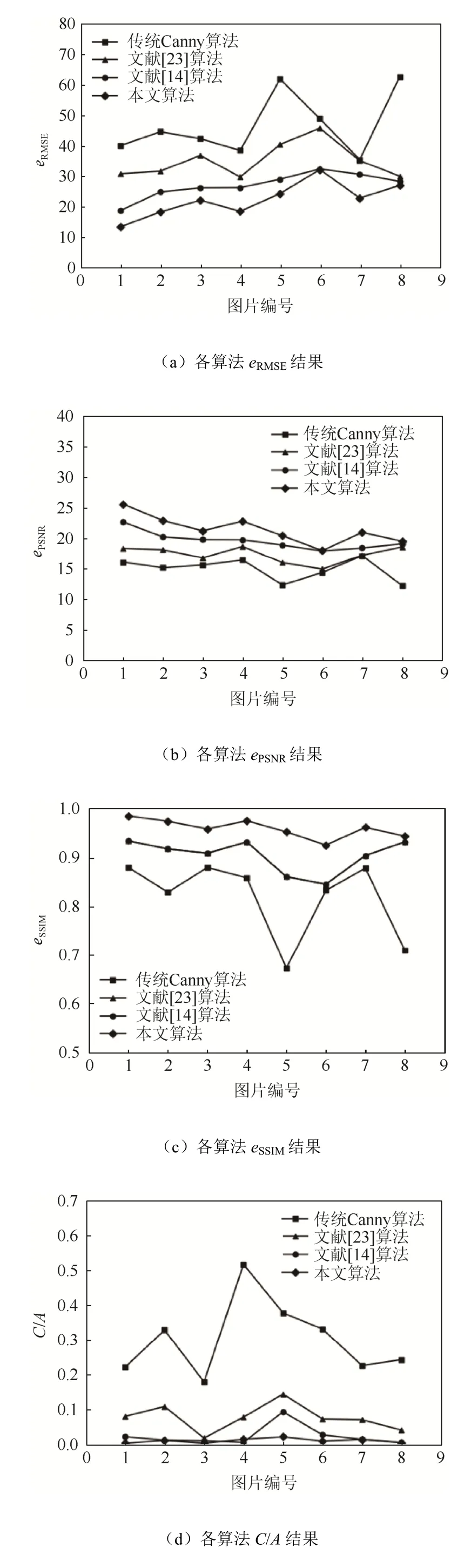
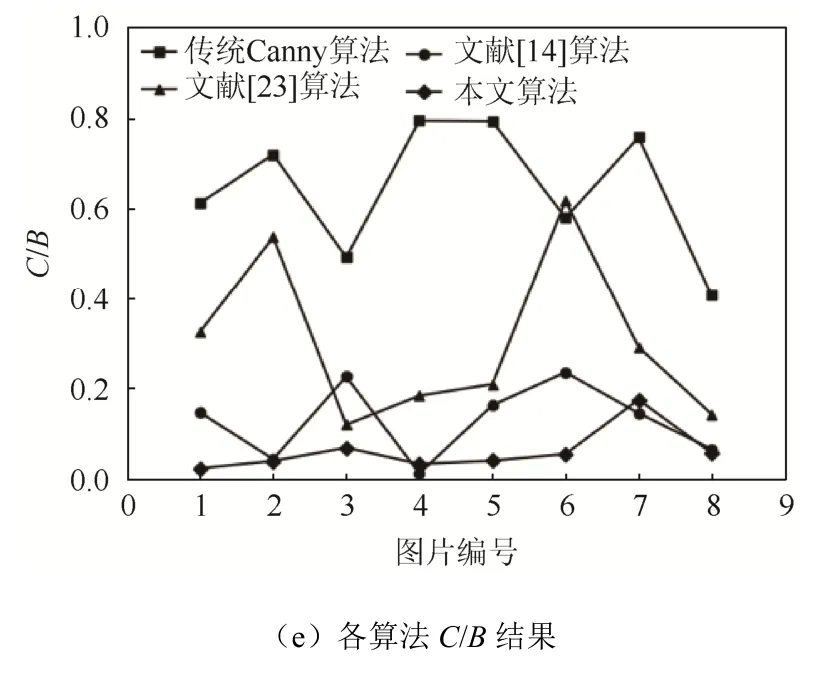
图7 边缘检测评价指标的检测结果Fig. 7 Edge detection evaluation index detection results
由图7可以看出,文献[14]算法的ePSNR平均值和eSSIM平均值分别为19.613 9和0.943 3,本文算法的ePSNR平均值和eSSIM平均值分别为21.454 2和0.959 4。与文献[14]算法相比,本文算法的ePSNR平均提高了9.38%,eSSIM平均提高了1.7%,单一边缘指标均有较大提升。
4 结论
结合输电导线图像处理,本文针对传统Canny算子存在模板选取和阈值选取的问题,对算法进行了改进,增强了方向模板多样性和阈值选取自适应性。经实验验证,本文改进算法在检测效果上具有能够连贯识别导线边缘信息、增加边缘细节的特点,同时抑制了噪声干扰和虚假边缘;在阈值选取过程中引入了人工蜂群算法选取阈值后,算法在寻找全局最优值方面更具优势,有利于导线图像的后续研究工作。

