基于改进广义预测控制的过热蒸汽温度优化
杨 硕,张 悦
(华北电力大学 控制与计算机工程学院,河北 保定 071003)
0 引言
随着“碳达峰、碳中和”能源战略目标的提出,超(超)临界机组已逐步成为我国的主力发电机组。随着新能源并网需求日益增加,火力发电的建设目标已逐步从信息化、自动化向智能化转变;大数据电厂、智慧电厂成为新的发展方向。过热蒸汽温度作为机组安全与经济运行的重要参数之一,其控制常采用串级控制策略来实现[1]。然而,超(超)临界机组的过热汽温对象具有非线性、大滞后的特性,使其成为控制难点[2]。因此,需要进一步提升大型火电机组过热汽温的控制品质。
近年来,许多学者利用先进控制算法或改进算法来提升过热汽温的控制性能。文献[3]利用线性自抗扰控制器代替 PID,设计了汽温的串级优化控制方案;在不同工况下采用果蝇算法优化相应的控制器参数。文献[4]在对汽温控制系统模型辨识的基础上,设计了基于逆向传递的网络化预测控制方案,并应用于直流锅炉过热汽温控制系统中,以更好地适应对象特性的变化。文献[5,6]将广义预测控制应用在过热汽温控制系统中,利用GPC中滚动优化环节求解目标最值,以达到优化目的。在常规广义预测控制的基础上,文献[7]改进了GPC算法中的控制性能优化参数,针对机组变工况,通过PI反馈结构增强了过热汽温控制系统的鲁棒性,使系统有更好的控制品质。此外,文献[8]提出自抗扰控制–线性自抗扰控制(ADRCLADRC)串级控制策略,并针对其中控制器参数利用多目标粒子群算法进行整定优化。文献[9]借助改进的自抗扰控制(ADRC),以解决高阶动态对扰动滞后响应的影响,进一步改善了过热蒸汽温度的控制性能。在此基础上,文献[10]提出了一种基于混合自抗扰控制的单环控制策略,并解决了ADRC中多个参数整定的方法,进一步改善了过热汽温系统的控制性能。针对深调峰超超临界机组,文献[11]借助模糊切换,提出了仿人智能控制算法,并基于此设计了再热汽温优化控制系统;针对其中的参数,采用经验优化后的粒子群算法进行整定选择;仿真结果表明该设计系统能够有效提高再热蒸汽温度系统的鲁棒性。
上述文献中,大部分的控制方法仅考虑了机组单一负荷下的控制效果,且控制性能未能从多角度考量。本文基于阶梯式广义预测控制算法,针对超超临界机组设计了过热蒸汽温度控制系统。首先采用模拟退火算法改进粒子群算法,并将其应用于GPC的滚动优化环节中。针对某600 MW机组直流锅炉进行仿真实验,在满足不同负荷要求的前提下,从给定值跟随、抗干扰性和负荷适应性3方面进行对比研究,以验证所提出控制方案的效果。
1 直流炉过热汽温控制系统
在超临界机组过热汽温控制系统中,如果汽温控制产生较大的波动,会直接影响汽轮机的安全运行,因此一般将汽温波动控制在±5 ℃的范围之内[12]。系统结构组成如图1所示。

图1 过热蒸汽温度串级控制系统结构Fig. 1 Superheated steam temperature cascade control system structure
以减温器为中点,按照过热蒸汽的流通顺序,将减温器前称为汽温导前区,减温器后称为惰性区。当喷水减温器出口温度θ1发生变化时,内回路中副调节器输出会使减温水量 W 发生改变,从而控制惰性区过热器出口的蒸汽温度 θ2基本不变。
在过热汽温控制系统中存在多种干扰因素,包括锅炉负荷变化、减温水量以及减温水温度的变化等。这些干扰增加了控制难度。副回路主要用于抑制这类不可测扰动,其在实际应用中常采用P或者PI控制器;而在主回路则常采用PID控制。
2 改进的GPC算法
2.1 GPC算法
GPC被应用于各类控制系统中,由预测模型、滚动优化、在线反馈校正等基本要素[13]构成,其结构如图 2所示。图中,w(t)为给定值,u(t)和 y(t)分别为控制系统输入和输出,yˆ( t)为预测输出。
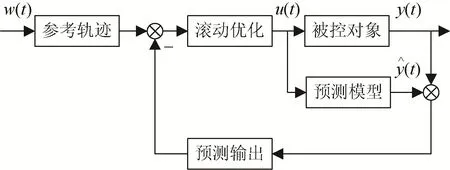
图2 预测控制基本结构Fig. 2 Basic structure of predictive control
(1)预测模型
将火电机组锅炉的过热蒸汽温度控制系统CARIMA模型表示为[14]:

式中:A(z–1)、B(z–1)、C(z–1)分别为 na、nb、nc阶的z–1多项式,具体形式如公式(2)所示;ξ(t)属于白噪声序列;Δ为差分子算子,且Δ=1–q–1。

(2)滚动优化
设定GPC采用如下的优化目标函数:

式中:w(t+j)、y(t+j)分别为为优化对象的参考值和输出;λ为控制权重系数,且λ>0;n和m分别为算法的预测和控制长度,且m≤n。
(3)输出预测
为了得到(t+j)时刻的系统优化预测输出值及y(t+j),在GPC算法中引入丢番图方程[14]:

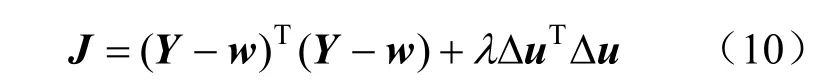
滚动优化中求解最优控制率,针对Δu进行求导并使结果为0,则Δu为:

在实际中,将控制系统加入(GTG+λI)的第一行中,即:
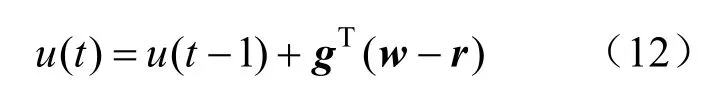
由以上分析可知,传统GPC需要对矩阵进行逆运算,其中包含较大的计算量,使得其在实际的控制系统中难以做出快速响应[15]。
基于此,本文选用阶梯式广义预测控制算法(SGPC),其主要思想是:以阶梯式控制来约束 GPC中的未来控制量,简化整体运算过程,充分发挥GPC算法具有的良好抗干扰性和稳定性[16]。
同样针对模型(1),在 GPC的基础上引入式(13)。阶梯式广义预测控制中,将 Δu比例化,如下:


通过以上的变化,使得n×n的矩阵G转化为列向量 G*,从而可以大大降低计算量,简化了运算。
至此,本文在传统广义预测控制算法的基础上进行改进,解决了其中计算量大的问题,得到了阶梯式广义预测控制算法。
2.2 基于改进粒子群算法的SGPC
粒子群优化算法(PSO)的全局搜索能力与其种群多样性有密切联系;如果其种群多样性无法保证,就会产生陷入局部最优的问题,严重影响算法性能[17]。针对这一问题,借助模拟退火算法对粒子群算法进行改进,形成融合算法,即SA-PSO算法。核心思想是模拟退火机理:在温度慢慢下降的过程中,如果固体的开始温度达到一定高度,且持续时间足够长,就可以避免出现局部最优问题,得到全局的最优解[17]。因此可将该退火机制引入到传统的粒子群算法中。文献[17]和[18]都对 SA-PSO融合算法进行了详细的阐述,本文不再赘述。
为了弥补SGPC算法实际应用中在受约束控制问题上的缺点,需增强GPC在约束空间内的搜索能力。将改进后的PSO算法应用在广义预测控制的滚动优化环节。
针对公式(3)重新描述为最优目标函数,即:

针对GPC面临控制增量的约束问题,SA-PSO算法将约束看作待优化变量的搜索范围,并引入到优化环节中,则其改进后的SGPC算法流程如图3所示。

图3 改进的SGPC算法流程图Fig. 3 Improved SGPC algorithm flow chart
为了验证改进方法的有效性,设被控对象如式(20)所示:
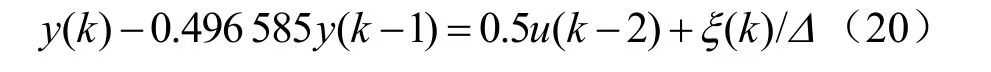
式中:y(k)为采样当前实际输出;ξ(k)是[–0.2, 0.2]均匀分布的白噪声。
采用改进后的阶梯式广义预测控制算法,其中对应参数设置为:预测步长 N=6,控制步长M=5,加权系数 λ=1,遗忘因子 μ=1,柔化系数α=0.5,阶梯因子 β=0.3。在相同参数条件下与常规的广义预测控制进行控制效果仿真对比,结果如图4、图5所示,包括输出yr(k)、y(k)以及最小方差控制律u(k)。
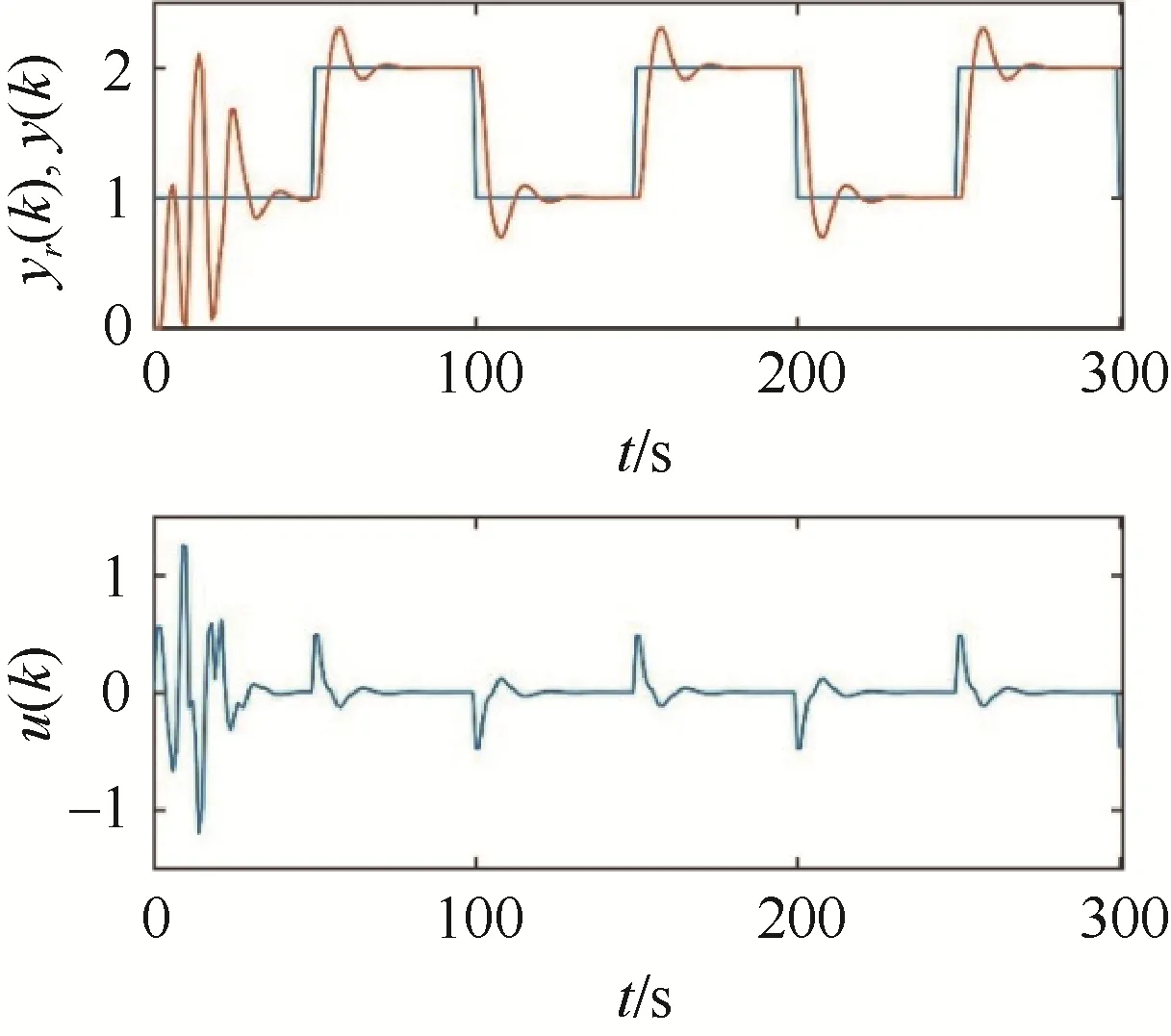
图4 传统GPC仿真结果Fig. 4 Simulation results of traditional GPC
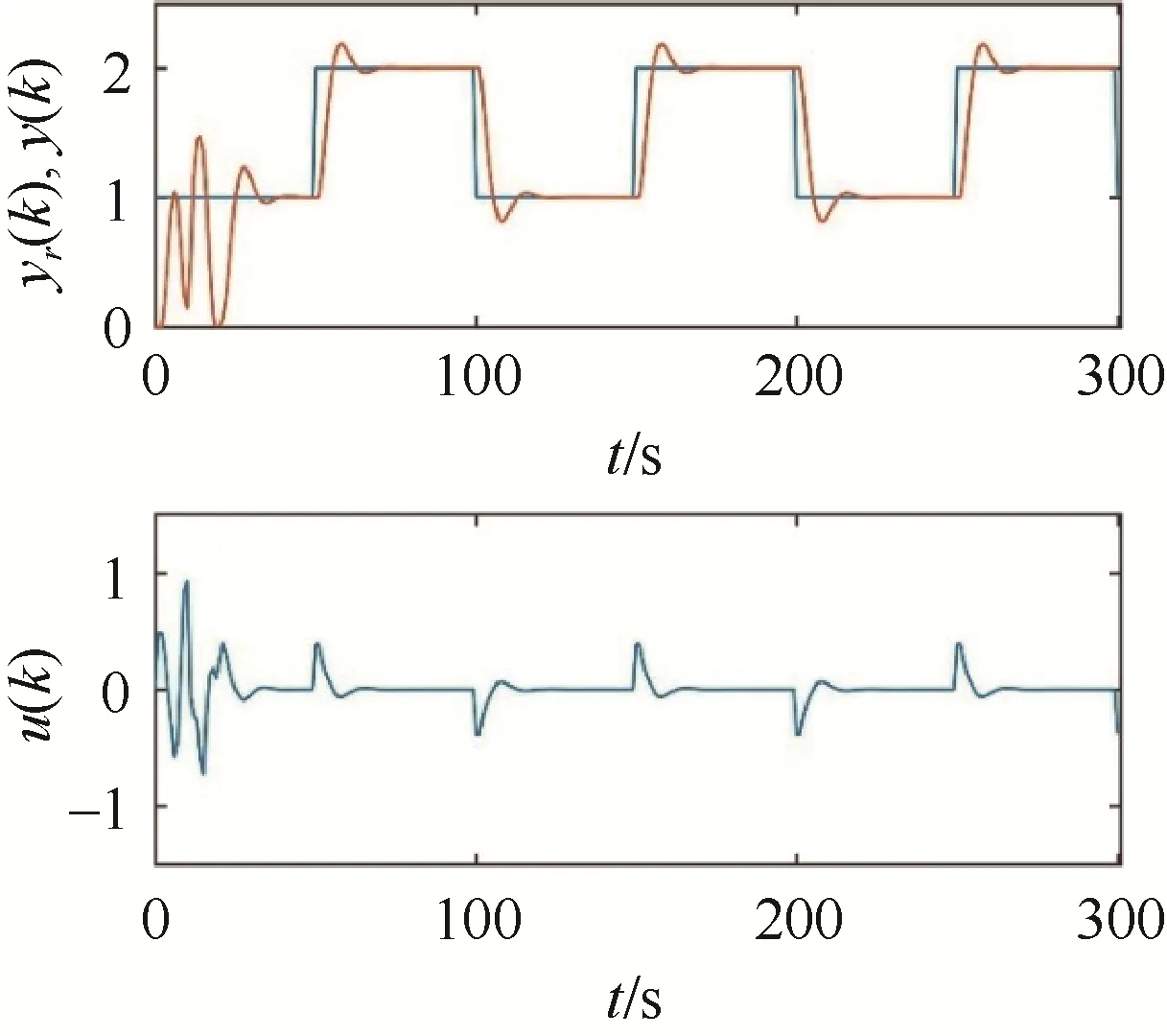
图5 改进GPC仿真结果Fig. 5 Simulation results improve GPC
从图4和图5对比分析可得,改进后的阶梯式广义预测控制算法对系统跟踪效果好,计算量小且能够快速跟踪设定值,整体性能优于常规的广义预测控制。
对比最小方差控制率u(k)的变化曲线:在图4中,对于传统GPC,前50 s内的变化范围是[–1.20,1.25],经过调节后达到稳定输出时的变化范围是[–0.48,0.49];而在图5中,改进后的GPC前50s内的变化范围是[–0.72,0.93],经过调节后达到稳定输出时的变化范围是[–0.39,0.39]。可见,经过SA-PSO算法优化后,控制量变化趋势更加平缓。
本报讯为进一步提高企业班组长管理水平和工作水平,大力推进基层班组长队伍建设,全面提升班组长队伍整体素质,促进班组建设工作不断发展,立足岗位创新创造,10月16日上午,泸天化股份公司举行了班组长管理创新经验分享活动。
3 过热汽温优化控制系统设计
针对过热蒸汽温度这一被控对象,选取文献[19]中超临界机组600 MW直流锅炉的参数进行仿真实验。文献[20-22]已经论证了该模型具有良好的拟合性。典型工况下导前区 G1(s)和惰性区 G2(s)的传递函数如表1所示。
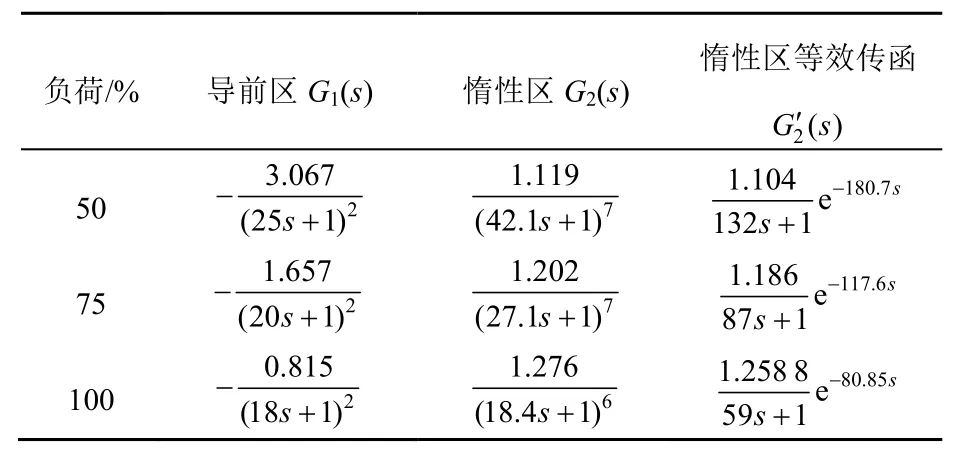
表1 典型工况下过热汽温的传递函数Tab. 1 Transfer function of superheated steam temperature under typical working conditions
由表1可知,被控对象过热汽温具有大惯性的特点,且在不同工况下的惯性时间和传函静态增益相差较大;因此在变负荷过程中,其对控制系统有较高的要求。考虑到过热汽温的这些特性,常规的PID串级控制方案难以满足当前电力发展的控制要求[23],因此引入广义预测控制(GPC)。为了避免算法中的矩阵可逆性运算,选取阶梯式广义预测控制(SGPC),并将改进的粒子群算法应用于滚动优化环节[24],最终设计了超临界机组过热汽温控制系统,其优化控制方案如图6所示,其中r、y为过热汽温的设定值和输出值,d为减温水扰动。

图6 基于改进GPC的过热汽温控制系统Fig. 6 Superheated steam temperature control system based on improved GPC
在该过热汽温串级控制系统中,主调节器采用了改进的阶梯式广义预测控制,以 SA-PSO算法优化其中的控制量;而副调节器仍采用传统的控制手段,即比例积分调节(PI),控制器参数为 Kp1,Ti1。
4 仿真验证
为了验证提出的基于改进 GPC过热蒸汽温度控制系统的有效性,借助MATLAB仿真,将改进的阶梯式GPC与传统GPC以及PID做控制效果对比。
在仿真实验中,考虑了3种不同工况:首先利用模型参数做给定值跟随实验,以对比改进前后GPC控制以及普通PID控制的控制效果。在这基础上,加入减温水扰动,来对比上述3种控制的抗干扰能力。最后采用其中一组工况下的模型参数,变换工况,更改控制对象模型做给定值跟随实验,以观察改进后的阶梯式GPC是否具有变工况适应性。
对于不同负荷下各个串级控制系统参数设置,改进后的 GPC 参数包括 N=6,M=5,λ=1,μ=1,α=0.5,β=0.2;而 PI和 PID 控制器参数(Kp1,Ti1,Kp2,Ti2,Td2)整定采用Z-N整定法[25-26],如表2所示。

表2 不同工况下PI和PID控制参数表Tab. 2 PI and PID control parameter table under different working conditions
4.1 不同工况
针对锅炉在不同工况下的模型,采用传统PID、改进的SGPC进行仿真。各控制方法下,单位阶跃响应曲线对比如图7所示。
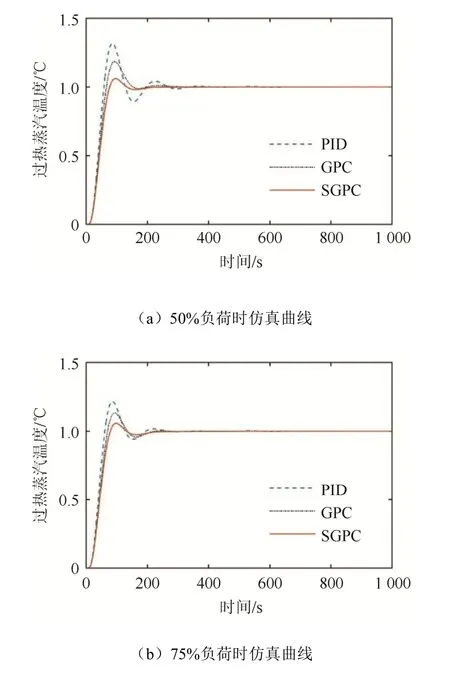

图7 不同负荷控制系统响应曲线Fig. 7 Response curves of different load control systems
测得各曲线中对应3种不同控制方法下的调节时间ts和超调量σ,数据如表3所示。

表3 不同工况3种控制策略性能指标Tab. 3 Performance indicators of three control strategies under different working conditions
由图7和表3可知,常规PID控制超调量较大,且调节时间较长;而SGPC的控制效果明显优于传统的GPC和PID:对应不同负荷下的过热汽温控制系统具有更加良好的动态响应特性,且超调量小。在 100%负荷下,其超调量为 2.3%,调节时间短,表现出更好的控制效果。
4.2 给定值跟随性
选取 100%负荷下的模型进行过热汽温设定值改变仿真实验。当控制系统稳定之后,设定值在500 s时从1增至1.2,到1 000 s时再降至1。单位阶跃响应结果如图8所示。

图8 100%负荷下给定值跟随仿真Fig. 8 Set value following simulation under 100% load
从图8中可以看出,改进后的SGPC比传统GPC以及PID有着更好的平稳性,超调量明显较小,体现出较好的设定值跟随性。
4.3 抗干扰性
系统稳定后,在500 s时,加入减温水扰动,不同工况单位阶跃响应曲线仿真结果见图9。
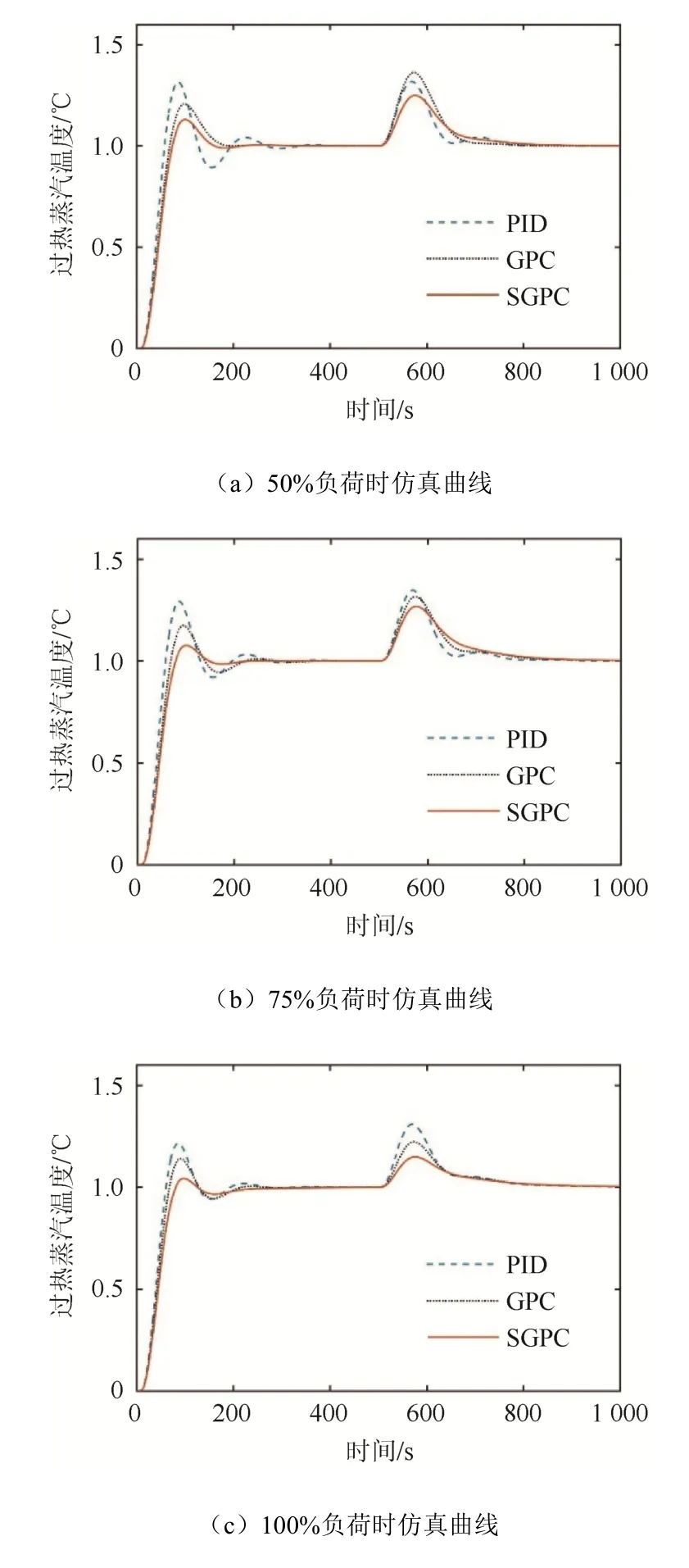
图9 加入扰动后的响应曲线Fig. 9 Response curve after adding disturbance
分析图 9可知,在不同负荷下,改进后的SGPC表现出更好的抗干扰性能,能快速抑制减温水扰动。在 50%负荷下,传统的GPC抗干扰性不及PID控制效果,而改进的方案有效改善了这一不足。
4.4 负荷适应性
仿真实验中,系统开始以100%负荷运行,在1 000 s时负荷降为50%。单位阶跃仿真曲线如图10所示。

图10 变负荷时系统输出响应曲线Fig. 10 System output response curve under variable load
由图 10可知,过热汽温控制系统在负荷从100%降到50%后,传统PID控制由于控制器参数未改变,会出现较大的波动。相比之下,改进后的SGPC能够很大程度上抑制变负荷过程中产生的扰动,使系统快速达到稳定状态。
5 结论
本文采用模拟退火算法改进了粒子群算法,避免其出现陷入局部最优问题;再将该 SA-PSO融合算法引入广义预测控制的滚动环节中,弥补了其中受约束控制问题的缺点;选用阶梯式GPC,进一步简化算法计算。仿真实验表明:相比传统的GPC,改进后的SGPC控制效果更好,证明了该方法的有效性。
针对超临界600 MW机组,设计了基于改进后的阶梯式GPC过热蒸汽温度控制系统。仿真结果表明,在3种典型工况下,相比传统GPC和PID,改进后的SGPC在给定值跟随性、抗干扰性2方面都有更好的控制性能,且在变负荷时具有良好的稳定性能,能快速使控制系统恢复稳定状态;故提出的控制策略整体上优化了过热蒸汽温度系统的控制性能。

