冲击回波声频法在桥梁孔道压浆密实度检测中的应用研究

邢厚俊 葛宁 贾其松 邓立 马永强 吴佳晔，4 冯源

1.中国国家铁路集团有限公司工程质量监督管理局，北京100844；2.哈尔滨铁道职业技术学院，哈尔滨150060；3.四川升拓检测技术股份有限公司，四川自贡643000；4.西南石油大学，成都610500

冲击回波声频（Impact Acoustic Echo，IAE）法是一种用拾音器代替拾振传感器拾取被测物体的振动信号，并进行频谱分析的检测方法。IAE法在铁路隧道衬砌检测［1-2］、CRTSⅢ型板式无砟轨道脱空检测中得到了较好的应用。

为了研究IAE法在桥梁预应力孔道压浆密实度检测中的适用性和测试精度，本文首先对现行预应力孔道压浆密实度无损检测方法的优缺点进行分析，比较IAE法与冲击回波（Impact Echo，IE）法的异同，然后通过模型试验和现场试验对比IAE法与IE法的测试效率和精度。

1 现行孔道压浆密实度检测方法概述

1.1 现行无损检测方法的优缺点

按检测所采用的媒介来划分，预应力孔道压浆密实度无损检测方法可分为基于电磁波的检测方法（地质雷达法）、基于放射线（X光、伽马射线）的检测方法、基于超声波的检测方法（阵列式超声波脉冲回波法）和基于弹性波的检测方法（IE法）［3-8］。各方法采用的物理媒介不同，其检测效果也存在差异。

由于受金属屏蔽，地质雷达法不适合用于铁皮波纹管和钢筋密集区，尤其是钢筋密集、压浆又容易出现缺陷的梁端部位。基于放射线的检测方法尽管检测精度高、直观性强，但由于具有放射性、检测成本高，在国内应用很少。阵列式超声波脉冲回波法（Ultrasonic Pulse-Echo，UP-E）理论上也可以检测压浆缺陷，但同样受钢筋干扰大，实际应用很少。IE法以冲击弹性波为媒介，因其测试方便、适用范围广、精度较高，在桥梁预应力孔道压浆密实度检测中逐渐成为主要方法。

1.2 IE法存在的问题

IE法需在静止条件且传感器与被测物体表面接触后才能检测，从而大大降低了测试效率，且无法连续测试。传感器的固定方法（压着式、紧固式、黏结式）和固定状态对测试结果影响大。采集信号的加速度传感器需要耦合在被测物体的表面。由于传感系统本身的共振特性，接触状态不良或传感器固定方式的差异都有可能引起测试误差，从而导致误判。为提高测试效率，实际检测中常采用压着式固定，但用力过大或者传感器与测试物体表面接触不良时，传感系统的共振频率会降低，测试结果会受到严重影响。

为了解决上述问题，学者们做了大量改进工作，但IE法的固有问题未得到根本解决，对较厚梁体的孔道压浆密实度测试难度依然较大。JGJ/T 411—2017《冲击回波法检测混凝土缺陷技术规程》中指出冲击回波法适用于检测厚度为20～60 cm的薄板，然而铁路桥梁大部分预应力混凝土梁的梁板厚度超过60 cm。

2 IAE法

2.1 IAE法信号采集原理

IAE法的优点在于非接触式拾取被测物体表面的振动信号，进而避免由于接触带来的一系列问题。非接触式拾振设备中，最具代表性的激光多普勒测振仪成本高且体积庞大，在实际工程检测中难以普及，因此以拾音器为传感器的IAE法日益受到关注。

拾音器采集的是空气振动信号。对被测物体激振后，物体表面的振动会压缩（拉伸）附近空气并诱发空气振动，产生声音信号。它能反映测试点混凝土的振动特性［1］，通过广频域、高指向拾音器拾取。

2.2 IAE法与IE法的对比

IE法所用的加速度传感器与IAE法拾音器所采集的信号及采集方式有一定的差异。具体体现在：

1）物理量不同

被测物体振动体现在质点的位移、速度和加速度。而拾音器无论是动圈式还是电容式，得到的物理量均为空气压强差。以一维x方向为例，气体的运动方程为

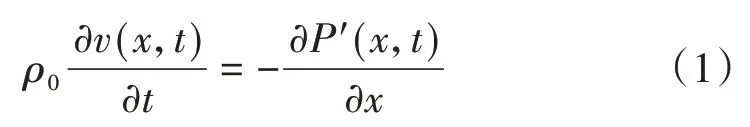
式中：ρ0为空气初始静止时的密度；t为空气振动过程中某一时刻；P′(x，t)、v(x，t)分别为空气压强差和空气流速。

由式（1）可见，空气压强差对位移的微分与其速度对时间的微分（即加速度）呈线性关系。因此，可差分处理计算空气柱的加速度。当拾音器与被测物体足够近时，考虑到空气质点与物体表面同步运动，可近似地认为空气的加速度与物体表面的加速度一致。

2）测试区域不同

采用加速度传感器、激光测振仪测试的只是被测物体上某一点，其他部位的振动状况并不会反映在测试信号中。由于空气具有流动性，拾音器采集的信号范围要大得多。为了使其适用于IE法检测，需要对拾音器进行隔音设计。

3）传感器频率范围不同

加速度传感器的共振频率会随传感器与被测物体的耦合状况发生变化，进而带来测试误差。拾音器则不存在明显的共振频率，信号采集的稳定性更好，受被测物体表面状态的影响小。这也使得IAE法测试效率较IE法有所提高。

值得注意的是，空气层对原始振动信号中的微弱成分有削弱作用，因此IAE法信号灵敏度会低于IE法。这就要求在分析方法的选择上应更加注意。

3 模型试验和现场验证

为验证IAE法在预应力孔道压浆密实度检测中的可行性，分别进行了模型试验和现场试验。

3.1 模型试验

混凝土模型梁厚度从20 cm渐变到40 cm，孔道居中，塑料波纹管直径10 cm，灌浆密实无缺陷。分别采用IE法与IAE法进行检测。测试数据的频谱等值线见图1。可见：IE法梁底反射信号离散，而IAE法梁底反射信号集中且连续，信号变化趋势同梁实际厚度相符。

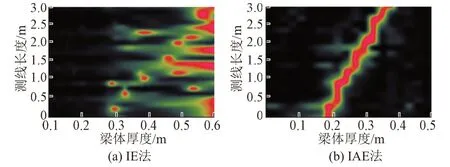
图1 模型梁频谱等值线

3.2 现场验证

3.2.1 厚度渐变T梁

对一梁场厚度渐变T梁进行检测，距梁端0～0.8 m厚度70 cm，距梁端0.8～4.0 m厚度从70 cm渐变到35 cm。分别采用IAE法和IE法沿同一测线进行检测，结果见图2。可见：IE法频谱等值线在梁厚度超过0.5 m时变得杂乱，难以进行准确判断，而IAE法频谱等值线在梁体渐变段信号非常清晰、连续，并在测线0～0.7 m存在频谱信号提前、滞后现象，此为典型缺陷信号特征。经开孔验证，该处孔道压浆不密实。

图2 厚度渐变T梁频谱等值线

3.2.2 厚75 cm现浇梁

采用IAE法对一桥梁中厚75 cm现浇梁W03Y—W06Y四个孔道压浆密实度进行了检测。孔道W03Y、W06Y检测结果见图3。可见：存在反射信号明显滞后现象，将其判定为压浆缺陷。经开孔验证该处有空洞。

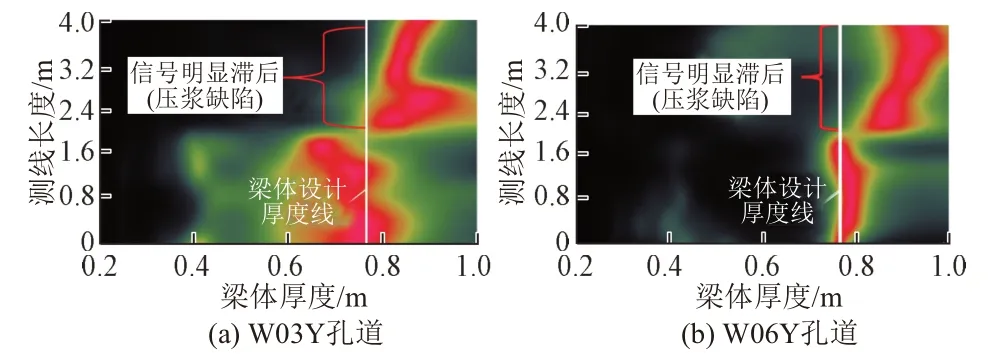
图3 厚75 cm现浇梁孔道IAE频谱等值线

3.2.3 厚度小于0.25 m箱梁

采用IAE法分别对预制梁场厚度小于0.25 m的箱梁上压浆密实孔道进行检测，结果见图4。可见，频谱信号出现明显双频现象，无法对梁体厚度及压浆密实情况进行分析。原因主要为IAE法信号与IE法信号均由激振锤敲击产生，梁板较薄时敲击易引起梁体弯曲振动，该振动信号也会被拾音器所采集，从而对有效信号造成干扰。为解决这一问题，引入经验模态分解（Empirical Mode Decomposition，EMD）法［9］进行滤波分析。

图4 厚度小于25 cm箱梁孔道IAE频谱等值线

4 基于EMD的滤波算法

EMD法将采集的数据分解为各阶分量数据，即本征模态函数（Intrinsic Mode Function，IMF）分量。为了将IAE法采集的数据中存在的梁板弯曲振动信号滤除，采用基于EMD的滤波算法进行处理。步骤如下：①对IAE数据进行EMD分解，提取各阶IMF分量；②对IAE数据和各阶IMF分量的相关性进行分析；③删除相关系数小于0.2的IMF分量后重构信号；④对重构的IAE数据进行频谱分析。

采用EMD法对3.2.3节所采集的数据进行分解，计算IAE数据与各阶IMF分量的相关性r，结果如图5所示。

图5 EMD分解图

删除相关系数小于0.2的IMF1—IMF3阶数据，进行数据重构，对重构后的数据进行频谱分析得到频谱等值线，见图6。薄板数据经过滤波处理后反射信号位置与梁体设计厚度线相符，双频现象消失，可判断该孔道压浆无缺陷，证实基于EMD的滤波算法可有效滤除IAE数据中存在的薄板弯曲振动信号。

图6 厚度小于25 cm箱梁IAE数据经EMD滤波后频谱等值线

5 结语

经理论分析及试验验证，IAE法能对桥梁孔道压浆密实度进行有效测试。基于EMD法的滤波算法能有效滤除IAE法测试薄板结构（厚度小于25 cm）时产生的弯曲振动信号。IAE法在测试效率、测试稳定性、适用范围（厚度）等方面均比IE法显著提高，为铁路预应力混凝土桥梁孔道压浆密实度检测提供了新的无损检测方法。

IAE法尽管提出时间不长，但已在隧道衬砌的厚度和缺陷、无砟轨道脱空、预应力孔道压浆密实度检测等方面体现出了优越性。经过不断试验、改进和应用，IAE法会进一步得到完善和发展。