层状围岩流变荷载作用下隧道二次衬砌裂损特征

余龙文

中铁二十三局集团第三工程有限公司，成都 611137

层状岩体是隧道施工中常见的岩体，由于软弱面的存在，其物理力学性能具有显著的各向异性特征［1］，导致隧道开挖后围岩的破坏机制与支护体系的力学行为均体现出较强的方向性［2］。周晓军等［3］基于室内相似模型试验，揭示了层状岩体二次衬砌受力的偏压效应及结构的破坏模式。夏同彬［4］采用室内三维模型试验，对层状岩体中锚杆的支护力学机理及支护的优化措施进行了分析。沙鹏等［5］结合兰渝铁路两水隧道，通过现场实测分析了软弱层状岩体隧道支护体系的受力特性。张志强等［6］基于FLAC 3D软件研究了层状岩体地层中锚杆的剪切断裂与拉伸断裂行为。秦二涛［7］基于数值模拟与现场试验，提出了控制深埋薄层状岩体大变形的锚杆非对称支护措施。

层理面的存在显著影响结构的长期力学行为。Giovanni等［8］以里昂—都林基线隧道的辅助坑道为例，研究了非对称流变挤压大变形下让压型钢拱架支护的力学性能。Chen等［9］以成兰铁路茂县隧道为例，研究了层状千枚岩地层支护体系的长期力学行为，提出采用双层钢支撑来抑制围岩的非对称流变变形。王更峰［10］以兰渝铁路多座层状碳质板岩隧道为背景，研究了流变荷载作用下支护结构受力时空效应的演化规律。

随着隧道运营年限增加，软弱层状围岩的流变效应更加显著，导致二次衬砌出现开裂［11-12］，影响隧道结构的长期安全运营。目前，关于层状岩体流变效应作用下二次衬砌的裂损问题研究较少。因此，本文建立基于颗粒离散元理论的层状岩体各向异性流变模型，结合离散元-有限差分耦合平台，对层状岩体流变效应作用下二次衬砌的开裂过程进行研究，并揭示地应力场及衬砌背后空洞对衬砌破坏特征的影响规律。

1 数值模拟方法

1.1 连续-离散耦合方法原理

为了兼顾衬砌结构裂纹的精细化模拟及数值模型的计算效率，建立颗粒流程序（Particle Flow Code，PFC）颗粒离散元及FLAC有限差分耦合模型进行计算。由于FLAC网格单元的节点力不能直接通过PFC颗粒单元得到，在颗粒单元与FLAC网格单元之间建立耦合单元（墙体）作为传力媒介，详细的耦合过程可参考文献［13］。

1.2 基于颗粒离散元的各向异性流变模型

1.2.1 数值模型

PFC中的黏结颗粒模型（Bonded Particle Model，BPM）［14］采用平行黏结（Parallel Bond）和接触黏结（Contact Bond）来表征颗粒间的黏结特征。层状岩体离散元数值模型中结构面与岩石基质体均采用BPM模型进行描述。为表征岩石流变各向异性，改变颗粒间的接触类型，即将线性接触改变为Burgers接触，以实现岩石的流变效应。

层状岩体流变数值模型的建模过程及参数标定过程如下（以压缩试样为例）。

1）生成尺寸为50 mm（宽）×100 mm（高）的各向同性压缩试样。颗粒半径最大值与最小值之比取1.6，颗粒半径最小值取0.28 mm，颗粒尺寸满足高斯分布，平行黏接半径因子取1。

2）在各向同性试样中生成一组平行分布且间距为7 cm的软弱结构面。

3）根据室内压缩试验结果对岩石的常规力学参数进行标定。

4）将颗粒间的线性接触模型替换为Burgers接触，保持颗粒间的平行黏结不变。采用fish语言编制流变加载程序，根据试验结果对流变接触模型的微观参数进行标定。

1.2.2 模型验证

基于室内千枚岩三轴压缩试验与单轴流变试验结果［2］对数值模型进行验证。标定得到的细观参数见表1和表2。

表1 千枚岩的岩石基质体弹塑性力学参数

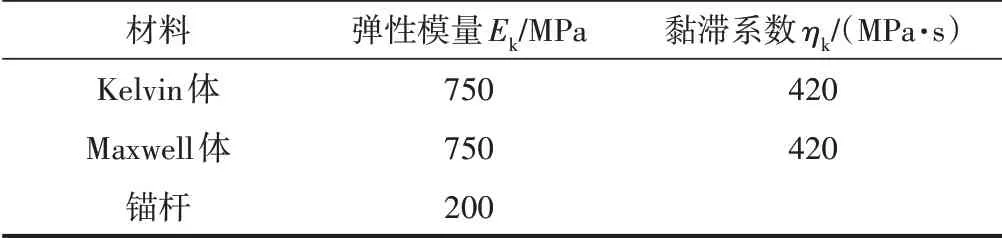
表2 千枚岩流变力学参数

室内试验与数值模拟结果对比见图1。可知，试验结果与模拟结果吻合较好。这表明所建立的层状岩体流变模型可反映岩石的各向异性流变特性。

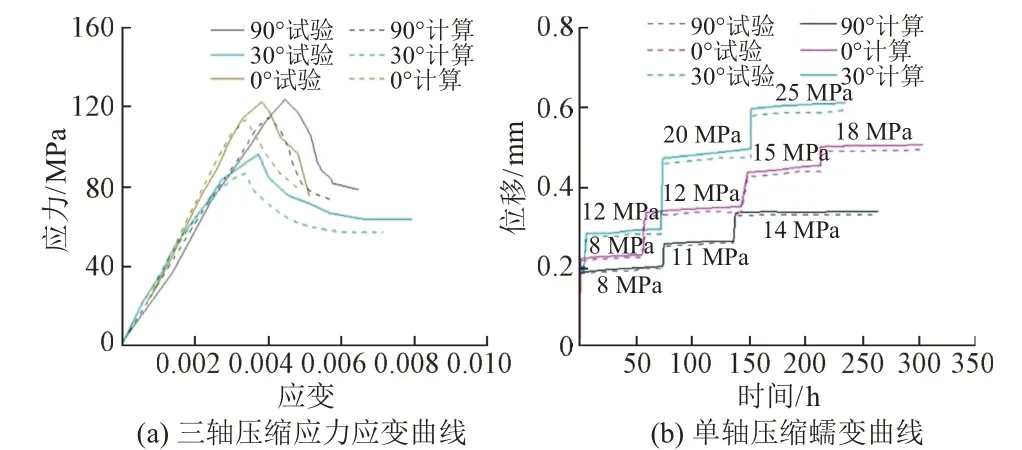
图1 室内试验与数值模拟结果对比

2 数值模型的建立

建立离散-耦合数值模型（图2），尺寸为70 m×70 m。中部开挖影响区域（35 m×35 m）选取颗粒离散体表征围岩，影响区外侧的岩体用有限差分网格表征。离散颗粒直径平均为6.8 cm，短时与流变力学参数参见表1和表2。有限差分网格的流变效应采用Burgers模型表征，参数同表2。

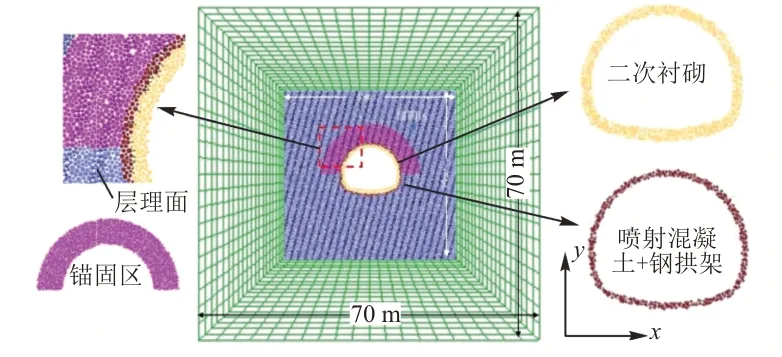
图2 数值模型

支护体系中的二次衬砌、喷射混凝土与钢支撑组成的复合体均采用BPM模拟。喷射混凝土与钢支撑复合体的整体弹性模量［15］为

式中：E为等效弹性模量；E0为喷射混凝土弹性模量；Ag为钢支撑的截面积；Eg为钢支撑的弹性模量；Sc为喷射混凝土的截面积。

支护结构的微观力学参数见表3。

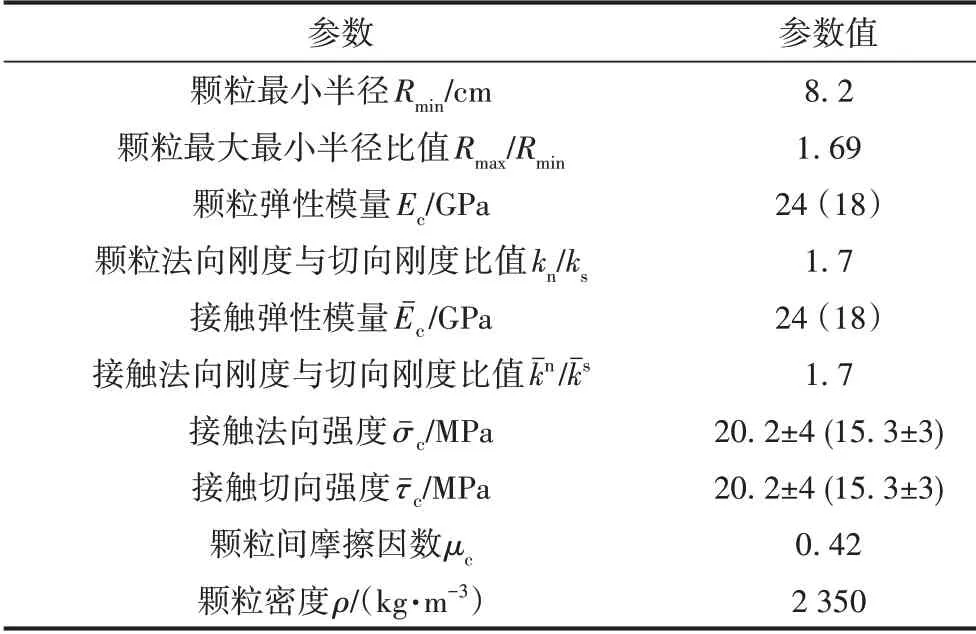
表3 二次衬砌、喷射混凝土及钢拱架微观力学参数

既有研究结果［16］表明，锚杆可以有效地增加岩体的黏聚力，且对内摩擦角影响较小。因此，假定锚固区岩体的内摩擦角不变，其黏聚力增加为［17］

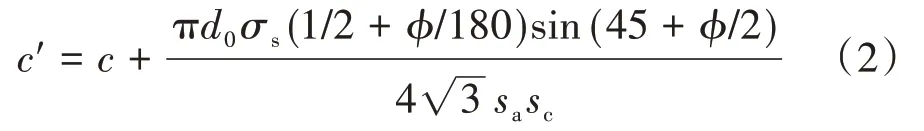
式中：c′为锚固区的等效黏聚力；d0为锚杆直径；σs为锚杆抗拉强度；sa为锚杆轴向布置间距；sc为锚杆环向布置间距。

为揭示地应力场及衬砌背后空洞对衬砌破坏特征的影响规律，选取的计算工况如下。

1）地应力场：①侧压力系数λ=0.5，水平方向应力σx=12 MPa，竖向应力σy=6 MPa；②λ=1.0，σx=σy=8 MPa；③λ=2.0，σx=6 MPa，σy=12 MPa。

2）层理面方向，层理面与水平方向夹角θ=0°、30°、60°、90°。

3）单一空洞：拱顶、左拱肩、左拱腰。

4）双空洞：拱顶与左拱肩，拱顶与左拱腰，左拱肩与左拱腰。

3 计算结果分析

3.1 地应力场的影响

以θ=30°为例，衬砌与围岩完全接触时，二次衬砌不同地应力场下开裂过程见图3。其中，从左往右依次为t=5、15、30、50年，下同。

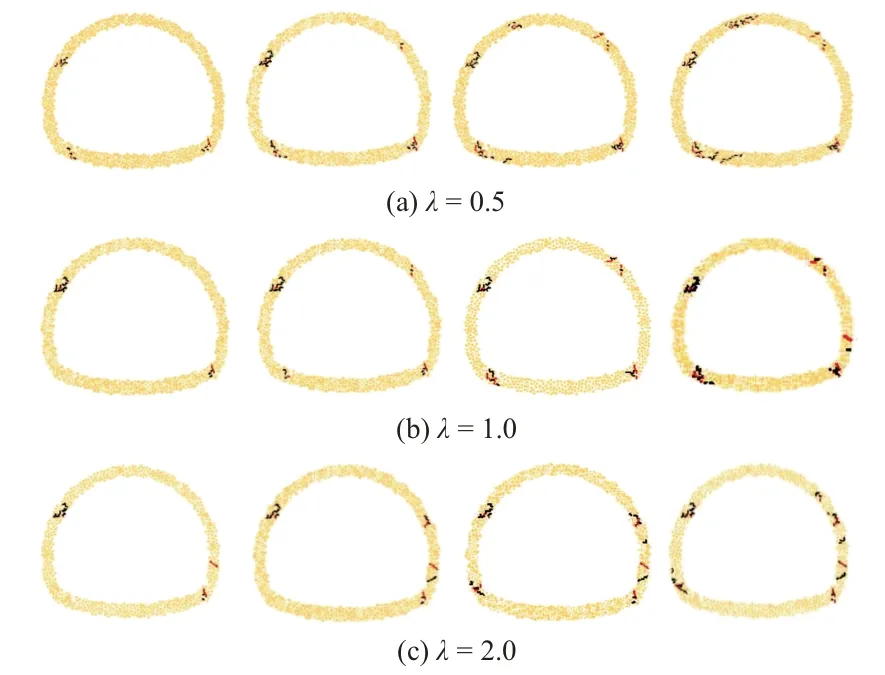
图3 不同地应力条件下衬砌开裂过程

由图3可知：

1）λ=0.5时，裂纹首先出现在左拱肩及左右拱脚（t=5年），随后左拱肩裂损程度增加（t=15年）；t=30年时，左右拱脚进一步开裂，且右拱肩出现少许微裂纹；t=50年时，拱顶出现严重开裂，且左拱脚裂损程度增加。

2）λ=1.0时，左拱肩与右拱脚在t=5年时首先开裂；t=15年时，左拱脚与右拱肩出现少许微裂纹，随后左右拱脚及右拱肩裂损程度不断增加（t=30、50年）。

3）λ=2.0时，左拱肩及右拱脚首先开裂（t=5年）；t=15年时，右拱肩出现少许裂纹，随后左拱脚出现开裂（t=30年）；t=50年时，右拱腰裂损程度增加。

地应力场对二次衬砌的开裂行为有显著影响。当地应力场以水平地应力场为主时，二次衬砌开裂集中出现在拱顶及拱底区域。当地应力场以静水压力场或竖向地应力为主时，二次衬砌开裂分布在左右拱腰区域。以t=15年为例，不同地应力条件下二次衬砌弯矩的分布见图4。可知：λ=1.0时，二次衬砌正弯矩（内侧受拉）分布在与层理面方向垂直的一定范围内（80°～160°与270°～340°）；λ≠1.0时，左右侧正弯矩分布区域中心的连线会向着小主应力方向发生一定程度的偏转。对比图3可知，二次衬砌受力较大的位置也是微裂纹聚集的位置。

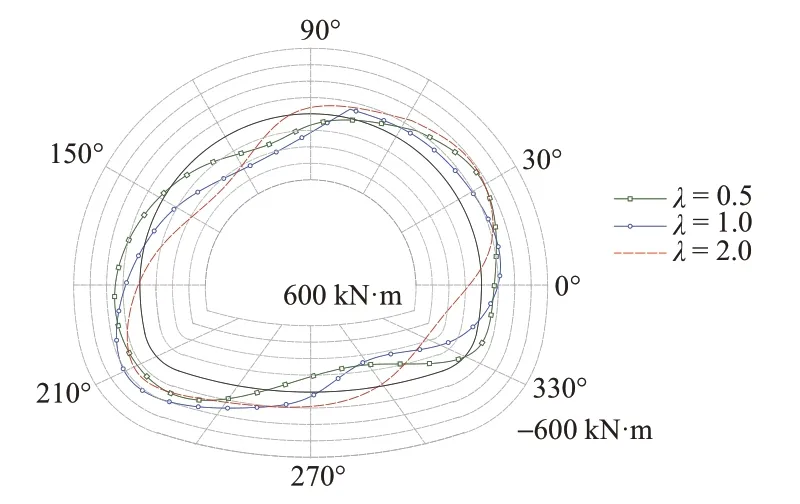
图4 不同地应力条件下二次衬砌弯矩（t=15年）

3.2 层理面倾角的影响

以λ=1.0为例，衬砌与围岩完全接触时，不同层理面倾角条件下二次衬砌的开裂过程见图5。

图5 不同层理面倾角下衬砌开裂过程

由图5可知：

1）θ=0°时，拱顶与右拱脚首先出现零星裂纹（t=5年）；t=15年时，拱顶与右拱脚裂损程度增加，随后左拱脚出现大量裂纹（t=30年）；t=50年时，拱顶与左右拱脚裂损程度增加。

2）θ=60°时，裂纹首先在左拱腰附近产生（t=5年），随后右拱腰附近产生零星开裂（t=15年）；t=30年时，左拱肩开裂，之后右拱肩产生裂纹（t=50年）。

3）θ=90°时，其开裂过程与裂损形态与θ=60°大致相似，不同的是θ=90°时左拱脚裂损程度大于θ=60°时，而右拱腰裂损程度小于θ=60°时。

层理面倾角对二次衬砌的开裂过程及最终裂损形态有较大影响。一般而言，裂纹首先出现在平行于层理面一定范围内的结构内部，且严重开裂区域也分布在平行于层理面一定范围内的结构两侧。不同层理面角度下二次衬砌弯矩分布见图6。可知：θ=0°时，二次衬砌正弯矩分布在拱顶与拱底区域，负弯矩分布在左右拱腰区域；θ=60°时，二次衬砌正弯矩分布在与层理面方向垂直的一定范围内；θ=90°时，二次衬砌正弯矩分布在拱顶、拱底与左右拱腰区域，负弯矩分布在拱肩与拱底区域。可以看出，由于层理面的拉伸与张开效应，与层理面方向垂直的二次衬砌区域在层面开裂产生的挤压作用下，内侧容易产生张拉变形。

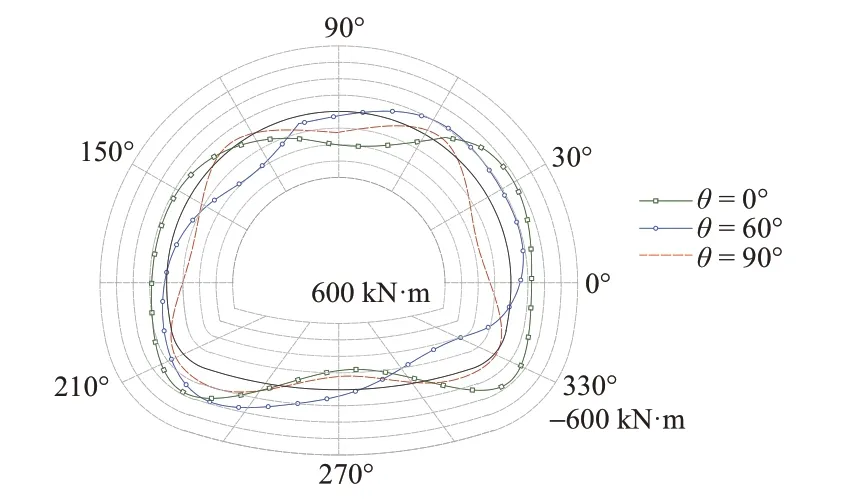
图6 不同地应力条件下二次衬砌弯矩（t=15年）

3.3 空洞的影响

对5 000多座铁路隧道的现场质量检测结果显示，隧道衬砌背后的空洞多发生在拱顶、拱肩与拱腰处［18］。对层状岩体而言，由于层理面的剪切与张拉效应，隧道开挖后围岩易在与层理面垂直的方向出现超挖。因此，综合现场测试统计结果及层状岩体隧道的特征，选取左拱肩、左拱腰与拱顶处空洞加以分析。

当隧道开挖产生超挖以后，会对空洞进行注浆回填。因此，一般情况下二次衬砌背后空洞的体积不会太大。同时，实际空洞的形状为不规则几何体，刘海京［19］认为空洞形状对围岩压力大小及分布规律影响较小，因此计算模型可忽略空洞形状影响。国内外学者也大多将空洞简化为圆形［20-21］。基于现有研究基础，空洞直径取0.6 m。在数值计算中，通过删除图中相应位置半圆内的岩石颗粒，实现对空洞的模拟。

3.3.1 单一空洞

以λ=1.0，θ=30°为例，二次衬砌壁后存在单一空洞时，其裂损过程见图7。

由图7可知：拱顶存在空洞时，裂纹首先出现在拱顶及右拱脚（t=5年），其次出现在左拱脚（t=15年），然后出现在左拱肩，且左拱脚裂损程度增加（t=30年）；t=50年时左拱肩裂损程度增加；左拱肩存在空洞时，其破坏过程及最终破坏形态与无空洞类似；左拱腰存在空洞时，首先是左拱腰与右拱脚出现开裂（t=5年），其次右拱肩出现少许裂纹（t=15年），然后右拱腰裂损程度不断增加（t=30、50年）。

图7 单一空洞条件下衬砌渐进性破坏过程

与图3（b）对比可以看出，空洞对二次衬砌的裂损过程影响较显著。当衬砌壁后单一空洞出现在拱顶或左拱腰时，衬砌裂损演化过程及最终开裂形态与无空洞情况相比差异较大；而当衬砌壁后单一空洞出现在左拱肩时，衬砌裂损演化过程及最终开裂形态与无空洞情况相比差异性较小。同时，由于空洞的存在减弱了空洞附近地层对混凝土形变的约束作用，因此，二次衬砌结构在空洞附近均产生了开裂。

t=15年时单一空洞下二次衬砌的弯矩见图8。可知，由于空洞附近的二次衬砌没有围岩的约束作用，在两侧围岩挤压荷载的作用下，空洞附近的二次衬砌断面容易产生沿着空洞方向的变形，即结构外侧受拉。

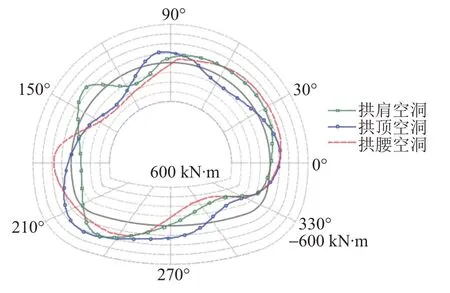
图8 单一空洞条件下二次衬砌弯矩（t=15年）

3.3.2 双空洞

以λ=1.0，θ=30°为例，双空洞条件下，空洞对二次衬砌开裂过程的影响见图9。可知：当拱顶及左拱肩存在空洞时，由于左拱肩空洞对衬砌开裂行为影响较小，因此其衬砌裂损行为与单一拱顶空洞相似；当左拱肩及左拱腰存在空洞时，衬砌开裂过程与仅存在左拱肩空洞类似；当拱顶与左拱腰存在空洞时，裂纹首先出现在拱顶、左拱腰及右拱脚（t=5年），随着服役年限增加，拱顶、左拱腰及右拱脚的裂损程度不断增加。

图9 双空洞条件下衬砌开裂过程

不同空洞组合对二次衬砌裂损行为影响显著。拱顶及左拱肩空洞对衬砌开裂的影响与单一拱顶空洞相似。当左拱肩及左拱腰存在空洞时，其衬砌开裂过程与仅存在左拱肩空洞类似。拱顶与左拱腰空洞对衬砌开裂的影响与单一空洞差异明显。同时，各种工况下，空洞附近处的混凝土均出现开裂。

t=15年时双空洞条件下二次衬砌的弯矩分布见图10。可知，在两侧围岩挤压荷载的作用下，空洞附近二次衬砌断面容易产生沿着空洞方向的变形，即结构外侧受拉。这与单空洞条件下相似。

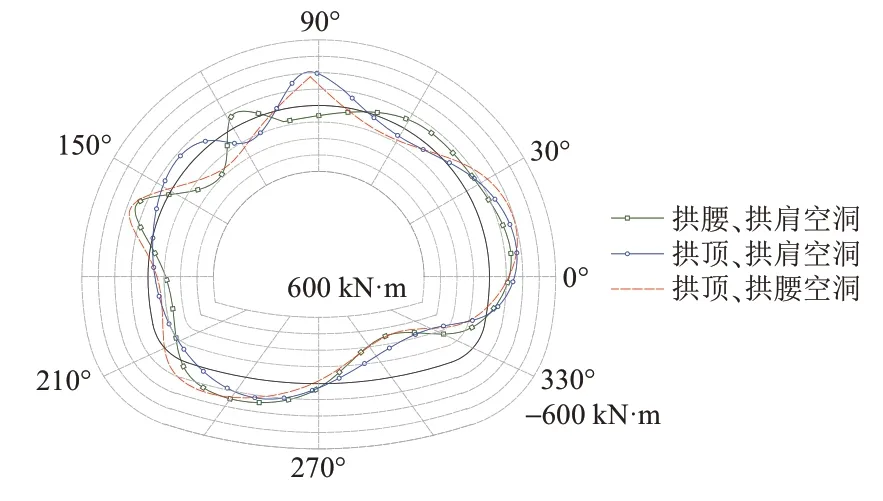
图10 双空洞条件下二次衬砌弯矩（t=15年）

4 结论

1）地应力场对二次衬砌的开裂行为影响显著。当地应力场以水平地应力场为主时，二次衬砌开裂集中出现在拱顶和拱底处。当地应力场以静水压力场或竖向地应力场为主时，二次衬砌开裂分布在左右拱腰处。

2）裂纹首先出现在平行于层理面一定范围内的结构内部，且严重开裂区域也分布在平行于层理面一定范围内的结构两侧。

3）当单一衬砌壁后空洞出现在拱顶或左拱腰时，衬砌裂损演化过程及最终开裂形态与无空洞情况相比差异较大；而当单一衬砌壁后空洞出现在左拱肩时，衬砌裂损演化过程及最终开裂形态与无空洞情况相比差异性较小。

4）由于空洞的存在减弱了空洞附近地层对混凝土形变的约束作用，因此无论衬砌背后是单一空洞还是双空洞，空洞附近处的混凝土均出现开裂。

5）由于层理面的拉伸与张开效应，与层理面方向垂直的二次衬砌区域在层面开裂产生的挤压作用下，内侧容易产生张拉变形。同时，空洞附近二次衬砌均出现面向围岩一侧受拉的情况。