基于流固耦合的破碎围岩隧道应力和位移的非线性解析

孙中华 傅鹤林 崔言继

1.中国建筑第八工程局有限公司，上海 200112；2.中南大学土木工程学院，长沙 410075

在高水压地下环境中开挖隧道会面临地下水渗流的问题，从而影响隧道围岩的应力场和位移场［1］。文献［2-3］探讨了考虑围岩应变软化因素时等效应力的计算方法。文献［4-6］对基于有限元强度折减法的岩土破坏判断准则和工程应用做了研究。文献［7-9］通过数值模拟分析了富水状态下隧道围岩稳定性。文献［10-12］基于流固耦合原理，分析了围岩级别、隧道断面形式、是否渗流三个因素对围岩稳定系数和围岩塑性区分布范围的影响。

针对富水区隧道流固耦合的研究多采用数值模拟，理论研究多集中于开挖稳定后的围岩及结构稳定性，而针对开挖过程中考虑流固耦合因素时隧道应力与位移解的研究鲜有涉及。隧道位于富水区时，围岩的应力场和位移场受渗流场的影响，在富水工况下套用常规情况下隧道围岩的应力解析解，往往和实际差别较大，而且大部分围岩塑性区判定都以线性强度准则作为标准，而实际上围岩强度往往是非线性的，所以在理论上尚需完善。

本文在隧道开挖后地下重分布的应力场基础上，考虑渗流场的影响，并利用非线性强度准则，给出隧道围岩在应力重分布和地下渗流双重影响下的塑性区半径，以期为工程应用提供理论依据。

1 塑性区中的应变位移解析

围岩位移协调方程为

式中：h为剪胀特性参数，h=(1+sinψ)/(1-sinψ)，ψ为剪胀角；u为围岩位移；r为围岩半径；B为参数，B=(1+μ)(σrp-σ0)/E，μ为围岩泊松比，σrp为围岩临界支护力，σ0为围岩的初始地应力，E为围岩弹性模量。

由式（1）解得围岩位移u的表达式为

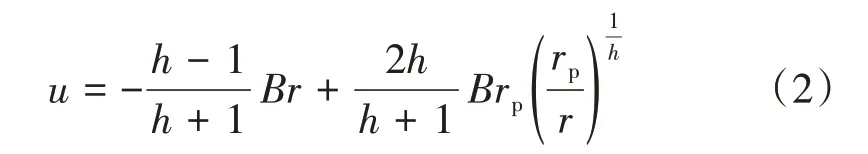
式中：rp为围岩塑性区半径。

进而求得开挖轮廓线位移ur0的表达式为

式中：r0为开挖轮廓线半径。

围岩的径向应变εr和环向应变εθ分别为

2 考虑渗流和应力场重分布的应力解析

2.1 渗流场计算

将半无限地下空间内的深埋隧道附近渗流模型假定为均匀径向渗流，隧道半径为ra，出水面为恒定水头ha，较远处为恒定水头h0，所以水流由外圆均匀流向内圆，在渗透系数不变条件下渗流连续微分方程为

式中：H为地下总水头值。

边界条件为H(r)r=ra=ha，H(r)r→∞=h0。解得［13］

式中：α为水头恒定的半径与隧道半径的比值，根据工程经验可取30。

渗透水压力应为体积力fr，计算式为

式中：ξ为岩石等效孔隙水压力系数；γw为水的重度。

根据微单元受力平衡得到相应的应力微分方程

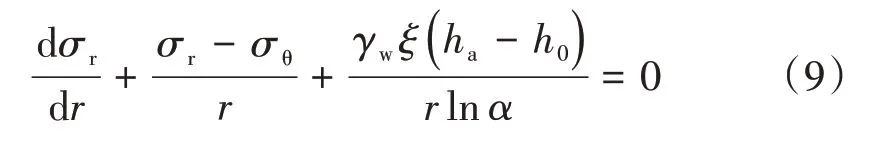
式中：σr为径向有效应力；σθ为切向有效应力。

边界条件为σ(r)r=ra=-pa，σ(r)r→∞=-p0，pa、p0分别为隧道开挖面和围岩无穷远处的径向应力。解得

式中：β为比例系数，取值可与α相同；k1、k2、k3、k4、A1、A2为常数，其值由下列各式确定。

2.2 弹塑性应力解答

围岩在隧道开挖后发生变形，可能进入塑性阶段，从而会出现应力重分布的现象。考虑此因素的影响，引入应力调整系数λ，则径向有效应力σr和切向有效应力σθ的表达式变为

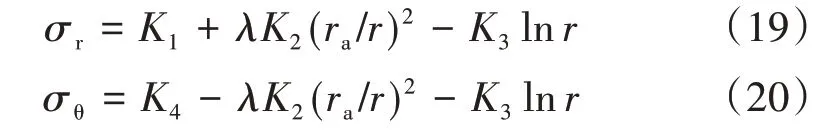
Hoek-Brown强度准则是用于岩石破裂的经验公式，用以定量分析岩体应力状态。将式（19）和式（20）代入Hoek-Brown强度准则，再考虑边界条件σ(r)r=ra=-pa，可得塑性区径向应力σrp和切向应力σθp，其推导如下。

式中：S为半经验参数［14］；a、m、γ为由三轴实验确定的参数。

a=1/2时，塑性区应力满足方程

a=1/2时，可得参数λ的值为

由于在围岩弹性区与塑性区的交界处，必定满足应力连续的条件，所以塑性区半径rp有如下关系式：

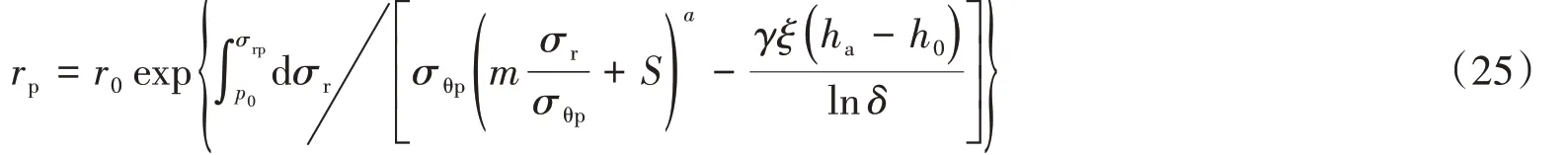
当a=1/2时，可得

因此，当a=1/2时，考虑重力重分布和渗流时的塑性区半径计算公式为

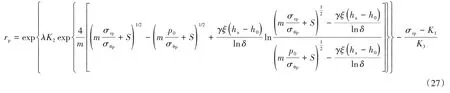
3 参数的影响分析

参考文献［15］，模型各参数取值为ra=2 m，p0=10 MPa，E=2 000 MPa，μ=0.25，内摩擦角φ=35°，黏聚力c=1 MPa，围岩的孔隙水压力系数ξ=1，α=30，β=30。

计算仅考虑渗流场作用下围岩应力与rp/r之间的关系，结果见图1。可知：围岩在地下渗流作用下，应力明显增大，且环向应力受渗流场的扰动比径向应力大；当隧道内水头较大时，渗流影响减小。

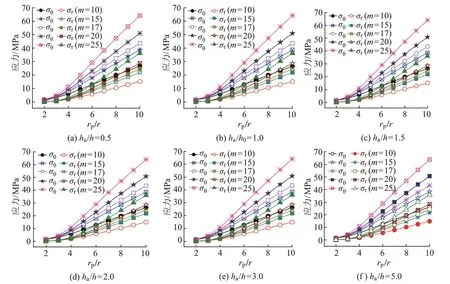
图1 不同水头比下考虑渗流场时的应力场与r p/r之间的关系

在渗流的基础上考虑围岩塑性变形而受力重分布时，计算围岩应力与rp/r之间的关系，结果见图2。可知，相比于纯渗流作用，在同时考虑地下渗流和部分围岩塑性变形时，塑性区范围内的围岩切向应力增大，而径向应力会有一定的减小。

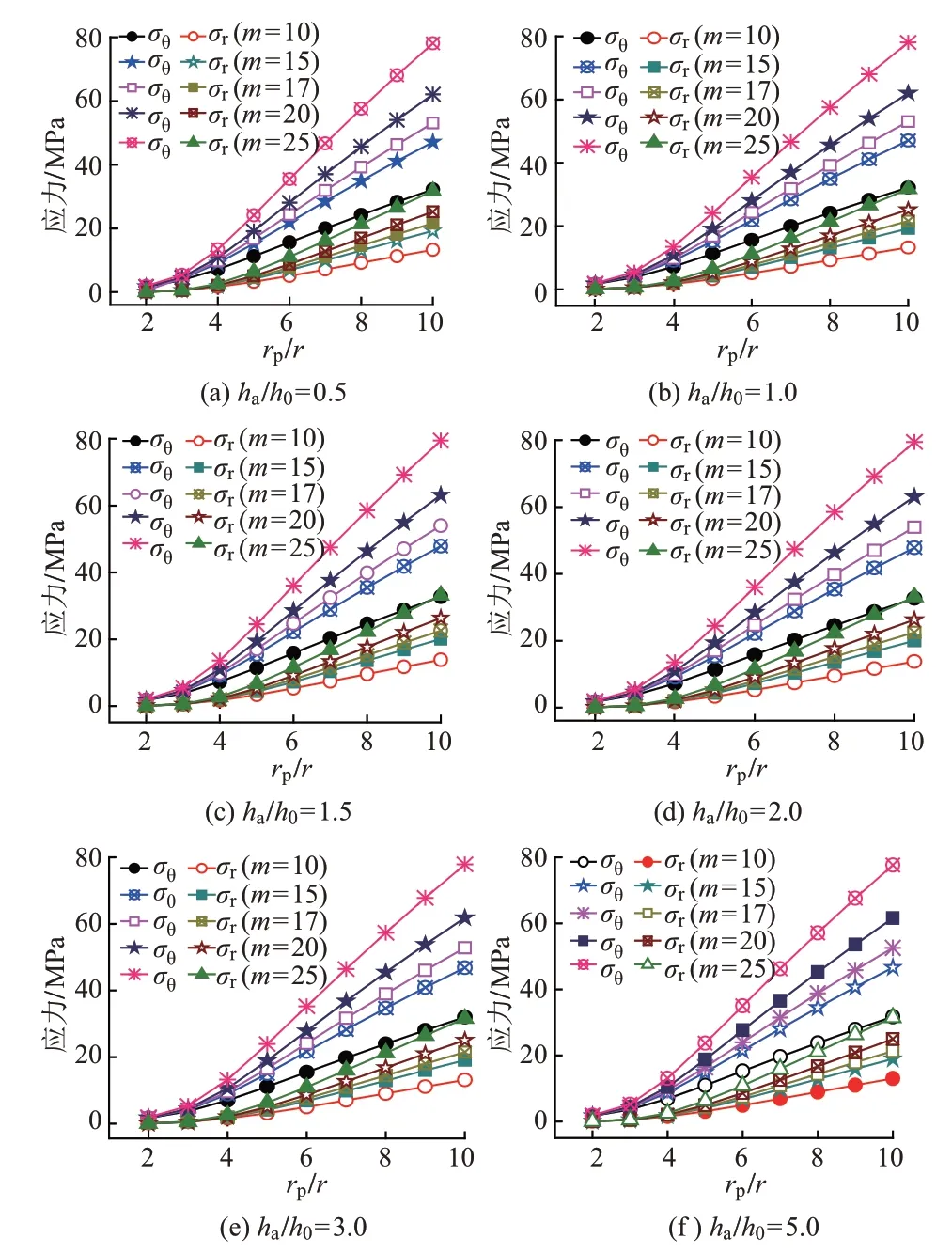
图2 考虑应力重分布和渗流场时的应力场与r p/r之间的关系

渗流是由于地下无限远处与隧道面的水头差造成的，所以可以用ha/h0来表征渗流的特征。ha/h0值越小，渗流作用越明显。通过多工况计算研究了围岩塑性区半径随ha/h0的变化规律，结果见图3。此外，还分析了表征围岩条件的参数m对塑性区范围的影响，见图4。

图4 塑性区半径与m的关系

由图3可知，随着ha/h0值变大，塑性区半径逐渐减小，可以看出渗流对塑性区具有明显的影响，隧道围岩水位差越大，渗流引起的渗透力越大，围岩塑性变形的范围也越大。

图3 塑性区半径与h a/h0的关系

由图4可知，除了地下渗流外，围岩的力学参数也对塑性区半径有明显的影响，且不同水头差条件下的塑性区半径变化规律一致，说明地下渗流和参数m对塑性区范围的影响相对独立，围岩级别越大，则塑性区半径越小。

除了渗流影响外，还应当考虑围岩应力重分布的影响。此时，rp与ha/h0以及与m的关系见图5和图6。

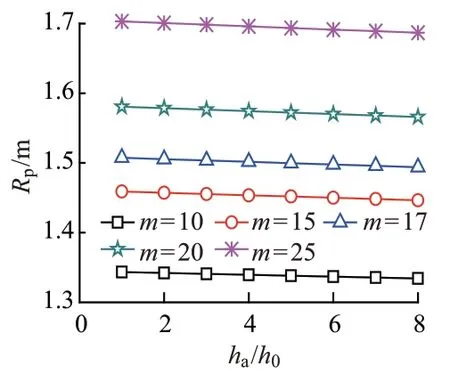
图5 r p与h a/h0的关系

图6 r p与m和h a/h0的关系

由图5和图6可知，相对于仅考虑渗流作用，在引入应力重分布后，塑性区半径出现一定程度上的减小，且rp与m呈现线性关系，而不是仅考虑渗流工况下的非线性（参考图4）。

4 算例验证

对不同m和ha/h0工况下的塑性区半径rp进行计算，结果见表1。Fenner理论值为2.8。表1表明，在考虑地下渗流和应力重分布时，本文所提的塑性区半径非线性解析解比Fenner理论解要大，充分证明了渗流场和应力重分布对围岩变形的影响，比Fenner解符合实际，且当m减小时即围岩等级较好，则该影响也减小，结果也更趋近于Fenner理论解，说明了本文所提方法的正确性。

表1 本文塑性区半径r p的计算结果

5 结论

1）在地下渗流的作用下，围岩切向应力和径向应力均有增大，且切向应力所受到的扰动更为明显。

2）在渗流的基础上，引入应力重分布的因素，发现塑性区范围内的围岩切向应力增大，而径向应力有所减小。

3）地下渗流和应力重分布均会导致围岩塑性区半径增大，反映围岩质量的m值越大则影响越大，当隧道与地下原位水头差越大，影响也越大。