基于修正的SRK 状态方程预测纳米孔中二元流体的界面张力
吕建荣 丁振华 张德富 王晓光 聂振荣
(中国石油新疆油田分公司勘探开发研究院; 新疆克拉玛依 834000)
0 引 言
页岩油气和致密油气具有重要的开采价值[1-2]。 与常规的油气藏相比, 页岩储层和致密储层的孔隙达到纳米级, 在纳米孔内的受限流体的界面张力(IFT) 不同于常规的体积流体。 因此, 建立预测纳米孔中油气界面张力模型, 对页岩油气和致密油气勘探开发具有重要意义。
付东等[3]基于二阶微扰理论建立状态方程(EoS) 模型, 并结合密度泛函理论, 研究不同量程参数的Yukawa 流体的界面张力. 李小森等[4]基于基础度量理论, 密度泛函理论和一阶平均球近似理论建立Lennard-Jones (LJ) 流体自由能模型,研究汽液平衡时的界面张力。 曾志勇等[5]基于状态方程和毛细管Kelvin 模型, 建立甲烷水合物和二氧化碳水合物界面张力预测模型。 近年来, 许多学者研究受限流体的临界属性移位现象[6]。 Zhang等[7]基于修正的Peng-Robinson (PR) EoS, 提出一种递减界面张力法计算最小混相压力。 Zhang 等[8]基于van der Waals (vdW) EoS 和受限流体临界温度和压力移位建立一个半解析状态方程。 Zhang等[9]将Travalloni 等[10]提出的纳米孔吸附理论引入到状态方程中, 并推导预测吸附厚度的经验关联式。 Zhang 等[11]设计纳米实验装置并测量在纳米孔中的界面张力, 同时提出计算纳米孔中界面张力的理论方法。
页岩包含有矿物孔及有机孔等复杂孔隙类型,在状态方程模型中, 所有孔隙类型均假设为圆柱孔[8]。 因此, 孔隙对模型的影响简化成孔隙半径对模型预测结果的影响。 Jin 等[12]将孔隙分为三种类型: 孔隙尺寸大于10 nm, 孔隙中的吸附作用很弱且可以忽略, 孔隙中流体是均匀的, 常规的状态方程能够描述流体的相行为; 孔隙尺寸小于等于10 nm, 孔隙中有很强的吸附作用, 孔隙中流体是非均匀的, 常规的状态方程不能用于非均匀体系,应该采用分子模拟方法,例如蒙特卡洛模拟;最后一种类型是分子移向干酪根。 Tan 等[13]的研究表明,状态方程不能描述孔隙中流体的吸附过程。 本文针对孔隙尺寸大于10 nm 的均匀流体,只考虑流体之间的相互作用,忽略分子—孔隙之间的相互作用。
本文基于修正的SRK 状态方程和修正的vdW混合规则, 建立一个预测纳米孔中油气界面张力的状态方程模型, 该模型能描述纳米孔中孔隙半径和分子—分子间相互作用的影响。 将状态方程与等张比容模型结合, 建立基于气液相平衡的界面张力计算模型, 并提出具体计算方法。 建立的SRK 模型的预测结果与vdW 模型[11]和实验数据进行对比分析。 同时, 分析压力、 温度和孔隙半径对流体界面张力的影响。 准确计算纳米孔内流体的界面张力在油田勘探开发中具有重要作用, 如注二氧化碳提高采收率过程中, 准确计算界面张力是合理设计注入参数的重要条件之一, 此外, 界面张力还可作为混相判据, 是混相驱的重要参数之一; 在油藏数值模拟过程中, 准确的状态方程提高组分模拟的精度,并被广泛地运用于注二氧化碳驱模拟。
1 热力学模型
1.1 修正的状态方程
流体在纳米孔中受到限制, 分子—分子相互作用由Lennard-Jones 势能描述, 基于统计热力学的巨正则配分函数, Zhang 等[8,9]修正临界温度和压力位移关联式, 并建立半解析的Soave-Redlich-Kwong (SRK) EoS
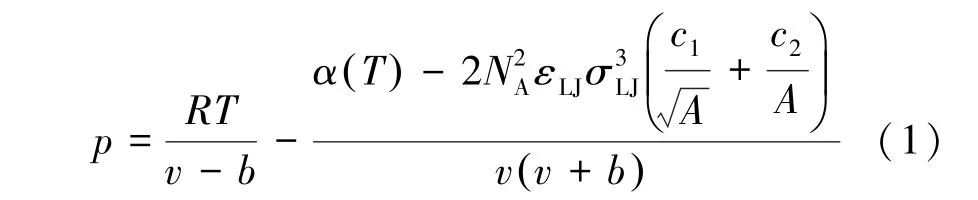
式中:p——系统压力, MPa;
T——系统温度, K;
R——通用气体常数, 等于k·NA;
k——玻尔兹曼常数, 1.38 × 10-23J/K;
NA——阿伏伽德罗常数, 6.022 140 76×1023mol-1;
v——摩尔体积, cm3/mol;
εLJ、σLJ——分子间的Lennard-Jones 能量和尺寸参数;
A=π· (rp/σLJ)2;
rp——孔隙半径, cm;
c1= 3.562 2;
c2=-0.664 9[8];
α(T)、b——修正的SRK 状态方程参数,由常规的SRK 参数[8]延伸到纳米孔中得:

式中:Tc,p——在纳米孔中的临界温度, K;
Tr,p——对比温度, 等于T / Tc,p;
pc,p——在纳米孔中的临界压力, MPa;
ω——偏心因子。
Zhang 等[8]对临界压力和温度移位计算公式进行修正, 其计算表达式为:
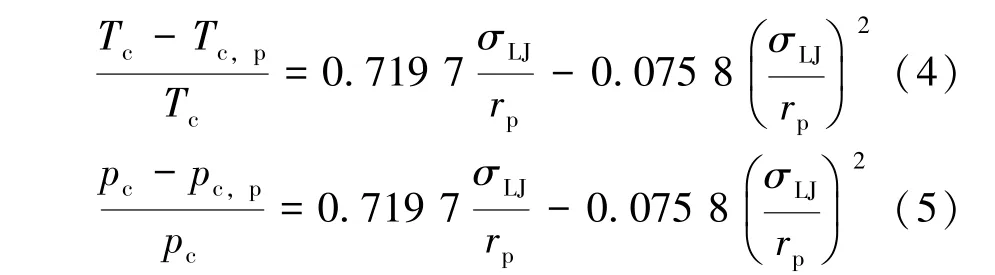
式中:Tc——临界温度, K;
pc——临界压力, MPa。
常规的vdW 一流体混合规则[14-15]为:
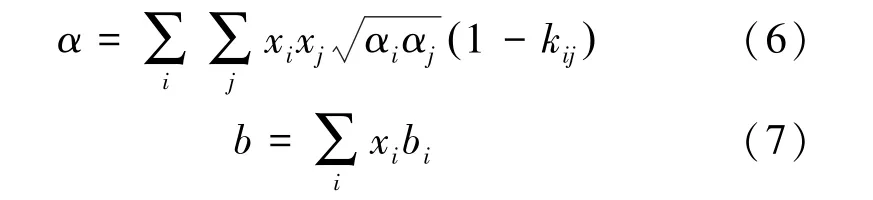
式中:xi——i组分的摩尔分数;
kij——i组分与j组分的相互作用参数。
常规的Berthelot-Lorentz 混合规则[16]为:
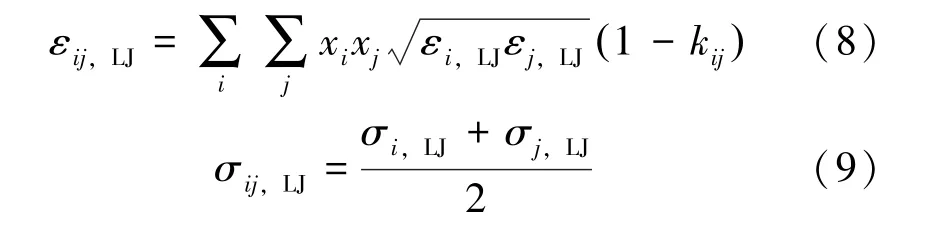
为了简化模型, 笔者将式(6) 和(8) 中的kij取相等的值。 将vdW 混合规则修正为:

1.2 逸度系数
相平衡计算是基于每个组分在气液相中的逸度相等, 即

pL、pV——液相、 气相压力, MPa;
yi——第i个组分的气相摩尔分数。
状态方程和逸度系数均可由巨正则配分函数导出, SRK 状态方程的逸度系数(推导方法参考文献[8-9] ) 为:


式中Z——偏差因子。
1.3 计算方法
状态方程计算气液平衡采用牛顿迭代法[8]。在储层条件下, 由于毛管压力的影响, 气液相压力是不相等的。 笔者将液相和气相分别考虑成润湿相和非润湿相[17]。 因此, 毛管压力和气相压力为:
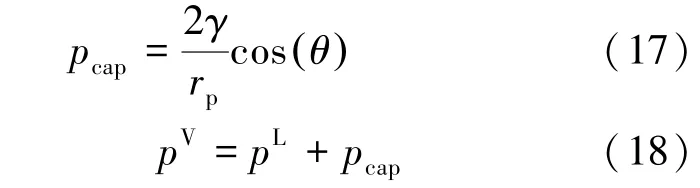
式中:pcap——毛管压力, MPa;
γ——界面张力, mJ/m2;
θ——接触角, 文献[8] 实验结果建议近似为30°。
Weinaug 等[18]提出界面张力(界面张力与气液相组成有关) 计算方法为

式中:ρL、ρV——液相、 气相的摩尔密度,mol/cm3;
pi——i组分的等张比容, 由Nobakht 等[19]的方程计算:
p= 176.050 05- 7 472.980 7Vc-0.874 580 88Tc+ 1 560.479 3H+ 19.309 439H2+
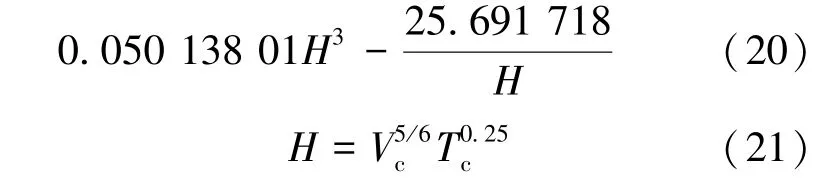
式中:Vc——摩尔临界体积, dm3/mol;
H——Tc和Vc的函数。
主要的计算步骤:
(1) 输入p—T—x—rp条件, 用式(4) 和式(5) 计算临界温度和临界压力移位, 用Wilson 方程[9]计算初始平衡常数K值(采用Wilson 方程求解, 数值为0.2~1.5), 假设初始气相压力等于液相压力;
(2) 用Rachford-Rice 方程[20]计算xi和yi, 使用混合规则(式(7) 和式(10) ) 计算SRK EoS的混合物参数。 用式(1) 计算气液相的摩尔体积(v), 气液相摩尔密度是摩尔体积的倒数;
(3) 用式(19) 计算界面张力, 式(19) 中的等张比容由式(20) 和式(21) 计算得到, 然后用式(17) 和式(18) 分别计算毛管压力和气相压力。 用式 (15)、 式 (16) 和式 (13)、 式(14) 计算气液相逸度系数和气液相逸度;

2 界面张力
Zhang 等[11]设计出纳米实验装置, 并测量甲烷-正葵烷(C1-nC10) 和氮气-正葵烷(N2-nC10)混合物在纳米孔(rp= 50 nm) 中的界面张力, 其具体测量值见表1。 对比实验测量的界面张力与模型预测值, 是检验建模正确性的重要方法之一。 因此, 笔者对不同温度下的C1-nC10和N2-nC10混合物的界面张力进行预测, 其使用到的纯组分状态方程参数列于表2。

表1 C1-nC10和N2-nC10混合物在298.15 K、 326.15 K 下的纳米孔中测量和模型预测的界面张力(IFT)Table 1 Interfacial tensions (IFT) of C1-nC10 and N2-nC10 mixtures measured and predicted at the temperatures of 298.15 K and 326.15 K in nanopores

表2 本文使用的纯物质状态方程参数[9]Table 2 Parameters of the EoS of the pure substances used in this paper[9]
3 结果与讨论
基于以上所建模型, 对Zhang 等[11]测量的界面张力数据进行预测, 模型预测值见表1, 并与vdW 模型[11]进行对比分析。
图1 给出了SRK EoS 模型(对于非极性组分,二元相互作用参数kij通常为0,kij为零表明模型不需要额外拟合二元混合物实验数据, 模型具有较好的预测能力) 和vdW EoS 模型[11]在不同条件下对C1-nC10混合物的界面张力预测结果, 由图1 可知:随着压力的升高, C1-nC10混合物在298.15 K (图1(a) ) 和326.15 K (图1 (b) ) 下的纳米孔中的界面张力逐渐减小, SRK 和vdW 模型均能准确地预测界面张力; 通过SRK 模型对体积相 (rp=1 cm)和纳米孔中的界面张力预测表明, 在相同的温度压力条件下, 体积相中的C1-nC10混合物界面张力大于纳米孔中的界面张力, 即随着孔隙变小,混合物的界面张力逐渐减小。图2 给出了SRK EoS 模型(二元相互作用参数kij=0) 和vdW EoS 模型[11]在不同条件下对N2-nC10混合物的界面张力预测结果, 由图2 可知: 随着压力的升高, N2-nC10混合物在298.15 K (图2 (a) )和326.15 K (图2 (b) ) 下的纳米孔中的界面张力逐渐减小, SRK 和vdW 模型均能准确地预测界面张力; 通过SRK 模型对体积相和纳米孔中的界面张力预测表明, 在相同的温度压力条件下, 体积相中的N2-nC10混合物界面张力大于纳米孔中的界面张力, 即随着孔隙变小, 混合物的界面张力逐渐减小。
表1 列出了SRK EoS 模型(二元相互作用参数kij= 0) 和vdW EoS 模型[11]在不同条件下对C1-nC10和N2-nC10混合物的界面张力计算结果, 计算值是满足相平衡条件(逸度相等) 的模型预测的界面张力, 是系统在热力学平衡时的模型预测结果, 该预测结果与标准值(实验测量结果) 对比分析, 可以分析模型预测的准确程度。
计算值与测量值的平均绝对相对偏差(AARD) 的计算公式为
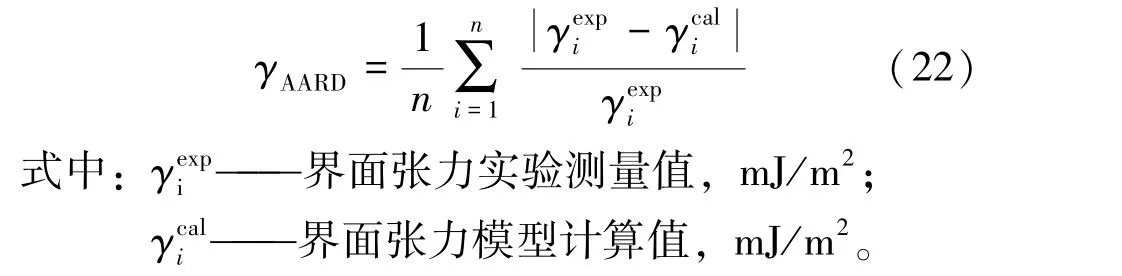
γAARD越小表明预测结果越准确,γAARD一般不超过20.00%。


由表1 可知: SRK 和vdW 模型均能准确地预测界面张力, 但SRK 模型的计算结果更准确。 在298.15 K 和326.15 K, SRK 模型计算的C1-nC10体系的平均绝对相对偏差为12.42 %和7.11 %, 而N2-nC10体系为2.83 %和3.85 %。 vdW 模型计算的C1-nC10体系的平均绝对相对偏差为17.10 %和4.24 %, 而N2-nC10体系为3.98 %和7.53 %。
为了研究界面张力随孔隙的变化关系, 图3 给出了SRK EoS 模型(二元相互作用参数kij= 0)在不同孔隙大小下(rp=10, 30, 100、1 000 nm)对C1-nC10混合物界面张力预测结果,由图3 可知:在相同温度(326.15 K)下,随着孔隙变小,混合物的界面张力逐渐减小,且在较低的压力下,孔隙半径越小,界面张力的减小程度越大,在较高的压力下,由于界面张力比较小,孔隙半径的影响也较小。
图4 给出不同温度下SRK EoS 模型(二元相互作用参数kij= 0) 对C1-nC10混合物的界面张力预测结果(压力为5 MPa)。 由图4 可知: 在相同的压力和孔隙半径下, 随着温度升高, 混合物的界面张力逐渐减小, 在较高的温度下, 界面张力减小程度增加; 在相同的温度和压力下, 孔隙半径越小, 界面张力的减小程度越大, 界面张力越小。
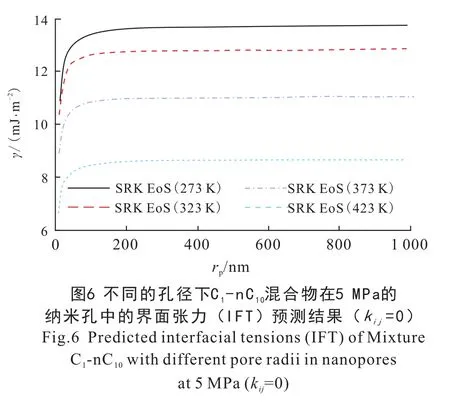
图5 和图6 给出不同孔径下SRK EoS 模型(二元相互作用参数kij= 0) 对C1-nC10混合物的界面张力预测结果。 由图5 和图6 可知: 在相同的温度压力下, 孔隙半径越小, 界面张力的减小程度越大, 界面张力越小; 当孔径大于50 nm 时, 随着孔径的增加, 界面张力几乎不变, 表明孔隙对流体的影响几乎可以忽略。

4 结 论
(1) 基于修正的SRK 状态方程和修正的vdW混合规则, 建立一个预测纳米孔中油气界面张力的状态方程模型, 该模型能描述纳米孔中孔隙半径和分子—分子间相互作用的影响。
(2) 与vdW 模型和实验数据对比表明: 在相同的温度下, 随着压力的升高, C1-nC10和N2-nC10混合物在纳米孔中的界面张力逐渐减小, SRK 和vdW 模型均能准确地预测界面张力。
(3) 通过SRK 模型对体积相和纳米孔中的界面张力预测表明: 在相同的温度压力条件下, 体积相中的C1-nC10和N2-nC10混合物界面张力大于纳米孔中的界面张力。 对不同孔隙半径的纳米孔中的界面张力预测表明: 随着孔隙半径的减小, 混合物的界面张力逐渐减小, 且在较低的压力下, 孔隙半径越小, 界面张力的减小程度越大, 而在较高的压力下, 由于界面张力比较小, 孔隙半径的影响也较小。
(4) 在相同的压力和孔径下, 随着温度升高,混合物的界面张力逐渐减小, 在较高的温度下, 界面张力减小程度增加。 在相同的温度和压力下, 孔隙半径越小, 界面张力的减小程度越大, 界面张力越小。
(5) 在相同的温度压力下, 孔隙半径越小,界面张力的减小程度越大, 界面张力越小; 当孔径大于50 nm 时, 随着孔径的增加, 界面张力几乎不变, 表明孔隙对流体的影响几乎可以忽略。
(6) SRK 模型能准确地预测纳米孔中的界面张力, 为预测纳米孔中油气界面张力提供了一种新思路。

