松辽盆地东南隆起区上白垩统青山口组油页岩有机碳含量预测及效果评价

唐佰强 刘招君 孟庆涛 张朋霖 李元吉 王君贤

（1. 吉林大学地球科学学院， 吉林长春 130061； 2. 吉林省油页岩与共生能源矿产重点实验室， 吉林长春 130061）

0 引 言

油页岩的有机碳含量（w（TOC） ） 及含油率的实验分析测试费时、 费力、 成本高昂， 国内外学者对大区域内的油页岩评价常用测井响应特征进行w（TOC）预测， 包括定性预测、 半定量预测和定量预测。 定量预测主要是建立有机碳含量测井预测模型， 可以分为ΔlgR模型、 多元逐步回归模型和BP 神经网络模型3 类。

（1） ΔlgR模型。 Q. R. Passey 等［1］提出了ΔlgR模型计算烃源岩的w（TOC）， 该方法被众多学者引用、 改进并取得了不错的效果； 朱振宇等［2］使用ΔlgR模型对塔里木盆地烃源岩有机碳含量进行了预测并分析了优缺点； 郭泽清等［3］使用ΔlgR模型预测了柴达木盆地三湖地区第四系烃源岩有机碳含量； 高岗等［4］使用ΔlgR模型对北部湾盆地涠西南凹陷流沙港组湖相优质烃源岩有机碳含量进行预测； 夏宏泉等［5］使用ΔlgR模型对四川盆地长宁地区下志留系龙马溪组烃源岩有机碳含量进行预测； 刘超［6］通过优化K值并引入密度测井曲线提出变系数ΔlgR模型且将其应用在松辽盆地；胡慧婷等［7］对ΔlgR模型的公式推导改进， 避免了读取基线的繁琐， 并通过松辽盆地与海拉尔盆地的烃源岩分析提出了改进的ΔlgR模型； 张鹏飞等［8］使用改进ΔlgR模型渤海湾盆地东营凹陷烃源岩有机碳含量进行预测。

（2） 多元逐步回归模型。 多元逐步回归模型是多元回归模型的发展。 J. D. Mendelson 等［9］将w（TOC） 与声波时差、 中子孔隙度、 密度、 自然伽马之间建立多元回归关系并进行烃源岩w（TOC）预测； 陈浩等［10］以多元回归模型对银额盆地居延海坳陷w（TOC）分布进行了预测； 胡慧婷等［5］通过从多个测井参数中选择w（TOC） 的敏感参数建立了烃源岩w（TOC）的多元逐步回归预测模型。

（3） BP 神经网络模型。 BP 神经网络模型是人工神经网络模型中使用最广泛的模型之一。 王贵文等［11］使用BP 神经网络模型对塔里木盆地台盆区寒武系—奥陶系烃源岩进行了w（TOC）预测；L. M. Johnson等［12］使用BP 神经网络模型对澳大利亚坎宁盆地烃源岩w（TOC） 进行了预测并取得较好效果； 蒋德鑫等［13］对珠江口盆地陆丰凹陷文昌组烃源岩w（TOC） 建立多元回归模型、 BP 神经网络模型和曲线叠合模型， 并分析了3 种模型的预测效果及适用条件。

松辽盆地具有丰富的页岩油资源， 占中国页岩油总量的45%［14］， 矿层分布广泛、 产状稳定、 单层厚度大、 垂向连续性强， 尚未进行商业化开发，极具资源前景［15-16］。

前人对松辽盆地油页岩有机碳含量和含油率进行了定量预测。 如贺君玲等［17］将自然伽马曲线和电阻率曲线叠合建立了ΔlgR模型预测松辽盆地南部油页岩的有机碳含量； 刘博［18］分析测井曲线与有机碳含量关系建立了多元回归模型预测油页岩的有机碳含量； 尚未见到用BP 神经网络模型预测松辽盆地油页岩的有机碳含量的报道。

本文以松辽盆地东南隆起区上白垩统青山口组油页岩为例， 以JFD-1 井、 JFD-5 井青山口组的实测w（TOC） 数据和测井响应数据建立东南隆起区上白垩统青山口组油页岩的改进ΔlgR模型、 多元逐步回归模型和BP 神经网络模型， 并用模型预测JFD-8 井青山口组油页岩的有机碳含量， 通过对比分析JFD-8 井的实测w（TOC） 和预测w（TOC）的误差来讨论3 种模型的适用条件， 为松辽盆地油页岩勘探开发提供了有力的技术支持。

1 地质概况

松辽盆地处于中国东北部， 可划分为6 个一级构造单元： 北部倾没区、 西部斜坡区、 中央坳陷区、 东北隆起区、 东南隆起区和西南隆起区。 沉积层系始于侏罗系， 以白垩系为沉积主体， 上白垩统青山口组和嫩江组是盆地内油页岩主要发育层系［19］。 本文样品来源于东南隆起区的JFD-1 井、JFD-5 井和JFD-8 井（图1）， 取样段为上白垩统青山口组青一段。

东南隆起区青山口组发育深湖—半深湖沉积。以灰色泥岩、 深灰色泥岩、 深灰色油页岩为主， 夹少量薄层泥灰岩和含介形虫灰岩， 局部黄铁矿富集［20］。 青山口组从下至上依次为青一段、 青二段、青三段。 青二段、 青三段油页岩不发育。 青一段油页岩厚度较大， 由岩心观察可知JFD-1 井、 JFD-5井和JFD-8 井平均累计厚度为20.18 m， 最大单层厚度为5.8 m， 常与暗色泥岩互层。 有机质的干酪根类型为Ⅰ—Ⅱ1型， 最大热解峰温度小于435 ℃，处于未成熟阶段， 生油潜力巨大［21-22］。

2 测试样品及实验方法

测试样品均取自于JFD-1 井、 JFD-5 井和JFD-8井青一段， 取心完整， 测井资料包括自然伽马、 电阻率、 声波时差、 密度。 本次研究共有160 块岩心进行了有机碳含量测试， 其中JFD-1 井分析了75组、 JFD-5 井分析了47 组、 JFD-8 井分析了38 组，样品岩性主要为灰色泥岩、 深灰色泥岩、 深灰色油页岩、 泥灰岩、 含介形虫灰岩等。

实测w（TOC） 即经过5%稀盐酸处理后， 通过Leco CS-230 碳硫仪测定有机碳含量。 本文的实测w（TOC） 数据在使用前对岩心深度与测井曲线深度都进行了归位， JFD-1 井岩心深度增加0.82 m、JFD-5 井岩心深度减少0.15 m、 JFD-8 井岩心深度增加0.58 m。

3 测井模型建立

3.1 测井响应特征

松辽盆地东南隆起区青山口组油页岩的测井曲线具有高自然伽马、 高电阻率、 高声波时差和低密度的特点。 东南隆起区青山口组油页岩实测w（TOC）与测井曲线关系见图2。

3.1.1 自然伽马

东南隆起区青山口组油页岩自然伽马测井值主要为124.03 ～253.65 API， 平均值为155.80 API。泥岩自然伽马测井值为114.46 ～146.95 API， 平均值为128.47 API。 油页岩自然伽马测井值明显高于泥岩。 油页岩自然伽马与实测w（TOC） 呈正相关（图2 （a） ）， 相关系数为0.384 4。

3.1.2 电阻率

东南隆起区青山口组油页岩电阻率测井值主要为5.83～30.31 Ω·m， 平均值为10.80 Ω·m。 泥岩电阻率测井值为4.84 ～6.10 Ω·m， 平均值为5.58 Ω·m。油页岩电阻率测井值明显高于泥岩。油页岩电阻率与实测w（TOC） 呈正相关， 相关系数为0.486 6 （图2 （b） ）。

3.1.3 声波时差

东南隆起区青山口组油页岩声波时差测井值主要为378.90～451.43 μs／m，平均值为425.47 μs／m 。泥岩的声波时差测井值为408.94～434.21 μs／m，平均值为418.70 μs／m。 油页岩的声波时差测井值明显高于泥岩。 油页岩的声波时差测井值与实测w（TOC） 呈正相关 （ 图 2 （ c） ）， 相关系数为0.492 3。

3.1.4 密度

东南隆起区青山口组油页岩密度测井值主要为2.02～2.45 g／cm3， 平均值为2.25 g／cm3。 泥岩密度测井值为 2.31 ～2.42 g／cm3， 平均值为2.35 g／cm3。油页岩密度测井值低于泥岩。 油页岩密度测井曲线与实测w（TOC） 呈负相关（图2 （d） ），相关系数为0.758 1。

3.2 预测模型

以松辽盆地东南隆起区JFD-1 井和JFD-5 井的上白垩统青山口组油页岩的实测w（TOC）和测井数据分别建立改进ΔlgR模型、 多元逐步回归模型和BP 神经网络模型， 利用模型分别计算JFD-8 井的预测w（TOC）， 以JFD-8 井的实测w（TOC） 和预测w（TOC） 的误差分析评价3 种预测模型的适用条件。

3.2.1 改进ΔlgR模型

ΔlgR模型是由Q. R. Passey 等［1］提出的使用测井曲线预测不同成熟度条件下的有机碳含量的定量计算方法。 通过将对数坐标的电阻率曲线与算术坐标的声波时差曲线叠加， 以非烃源岩段调准基线计算幅度差ΔlgR。 该方法需要设定有机碳背景值（泥岩普遍含有一定量的有机碳）、 成熟度参数及人为对准多个非烃源岩基线， 这会导致操作复杂、误差较大。 因此， 本文选用胡慧婷等［5］的改进ΔlgR方法， 无需设定有机碳背景值、 成熟度参数及人为对准基线。 因研究区密度测井曲线与实测w（TOC）相关性最好（图2 （d） ）， 故选择密度测井曲线与电阻率测井曲线进行计算。

改进的ΔlgR公式为：

式中：R——实测电阻率值， Ω·m；Rmin——电阻率最小值， Ω·m；K——叠合系数；ρmin——密度最小值， g／cm3；ρ——实测密度值， g／cm3；Rmax——电阻率最大值， Ω·m；ρmax——密度最大值， g／cm3。

最后通过最小二乘法拟合得到公式

式中：w（TOC） ——有机碳的质量分数，%；A，B——系数。

因此通过JFD-1 井、 JFD-5 井的实测w（TOC）数据与电阻率测井、 密度测井曲线数据拟合关系，建立松辽盆地东南隆起区油页岩识别的改进ΔlgR模型， 公式为

改进ΔlgR模型公式的相关系数为0.678 2， 相关性较好。

3.2.2 多元逐步回归模型

多元逐步回归是通过一个一个地输入测井参数， 逐一检验变量显著性， 剔除不合格变量， 保留显著参数， 筛选出与实测w（TOC） 关系密切的测井曲线而建立的预测模型。

以松辽盆地东南隆起区JFD-1 井和JFD-5 井的自然伽马、 电阻率、 声波时差、 密度与实测w（TOC）建立多元逐步回归模型。 首先输入4 条测井参数， 设自然伽马测井参数为X1、 电阻率测井参数为X2、 声波时差测井参数为X3、 密度测井参数为X4， 列出14 种组合方式：Y1=X1，Y2=X2，Y3=X3，Y4=X4，Y5=X21，Y6=X22，Y7=X23，Y8=X24，Y9=X1X2，Y10=X1X3，Y11=X1X4，Y12=X2X3，Y13=X2X4，Y14=X3X4。 以实测w（TOC）为因变量，建立松辽盆地东南隆起区油页岩多元逐步回归模型公式为

多元逐步回归模型公式的相关系数为0.762 9。

通过检验变量显著性、Y4（密度测井参数）和Y13（电阻率测井参数与密度测井参数组合） 为显著参数予以保留， 其余参数为不合格变量予以剔除， 提高了模型的精度。

3.2.3 BP 神经网络模型

BP 神经网络模型由数据流的前向计算（正向传播） 和误差信号的反向传播2 个过程构成［8］，依次经过输入层—隐藏层—输出层。 数据先从输入层进入隐藏层逐层传递， 每层神经元状态仅能影响下一层神经元的状态， 在输出层获得输出， 为正向传播［23-24］。 当输出值与期望值误差大于目标误差时， 网络误差将沿传递来的方向进行反向传播， 使用最速下降法修改神经元的权值减小误差传到输入层再次进行正向传播， 反复这2 个过程直至实际输出与期望输出的误差大小满足要求， 训练结束。

在输入测井数据前应进行数据归一化， 减少不同量纲的测井参数之间差距过大带来的影响［25］。数据归一化公式为

式中：X*——归一化后的计算值；X——实际测井值；Xmax——离散测井数据中的最大值；Xmin——离散测井数据中的最小值。

将松辽盆地东南隆起区JFD-1 井、 JFD-5 井的122 组实测w（TOC） 数据， 按训练集占70%、 测试集占30%进行分配。 输入层为自然伽马、 电阻率、 声波时差、 密度共4 条测井曲线， 并进行数据归一化处理， 隐藏层为6 个神经元， 输出层为预测w（TOC） （图3）。

4 预测结果

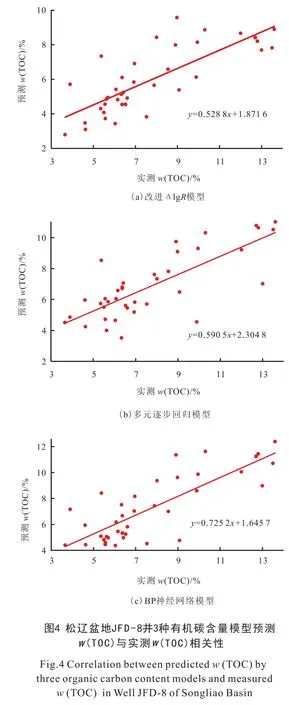
选取松辽盆地东南隆起区上白垩统青山口组JFD-8 井作为预测井， 共有38 个实测w（TOC） 数据。 将JFD-8 井的测井曲线数据输入前文建立的改进ΔlgR模型、 多元逐步回归模型、 BP 神经网络模型， 得到3 种模型的预测w（TOC）， 分析3 种模型的适用条件（图4）。

有机碳含量预测模型的验证包括宏观与微观2方面。

宏观分析可通过对比预测值与实测值相关系数、平均相对误差和平均绝对误差来判断。 相关系数越大、 误差越小， 模型更具适用性。

微观分析是地层中油页岩实测w（TOC） 急剧变化时或变化较小时对模型精度的分析。

本文的微观分析是将松辽盆地东南隆起区上白垩统青山口组JFD-8 井的13 个实测w（TOC）数据划为有机碳含量变化平缓区 （图5 中A 区和B区）， 15 个点划为有机碳含量突变区（图5C 区），对比分析实测w（TOC） 的变化速度与3 种模型预测结果的关系。

4.1 改进ΔlgR 模型

通过电阻率与密度测井曲线叠合建立的改进ΔlgR模型进行JFD-8 井有机碳含量预测， 得到连续的全井段预测w（TOC） 分布， 实测w（TOC）与预测w（TOC） 之间的相关系数、 平均绝对误差、平均相对误差分别为0.782 4、 2.01%、 25.1%（表1）。实测w（TOC） 为3.66%～13.60%， 平均值为7.71%， 改进ΔlgR模型预测w（TOC） 为2.79%～9.58%， 平均值为5.95%， 预测值比实测值范围小， 预测平均值比实测平均值低。

表1 松辽盆地JFD-8 井3 种有机碳含量模型预测w （TOC） 与实测w （TOC） 误差对比Table 1 Comparison of the errors between predicted w（TOC）s by three organic carbon content models and measured w（TOC）s in Well JFD-8 of Songliao Basin

4.2 多元逐步回归模型

以电阻率测井参数、 电阻率测井与密度测井的组合参数为显著参数建立的多元逐步回归模型进行JFD-8 井有机碳含量预测， 得到实测w（TOC） 与预测w（TOC） 之间的相关系数、 平均绝对误差、平均相对误差分别为0.776 8、 1.39%、 17.5%。多元逐步回归模型预测w（TOC） 为3.52% ～11.03%， 平均值是6.86%。 预测值比实测值范围小， 预测平均值比实测平均值低。

4.3 BP 神经网络模型

通过在测井数据与实测w（TOC） 之间建立非线性关系， 在输入层、 隐藏层、 输出层之间反复迭代、 调节权值、 减小误差建立了BP 神经网络模型， 进行JFD-8 井有机碳含量预测， 获得实测w（TOC）与预测w（TOC） 之间的相关系数、 平均绝对误差、 平均相对误差分别为0.806 0、 1.37%、18.8%。 BP 神经网络模型预测w（TOC） 为4.37%～12.39%，平均值为7.24%， 预测值与实测值范围较为接近， 预测平均值与实测平均值较接近。

根据图5 中3 种模型预测效果的对比分析可知， 当油页岩品质较稳定时， 即w（TOC） 平缓区时多元逐步回归模型的预测效果更好， 其次为BP神经网络模型、 改进ΔlgR模型； 对于油页岩品质差异较大时， 即w（TOC）突变区时BP 神经网络模型预测效果最好， 其次为多元逐步回归模型、 改进ΔlgR模型。

5 讨 论

5.1 预测效果

由松辽盆地东南隆起区青山口组油页岩3 种有机碳含量预测模型结果可知， 宏观上BP 神经网络模型相关系数最高、 平均绝对误差最小， 且预测w（TOC）与实测w（TOC） 的取值范围和平均值最为接近； 微观上当油页岩品质较稳定时， 多元逐步回归模型预测效果最好， 其次是BP 神经网络模型、 改进ΔlgR模型， 油页岩品质差异较大时， BP神经网络模型效果最好， 其次为多元逐步回归模型、 改进ΔlgR模型。

5.1.1 改进ΔlgR模型

改进ΔlgR模型虽然相比传统ΔlgR模型操作更方便， 人工造成的误差也减少了， 但效果不及其他2 种模型的主要原因有3 点： （1） 松辽盆地青山口组黄铁矿局部较发育， 对油页岩有机质的测井响应造成干扰， 曲线叠合用的密度测井数据和电阻率测井数据受黄铁矿影响而造成误差； （2） 测井曲线是人为叠合的， 叠合效果不好会造成误差； （3）仅仅2 条曲线难以代表全部地层信息， 因此地质信息的不全面限制了预测的精度。

5.1.2 多元逐步回归模型

多元逐步回归模型整体预测效果优于改进ΔlgR， 且在青山口组油页岩品质发育稳定时， 多元逐步回归预测效果最好， 优于BP 神经网络。 多元逐步回归法通过在多条测井曲线中筛选出对地层有机碳含量值反映明显的曲线建立模型， 剔除了相关性不明显的测井曲线， 达到建立最大相关关系的目的。 由于显著参数的测井曲线与油页岩有机碳含量的相关性强， 当BP 神经网络建模数据量不够时， 多元逐步回归法的预测效果最好。

5.1.3 BP 神经网络模型

BP 神经网络模型整体预测效果最好， 强于多元逐步回归和改进ΔlgR， 且预测w（TOC） 突变区也是效果最好的。 由于青山口组砂泥岩薄层交替出现、 油页岩厚度不一和重矿物富集等， 影响了油页岩的测井响应特征， 常规的线性数学关系无法准确表达有机碳含量与测井数据之间的关系， 利用BP 神经网络模型能够很好地解决此类问题。 BP 神经网络通过隐式非线性方法建立测井信息与有机碳含量之间的联系， 通过多次的数据训练， 改变神经元之间的权值使误差不断下降， 直至小于系统规定误差才可输出， 使预测值更加贴近真实值。 BP 神经网络模型误差主要源于： （1） 训练数据的不充足及神经元选取个数不当引起的过拟合或欠拟合；（2） 区域地质条件的限制。

5.2 方法适用性

综上所述， 根据油页岩有机碳含量突变区与平稳区的趋势对比更能划分出改进ΔlgR模型、 多元逐步回归模型和BP 神经网络模型的各自适用性。

改进ΔlgR模型适用性范围较小且相对最差，当测井曲线与地层中实测w（TOC） 含量拟合相关性较好、 岩性成分较单一、 油页岩呈大段发育且为了操作快速简便时， 该方法较为适用。

多元逐步回归模型同改进ΔlgR模型类似， 受区域地质条件限制因素较大， 即当测井曲线与实测w（TOC）拟合相关性较好时较为适用， 且相关性好的测井曲线越多预测越精确。

改进ΔlgR模型和多元逐步回归模型适用于勘探开发初期井数少、 地化数据不足时。

在勘探开发中后期， 测井资料和地化数据充足时， 面对区域地质情况复杂、 成岩作用、 后期改造作用等因素导致烃源岩的测井响应不明显时［10］BP神经网络模型更具适用性， 尤其是油页岩的w（TOC）突变区。

6 结 论

（1） 松辽盆地东南隆起油页岩在测井上具有高自然伽马、 高电阻率、 高声波时差和低密度的特点。 其中密度与实测w（TOC） 相关性最好， 其次为声波时差和电阻率， 自然伽马相关性相对较差。

（2） 以东南隆起区2 口井的电阻率测井数据与密度测井数据建立改进ΔlgR模型、 以电阻率测井数据和密度测井数据建立多元逐步回归模型、 以测井数据与实测w（TOC）建立BP 神经网络模型。

（3） 通过验证可知， BP 神经网络模型适用于数据量大的地层， 当油页岩层的w（TOC） 变化范围大时更具优越性； 多元逐步回归模型适用于测井曲线对油页岩层段响应好的地层， 显著参数越多预测越精确； 改进ΔlgR模型适用于岩性单一的地层，操作简便， 但误差较大。

（4） 勘探开发初期测井及地化资料不充足时，适用改进ΔlgR模型和多元逐步回归模型； 勘探开发后期测井及地化资料充足时， 适用多元逐步回归模型和BP 神经网络模型。