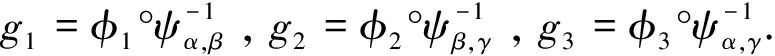A note on Tensor-Matrix based on Einstein product

JIN Xin, XU Jinli

(College of Science, Northeast Forestry University, Harbin 150080, China)

Abstract: The relationship between matrices and tensor based on Einstein product is investigated. All linear isomorphisms between tensor spaces and matrix spaces preserving Einstein product are obtained. The result generalizes transformations given by Brazell et al (equation (2.5) of [1]).

Keywords: mapping problem; Einstein product; multilinear system; matrix

0 Introduction

For tensorsA=(Ai1…ipk1…kq)∈Tm1×…×mp×n1×…×nq(),B=(Bk1…kqj1…jr)∈Tn1×…×nq×l1×…lr(), the Einstein productA*qBof tensor inAandBis a tensor inC∈Tm1×…×mp×l1×…×lr() defined by

An alternative product of two tensorsA∈Tn1×…×nd() of orderd≥2 andB∈Tn1×…×nd() of orderd≥2 is introduced in references [2-3] and various topics such as the inverse, rank, similarity, the modal-k product and congruence under this product can be found in references [4-6]. For a survey of many interesting topics of tensors, including linear maps of tensor products , refer to references [7-9].

Brazell introduced a class of bijective linear transformationsf[1],

f:Tm1×…×mp×n1×…×nq()→M(m1×…×mp)×(n1×…×nq)()

via

(1)

This mapping is also the matrix unfolding of tensors in signal processing applications, e.g., see reference [10]. It is easy to see that

Tm1×…×mp×n1×…×nq()()

Let Γm,nbe all nonsingular linear transfers fromTm1×…×mp×n1×…×nq() toM(m1×…×mp)×(n1×…×nq)()，and the matrix unfoldingfand tensor foldingf-1depend onm1,…,mp,n1,…,nq.

For allA∈Tm1×…×mp×n1×…×nq(),B∈Tn1×…×nq×l1×…lr(), one can check that

f3(A*qBp)=f1(A)·f2(B)

(2)

wheref1,f2,f3are defined in (1), and·refers to the usual matrix multiplication. In recent years, results of tensor via Einstein product such as multilinear SVD[1], generalized inverse[11]are studied by (1) and (2). A natural question is what are all possible forms of bijective linear transformations satisfying (2).

In this note, we answer this question. For clarity, let

α:[m1]×…×[mp]→[m1×…×mp]
β:[n1]×…×[nq]→[n1×…×nq]
γ:[l1]×…×[lr]→[l1×…×lr]

be bijective maps for allm,n,lwhich are integers greater than or equal to 2. We defineψα,β∈Γm,nby

ψα,β(εi1…ipk1…kq)=Eα(i1…ip),β(k1…kq)

(3)

whereεi1…ipk1…kqis of 1 in (i1…ipk1…kq)-th entry and 0 otherwise andEα(i1…ip),β(k1…kq)is of 1 in (α(i1…ip),β(k1…kq))-th entry and 0 otherwise. Similarly, we can defineψβ,γ∈Γn,landψα,γ=Γm,l.Our main result is:

Theorem1(Main Theorem) Letφ1∈Γm,n,φ2∈Γn,l,φ3∈Γm,l.If

φ3(A*qB)=φ1(A)φ2(B)

for allA∈Tm1×…×mp×n1×…×nq(),B∈Tn1×…×nq×l1×…×lr(), then there exist bijective maps

α:[m1]×…×[mp]→[m1×…×mp],β:[n1]×…×[nq]→[n1×…×nq],γ:[l1]×…×[lr]→[l1×…×lr] and invertible matricesP∈Mm×m(),R∈Mn×n(),Q∈Ml×l()such that

φ1(A)=Pψα,β(A)R

φ2(B)=R-1ψβ,γ(B)Q

φ3(C)=Pψα,γ(C)Q

for allA∈Tm1×…×mp×n1×…×nq(),B∈Tn1×…×nq×l1×…×lr(),C∈Tm1×…×mp×l1×…×lr().

1 The proof of main result

Lemma1Letψα,β,ψρ,γbe defined as (3) andφ3∈Γm,l. If

φ3(A*qB)=ψα,β(A)ψρ,γ(B)

for allA∈Tm1×…×mp×n1×…×nq(),B∈Tn1×…×nq×l1×…×lr(), thenβ=ρandφ3=ψα,γ.

ProofSuppose (i1…ip)∈[m1]×…×[mp],(j1…jr)∈[l1]×…×[lr]and(k1…kq)∈[n1]×…×[nq]. Sinceφ3is bijective, we obtain

0≠φ3(εi1…ipj1…jr)=φ3(εi1…ipk1…kq*qεk1…kqj1…jr)

=ψα,β(εi1…ipk1…kq)ψρ,γ(εk1…kqj1…jr)

=Eα(i1…ip),β(k1…kq)Eρ(k1…kq),γ(j1…jr)

=δβ(k1…kq),ρ(k1…kq)Eα(i1…ip),γ(j1…jr)

Thusβ(k1…kq)=ρ(k1…kq) for all (k1…kq)∈[n1]×…×[nq], that isβ=ρand

φ3(εi1…ipj1…jr)=Eα(i1…ip),γ(j1…jr)=ψα,γ(εi1…ipj1…jr)

Hence,φ3=ψα,γ.

Conclusion1Letψα,β,ψβ,γandψα,γbe defined as (3), then

for allA∈Mm×n(),B∈Mn×l().

ProofThe conclusion follows from

Lemma2(Theorem 3.3 of reference [12]) Supposeφ:Mm×n()→Mm×n() is a linear transformation such that

rankφ(A)=k⟺rank(A)=k

wherek≤min{m,n}. Then there exist invertible matricesP∈Mm×m(),R∈Mn×n() such that

φ(A)=PAR,∀A∈Mm×n()

orm=n≥2

φ(A)=PATR,∀A∈Mm×n()

Lemma3Supposeg1,g2,g3are bijective linear transformations onMm×n(),Mn×l(),Mm×l(), respectively. If

g3(AB)=g1(A)g2(B)

for allA∈Mm×n(),B∈Mn×l(),C∈Mm×l(). Then there exist invertible matricesP∈Mm×m(),R∈Mn×n(),Q∈Ml×l() such that

g1(A)=PAR,∀A∈Mm×n()

g2(B)=R-1BQ,∀B∈Mn×l()

g3(C)=PCQ,∀C∈Mm×l()

ProofFirstly, we prove thatg1preserves maximal rank onMm×n() in both directions.

Case 1:m≤n. We chooseA∈Mm×n() with rank(A)=m, Then

{AB:B∈Mn×l()}=Mm×l()

Sinceg3is bijective,g3(AB)=g1(A)g2(B) can run over all the matrices inMm×l(). Thus, rank(g1(A))=m. Contrarily, if rank(g1(A))=m, theng1(A)g2(B)=g3(AB) can be an arbitrary matrix inMm×l(). Due to the bijectivty ofg3,ABcan be an arbitrary matrix inMm×l(), and hence, rank(A)=m.

Case 2:m>n. We chooseAwith rank(A)=nand suppose rank(g1(A))≠n. Then there existsX1≠X2∈Mn×l() such that

g1(A)X1=g1(A)X2

Sinceg2is bijective, we obtainB1≠B2∈Mn×l() such thatg2(Bi)=Xi,i=1,2.It follows from

g3(AB1)=g1(A)g2(B1)=g1(A)X1=g1(A)g2(B2)=g3(AB2)

and the bijectivity ofg3thatAB1=AB2. By the assumption of rank(A)=n, we can getB1=B2, a contradiction. Contrarily, if rank(g1(A))=nand rank(A)

g1(A)g2(B1)=g3(AB1)=g3(AB2)=g1(A)g2(B2)

Note that rank(g1(A))=n, henceg2(B1)=g2(B2). Sinceg2is bijective,B1=B2is contradictory.

By Lemma 2, there exist invertible matricesP∈Mm×m() andR∈Mn×n() such that

g1(A)=PAR, ∀A∈Mm×n()

(4)

orm=n≥2

g1(A)=PATR, ∀A∈Mm×n()

(5)

Similarly, we can prove thatgpreserves maximal rank onMn×l() in both directions, and hence , there exist invertible matricesS∈Mn×n(),Q∈Ml×l() such that

g2(B)=SBQ, ∀B∈Mn×l()

(6)

orn=l≥2

g2(B)=SBTQ, ∀B∈Mn×l()

(7)

We next prove that (4) and (6) are the only cases, others will not happen.

If (5) and (6) hold, letA=Eii,B=Ej1,i,j∈[n],RS=U=(uij)n×n. It follows from

δijg3(Ei1)=g3(EiiEj1)=PEiiUEj1Q=uijPEi1Q

thatuij=0,∀i≠j. SetA=E12,B=E21, then

0≠g3(E11)=PE21diag(u11,…,unn)E21Q=0

which is a contradiction.

If (4) and (7) hold, letA=E1i,B=Ejj,i,j∈[n],RS=U=(uij)n×n. It follows from

δijg3(E1j)=g3(E1iEjj)=PE1iUEjjQ=uijPE1jQ

thatuij=0,∀i≠j. SetA=E12,B=E21, then

0≠g3(E11)=PE12diag(u11,…,unn)E12Q=0

Similarly, one can prove that (5), (7) will not happen.

Next , we assume that (4), (6) hold. LetRS=U=(uij)n×n. TakingA=E1i,B=Ej1,i,j∈[n], we obtain

δijg3(E11)=g3(E1iEj1)=PE1iUEj1Q=uijPE11Q

Hence

uij=0,∀i≠j

and

ujj=u11,∀j∈[n]

Therefore we haveRS=λI, for someλ≠0. ReplaceQbyλ-1Q, It follows from (4) and (6) that

g1(A)=PAR, ∀A∈Mm×n()

and

g2(B)=R-1BQ, ∀B∈Mn×l()

Hence

g3(Eij)=g3(Ei1E1j)=PEijQ, ∀i∈[m],j∈[l]

We get

g3(C)=PCQ, ∀C∈Mm×l()

for anyA∈Mm×n(),B∈Mn×l().

By Lemma 3, there exist invertible matricesP∈Mm×m(),R∈Mn×n(),Q∈Ml×l() such that

g1(A)=PAR,∀A∈Mm×n()

g2(B)=R-1BQ,∀B∈Mn×l()

g3(C)=PCQ,∀C∈Mm×l()

and the theorem follows.

Domestic studies on linear preserving problem began in 1989[13], for more research on preserving problem and tensor refer to references [14-17] and their references.