基于能量的多模态推覆分析方法在桥梁高墩抗震分析中的应用

周 迅 唐耀明 李建中，* 徐艳珊

（1.同济大学桥梁工程系，上海 200092；2.云南功东高速公路建设指挥部，昆明 650000）

0 引言

近年来，随着经济的飞速发展，我国西南地区建立了大量桥梁。由于西南地区高山峡谷众多，超过40%的桥梁结构墩高大于40 m，部分墩高超过了100 m。而西南地区地震频发，2008 年汶川地震里氏震级达8.0 级、2013 年雅安地震里氏震级达7.0 级［1］。桥梁结构作为交通网络中的重要节点，在地震发生后仍应当具有一定的通行能力以充当生命线的角色。我国桥梁抗震设计规范要求对于墩高超过40 m、墩身在计算方向第一阶振型参与质量系数小于60%且结构进入塑性的高墩桥梁应作专项研究。因此，需要对桥梁高墩合理的抗震设计方法进行研究。

目前常用的地震反应计算分析方法中，非线性时程分析方法（NLTHA）作为一种通用方法，可以有效地评估结构的地震需求及能力。但在实际应用中，NLTHA 方法面临了一些问题［2］，如：地震具有随机性，若计算时输入的地震时程数量较少，计算得到的结果具有局限性；计算结果对参数变化敏感，如Rayleigh 阻尼合理取值对地震响应影响较大；计算过程复杂。

随着基于性能的抗震设计方法的提出和发展，一些学者提出了非线性静力方法（推覆分析Pushover），非线性静力方法被ATC-40、FEMA-273等规范广泛采用［2］。早期推覆分析方法采用了固定的侧向加载模式，假定结构在地震中主要受一阶振型控制，而忽略高阶振型的影响；将单调增加的侧向荷载分布加载于结构上，以此来估计结构地震响应。

研究表明［3］，传统的推覆分析方法主要适用于一阶振型起主要贡献的结构。对于中、低桥墩，由于其桥墩本身质量和高阶振型贡献可以忽略，采用推覆分析方法是可行的。对于高墩，由于其具有截面尺寸大、结构周期长、墩身质量大等特点，计算时需要考虑墩身质量以及高阶振型的影响［1］。

针对高阶振型贡献这一问题，A.K.Chopra 与R.K.Goel［3］提出了基于多模态的推覆分析方法（MPA），并验证了该方法的广泛适用性［4-5］。ENRIQUE HERNÁNDEZ-MONTES 等［6］针对MPA方法中可能遇到的结构顶端位移“折返”问题［7］，提出了基于能量的多模态推覆分析，即从能量的角度得到各阶振型对应单自由度体系的Dn关系。

本文首先对MPA 方法进行了简要的回顾；其次，对基于能量的模态推覆分析（Energy-based Modal Pushover Analysis，EMPA）进行介绍；后将EMPA 方法应用于90 m 高墩抗震性能评估，与非线性时程分析（NLTHA）结果对比，以研究其适用性，并对合理的模态组合方法提出了建议；最后讨论不同高度桥墩采用EMPA 方法进行估计时，应采用的合理模态数量。

1 EMPA方法及其在高墩中的应用

1.1 EMPA方法介绍

自A.K.Chopra 与R.K.Goel［3］于2002 年提出多模态推覆分析方法（MPA）后，该方法在房屋建筑结构的抗震设计中得到广泛应用。对结构性能需求进行估计时，MPA 方法采用多模态的侧向加载模式［3］，即对结构水平加载对应于各阶振型的侧向力

式中：为第n阶侧向加载模式；m为结构总质量矩阵；ϕn为第n阶振型向量。

将加载于各节点，并考虑结构的非线性特性，得到结构底部剪力Vbn-顶端位移urn的关系，如图1所示。

图1 第n阶模态推覆分析的Vbn-urn关系Fig.1 Relationship between Vbn and urn from nth-mode pushover analysis

MPA 方法假定结构进入非线性后，各阶振型间耦合效应对总响应的贡献较小［3］，因而沿用振型分解的方法，得到第n阶模态振动方程，如式（2）所示：

其中，ωn、ξn为第n阶模态的频率及阻尼比；Dn、Ln、Fsn/Ln分别由式（3）—式（5）计算得到。

式中：ι为元素全为1 的列向量；ϕrn为第n阶振型顶端节点对应的振型坐标；Γn为第n阶振型的振型参与系数，可由式（6）计算得到。

通过式（3）、式（5），则可由第n阶振型的Vbnurn关系得到关系如图2所示。

图2 第n阶模态推覆分析的FsnLn-Dn关系及多线性等效Fig.2 Relationship between FsnLn and Dn from nth-mode pushover analysis and its idealization

通过求解以上非线性单自由度振动方程求出Dn(t)，并由式（7）估计结构地震反应。

求解得到各阶振型峰值响应后，A.K.Chopra与R.K.Goel［3］的研究表明，可以采用适用于线性结构的振型组合求解结构的峰值响应。相比于传统的推覆分析方法，MPA 方法考虑多阶振型对结构整体振动的贡献，特别对于受高阶振型控制明显的高耸结构、柔性结构有良好的适用性，较好地解决了考虑高阶振型效应的侧向加载模式问题。

但采用MPA 方法时，在对结构施加高阶振型的侧向力进行推倒分析时，会出现顶端位移减小甚至变为负的情况，即可能遇到如图3 所示的“折返”问题［8］，得到的关系是不符合基本的力学概念，且违反热力学定律的。究其原因，结构进入塑性后，MPA 方法沿用了结构弹性阶段的侧向加载模式。在第2 阶推覆过程中，结构顶端位移的“折返”导致了FsnLn-Dn出现“折返”。

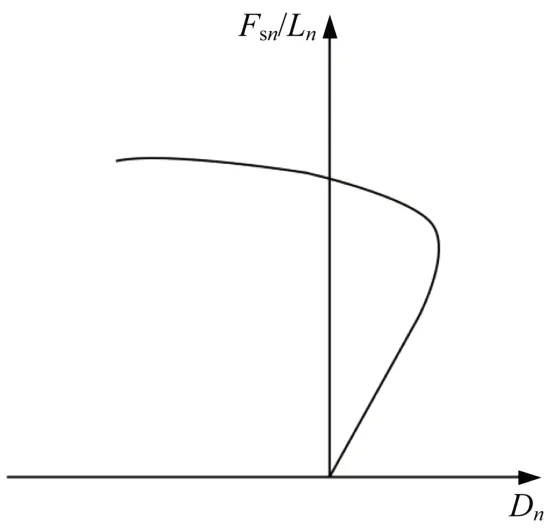
图3 模态推覆分析FsnLn-Dn曲线“折返”现象Fig.3 Reversal ofFsnLn-Dn curve encountered in MPA

针对这一问题，ENRIQUE HERNÁNDEZMONTES 等提出了基于能量的多模态推覆分析［6］，即从能量的角度得到某一阶振型对应单自由度体系的FsnLn-Dn关系。结构处于弹性阶段时，侧向荷载输入结构的能量瞬时值E为

式中：fTs为恢复力向量；u为节点位移向量。对处于弹性阶段的结构，有

式中，k为结构的总刚度矩阵。

由振型的正交性，对应于每一阶振型的恢复力向量fsn仅在这一振型的位移un上做功。则弹性阶段，第n阶中输入结构的能量瞬时值En为

基底剪力Vbn则为结构受到的侧向力之和，即

综合式（10）、式（11），如已知输入能量En及基底剪力Vbn，则可求得Dn

结构进入塑性后，则应采用增量形式得到输入结构的能量瞬时值ΔEn

则ΔDn为

同时式（15）的关系依然存在。

图4 EMPA方法中Vbn-Dn的建立Fig.4 Vbn-Dn curve obtained from EMPA

相比于MPA 方法，EMPA 方法从能量的角度直接建立基底剪力Vbn和广义位移Dn之间的关系，从而由式（15）得到FsnLn-Dn关系。而非从结构顶端节点位移的角度，由式（3）得到广义位移Dn，避免了FsnLn-Dn出现“折返”的现象。

但是，EMPA 方法依然采用了=mϕn的加载模式，并在加载过程中保持不变。因此采用EMPA 方法对FsnLn-Dn关系修正，仅仅是对MPA方法的适用范围进行了推广。

下面给出EMPA方法的简要步骤：

（1）计算初始处于弹性状态的结构自振频率ωn及振型ϕn。

（2）将每一阶振型对应的侧向加载模式s＊n=mϕn施加于结构，直到节点位移达到事先规定的值（常常需要迭代求解），并记录结构节点位移u及底部剪力Vbn，一般计算2至3阶。

（3）计算结构节点位移增量，由式（13）计算得到侧向力所做的功增量ΔEn。

（4）由式（14）计算ΔDn并累加得到Dn，由此得到Vbn-Dn关系。

（5）由式（15）得到FsnLn-Dn关系，并用多段线性函数拟合。

（6）对第n阶模态的振动方程式（2）进行求解，求出Dn(t)。

（7）由式（7）估计结构地震反应或通过振型组合方法得到峰值。

1.2 算例及验证

1.2.1 背景工程

本文以我国西南地区某等跨度等墩高连续梁桥为例，在建模时将高墩桥梁模型简化为等截面单墩模型。单墩计算模型采用墩底固结的悬臂直梁，墩身质量集中于相应的节点，将与桥墩相邻跨度为L的上部结构质量等效为墩顶的集中质量如图5（a）所示，质量仅考虑平动。其中，桥墩高度H为90 m，墩身质量mi为301.1 t，墩顶附加质量M为3 150.6 t；桥墩等效截面尺寸B取9.4 m，壁厚t为1.2 m。

图5 桥墩计算原型Fig.5 Prototype of the bridge

1.2.2 计算模型

有限元计算采用OpenSees 软件；桥墩采用基于柔度法的纤维单元进行模拟，并考虑到编程的一致性，沿高度方向共分为30 个单元。其中钢筋纤维采用双线性本构如图6（a），初始弹性模量取为206 GPa，钢筋屈服强度取为400 MPa，屈服后模量与初始弹性模量之比α取0.001。保护层及核心混凝土纤维采用Kent-Scott-Park 本构如图6（b），不考虑混凝土的抗拉强度，其中保护层混凝土抗压强度取26.8 MPa，核心混凝土抗压强度取为28.5 MPa［9］。

图6 计算模型中所采用的本构关系Fig.6 Constitutive relationship in the numerical model

从美国太平洋地震工程中心的强震数据库中选取选用了7条地震波，各地震波记录见表1。同时对每条地震波进行峰值调整，分别调整至0.2g、0.4g、0.6g、0.8g。

表1 地震动参数Table 1 Selected ground motion records

1.3 计算结果及分析

由特征值分析得到90 m 高墩前三阶周期及振型参与质量系数如表2 所示；前三阶模态信息ϕn及侧向力分布s*n，如图7所示。

图7 90 m高墩前三阶模态推覆信息Fig.7 Pushover information of the first three modes of the 90 m high pier

表2 90 m桥墩前三阶周期及振型参与质量系数Table 2 First three periods of the 90 m high pier and the participating mass ratios respectively

图8 给出了由EMPA 方法获得的FsnLn-Dn与MPA方法的对比。

由图8 可以看出，EMPA 方法解决了第二阶FsnLn-Dn曲线的“折返”问题。对于第一阶推覆分析，EMPA与MPA方法结果相同。

图8 由EMPA方法获得的FsnLn-Dn与MPA方法结果的对比Fig.8 Comparison between theFsnLn-Dn curves from MPA and EMPA

非线性时程分析方法（NLTHA）作为一种通用方法，可以有效地评估结构的地震需求及能力；这里将NLTHA 方法得到的结果作为参照。图9至图12给出EQ1地震作用下，EMPA与NLTHA方法获得结构需求的对比，其中EMPA 方法获得各阶振型下峰值后，再通过SRSS方法组合得到结构需求的峰值。同时，给出桥墩截面屈服曲率3.4×10-4m-1作为参考。

由图9 至图12 可以看出，EMPA 方法较好地估计了高墩墩身的节点位移峰值，但对墩身截面曲率峰值及剪力峰值的估计，特别是结构进入非线性（截面曲率达到3.4×10-4m-1）后的估计存在较大误差。若要将EMPA 方法运用于高墩抗震性能评估，需要对方法进行一定的修正。

图9 EQ1峰值加速度调整为0.2g时采用EMPA与NLTHA方法获得的结构需求Fig.9 Structural demand from EMPA and NLTHA for EQ1 with PGA adjusted to 0.2g

图10 EQ1峰值加速度调整为0.4g时采用EMPA与NLTHA方法获得的结构需求Fig.10 Structural demand from EMPA and NLTHA for EQ1 with PGA adjusted to 0.4g

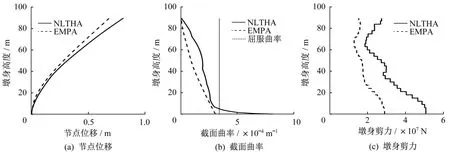
图11 EQ1峰值加速度调整为0.6g时采用EMPA与NLTHA方法获得的结构需求Fig.11 Structural demand from EMPA and NLTHA for EQ1 with PGA adjusted to 0.6g

图12 EQ1峰值加速度调整为0.8g时采用EMPA与NLTHA方法获得的结构需求Fig.12 Structural demand from EMPA and NLTHA for EQ1 with PGA adjusted to 0.8g

2 组合方法讨论

EMPA 方法从能量的角度直接获得FsnLn-Dn关系，而非通过某一节点的位移获得，因此能够避免FsnLn-Dn曲线的“折返”现象。但EMPA方法终究还是通过对结构施加侧向力分布=mϕn。因此MPA方法的误差，EMPA方法均继承［3］：

（1）采用不变的侧向力分布，不能体现结构屈服后惯性力的重分布现象；

（2）忽略了结构屈服后各阶振型的耦合作用；

（3）使用静力方法不能反映结构在动力作用下的能量的传递；

（4）采用振型组合方法引起的误差。

其中，误差4 中所采用的振型组合方法如SRSS，均是基于线弹性经典阻尼系统和结构响应为零均值平稳高斯过程得到的。将SRSS 方法引入非线性静力方法中会带来一定的误差。为改进MPA 方法中振型组合所带来的误差，A.S.Moghadam［10］提出采用振型参与系数对各阶推覆分析结果进行加权求和，但这一方法降低了高阶振型对结构的影响。本文仅研究常见的组合方法［11］，包括SRSS 方法、CQC 方法、绝对值求和（Abs）方法的有效性。由于桥墩结构各阶频率相差较大，可近似地认为SRSS 方法与CQC 方法结果相同，这里仅给出SRSS方法的结果。采用以上组合方法计算出90 m 高墩节点位移、截面曲率及墩身剪力峰值响应与NLTHA方法间的相对误差，并对7 条地震波下的误差取平均，绘于图13 至图16中。

图13 七条地震波峰值加速度调整为0.2g时结构需求的相对误差平均值Fig.13 Average relative error of structural demand for 7 waves with PGA adjusted to 0.2g

图14 七条地震波峰值加速度调整为0.4g时结构需求的相对误差平均值Fig.14 Average relative error of structural demand for 7 waves with PGA adjusted to 0.4g

图15 七条地震波峰值加速度调整为0.6g时结构需求的相对误差平均值Fig.15 Average relative error of structural demand for 7 waves with PGA adjusted to 0.6g

图16 七条地震波峰值加速度调整为0.8g时结构需求的相对误差平均值Fig.16 Average relative error of structural demand for 7 waves with PGA adjusted to 0.8g

由图13 至图16 可见，采用绝对值求和方法（Abs）进行进行振型组合，在一定程度上补偿了由于忽略结构进入塑性后振型耦合所带来的误差；其结果大于SRSS 方法，提高了桥墩结构进入塑性后的节点位移及墩身剪力计算精度。对于在地震中处于弹性阶段的结构，可以近似视为线弹性经典阻尼系统，结构响应可以近似为零均值平稳高斯过程，如本例中地震波峰值加速度调整为0.2g 下的桥墩结构，采用Abs 方法对精度的提高不明显，如图13所示。

在估计截面曲率时采用绝对值求和方法与SRSS 方法计算精度相近。其中，两者大部分情况下低估了距墩顶0～15 m 处截面曲率，相对误差超过了50%，但这些部位截面曲率较小（由图9 至图12 可以得出这样的结论），因此并不控制桥墩的抗震设计。

3 墩高效应

为了进一步讨论EMPA 计算高墩地震响应的有效性，分别建立高度为30 m、60 m、90 m 的桥墩有限元模型，各桥墩的主要参数以及一阶振型参与质量系数如表3所示。

表3 不同高度桥墩的基本参数Table 3 Features of piers of different heights

采用EMPA 方法，针对不同墩高，计算得到七条地震波（峰值加速度调整为0.6g）下，前3 阶响应各自对总响应贡献率的均值如图17 至图19 所示，在进行振型组合时采用Abs组合。

由图17 至图19 可以看出：随着墩高增加，高阶振型响应的贡献明显增大；相比于节点位移，高阶振型对截面曲率与墩身剪力的贡献更显著。实际上，当结构处于弹性阶段时，EMPA 方法与反应谱方法是等效的，高阶振型的贡献对位移（谱位移的变化）的影响将小于其对力（谱加速度的变化）的影响，如图20所示。

图17 七条地震波峰值加速度调整为0.6g时30 m桥墩各阶推覆分析结果对组合值的贡献率平均值Fig.17 Average modal contribution rate of 30 m pier for 7 waves with PGA adjusted to 0.6g

图18 七条地震波峰值加速度调整为0.6g时60 m桥墩各阶推覆分析结果对组合值的贡献率平均值Fig.18 Average modal contribution rate of 60 m pier for 7 waves with PGA adjusted to 0.6g

图19 七条地震波峰值加速度调整为0.6g时90 m桥墩各阶推覆分析结果对组合值的贡献率平均值Fig.19 Average modal contribution rate of 90 m pier for 7 waves with PGA adjusted to 0.6g

图20 结构周期变化带来谱位移、谱加速度的增减Fig.20 Fluctuations of spectral displacement and spectral acceleration initiated by variations of periods

为进一步研究不同墩高下EMPA 方法合理的分析阶数，定义综合贡献率Ai为

式中：i为推覆分析的阶数；ci为前i阶分析得到沿高度变化的结果；∆h为求和区间长度。

显然，A3=100%。针对不同墩高下各结构需求，前i阶结果的综合贡献率Ai如表4—表6所示。

表4 不同墩高下前i阶结果对节点位移的综合贡献率Table 4 Comprehensive contribution rate of nodal displacement for piers of different heights

表5 不同墩高下前i阶结果对截面曲率的综合贡献率Table 5 Comprehensive contribution rate of curvature for piers of different heights

表6 不同墩高下前i阶结果对墩身剪力的综合贡献率Table 6 Comprehensive contribution rate of shear force for piers of different heights

其中，对于高度为30 m 的桥墩，其墩身节点位移由第1 阶响应控制，而截面曲率及墩身剪力由前2 阶响应控制。对于高度为60 m 的桥墩，位移、曲率和剪力由前2 阶响应控制，第2 阶的贡献明显增加。对于高度为90 m 的桥墩，除位移外前三阶响应的贡献均不能忽略，高阶振型的贡献进一步增大。在EMPA 计算中，随着桥墩高度的增大，应采用更多阶数的响应结果进行组合以获得正确的结果。

4 结论

本文首先对基于能量的模态推覆分析进行介绍；后研究其针对桥梁高墩抗震性能评估的适用性，并与非线性时程分析结果对比，研究合理的模态组合方法；最后对不同性能指标、不同高度桥墩应采用的EMPA阶数。并得到以下结论：

（1）传统的MPA 方法中会出现FsnLn-Dn曲线“折返”的现象，因此不能很好地适应所有结构类型，基于能量的模态推覆分析可以解决这一问题。

（2）将EMPA 方法应用于桥梁高墩，可以较好地估计墩身的节点位移峰值，但对墩身截面曲率峰值及剪力峰值的估计，特别是结构进入非线性后的估计存在较大误差；相比于常用的SRSS方法，结构进入非线性后采用绝对值求和（Abs）的模态组合方法计算简便，并能保证良好的精度。

（3）随着墩高的增加，高阶振型的贡献明显。在计算中应采用更多阶数的响应结果进行组合以获得正确的结果。计算节点位移时，取第1 阶EMPA 结果已经能够保证一定的精度；而计算截面曲率或墩身剪力时，应取前3 阶的EMPA 结果进行组合。