装配式可伸缩钢结构看台力学性能分析及现场监测

贾 斌 张 敏 魏明宇 李鹏程

（1.四川省建筑科学研究院有限公司，成都 610081；2.重庆大学土木工程学院，重庆 400045；3.中国五冶集团有限公司，成都 200120）

0 引言

临时看台结构在近年各大型体育赛事及社会活动中应用广泛，获得了良好的社会及经济效益。可伸缩钢结构看台采用装配式活动架体作为支撑结构，具有不受场地限制、安装方便、易于拆卸等特点，通过机械传动装置可以轻松完成看台结构的展开与折叠，适合大空间建筑室内使用。国外对于此类临时看台结构进行了诸多研究工作［1-2］，并制定了相关设计规范［3］。本文以某大型装配式可伸缩钢结构看台为研究对象，考虑结构体系特点、边界约束条件及节点构造形式建立整体有限元分析模型，讨论最不利荷载下的结构内力分布规律。由于该装配式可伸缩看台结构构造特点及柱脚约束与传统钢结构看台差异较大，采用线性屈曲分析方法及考虑几何非线性和材料非线性影响的极限承载力分析方法对看台结构的整体稳定性能进行比较。基于使用过程中现场应力及变形监测数据，对该看台活荷载动力系数提出建议值。

1 工程概况

某可伸缩装配式钢结构看台在完全展开状态下共计有29 阶1 400 座，结构横向宽28.5 m、纵向长26.6 m，最后一排结构高度约8 m。钢结构自重约82吨，满座后重量达到180吨，看台钢结构由矩形钢管立柱、卷边C型钢横梁、方钢管次梁及立柱底部锁脚梁组成，立柱间采用扁钢条作为柔性支撑系统。为满足可折叠需求，看台立柱底部共设置1 836个由聚氨酯材料制造的触地脚轮，由驱动电机带动72 个驱动轮完成钢结构看台的展开与折叠，图1 为结构展开状态与折叠状态。该看台完全展开时的投影面积为742 m2，处于折叠状态时的投影面积为140 m2，约80%的看台空间可被释放。当其完全展开时，通过立柱顶部及底部双重钩锁设计，使看台钢结构由活动机构状态转变为固定结构状态。

图1 结构展开及折叠状态（单位：mm）Fig.1 Expanded and folding state of structure（Unit：mm）

2 结构建模及荷载工况

2.1 边界条件与荷载工况

该可伸缩看台结构沿轴向设置了三处刚度较大的不可折叠区，以此可区分为高中低三个高度区域，沿结构宽度方向因使用功能及结构构造特点可划分为结构构造相同的6 个看台单元。看台完全展开并且锁扣就位后的结构体系可简化为梁柱铰接的排架结构，沿横向设置柔性拉杆以增加侧向刚度。按照图2 所示结构功能分区，考虑结构对称性及荷载对称性，选择1 个看台单元进行建模分析。本项目中结构所采用的钢材均为Q235B 材料，弹性模量为206 GPa，泊松比为0.3，密度为7 850 kg/m3。立柱采用矩形钢管、卷边C型钢作为主横梁、方钢管作为座位下次梁及立柱底部锁脚梁，具体规格参数见表1。

图2 看台结构功能分区Fig.2 Structural partition of the grandstand

表1 构件规格参数Table 1 Member specifications of the grandstand

采用通用有限元软件建立图3 所示1 个看台单元分析模型。钢材采用双线性随动强化模型，假定不考虑屈服后强化系数为理想弹塑性。看台结构底部由聚氨酯材料制造的触地脚轮支承于室内地面，当柱脚锁闭装置启动后，柱脚能够有效约束平动，但约束转动的能力较弱，因此偏于安全地采用铰接支座模拟结构底部边界条件。所有梁柱单元均采用梁单元模拟，根据实际情况释放相应位置转动自由度。柱间拉杆采用只受拉杆单元模拟，不考虑其承压能力。有限元模型所采用材料及构件规格均与实际结构相同，并且考虑梁柱连接构造产生的偏心影响，有限元分析模型如图3所示。

图3 结构有限元模型Fig.3 Finite element model of structure

2.2 荷载工况布置

看台结构主要承受上部看台设备恒荷载及人群活荷载，依据甲方需求并结合《演出场所安全技术要求》（WH/T 42—2011）［4］确定恒载设计值为0.5 kN/m2，人群活荷载设计值为3.5 kN/m2。观众在看台上产生的人群活载非常复杂，且往往是造成此类结构倒塌的主要原因，人群活载对轻质、柔性看台影响极为不利。活荷载考虑1.2 的动力放大系数后取4.2 kN/m2，同时考虑人群在水平向产生的水平活荷载，其值取竖向活荷载的1/10。由于看台处于室内且为临时性结构，因此不考虑风荷载及地震荷载。

共计考虑6 种工况及其18 种组合（表2），其中D表示恒荷载、L1表示满布竖向活荷载、L2表示沿看台轴向向前水平活载、L3表示沿看台轴向向后水平活载、L4表示沿看台横向水平活载、L5表示沿看台轴向间隔布置竖向活载、L6表示沿看台横向间隔布置竖向活载。

表2 荷载工况组合Table 2 Load case combinations

2.3 分析验算结果

各工况下最不利内力见表3。对于立柱而言，最不利工况组合为LS1、LS2 及LS11，其轴力最小工况组合为LS7～LS9 以及LS14，沿看台轴向水平荷载对结构立柱轴力影响非常明显，横向水平荷载主要由柱间支撑抵抗，因此立柱轴力较小。前11 个工况中薄壁C 型钢主梁的内力较为接近，表明其内力主要受恒载及竖向活荷载控制。考虑活荷载不匀均布置的LS8 及LS9 工况组合计算结果表明，立柱轴力及主梁内力均较小，结构体系构成特点对非均布荷载作用并不敏感。

表3 结构最不利内力Table 3 Most unfavorable inner force

次梁在各工况组合下的弯矩差别不大，在沿看台轴向水平力作用下，其轴力增大较为明显。侧向荷载仅为人群活荷载引起的水平荷载，因此柱间柔性支撑轴力较小，当沿看台横向水平活载参与组合时其内力相对较大。立柱构件强度应力比最大值为0.86，稳定应力比最大值为0.88。薄壁C 型钢主梁构件的强度应力比最大值为0.83，稳定应力比最大值为0.89，以上结构主构件应力比满足规范要求。

3 整体稳定性分析

鉴于本文看台结构与传统意义上的钢结构看台存在一定设计构造上的差别，常规计算分析不一定能准确找出结构构件薄弱部位，因此采用线性及非线性屈曲分析方法对看台结构整体稳定性能进行评价。《钢结构设计规范》（GB 50017）对钢结构的整体稳定性没有明确规定，只是从构件层次提出考虑二阶效应的设计方法［5］。为了能够对其整体稳定分析结果进行分析判断，参考《空间网格结构技术规程》（JGJ 7）中关于整体稳定性分析的相关方法［6］。结构整体稳定判断准则可采用如下方法：①荷载-位移曲线判定准则，即当结构荷载-位移曲线达到其顶点时认为进入临界状态；②承荷极限判定准则，即当结构以缓慢的输电比例加载，达到最大值时即认为此为稳定临界状态；③荷载-位移曲线斜率判定准则，即当曲线斜率为零时达到稳定临界状态。

3.1 线性屈曲分析

屈曲分析主要用于确定结构失稳前的极值荷载和屈曲模态，采用线性特征值屈曲分析与非线性屈曲分析方法进行研究。线性特征值屈曲分析用于预测一个理想弹性结构的理论屈曲荷载，并给出结构稳定承载力的上限，同时特征值屈曲分析中获得的屈曲模态也可以给非线性屈曲分析提供初始缺陷。计算采用基本荷载组合LS7。

提取本文活动看台结构前四阶屈曲模态如图4 所示，从前四阶屈曲模态可以看出，一阶模态变形表现为结构整体横向侧移，并存在一定扭转变形；二阶模态为高区第二排立柱侧向局部失稳；三阶模态为高区第三排立柱侧向局部失稳；四阶模态为高区第四排立柱侧向局部失稳。计算表明，结构前四阶屈曲临界荷载分别为8.1 kN、9.6 kN、10.4 kN 和11.1 kN，将第一阶整体屈曲模态作为初始缺陷引入后面非线性屈曲分析中，初始几何缺陷考虑为柱高的1/300。

图4 前四阶屈曲模态Fig.4 The first four buckling modes

3.2 非线性屈曲分析

本文以看台结构发生最大X向及Z向变形处作为参考点，按照荷载-位移曲线判断准则，计算迭代不收敛时刻为稳定临界状态。图5 分别列出了基于两种工况组合的非线性屈曲分析所得荷载-位移曲线，随着荷载水平增大，由于几何非线性及材料非线性的发展，结构刚度不断降低。初始阶段荷载-位移曲线斜率较大，当荷载达到一定程度之后，结构非线性程度不断加深，曲线斜率急剧减小，表明结构整体刚度显著降低，最终计算收敛困难。荷载位移曲线表明：极限承载力作用下结构X方向最大变形为54 mm（LS4）和101 mm（LS5）；极限荷载作用下结构Z方向最大变形为19 mm（LS4）和100 mm（LS5）。

图5 关键位置荷载因子-位移曲线Fig.5 Load factor-displacement curves of key position

两种情况下获得的荷载因子分别为5.19 和6.58，取工况组合LS4 对应的荷载因子5.2 作为非线性屈曲分析结果。《空间网格结构技术规程》（JGJ 7—2010）要求网壳结构按弹性全过程分析所得安全系数K不小于4.2，按弹塑性全过程分析时安全系数K不小于2.0［6］。本文看台结构弹性全过程分析所得安全系数为8.1，弹塑性全过程分析所得安全系数为5.2。考虑到计算模型与实际结构在边界处理、连接方式、构造特点上做了一定简化处理，因此将计算所得安全系数折减一半，最终得到弹性全过程分析安全系数4.1、弹塑性全过程分析安全系数2.6。

4 现场应力及变形监测

对于1 个看台单元中的高、中、低三个区域，设置的观众席数一样，承受的上部活荷载也一样，但看台高区由于支撑柱长细比更大，二阶效应更明显，因此相对最不利。选取1 单元看台高区作为现场测试区域，监测其荷载作用下的矩管立柱应力和C 型钢主梁挠度。现场测点布置如图6 所示，共设置5 个C 型钢主梁跨中挠度测点（N1—N5）、10个立柱应力测点（A1/A2—E1/E2）。

图6 现场测点布置情况Fig.6 Measuring point position

为精确测量各种活荷载作用下看台钢结构立柱应变及C 型钢主梁变形情况，现场安排人员列席于看台座位，同一高度坐区安排14 名人员，共计7 排98 人。实测均布活荷载约为2.8 kN/m2，另外看台装饰装修及座椅等恒载约0.5 kN/m2。试验中主要模拟四种使用工况，分别为：①人员静坐于各自座位（LC1）；②人员于各自座位反复起立坐下（LC2）；③人员立于各自座位原地踏步（LC3）；④人员静坐后沿过道疏散到地面（LC4）。

4.1 监测数据汇总

图7 分别列出了四种工况下A1/A2—E1/E2柱列应力时程曲线，数据采集时长约为3 分钟。LC1 工况下各立柱应力幅值变化不大，加载呈现出基本平稳的加载过程。LC2工况下各立柱应力幅值变化较大，随人员反复起立坐下，立柱应力呈现周期变化。LC3工况下各立柱应力幅值变化剧烈，随人员有节奏地原地踏步，立柱应力呈现显著周期变化。LC4 工况下各立柱应力幅值变化不大，与LC1静坐工况下类似，人员沿走道撤离过程中立柱应力缓慢减小。

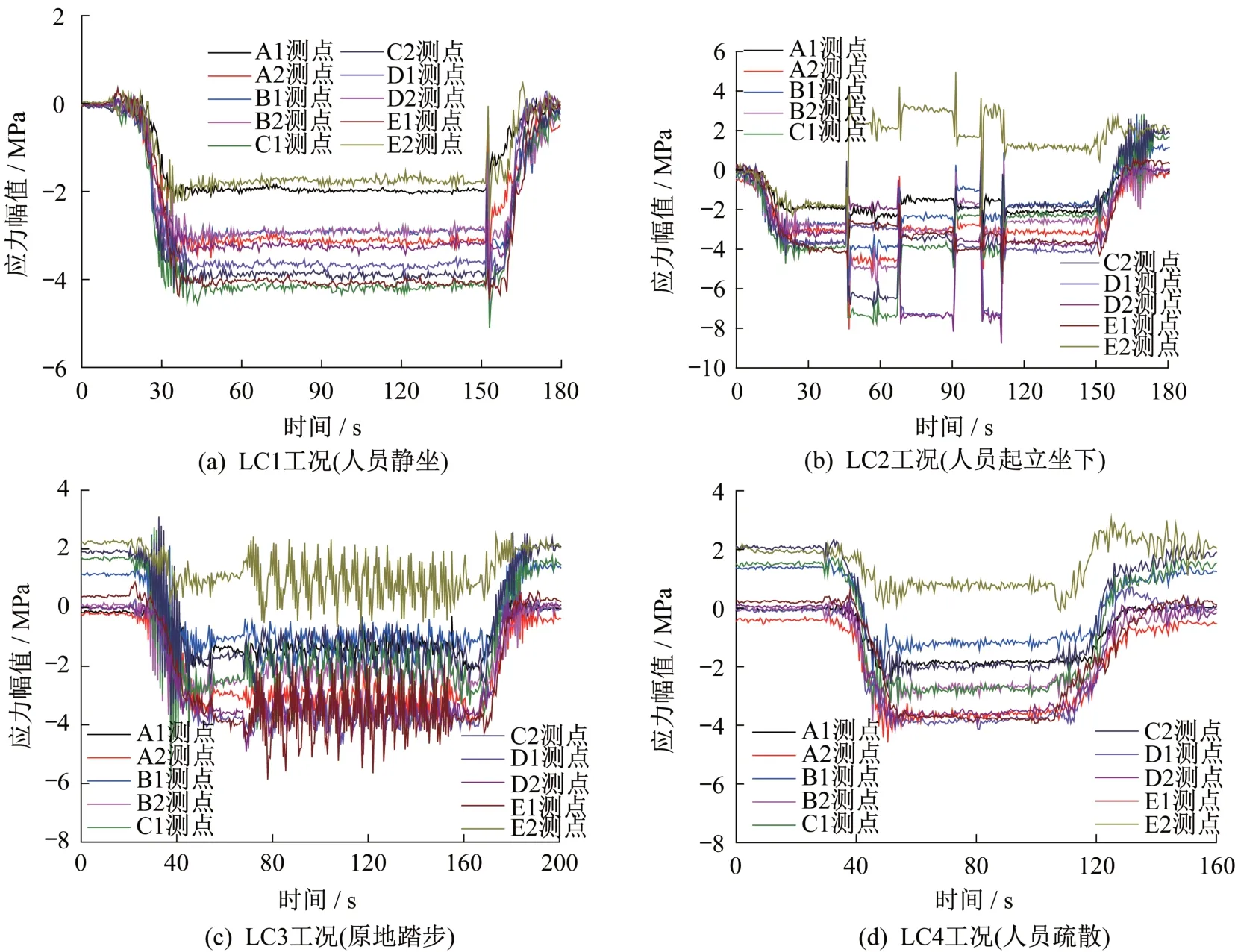
图7 立柱应力变化曲线Fig.7 Stress change curves of steel columns

图8 中四种工况下C 型钢主梁N1—N5 测点的挠度时程曲线与立柱应力变化情况相似。LC1工况下各C 型钢主梁挠度幅值变化不大，加载呈现出基本平稳的过程。LC2 工况下C 型钢主梁挠度幅值变化较大，随人员反复起立坐下，主梁挠度呈现周期变化。LC3 工况下C 型钢主梁挠度幅值变化剧烈，随人员原地踏步，挠度变化具有非常明显周期特征。LC4 工况下C 型钢主梁挠度幅值变化特征与LC1 静坐工况接近，人员撤离过程中主梁挠度缓慢减小。

图8 主梁挠度变化曲线Fig.8 Deflection change curves of steel girders

4.2 现场监测与理论计算对比

将监测得到的立柱应力及C型钢主梁挠度时程曲线中的峰值数据及有限元计算结果列于表4。实测各工况下立柱应力均较小，原地起立坐下工况（LC2）中，立柱应力最大均值为8.5 MPa。C型钢主梁挠度最大值为2.6 mm，出现于原地踏步工况（LC3）下，小于l/360（约8 mm）的挠度限值［7］。各柱列在四种工况下的实测应力值在4.4～8.5 MPa，除去E1 测点和D1 测点两个极值外，各立柱实测应力主要在5.0～7.7 MPa，均值为6.5 MPa。

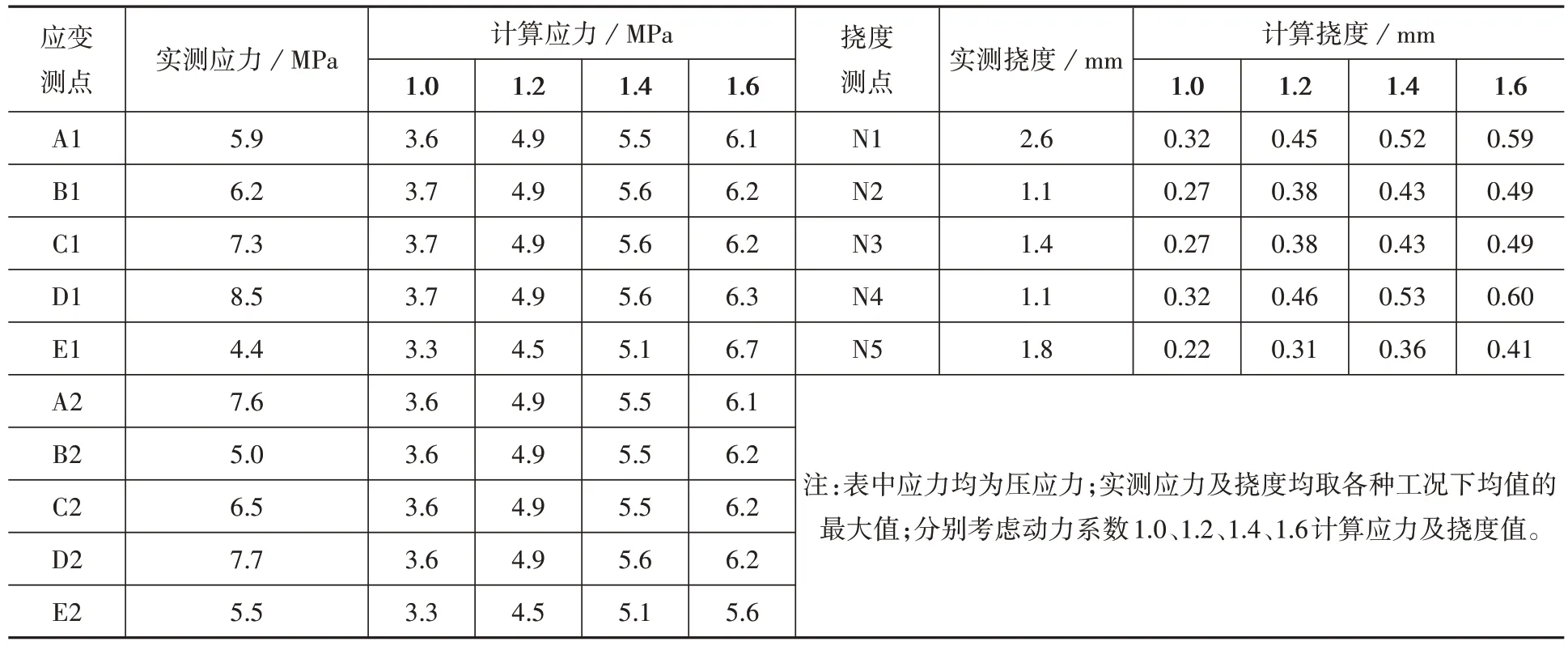
表4 现场实测值与计算值对比Table 4 Comparison between observation value and calculated value

将0.5 kN/m2恒荷载及2.8 kN/m2的实测活荷载（考虑1.2、1.4、1.6的动力系数）施加于有限元分析模型，计算相应位置立柱应力和C 型钢主梁变形。考虑活荷载动力系数为1.6 时的各排立柱计算应力值在5.6～6.7 MPa（均值为6.2 MPa），与实测立柱应力吻合较好。有限元模型将上部次梁与C 型钢主梁间连接简化为铰接，而实际连接方式为竖向搭接，故主梁跨中挠度计算值小于实测挠度。

5 结论

通过对装配式可伸缩钢结构看台力学性能的理论分析和现场监测得到如下主要结论：

（1）结构计算表明，看台立柱、主梁及支撑构件在包括恒荷载、竖向均布活荷载、竖向非均布活荷载、水平向活荷载在内的各工况组合下的最大应力比小于0.9。

（2）结构具备较好的整体稳定性能，弹性全过程分析安全系数为4.1，弹塑性全过程分析安全系数为2.6，基本满足相关规范要求。

（3）使用中立柱表面应力监测数据与理论计算结果吻合，由于模型主次梁连接简化处理导致C 型钢主梁挠度计算值小于实测值。监测及计算均表明看台关键构件应力、挠度水平较小。

（4）设计此类装配式可伸缩钢结构看台时，建议根据实际使用情况确定活荷载，同时宜考虑1.6的动力系数。