内燃动力包隔振参数灵敏度分析及优化设计

吴杨俊，徐翠强，陈杰，贺小龙，张立民

(1. 西南交通大学牵引动力国家重点实验室，四川成都，610031；2. 中车青岛四方机车车辆股份有限公司，山东青岛，266111；3. 重庆文理学院智能制造工程学院，重庆，402160)

目前，高速铁路客运广泛采用电力动车运输，但在铁路电气化水平不高的国家与地区，为了提高铁路运输能力，其铁路客运主要采用内燃动车运输。柴油发电机组为内燃动车的动力源，由于车下安装空间的限制，柴油发电机机组及其他附属设备被安装在1个基础框架上，框架通过二级隔振器与车体相连，从而构成了动力包双层隔振系统。动力包工作状态下产生的振动既会影响动力包内部设备的振动状态，也会通过隔振器传递到车体，降低乘客的乘坐舒适性，因此，动力包隔振参数的优化设计也是内燃动车组设计中不可或缺的一环。

针对双层隔振理论和技术，许多学者从不同的角度进行了大量研究[1−3]。目前，动力包双层隔振系统的隔振技术还处在初步探索和应用阶段，带有源子隔振系统的双层隔振系统隔振设计的相关研究还较少。GINA 等[4]研究了运载火箭及其子系统的隔振设计，但并没有深入探讨两者间的耦合振动特性。孙玉华等[5−7]针对内燃动车动力包双层隔振系统，建立了动力包双层隔振系统有限元模型，将解耦率、隔振效率及振动烈度作为评价指标，运用枚举法从多个设计方案中选择出满足工程要求的方案。此方法虽然取得了较好的效果，但设计效率较低、计算工作量较大，且不易获得最优参数方案。为此，时威振[8]以内燃机车动力总成为研究对象，分析了隔振系统悬挂参数对其隔振性能的影响规律，并选用基于Pareto最优解的多目标遗传算法对系统进行多目标优化设计，从而提高了设计效率。陈俊等[9]研究了子系统对双层隔振主系统固有特性的影响规律，并对子系统设计提出了合理建议。

从以上研究成果可以看出，目前，针对内燃动力包双层隔振系统设计并未形成统一的标准或者行业规范。由于动力包隔振参数优化设计涉及变量较多，导致优化设计过程中计算量较大，设计效率较低。为解决上述问题，本文将全局灵敏度分析方法引入动力包隔振参数设计中，通过全局灵敏度方法确定对动力包隔振性能影响较大的参数，并将其作为优化变量对动力包隔振参数进行优化设计，以期有效缩减设计中所需的优化变量，提高优化效率。

1 内燃动力包系统数学建模

以某型号内燃动力包双层隔振系统(见图1)为研究对象，建立内燃动力包数学模型，该模型包含1个框架(图2(a))、1个柴油发电机组(图1(b))和1个冷却风机(图2(c))。动力包模型含有11 个隔振器，其中包括机组与框架连接处的3个一级隔振器(布置在a1，a2和a3悬挂点)，冷却装置与框架连接处的4 个一级隔振器(布置在a4，a5，a6和a7悬挂点)以及框架与基础连接处的4 个二级隔振器(布置在b1，b2，b3和b4悬挂点)。

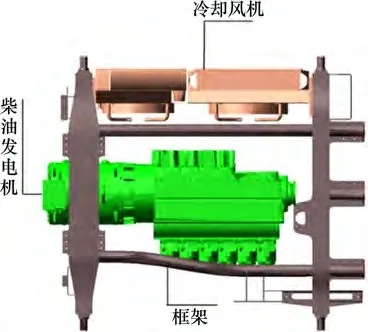
图1 动力包结构俯视图Fig.1 Top view of power pack structure

图2 动力包各部件平面图Fig.2 Plane view of each part of power pack

内燃动力包振动模型的18 个自由度分别为：框架沿x，y和z方向平动的自由度xo1，yo1和zo1；过框架质心o1绕x，y和z方向的转动自由度αo1，βo1和γo1；柴油机沿x，y和z方向平动的自由度xo1，yo2和zo2，过机组质心o2绕x，y和z方向的转动自由度αo2，βo2和γo2；冷却风机沿x，y和z方向平动的自由度xo3，yo3和zo3，过冷却风机质心o3绕x，y和z轴的转动自由度αo3，βo3和γo3。动力包物理参数见表1。

常规的内燃动力包隔振系统设计一般将各个隔振器三向刚度作为优化变量。为减少设计变量的数量，本文将各个隔振器垂向刚度、横垂比(隔振器横向刚度与垂向刚度比值)、纵垂比(隔振器纵向刚度与垂向刚度比值)作为设计参数，同时，动力包各参数计算值由相关合作单位提供，见表1。

表1 动力包物理参数Table 1 Physical parameter of power pack

根据振动理论可得出柴油发动机沿x，y和z轴平动自由度的振动方程为

柴油发动机绕x，y，z轴转动自由度的振动方程为

式中：Faix，Faiy和Faiz分别为ai隔振器在x，y和z方向的作用力；Fo2x，Fo2y和Fo2z分别为作用在柴油机x，y和z轴上的激振力；Mo2x，Mo2y和Mo2z分别为作用在柴油机x，y和z轴上的激振力偶。

冷却风机沿x，y和z轴平动自由度的振动方程为

冷却风机绕x，y和z轴转动自由度的振动方程为

式中：Fo3x，Fo3y和Fo3z分别为作用在冷却风机x，y和z轴上的激振力；Mo3x，Mo3y和Mo3z分别为作用在冷却风机x，y和z轴上的激振力偶。

框架沿x，y和z轴平动自由度的振动方程为

框架绕x，y和z轴转动自由度的振动方程为

式中：Fbix，Fbiy和Fbiz分别为bi隔振器在x，y和z方向上作用力。

2 动力包系统振动响应及隔振性能指标的计算方法

2.1 动力包系统数值求解方法

本文采用翟婉明[10]提出的新型快速显示数值积分法求解车辆系统的振动响应，假设系统在t=(h+ 1)Δt瞬时的振动方程为

式中：M为系统的质量矩阵；Kh+1和Ch+1分别为第h+1 步迭代系统的刚度与阻尼矩阵；Ph+1为第h+1步迭代系统的广义载荷矢量；为第h+1步迭代系统的广义加速度矢量；为第h+1步迭代系统的广义速度矢量；Xh+1为第h+1步迭代系统的广义位移矢量。Δt为时间积分步长，φ与φ为控制参数。

系统初始条件为

根据式(7)～(9)逐次求出各迭代步的位移、速度与加速度离散值。起步时只需令φ=φ= 0，则可使本方法具有积分“自开始”的特性。

2.2 动力包机组振动烈度求解方法

机组振动烈度反映了柴油发电机组自身振动环境，若机组振动烈度过大，则会严重影响机组工作质量并缩短其使用寿命[8]，因此，可将动力包机组振动烈度作为系统隔振性能评价指标之一。参照TB/T 3164—2007“柴油机车车内设备机械振动烈度评定方法”[11]中柴油发电机组测点布置规定，结合该柴油发电机组结构特点，机组振动烈度的测点位置Du(u=1～8)分布如图3所示。

图3 振动烈度考核点位置分布Fig.3 Location distribution of vibration intensity measurement points

基于动力包机组振动烈度测点位置，可得机组振动烈度Vrms计算公式：

式中：VrxDu，VryDu和VrzDu分别为测点Du(u=1～8)在x，y和z方向的均方根速度。

2.3 动力包系统隔振效率求解方法

动力包双层隔振系统设计的目的之一是最大限度地减少内部设备激励的传递，避免动力包与车体之间的振动耦合，提高整车的乘坐舒适性[5]。动力包系统隔振效率能够反映系统激励传递到车体上的衰减情况，可作为动力包隔振性能评价指标。根据文献[5]可知内燃动力包系统传递到基座上的当量力F为

式中：Frbix，Frbiy与Frbiz(i=1～4)分别为bi处隔振器在x，y和z方向上的力的均方根值；Nx，Ny，Nz分别为各隔振器在x，y，z这3个方向上的测点个数。

由于动力包内部激励既含有激振力又含有激振力矩，因此，在计算动力包隔振效率之前，需将内部激励转化为基座上4个隔振器的三向力，即动力包内部激励与4个隔振器上的三向力处于平衡状态。根据超静定方程可获得内部激励转化到基座上4个隔振器的三向力，进而得到转化后的激励当量力F0为

式中：F′rbix，F′rbiy与F′rbiz(i=1～4)分别为内部激励转化到bi处隔振器的力在x，y和z方向上的均方根值；

动力包系统的隔振效率η为

3 动力包隔振参数全局灵敏度分析

为研究动力包各隔振参数对动力包隔振性能影响的程度，进而确定影响系统隔振性能的主要参数，需对系统隔振参数进行灵敏度分析。早期主要使用的是局部灵敏度分析法，此类方法概念明确，计算方便，但鉴于其是以微分或差分理论为基础，因此，系统结构参数的变动范围不能过大。当系统非线性特征较强或者参数变化范围较大时，局部灵敏度分析方法往往不能得出有效结果[12]。为克服局部灵敏度分析法所存在的缺陷，全局灵敏度分析法应运而生[13]。Sobol 法[14]是一种基于方差的全局灵敏度分析法，该方法能够快速简便地计算出高阶交叉影响项，目前已被广泛应用于经济、环境、生物、物理、化学、控制及神经网络等领域的研究。

3.1 Sobol灵敏度分析法原理

定义单位区间I为[0,1]，In为n维超立方单元体，假设函数f(g)的变量g=(g1,g2,g3,…,gn)，g∈In，可将函数f(g) 看作是2n个递增子项之和[14]：

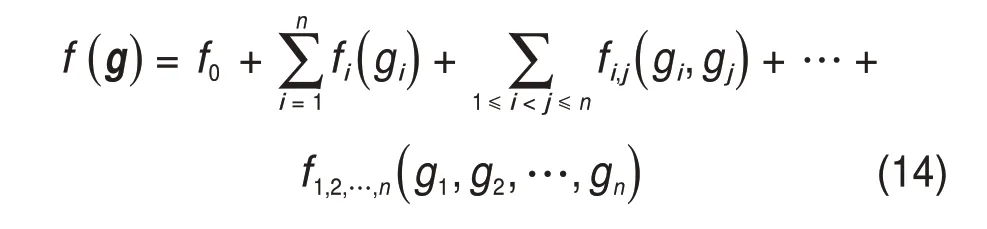
式中：f0为期望。

假设q={g1,g2,…,gm}⊂{g1,g2,…,gn},同时Mq={1,2,…,m}， 其补集v={g1,g2,…,gn}q，Mv={1,2,…,n}Mq，q的一阶和高阶灵敏度表达式为式中：D为函数f(g)的总方差；Dv为v的偏方差；Dq为q的偏方差；Sv为v的一阶灵敏度；Sq和S分别为参数q的一阶灵敏度与高阶灵敏度，其中高阶灵敏度也可称为总灵敏度，0 ≤Sq≤≤1。当Sq== 1 时，f(g) 只与q有关；当Sq== 0时，f(g)与q无关。

按式(15)直接计算灵敏度会碰到很多困难，因此，Sobol 灵敏度可运用蒙特卡罗积分获得，计算公式如下：

式中：gi=(qi,vi)和g′i=(q′i,v′i)为2 组样本数据；i= 1,2,…,N；N为采样点数。

将式(16)中的Dv，D和Dq代入式(15)可得到相应q的一阶和高阶灵敏度。

参数的一阶灵敏度只反映了此参数单独变化时对目标函数的影响程度，参数的高灵敏度不仅反映了该参数单独变化的影响，也反映了该参数与其他所有参数的交互作用对目标函数的影响。

3.2 动力包系统隔振参数灵敏度结果分析

采用Sobol法分析各隔振参数对动力包隔振性能的影响程度时，需给定参数的变化区间。各参数的取值范围见表2。

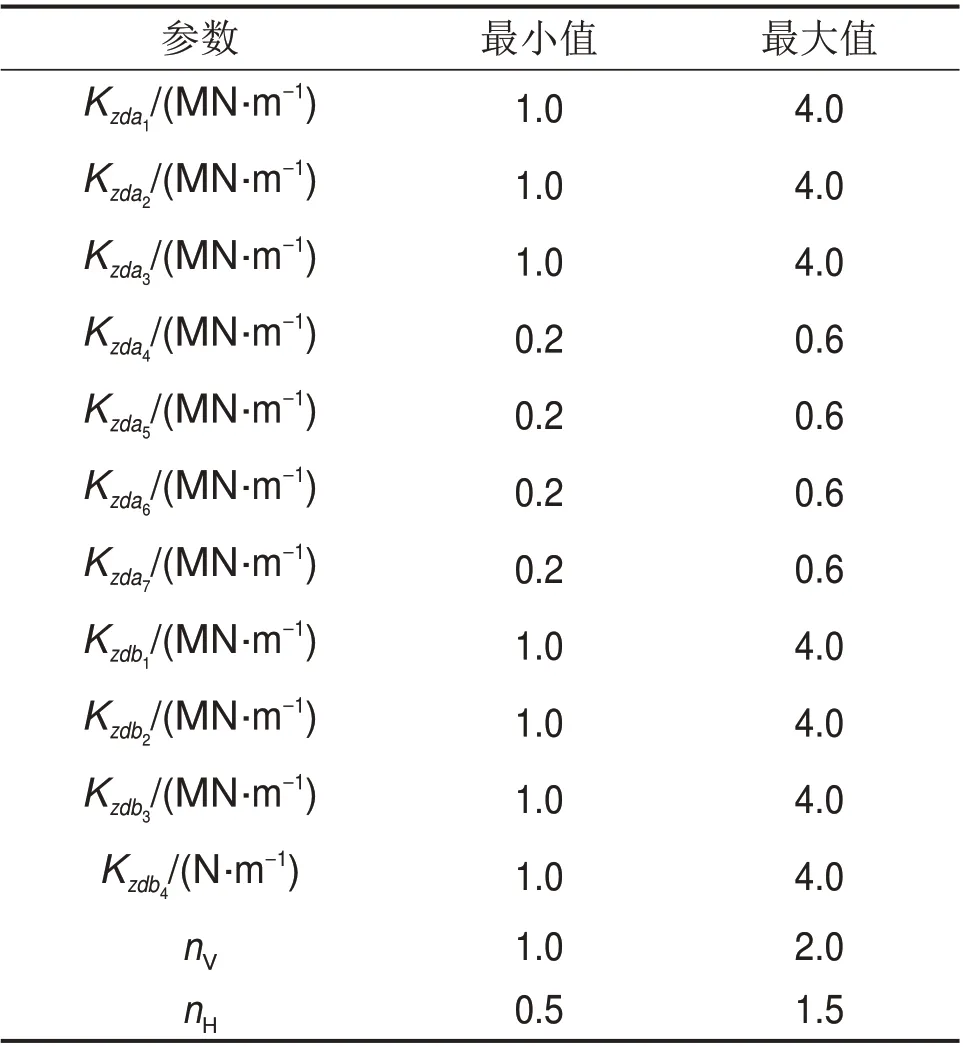
表2 动力包隔振参数取值范围Table 2 Value range of vibration isolation parameter of power pack

基于动力包18自由度数学模型，运用Sobol法计算得到不同转速工况下动力包各隔振参数对2个隔振性能指标的一阶与高阶灵敏度。

图4和图5所示分别为各个转速工况下动力包各隔振参数对机组振动烈度的一阶与高阶灵敏度分布。图中工况1 对应转速为1 000 r/min(空载)，工况2～10 分别对应转速为1 000，1 100，…，1 800 r/min(负载)。

从图5可以看出：随着动力包转速增加，nV与nH的高阶灵敏度整体上呈增大趋势。此外，从图4和图5可以看出，一阶灵敏度与高阶灵敏度所反映的情况不完全相同，例如，当动力包转速工况为1 700 r/min(负载)时，nV的一阶灵敏度比nH的大，而nV的高阶灵敏度比nH的小，这是因为一阶灵敏度并不能反映评价参数与其他参数的交互作用对目标函数的影响。从图4和图5看出，对机组振动烈度而言，一阶与高阶灵敏度较大的参数为Kzda1，Kzda2，Kzda3，Kzdb1，Kzdb2，Kzdb3，Kzdb4，nV和nH。

图4 隔振参数对机组振动烈度的一阶灵敏度Fig.4 The first-order sensitivity of vibration isolation parameters to unit’s vibration intensity

图5 隔振参数对机组振动烈度的高阶灵敏度Fig.5 High-order sensitivity of vibration isolation parameters to unit’s vibration intensity

图6和图7所示分别为各个转速工况下动力包各隔振参数对系统隔振效率的一阶与高阶灵敏度分布情况。

图6 隔振参数对系统隔振效率的一阶灵敏度Fig.6 The first-order sensitivity of vibration isolation parameters to vibration isolation efficiency

图7 隔振参数对系统隔振效率的高阶灵敏度Fig.7 High-order sensitivity of vibration isolation parameters to vibration isolation efficiency

从图6和图7可以看出，在1 000 r/min(空载)与1 000 r/min(负载)工况下，对系统隔振效率而言，一阶灵敏度最大的参数为Kzdb4，而高阶灵敏度最大的参数为Kzda3，可见一阶灵敏度对参数影响程度的评价结果存在误差。从图6和图7还可以看出，对于系统隔振效率而言，一阶与高阶敏度较大的参数为Kzda1，Kzda2，Kzda3，Kzdb1，Kzdb2，Kzdb3，Kzdb4，nV和nH。

内燃动力包系统隔振参数全局灵敏度分析结果表明，在所有转速工况下，冷却风机上4个一级隔振器垂向刚度对系统2个隔振性能指标的灵敏度较小，而其他9个参数对系统隔振性能指标的灵敏度较大，因此，可将这9个参数作为影响动力包系统隔振性能的主要参数。

4 动力包隔振参数优化设计

4.1 优化变量

根据第3节动力包隔振参数灵敏度分析结果可知，影响机组振动烈度与系统隔振效率的主要参数为Kzda1，Kzda2，Kzda3，Kzdb1，Kzdb2，Kzdb3，Kzdb4，nV和nH，因此，本文将横垂比、纵垂比、机组a1，a2和a3以及框架b1，b2，b3和b4悬挂点上的隔振器的垂向悬挂刚度作为优化变量，优化变量U可以表示为

4.2 优化目标函数的建立

将动力包机组振动烈度作为优化目标之一，基于本文2.2节中振动烈度计算公式，可得到机组振动烈度目标函数J1为

同理，动力包系统隔振效率也可作为优化目标之一。同时，为使2个目标函数都以最小值为最优，将目标隔振效率转化为力传递率，基于本文2.3 节中隔振效率计算公式，可得到系统力传递率目标函数J2为

为满足工程需求，系统的隔振效率需大于80%，即力传递率要小于20%。同时机组振动烈度应该为B 级或A 级(Vrms≤0.018 m/s)。为便于计算，需运用加权系数法将多目标函数问题转化为单目标函数问题，由于2个目标函数存在差别，需对目标函数进行归一化处理：

式中：λ1和λ2为加权因子，且有

如果没强调以某一目标为主要优化目标，那么2个加权因子均取0.5。

4.3 约束条件

4.3.1 模态频率匹配约束

根据隔振理论可知，为避免隔振系统激励频率与模态频率出现共振现象，同时保证系统具有良好的隔振效果，系统的激励频率与模态频率的比值应该大于，若工程要求激励频率必须小于模态频率时，则激励频率与模态频率的比值应该小于。其约束条件为

式中：ωj为第j个激励频率，ωi0为系统第i阶模态频率。

4.3.2 静平衡条件约束

为防止动力包发生倾覆，要求装车后机组与安装框架不产生较大倾斜，因此，要求相同部件上的同级隔振器垂向静压缩量差不超过1 mm[15]；此外，由于车下安装空间限制，还需将一级隔振器的垂向静压缩量范围控制在2～7 mm，并且二级隔振器的垂向静压缩量范围控制在3～9 mm。其约束条件如下：

式中：Zbl和Zae分别为悬挂点bl和ae上隔振器的垂向静压缩量，其中l取值范围为1～4，e取值范围为1～7。

本文采用的隔振器为橡胶隔振器，其动静比(动刚度与静刚度的比值)取值范围一般为1.3～1.6[16]，本文橡胶隔振器动静比取为1.5。通过上述静平衡约束可对各隔振器的静刚度进行约束，进而结合动静比对各隔振器的动刚度进行约束。

4.4 动力包隔振参数优化分析

基于本文所建内燃动力包优化模型，在转速为1 800 r/min(负载)激励条件下，运用遗传算法对动力包系统进行优化设计。

图8所示为各代种群中所有个体的最佳适应度值与平均适应度的变化曲线，种群中所有个体的最佳适应度随种群迭代数不断下降，同时可以看出45代之后，最佳适应度趋于稳定，直到75代时满足终止条件，其种群最佳适应度为0.538，因此，可认为遗传算法优化过程达到了收敛状态。

图8 适应度曲线Fig.8 Fitness curves

表3 所示为内燃动力包参数优化前后的取值。图9 和图10 分别为不同转速工况下内燃动力包中柴油发电机组振动烈度与系统隔振效率优化前后结果对比。图11 所示为系统各隔振性能指标在不同转速工况下的变化幅度。

表3 优化前后动力包隔振参数Table 3 Vibration isolation parameters of power pack before and after optimization

从图9可以看出，参数优化后，各工况下的机组振动烈度明显降低且都小于0.018 m/s。

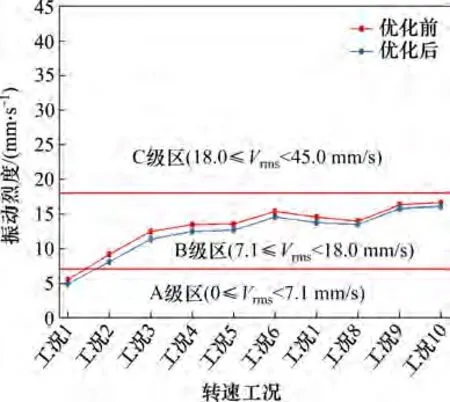
图9 机组振动烈度优化前后对比Fig.9 Comparison of unit's vibration intensity before and after optimization

从图10 可见，参数优化后，系统的隔振效率得到了显著提升且各工况下的隔振效率都达到了85%以上。

图10 隔振效率优化前后对比Fig.10 Comparison of vibration isolation efficiency before and after optimization

从图11 可知，不同工况下机组振动烈度与系统隔振效率的变化幅度趋势相近，且都在1 000 r/min(空载)工况时变化幅度最大，分别达到了12.00%与29.61%。

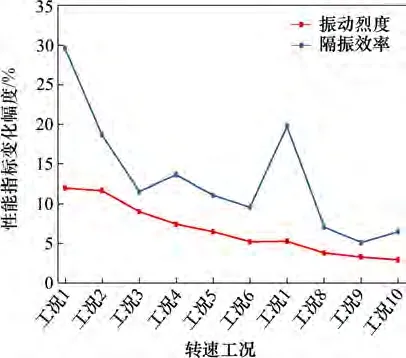
图11 隔振性能指标变化幅度Fig.11 Change amplitudes of index of vibration isolation performance

综上所述，经过优化设计后的内燃动力包隔振系统的振动烈度明显下降，系统隔振效率明显提升，说明此优化方法是可行的。

5 动力包隔振性能试验与仿真结果对比分析

将动力包安装于地面台架上(见图12)，对各工况下动力包隔振性能进行测试，其中各隔振器刚度为本文第4节所提优化设计的刚度。

图12 动力包台架Fig.12 Platform of power pack

5.1 机组振动烈度试验与仿真对比分析

图13所示为振动烈度测点D5在各转速工况下的三向加速度振动信号。

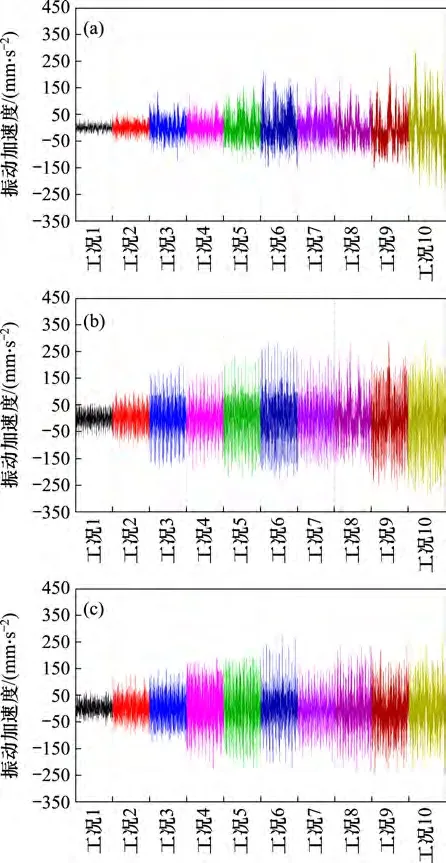
图13 D5点三向加速度振动信号Fig.13 Three-directional acceleration vibration signal of measuring point D5

实验测试结束后，获取各测试点的加速度响应信号，并通过积分将加速度信号转变为测点速度信号，分别求出各个测点在测试时间段内的三向速度，从而得到动力包机组振动烈度。

图14 所示为柴油发电机组振动烈度实验值与仿真值对比。从图14 可以看出：振动烈度实验与仿真结果相近，且变化趋势一致。由于仿真模型将动力包隔振系统考虑成纯刚体模型，而实验中的动力包系统是柔性模型，柔性构架在动力包运行过程中会产生一定的弹性振动，导致仿真结果与实验结果产生了一定偏差。实验结果表明，动力包在1 000 r/min空载与负载2个工况下机组振动烈度的等级达到A级，其他工况下都达到B级。测试结果表明，本文设计的动力包结构机组振动烈度满足工程要求。

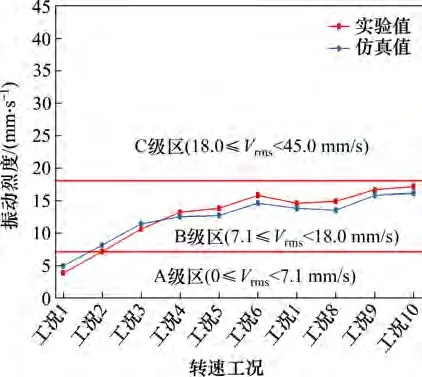
图14 机组振动烈度实验值与仿真值对比Fig.14 Comparison of experiment values and simulation values of unit's vibration intensity

5.2 动力包隔振效率试验与仿真对比分析

分别在4个二级隔振器b1，b2，b3和b4的上下2 个位置各布置1 个测点，从而测得隔振器上下测点加速度时域信号，再通过二次积分得到相应测点的位移时域信号，接着将各个二级隔振器上下测点的位移差与对应隔振器的刚度相乘即可以求出传递到基础框架上的力时域信号，从而获得本次地面台架实验动力包系统的隔振效率。

图15 所示为动力包隔振系统的隔振效率实验值与仿真值对比。从图15 可以看出：隔振效率仿真结果与实验结果偏差较小，并且变化趋势相近；各工况下动力包系统隔振效率都在85%以上；当转速在1 000 r/min(负载)以上时，系统隔振效率均在90%以上。实验结果表明，本文设计的动力包双层隔振系统在各工况下都具有良好的隔振效果。

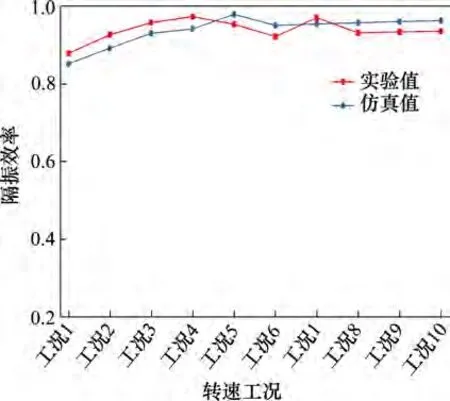
图15 机组隔振效率实验值与仿真值对比Fig.15 Comparison of experiment and simulation values of vibration isolation efficiency

6 结论

1)对机组振动烈度与系统隔振效率而言，灵敏度较大的参数变量为Kzda1，Kzda2，Kzda3，Kzdb1，Kzdb2，Kzdb3，Kzdb4，nV和nH。因此，上述参数可作为动力包系统隔振性能的主要影响参数。

2)与优化前相比，优化后的动力包系统各个工况下的隔振性能得到了显著改善，在1 000 r/min(空载)工况下，机组振动烈度降低了12.00%，系统的隔振效率提升了29.61%。

3) 所有工况下动力包机组的振动烈度都为B级或A 级，且系统隔振效率都在85%以上，满足工程要求。同时，动力包2个隔振指标的实验结果与仿真结果差异较小，且变化趋势一致，验证了内燃动力包隔振系统数学模型的准确性及系统隔振参数优化设计方法的可行性。