优化凿孔极化码在NAND FLASH 中的纠错技术研究

宋燕娜，郭 锐

（杭州电子科技大学通信工程学院，浙江杭州 310018）

0 引言

随着现代科技的飞速发展，关于存储器的发展也一直是热点话题，其已融入人们生活的方方面面。存储器可分类为易失［1］和非易失［2］两类，NAND FLASH（简称为闪存）属于后者，即断电后数据能够存储。闪存的存储单元在发展过程中由于对存储容量的高要求而不断增加［3-4］。但存储密度增加的同时，也带来了更大的噪声［5-6］。因此，当闪存由于不可避免的噪声干扰而一再损害存储数据可靠性时，就需要引入纠错码（Error Correcting Code，ECC）以保证闪存数据读取正确性。

极化码［7］相较于其他信道编码具有更为出色的纠错能力，它的编译码复杂度都较低，且能被证明可以达到信道容限。因此，利用极化码对闪存进行读数纠错成为一大研究热点。文献［8］提出一种基于极化码构造的新编码方案，它支持任意数量的重写并能够纠正大量错误；文献［9］研究了闪存的可靠性和持久性问题，并且设计了针对闪存中非对称错误的极化码纠错方案，完成了对闪存的一次性大量纠错；文献［10］提出通过缩短非系统极化码和系统极化码的方法，构造码率匹配的极化码应用于闪存，提高了闪存的可靠性；文献［11］设计了在固态硬盘（Solid State Drives，SSDs）中的多速率极化码，由于SSDs 中的存储单元主要由闪存组成，因此该研究提高了极化码对闪存的纠错性能。为了使极化码更好地满足闪存高码率的要求，且可以在闪存的数据纠错应用上具有更好的性能，本文对极化码进行了优化巴氏参数构造和凿孔操作以构造新码字。

本文以MLC 闪存为例，以闪存阈值电压分布模型为基础，使用非均匀存储感知法计算重叠区域的相邻边界值和感知电压，进而计算每个存储比特的对数似然比（Log likelihood ratio，LLR），并将其拟合成高斯分布并得到方差。通过迭代计算每个存储单元位的巴氏参数，并且根据闪存页容量和已知的元数据信息构造码率匹配的极化码，使之可以更好地应用于闪存的纠错模型中。本文所用的优化巴氏参数方法构造的码字性能与高斯近似构造方法相比，在构造（136，128）、（272，256）、（550，512）凿孔码字时分别有2.32、2.1、1.7dB 的性能增益，与蒙特卡洛法相比分别有0.12、0.13、0.15dB 的增益，且码长越长纠错性能越强；改变闪存的阈值电压分布，可以得出如下结论：极化码的纠错性能随着闪存擦除单元标准差的减小而增强。

1 MLC 闪存基本理论

1.1 MLC 闪存基本结构

一个或N 个平面组成闪存，多个块（Block）又组成一个平面，每块包含多页（Page），多个存储单元组成一页，其中读写操作主要在页中进行，而擦除操作主要在块中进行。在闪存的每页中有数据区和数据冗余区，图1 中Page 代表的是数据区，用来存储有用的用户信息。此外，闪存中还有oob 区域（附加数据空间），进行闪存的纠错校验，用于存放元数据信息，在闪存中存储的固件所用的临时数据和信息通常被称为元数据［12］。

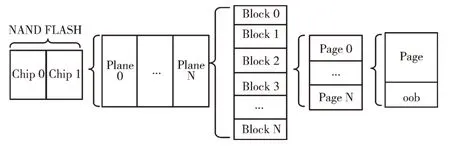
Fig.1 NAND FLASH component unit图1 闪存组成单元

闪存中最常用的是MLC 闪存，在一个存储晶体管中存储两位数据，通过图2 可以看出，闪存由源极、漏极、控制栅、氧化绝缘层和浮动栅组成。闪存拥有双层浮栅，外层有一个控制栅，保证闪存的可靠性；内层有一个浮动栅［13］，它的作用是对电荷的收放，而浮动栅外有氧化绝缘层，它可以保护浮栅门不轻易吸收或释放电荷，尤其是在没有电源供电的情况下，这就是存储器的非易失性。浮动栅中还有不同状态的存储单元，闪存的本质就是对这些电压进行探测和感知［14］。

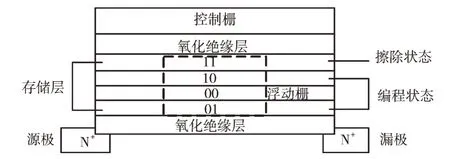
Fig.2 MLC NAND FLASH storage structure图2 MLC 闪存的存储结构

闪存的基本操作主要有擦除、编程（写入）和读取。闪存可以读/写一个页，但是必须以块大小擦除。可以近似将擦除状态的阈值电分布类比为高斯分布，可以近似表示为如式（1）所示，μS0和σS0是擦除状态阈值电压分布的均值和标准差。

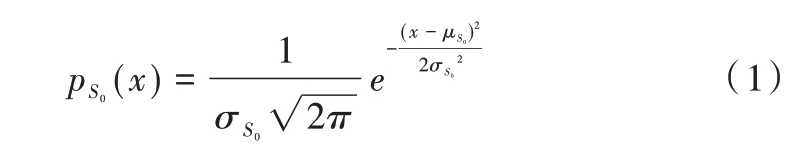
闪存的另一个重要操作就是写入操作，在闪存中写入操作就是页的编程操作。对于编程过程，增量步脉冲编程（ISPP）技术被广泛应用，如图3 所示。因此，编程状态的阈值电压可以看作是[Vp,Vp+ΔVpp]上的均匀分布，其中，Vp和ΔVpp分别表示校验电压和编程步进增量电压［15］。第k个编程状态阈值电压的边界Vp和Vp+ΔVpp分别用Vl(k)和Vr(k)表示，则编程状态的阈值电压分布表示为如式（2）所示。

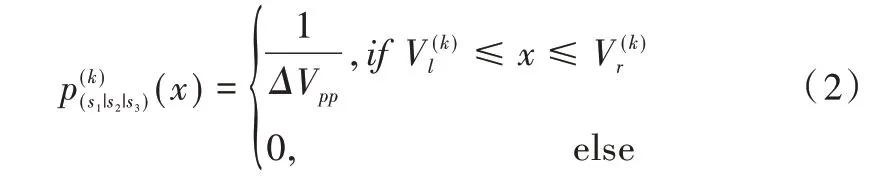
但是均匀分布只是一种理想中的情况，当闪存没有噪声干扰时可以实现，但实际情况下，闪存存在各种噪声干扰，因此如式（2）所示对编程状态阈值电压分布的模拟并不准确。

Fig.3 Programming/check recursive programming operations图3 编程/校验递归编程操作

闪存的第3 种基本操作是对数据的读取操作［16-17］，闪存中数据读取写入的基本单位都是页。数据通过闪存存储以后，若浮栅门晶体管的阈值电压判定较为准确，写入的数据就可以被读取且错误概率较小。尤其是若浮动栅极的阈值电压能够确定，电流在通过闪存单元时，即可更高效可靠地读取闪存中存储的数据。

1.2 MLC 闪存干扰源与信道模型

单元间干扰（Cell-to-cell interference，CCI），顾名思义，既是不同单元之间因为互相影响而产生干扰。闪存中则是相邻的存储单元之间由于重叠区域而对彼此产生损害［18］。这些损害会影响阈值电压的探测精度，使得探测到的感知电压发生偏移，在闪存的几种干扰中，它拥有最大的危害。图4 表示了受损害单元的位置与损害单元的字线和位线的位置。一个受损害单元主要受到它相邻字线3 个位线上单元的损害。

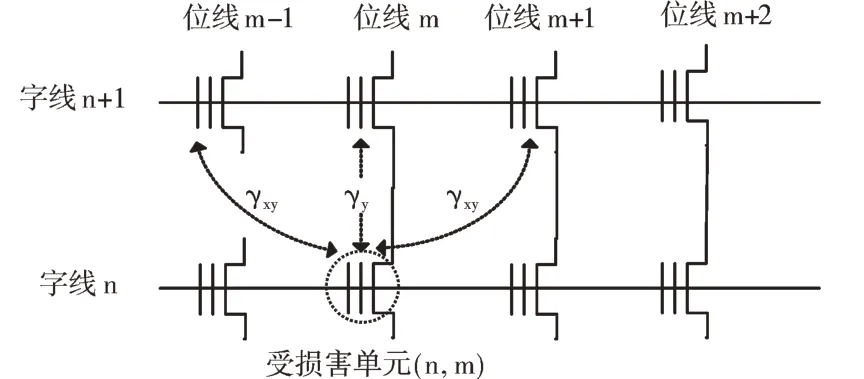
Fig.4 Intercell interference of full bit line structure图4 全部位线结构的单元间干扰

从图4 可以看出，在闪存中，字线n和位线m相关联的位置位于（n，m），因此由单元间干扰引起的受害单元的MLC 闪存阈值电压变化F 可以估算如式（3）所示。

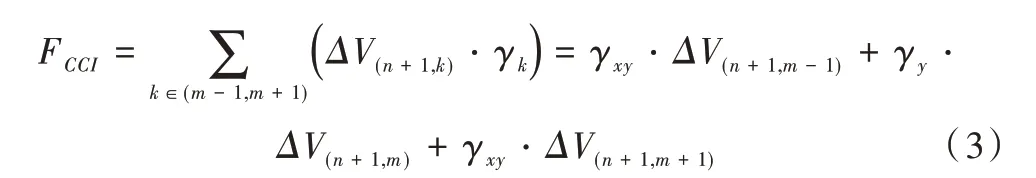
其中，ΔV(n+1,k)是在编程操作期间第n个干扰单元的阈值电压偏移，γk是受害单元与干扰单元之间的耦合比。γxy和γy分别表示斜对角线方向和90°方向的电容耦合系数。

闪存的阈值电压不仅受CCI 的影响，也容易受到其他干扰，比如编程/擦除（Program/Erase，P/E）循环，它会导致闪存产生坏块。本文分别简要介绍P/E 循环的主要干扰源［19］，即随机电报噪声（Random Telegraph Noise，RTN）和数据保留噪声（Data Retention Noise，DRN）。

关于RTN 的形成过程如下：由于在P/E 循环过程中，在靠近界面的电荷陷阱位置发生的电子捕获和发射事件，会导致阈值电压转移和波动。在达到一定数量的编程周期后，闪存单元的氧化层也将受到损伤，使得闪存的持久性下降。RTN 的阈值电压分布模型pRTN(x)可以建模为参数λr的对称指数函数，如式（4）所示。

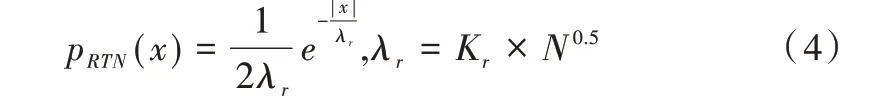
其中，λr表示循环次数并且不是递减函数，N 表示P/E循环次数，Kr是一个常量。

在经过较长时间的存储和多次P/E 循环后，电荷发生泄露，减弱了数据保留能力，即闪存保持电荷的能力降低或受到限制。由于界面陷阱恢复和电子去陷阱而导致的阈值电压降低，DRN 的阈值电压分布模型pDRN(x)可以近似建模为高斯分布，如式（5）所示。

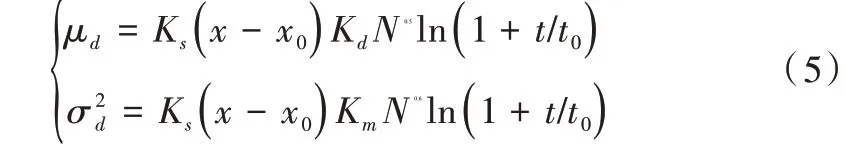
其中，μd表示其均值，表示其方差；Ks、Kd、Km是常量，x0表示闪存处于擦除状态时阈值电压初值；t 表示记忆保留时间，t0是初始时间。

首先通过对闪存的擦除操作，将去除浮栅门晶体管中的所有电荷，使得阈值电压分布都一致，再对闪存进行编程操作，将数据写入闪存中，通过闪存的传输信道，经历了CCI、RTN 及DRN 噪声，可以得到闪存的最终阈值电压分布，并且将写入的数据读取出来，如图5 所示。

Fig.5 MLC NAND FLASH channel model图5 MLC 闪存信道模型

根据上述不同干扰下的阈值电压分布公式，可得到最终的噪声阈值电压分布pf(x)如式（6）所示。

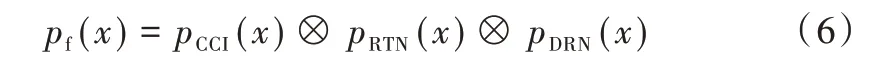
使用Matlab 进行仿真，其中MLC 闪存阈值电压分布模型的参数设置如表1 所示［20］。

根据表格中的数据可以得到闪存阈值电压在CCI、RTN 和DRN 后的概率密度图，如图6 所示。

可以看到，闪存在经过不同的干扰后受到的阈值电压偏移量和偏移方向都不同，这些结果清楚地显示了NAND闪存的动态特性。

Table 1 MLC NAND FLASH threshold voltage distribution model parameters表1 MLC 闪存阈值电压分布模型参数

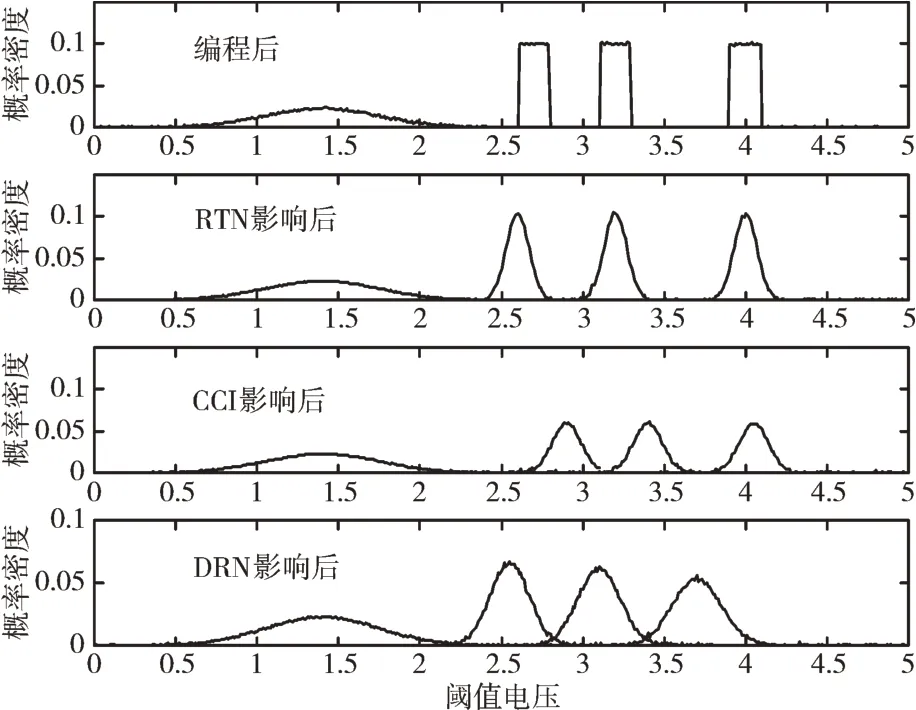
Fig.6 MLC NAND FLASH final threshold voltage distribution model after RTN，CCI and DRN effects图6 MLC 闪存经过RTN、CCI 和DRN 影响后的最终阈值电压分布模型

2 基于极化码的MLC 闪存差错控制

以下是闪存的差错控制过程：首先将待存储的信息序列输入ECC 编码器进行编码，然后在闪存页中进行编程操作，将编码后的码字信息写入闪存有噪传输信道，接着从闪存中读取存储的数据，读取后将该数据输入ECC 译码器，检查错误并且将错误纠正，输出译码后的信息序列（见图7）。本文主要介绍适用于MLC 闪存的极化码编译码方法并对其进行差错控制。

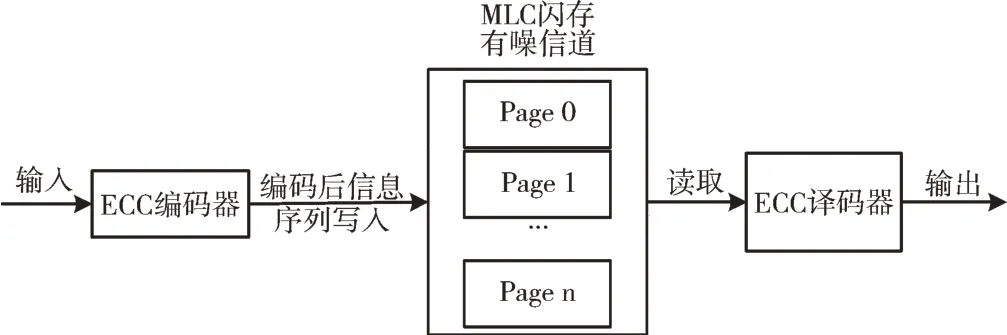
Fig.7 MLC NAND FLASH error correction model图7 MLC 闪存的纠错模型

2.1 MLC 闪存非均匀存储感知法与LLR 计算

在2 bit/cell 的MLC 闪存中，有4 种不同的状态信息分布在存储单元中，需要将它们不重叠地分离开，划分成不同的电压区间，因此需要3 个硬判决参考电压。非均匀存储感知法与传统的均匀感知法相比，在减少存储感知等级数量的同时，也能保证数据的准确性。

因此，本文在读取MLC 闪存中存储的阈值电压时可以利用非均匀存储感知法，使得在减少存储感知等级数量的同时，使数据可靠性更高，如图8 所示。主要重叠区域的边界分布在硬判决参考电压两侧，而硬判决对感知精度的要求则更高。重叠区域受单元间干扰更强，因此会对闪存的感知电压能力造成更大影响，而非重叠区域则相对没有那么大的影响。本文采用非均匀存储感知法，以实现对闪存电压更好的感知。

Fig.8 Non-uniform storage perception strategy图8 非均匀存储感知策略

从图8 可以看出，使用非均匀存储感知法，需要计算重叠区域的闪存阈值电压相邻的边界值，可以通过式（7）计算，分别设为左右相邻状态主要重叠区域的边界电压，将第a（a=0，1，2）个存储状态的阈值电压分布与相邻的相除，设定系数Q，就可以得到边界电压。

接下来将描述LLR 值的计算过程，可以将存储单元的阈值电压准确地映射成对数似然比LLR。第k个存储状态对应阈值电压的概率密度函数表示为p(k)(x)（k=0，1，2，3）。Si表示第i个比特为0 的存储状态的集合。因此，给定存储单元的阈值电压Vth，可以按式（8），计算出每一个比特的LLR。

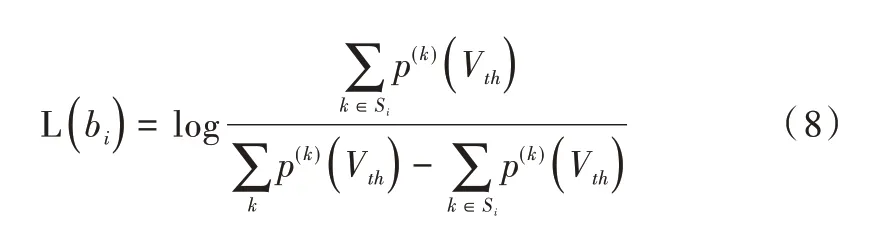
当闪存经受了CCI、RTN、DRN 干扰后，它处于擦除状态的阈值电压概率密度函数表示如式（9）所示。

当闪存经受了CCI、RTN、DRN 干扰后，它处于编程状态的阈值电压概率密度函数表示如式（10）所示。

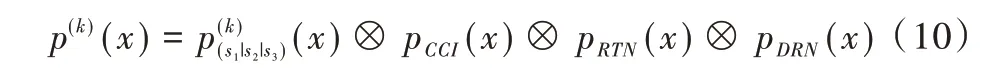
其中，Rl、Rr表示两个相邻的参考电压。MLC 闪存中，S1={00,01},S2={10,00} 。

令式（7）的概率比系数Q=600，根据式（7）、式（9）和式（10）得到的参考电压和重叠区域边界电压结果如表2 所示。

Table 2 Voltage after interference表2 发生干扰后的电压

根据上文非均匀感知法基本理论，它在一个重叠区域至少需要3 个数值，即两侧的感知电压与中间的硬判决感知电压，因此对于MLC 闪存，一共有3 个主要重叠区域。由此至少可以得到9 个感知电压值，具体的9 级非均匀存储感知电压如表3 所示。

Table 3 Class 9 non-uniform storage perceived voltage表3 9 级非均匀存储感知电压

根据式（8）可以得出，当S1=0 时，对应的第1 个比特为0 的LLR 值计算公式如式（11）所示。

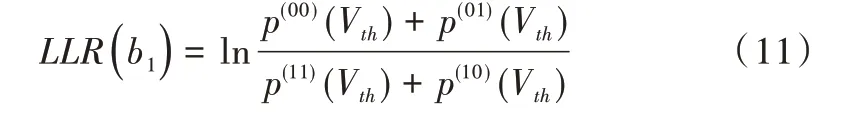
根据式（8）可以得出，当S2=0 时，对应的第2 个比特为0 的LLR 值计算公式为如式（12）所示。

在得到感知电压的的基础上，假设某一个存储单元的阈值电压Vth在感知电压区间(Rl,Rr]，一般设定阈值电压Vth如式（13）所示。

其中，Rl、Rr表示两个相邻的参考电压。

但是考虑到落在非重叠区域的电压值探测精度较低，因此本文不采用通过平均值计算阈值电压的方法计算LLR值，而是采用根据感知电压区间对闪存的各存储单元通过积分计算LLR 值，以提高在非重叠区域存储比特的LLR 计算准确度。

根据上文已经得到了感知电压区间(Rl,Rr]，因此根据式（11）—式（13）可以得到如表4 所示的位于(Rl,Rr]区间的阈值电压Vth对应的LLR 值。

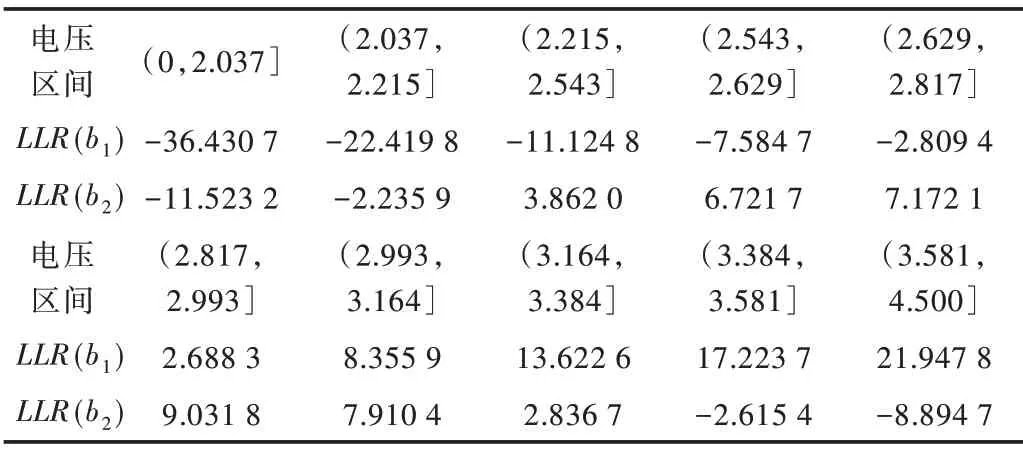
Table 4 LLR value corresponding to level 9 nonuniform perception in MLC NAND FLASH表4 MLC 闪存中9 级非均匀感知对应的LLR 值

由于非均匀存储感知中的存储感知等级数量越高，电压区间划分越细致，对电压的感知精度也越高，因此可以增大存储感知等级，使得LLR 的计算值更准确。

仅从表4 无法直接看出LLR 的分布规律，由于通过MLC 闪存信道的每一个存储比特对应一个LLR 值，意味着LLR 值受单个存储比特的影响，由此可以联想到互信息量。互信息I(X;Y)代表随机变量Y中包含随机变量X的信息量，或者说随机变量X由于已知随机变量Y而减少的不确定性。

因此，可以计算LLR 相对于存储比特的互信息量I(λ;X)。考虑到互信息量I(λ;X)在线性高斯模型中与最小均方误差（Minimum Mean Square Error，MMSE）的 关系［21］，可以将MLC 闪存信道和高斯信道联系起来，因此在高斯信道中根据互信息量I(λ;X)可得到LLR 的方差，再根据此方差构造新的极化码。

I(λ;X)的计算公式如式（14）所示。

其中，λ为存储信道中的LLR元素，p(λ|x=0) 和p(λ|x=1)的计算公式可通过式（15）推导得到。

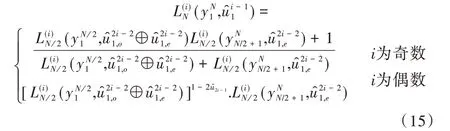
将L的部分看为一个整体，用exp（a）和exp（b）代替，并对式子左右都取对数，则式（15）转变为式（16）。

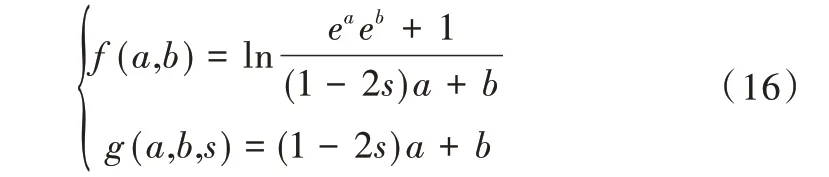
其中，a和b分别是信道1 和信道2 接收的对数似然比，s是根据概率运算后得到的信道1 的比特估计值。

将上述公式等效为式（17）。

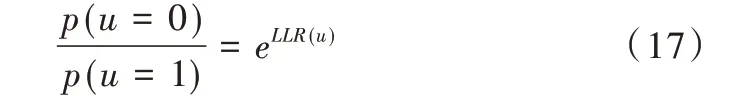
式（17）可以进一步等效为式（18）。

由此可以得出，p(λ|x=0)与p(λ|x=1)的计算公式如式（19）所示。

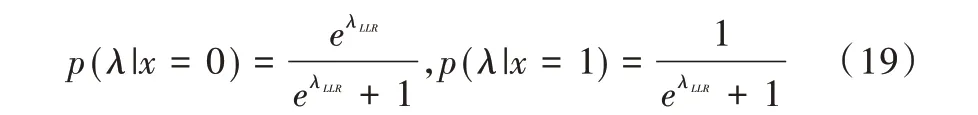
2.2 适用于闪存的优化巴氏参数凿孔极化码设计方法

由图7 中NAND FLASH 的纠错模型可知，若ECC 纠错码是极化码，则极化码应用于闪存的数据读写纠错系统的具体实施步骤为：首先通过闪存的Page 进行写入操作，在极化码编码器中输入源码信息序列；接着，在极化码编码器中进行编码操作，将写入的源码信息序列转化为编码序列；然后，经过格雷映射后从长度为N的比特序列变为长度为的比特序列对，随后将通过闪存的有噪传输信道并传输到极化码的译码器端口，译码器端口接收到的是受到闪存噪声源影响的存杵序列；最后，译码器端口接收到的通过译码后即可得到译码序列，从而完成对写入存储的数据读出的过程。

本文采用计算巴氏参数值的方法对信息位进行选取。由于MLC 闪存信道属于非BEC，文献［22］提出在非BEC 情况下对巴氏参数的计算方法，其中迭代计算单元位的巴氏参数时所需要的迭代初值可以表示为如式（20）所示。

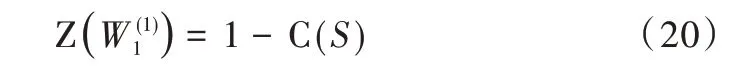
式（21）通过Ungerboeck 星座子集划分方法［23］计算单元位的容量。

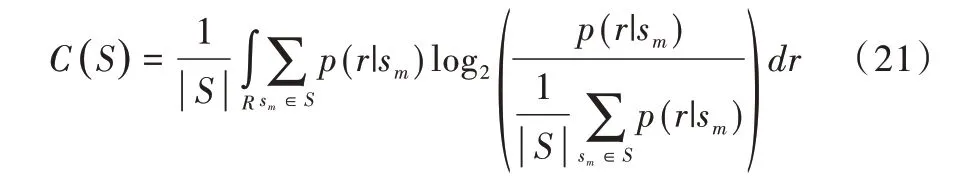
其中，C(S)表示存储单元位的容量。在闪存存储单元中，概率密度函数p(r|sm)服从的高斯分布，|S|表示存储单元状态的个数。最后，使用(N,K,R)定义极化码，可以在MLC 闪存中根据计算得到的巴氏参数初值构造极化码。

接下来，可以通过迭代计算存储单元位的巴氏参数进行极化码编码优化。巴氏参数是测量每个极化存储单元位可靠性的重要标准，如式（22）所示。

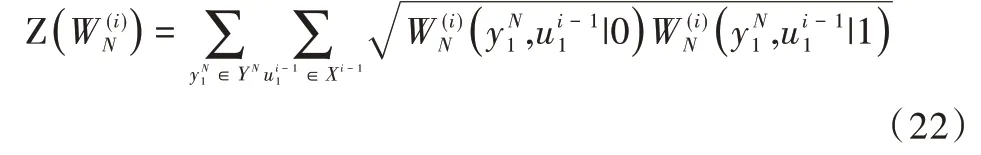
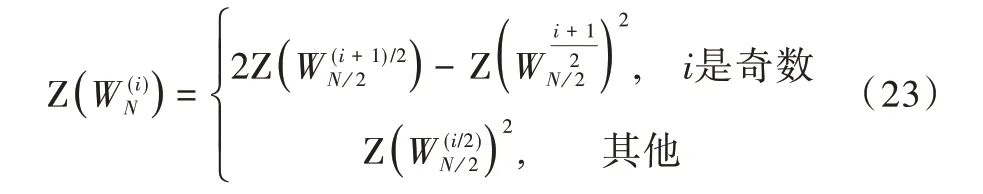
由此完成了对极化码码字的初步构造。MLC 闪存对码率的要求较高，且原始的码字不能满足其要求，因而采用了凿孔的方法，使得极化码构造高码率的码字，并将其应用于MLC 闪存中进行纠错。凿孔极化码的具体过程如图9 所示。

Fig.9 Encoding and decoding process of pubctured polar code图9 凿孔极化码编译码过程

凿孔比特一般选取可靠性较小的比特进行凿孔，这样得到的码字能最大程度地还原原码字的性能。因此，将巴氏参数值按降序排序，在凿孔时选择凿孔排序在最前面的索引，这些比特位的巴氏参数值最大最不可靠。首先构造码字(N,K)，设P是凿孔比特的个数，上介绍了迭代计算每个信道的，由于对信息比特凿孔会使得极化码性能大幅度降低，本文默认先凿冻结比特，其对应凿孔比特信道的巴氏参数大小满足式（24）。

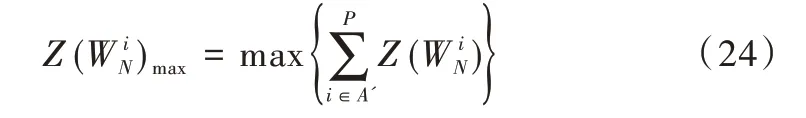
其中，A′表示冻结比特的信道索引集合，P为凿孔比特个数。

闪存中存储的数据不仅包括外界写入的存储数据，也有自己内部的一些数据。其中，存储固件所用的临时数据和信息通常被称为元数据。将这些元数据传送到极化码中，由于闪存对此已知，可以将其放在信息序列中不大可靠的位置，当需要对极化码凿孔时，可以根据需要将其凿去，由于译码端已知其信息，在译码时可以不设置为0。

将优化巴氏参数法和凿孔法结合，构造出的新码字可以更好地适应闪存高码率的要求，也可更好地对闪存进行纠错，其编译码流程如图10 所示。根据上文得到的LLR 拟合方差计算出存储单元容量，并利用优化巴氏参数法将极化码码字进行重新构造，通过极化码编码得到码字(N,K)，其中有H 比特闪存已知的元数据信息。再根据凿孔法进行码率匹配，选取巴氏参数值最大即信道可靠度最低的比特进行凿孔，待构造的凿孔码字为(N1,K)，凿孔数为P(P=N-N1)，构造高码率的极化码码字。此时，将码字写入MLC 闪存页中，由于MLC 闪存拥有大容量的存储空间，因此可以将信息比特和冻结比特分开存储，将前者存储到数据区，后者存储到数据冗余区，这样可以更好地利用闪存空间。在经过闪存的各种噪声干扰后，将其输入到译码器输入端，并在此时凿孔码字的对应位置插入P个对应比特信息，按巴氏参数值降序排列，前P-H 个插入为0 比特，后H 个插入对应的元数据信息，得到待译码码字。使用对应的译码算法，最后得到估计结果，再得到对应的信息序列。

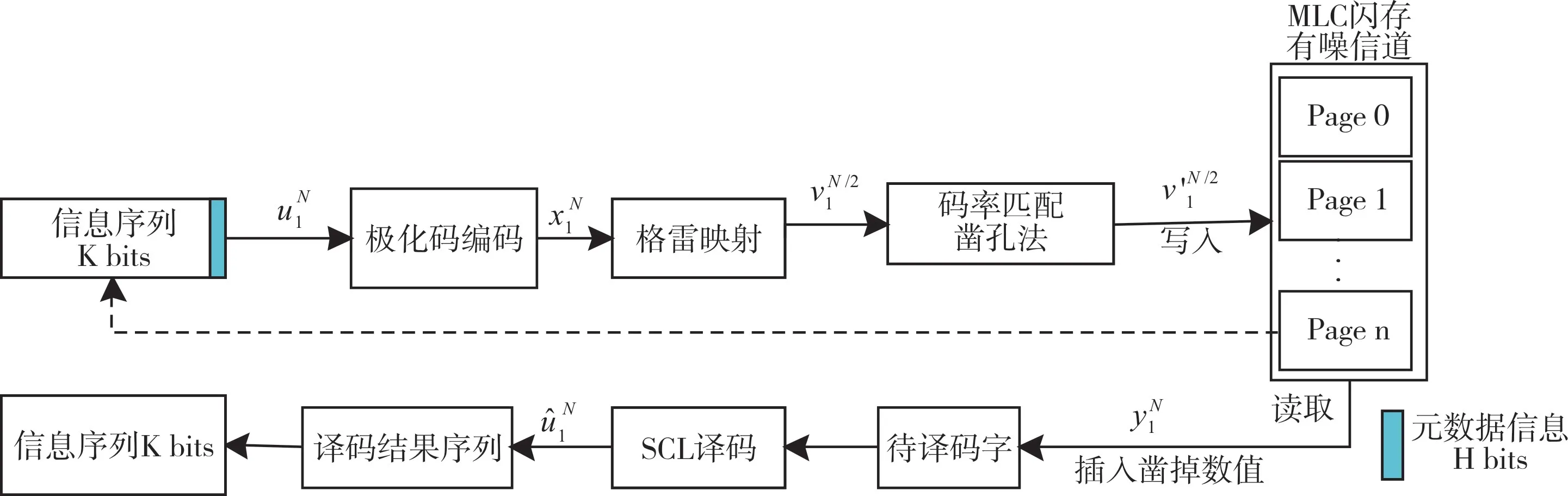
Fig.10 Polar code error control process of MLC NAND FLASH图10 极化码对MLC 闪存差错控制过程

3 系统仿真与分析

3.1 极化码编译码方法对闪存纠错性能的影响

首先对适用于MLC 闪存的不同编码方式构造的极化码进行仿真。闪存的特点之一是存储容量很大，因此闪存的块容量及其他内部区域容量也非常大。通常一块闪存芯片的总容量为（128G+9 728M）bits，每片包含2 048 块，在闪存块中1 块有512 页，而页中存在数据区和冗余区，前者有16kByte 容量的信息，后者有1 216Byte 容量的信息。若不经过加工而直接将闪存的页容量作为码长，则一共有（16k+1 216）Byte，若是直接对如此巨大容量的闪存进行纠错，则效率极低，计算机负荷也会很重。因此，本文采用3种不同的容量拆分方案，将每页拆分成几百段，则每段的编译码效率会提高很多，总体效率和可靠性也会随之提高［24］。3 种不同方案的凿孔极化码码字构造如表5 所示。

以方案一为例，具体拆分过程如下：首先将闪存每页分为1 024 段，每段分配128bits 的数据区和8bits 的冗余区。因此适用于闪存的极化码（N1，K）为（136，128），其中N1=136 为码字长度，K=128 为信息比特长度。（N1，K）是（N，K）经过凿孔操作后得到的码字，由于极化码的码长N=2n，因此构造的码字长度应为N=2n>136，为了提高效率，选择（N，K）为最接近的（256，128），可得出冻结比特中凿孔比特数目P=N-N1=120。

Table 5 Character construction of three punctured polar codes for MLC NAND FLASH表5 适用于MLC 闪存的3 种凿孔极化码码字构造

将不同构造方法得到的极化码应用于MLC 闪存中，进行仿真实验，并且将优化巴氏参数法与高斯近似构造法进行比较。并且，将这两种构造方法应用于3 种不同凿孔拆分方案的MLC 闪存中，得到6 种不同码字的凿孔极化码。在仿真实验中，采用SCL（L=4）译码方案。设定元数据信息H=16bits。

由于读取电压的改变，本文对SNR 的定义如式（25）所示。

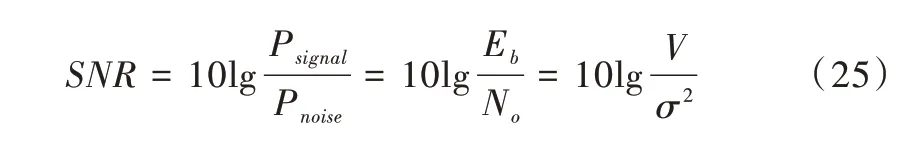
图11—图13 是优化巴氏参数法和传统的高斯近似法方法分别应用于凿孔方案一、二、三时的误比特率性能曲线。可以得到如下结论：利用优化巴氏参数法构造的凿孔码字相比高斯近似和蒙特卡洛法具有更好的误比特率性能。当BER=10-1时，构造（136，128）码字的优化巴氏参数法相比高斯近似和蒙特卡洛法获得的性能增益约为2.32和0.12dB；构造（272，256）码字的优化巴氏参数法相比高斯近似和蒙特卡洛法获得的性能增益约为2.1 和0.13dB；构造（550，512）码字的优化巴氏参数法相比高斯近似和蒙特卡洛法获得的性能增益约为1.7 和0.15dB。

Fig.11 Bit error rate diagram constructed by different encoding methods（136，128）图11 不同编码方法构造（136，128）误比特率

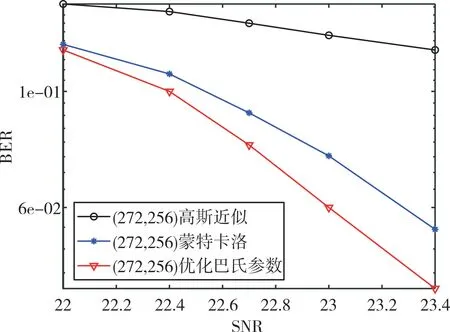
Fig.12 Bit error rate diagram constructed by different encoding methods（272，256）图12 不同编码方法构造（272，256）误比特率

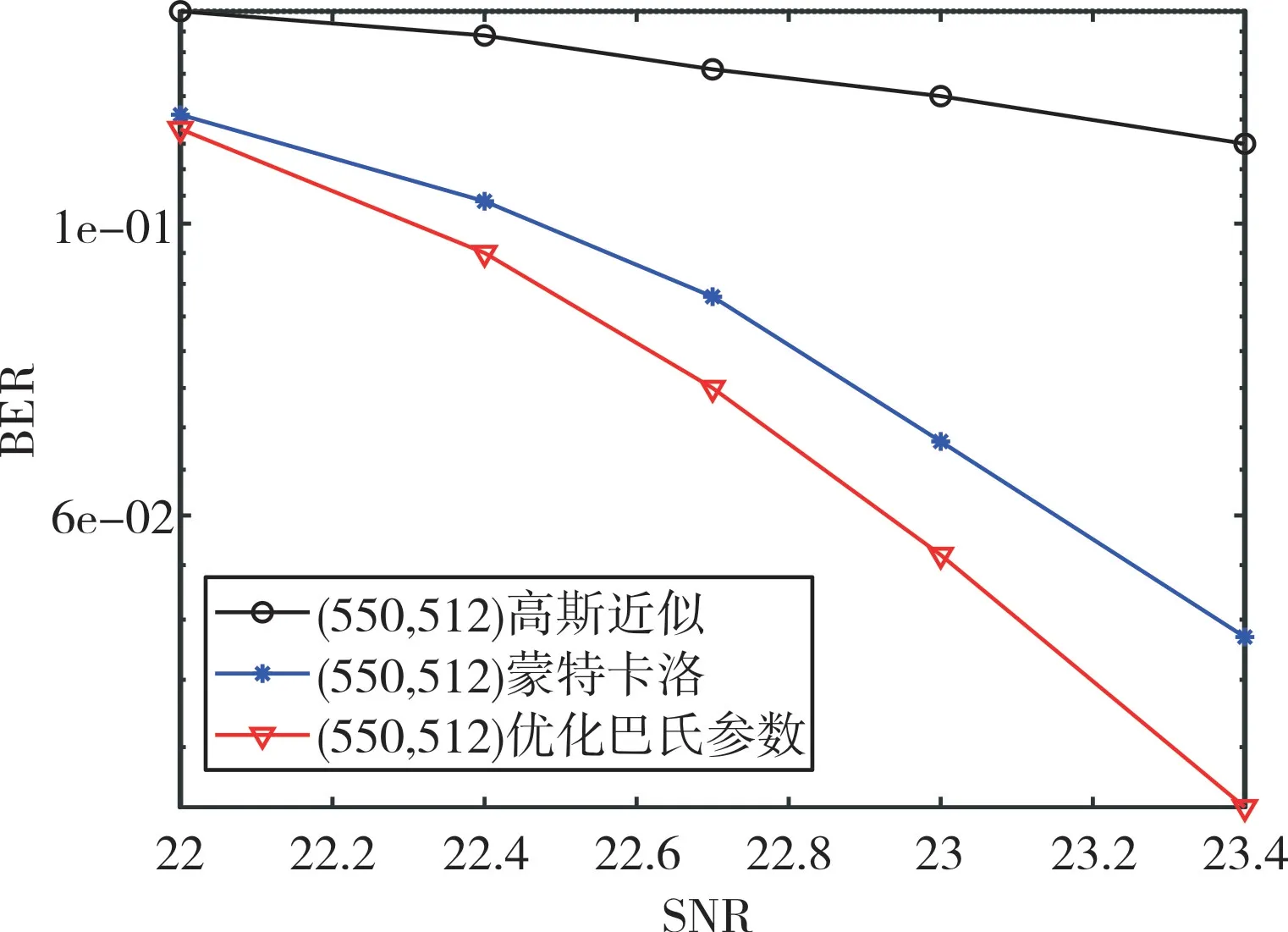
Fig.13 Bit error rate diagram constructed by different encoding methods（550，512）图13 不同编码方法构造（550，512）误比特率

从图11—图13 可知，使用优化巴氏参数构造法时，构造（550，512）码字的误比特率性能更好，原因在于随着码长的增加，极化码的性能会随之增强。因此，3 种凿孔码字中方案3 构造的（550，512）码字在闪存中具有更好的纠错性能。

由图14 可知，采用不同的译码方法，可以得到不同性能的仿真曲线。图14 所示的2 条曲线分别是SCL（L=1、4时）译码算法下得到的误比特率仿真图，采用优化巴氏参数编码方法构造（136，128）凿孔码字，当BER=10-1时，SCL（L=4）相比SCL（L=1）（即SC），可以得到约0.2dB 的性能增益。

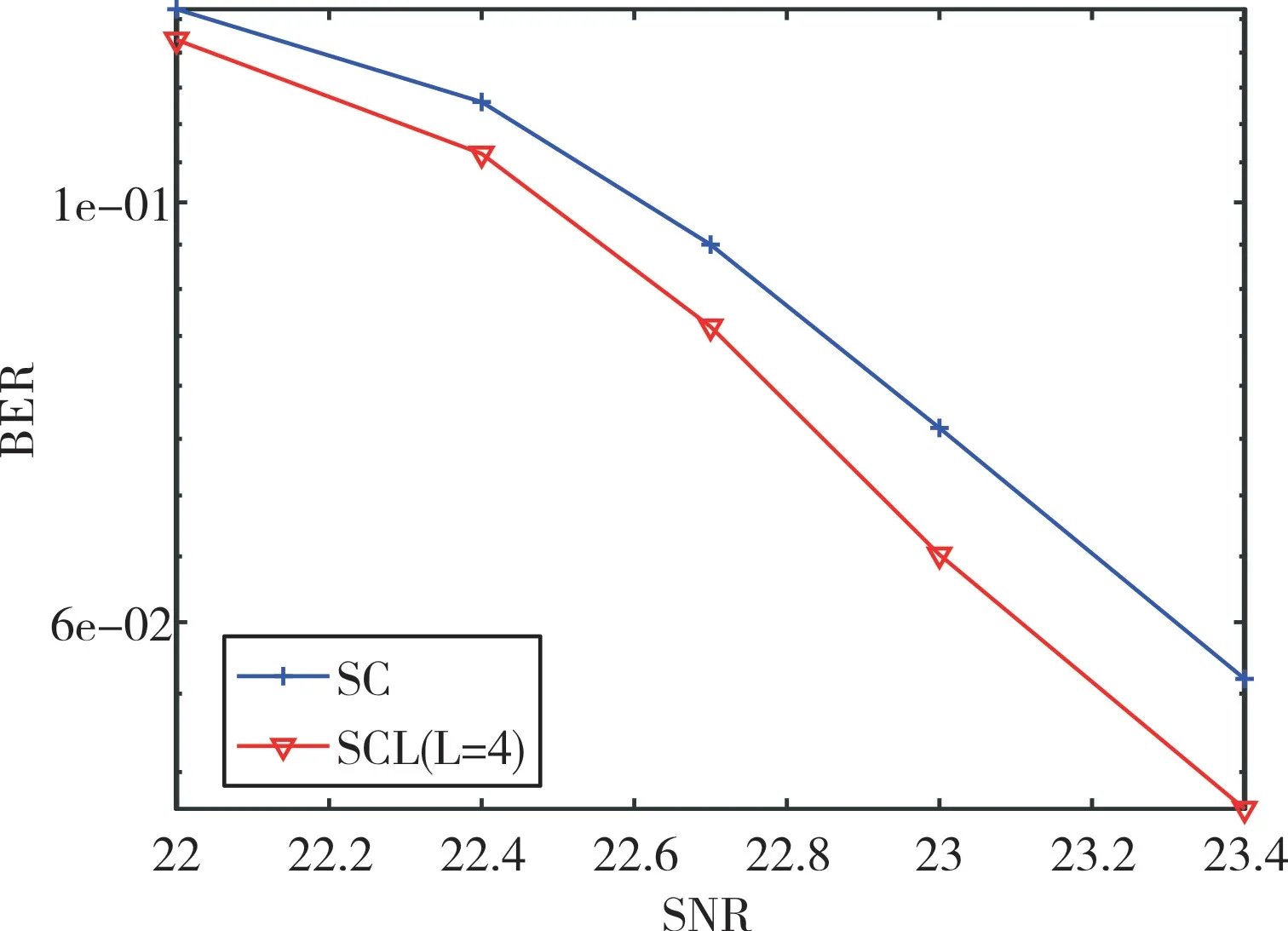
Fig.14 Bit error rate diagram constructed by different decoding methods（136，128）图14 不同译码方法构造（136，128）误比特率

3.2 阈值电压分布对闪存纠错性能的影响

由于阈值电压分布的改变会导致主要重叠区域大小的改变，而主要重叠区域的大小也会影响感知数据的精度。若是阈值电压分布的改变导致主要重叠区域变大，则对数据的感知精度要求更高；若是阈值电压分布的改变导致主要重叠区域变小，则会降低对数据的感知精度要求。因此阈值电压分布的改变会影响对数据的感知精度，也会影响读取闪存存储数据的可靠性。

鉴于优化巴氏参数构造法相比其他构造法具有更好的误比特率性能，使用优化巴氏参数法构造（136，128）凿孔码字，采用SCL（L=4）译码算法，观察当闪存中擦除单元的标准差改变时，极化码的误比特率性能变化，如图15 所示。

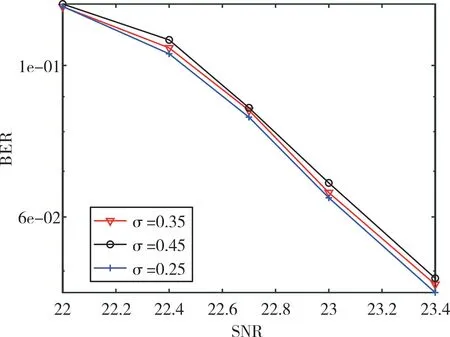
Fig.15 Bit error rate of NAND FLASH erasing unit with different standard deviation图15 闪存擦除单元标准差不同时的误比特率

图15 表示闪存擦除单元的标准差σ 不同时，（136，128）凿孔极化码的误比特率性能曲线。可以得到如下结论：当擦除状态阈值电压的标准差变小时，极化码的误比特率性能有一定提升。当BER=10-1时，与σ=0.35、0.45 的曲线相比，σ=0.25 的曲线分别获得了约0.035 dB 与0.08 dB的增益。这是因为随着擦除状态标准差的不断减小，闪存单元之间的重叠区域也逐渐减小，存储感知精度上升，使得极化码的纠错性能得到提升。

4 结语

本文将闪存存储单元的LLR 值拟合为高斯分布，并将其方差与极化码构造相关联，使得极化码可以适用于闪存存储数据的纠错应用中，但是由于闪存通常要求较高的码率，故引入凿孔极化码解决码率兼容问题。根据闪存页容量和已知的元数据信息，拆分出不同的凿孔极化码，通过仿真结果可知，本文提出的优化巴氏参数法相比高斯近似和蒙特卡洛法的误比特率性能更好，并且优化巴氏参数法构造的（550，512）凿孔码字相比其他凿孔码字具有更好的纠错性能。当改变SCL 译码算法的L 值，闪存的误比特率性能会随着L 的增大而增强。本文还验证如下：随着闪存擦除单元标准差的减小，各存储单元之间的噪声干扰减弱，存储器对存储数据的感知精度上升，极化码的纠错性能提升。但同时也存在一些不足，如阈值电压分布状态的改变对极化码纠错的影响还没有研究透彻。本文主要分析了擦除状态阈值电压分布的改变对极化码纠错性能的影响，未来还可以分析其他编程状态阈值电压分布的改变对极化码纠错性能的影响。