数字信号处理课程中频率分辨率的教学探讨

张腾达 董敬涛 杨蕾 卢荣胜 张育中

摘  要：频率分辨率是数字信号处理课程中的一个重要概念，因为它对DFT参数的选择有着重要影响。在教学过程中，容易将频率分辨率和计算分辨率相混淆。文章首先介绍了频率分辨率和计算分辨率的基本概念，然后以含有等幅的两个单频的信号为例，对DFT何时能分辨两个等幅单频信号的谱峰和序列尾部补0的作用进行了详细分析，并对相应MATLAB仿真结果进行论证。

关键词：数字信号处理;频率分辨率;DFT;计算分辨率;MATLAB

中图分类号：G642       文献标志码：A          文章编号：2096-000X（2022）01-0087-05

Abstract： Frequency resolution is an important concept in the course of digital signal processing， because it has an important influence on the selection of DFT parameters. In the teaching process， it is easy to confuse frequency resolution with computational resolution. Here， the basic concepts of frequency resolution and computational resolution are firstly introduced. Then， a signal containing two single-frequency components with equal amplitude is used to demonstrate the way to distinguish the spectral peaks of the signal using DFT and the role of the supplemental zero at the end of the sequence of the signal. Finally， we verify the results using MATLAB simulation.

Keywords： digital signal processing; frequency resolution; DFT; computational resolution; MATLAB

用DFT（FFT）對模拟信号进行频谱分析是本科数字信号处理课程中的一个重点内容，而频率分辨率又是频谱分析中的一个难点，学生普遍对这部分内容理解不深入，对频率分辨率和计算分辨率这两个概念容易混淆。为此，笔者总结出讲解这部分内容的几个要点，可使学生更深入地掌握频率分辨率，并加深对DFT的理解，为DFT在工程实践中的正确应用打好基础。

一、频率分辨率和计算分辨率

频率分辨率是指所用的算法能将信号中两个靠得很近的谱峰保持分开的能力[1]。在实际应用中是指分辨两个不同频率信号的最小间隔。进行频谱分析最有效的方法通常是离散傅里叶变换（DFT）。DFT的实质是对序列频谱X（ejω）进行采样，其结果就是离散的数字域频谱X（k）。

对模拟信号进行采样得到序列，假设采样频率为fs，采样点数为N，采样间隔为Ts，数据记录长度为T0，进行DFT的点数为R，则频率分辨率F0为：

F0=1/T0=1/NTs=fs/N 。  （1）

要提高频率分辨率，在采样频率fs一定的情况下，只能增加采样点数N，但N太大会影响系统的处理速度;而采样点数N一定时，必须减少采样频率，在满足采样定理的条件下，这样会减少频谱分析的范围。由此看来，为了保证一定的频率分辨率，在进行频谱分析时，采样频率和采样点数要同时考虑。频率分辨率在有的文献上也被称为“物理分辨率”[2]，为了和物理分辨率相区别，把做DFT时所得到的最小频率间隔称为“计算分辨率”[2]，即该分辨率是靠计算得到的，但它并不能反映真实的频谱分辨能力，则计算分辨率F为：

F=fs/R。            （2）

一般情况下R？叟N。R=N时，频率分辨率等于计算分辨率;R>N时，相当于将N点的采样序列补0至R点，然后再计算R点的DFT，此时计算分辨率优于频率分辨率，达到改善频谱可视效果，因此计算分辨率有文献也称为“可视分辨率”[3]。

二、两个等幅单频信号谱峰的分辨

在用DFT（FFT）对模拟信号进行频谱分析时，假设对模拟信号进行采样得到的序列为x（n），对它用矩形窗进行截断，得到长度为N的采样序列：

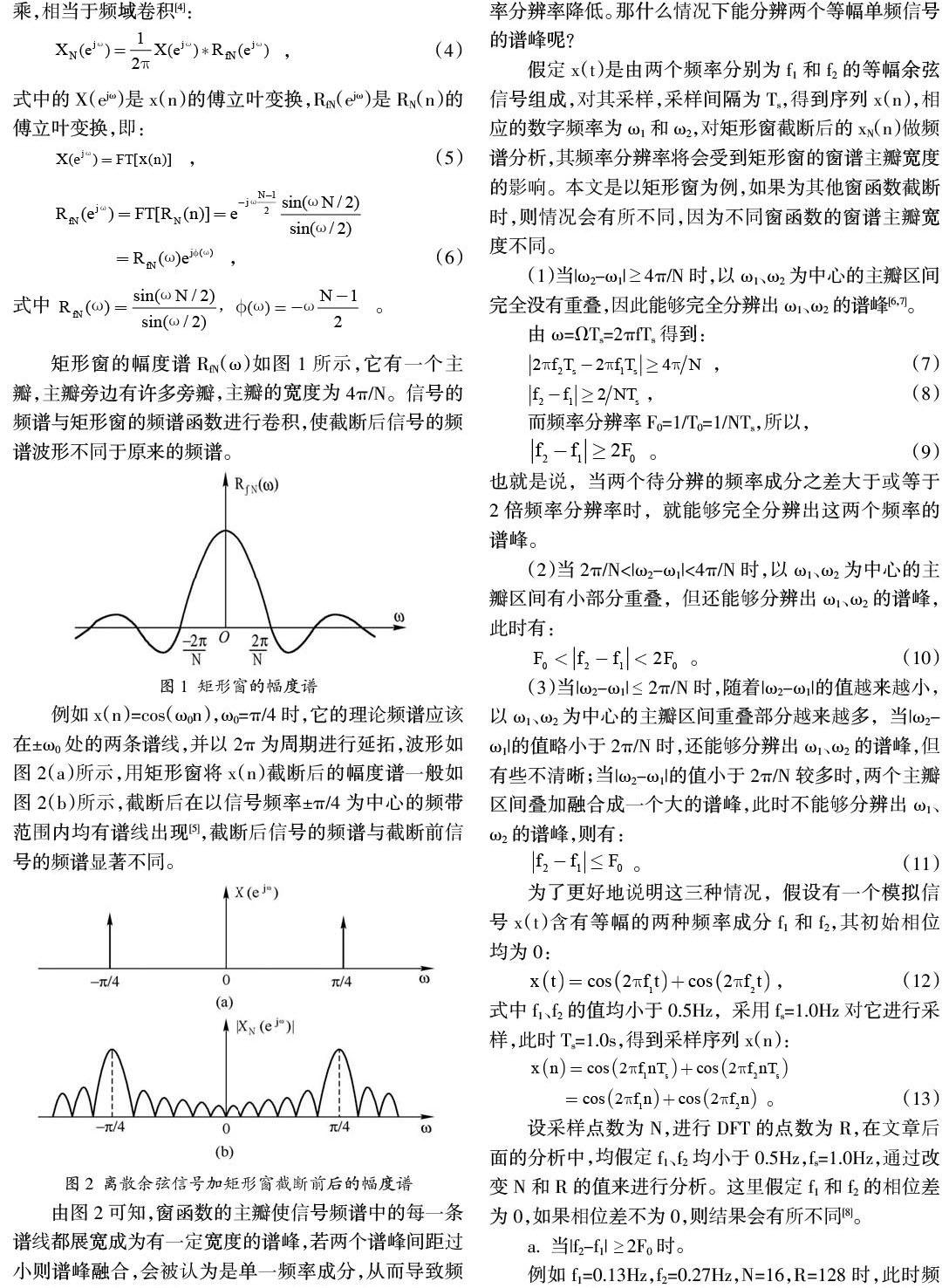
矩形窗的幅度谱RfN（ω）如图1所示，它有一个主瓣，主瓣旁边有许多旁瓣，主瓣的宽度为4π/N。信号的频谱与矩形窗的频谱函数进行卷积，使截断后信号的频谱波形不同于原来的频谱。

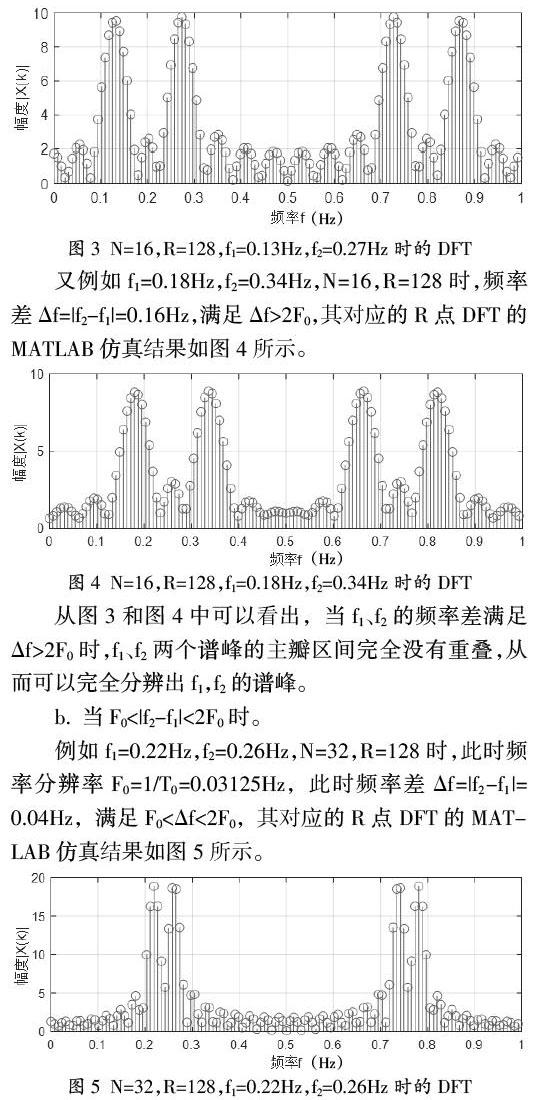
例如x（n）=cos（ω0n），ω0=π/4时，它的理论频谱应该在±ω0处的两条谱线，并以2π为周期进行延拓，波形如图2（a）所示，用矩形窗将x（n）截断后的幅度谱一般如图2（b）所示，截断后在以信号频率±π/4为中心的频带范围内均有谱线出现[5]，截断后信号的频谱与截断前信号的频谱显著不同。

由图2可知，窗函数的主瓣使信号频谱中的每一条谱线都展宽成为有一定宽度的谱峰，若两个谱峰间距过小则谱峰融合，会被认为是单一频率成分，从而导致频率分辨率降低。那什么情况下能分辨两个等幅单频信号的谱峰呢？

假定x（t）是由两个频率分别为f1和f2的等幅余弦信号组成，对其采样，采样间隔为Ts，得到序列x（n），相应的数字频率为ω1和ω2，对矩形窗截断后的xN（n）做频谱分析，其频率分辨率将会受到矩形窗的窗谱主瓣宽度的影响。本文是以矩形窗为例，如果为其他窗函数截断时，则情况会有所不同，因为不同窗函数的窗谱主瓣宽度不同。

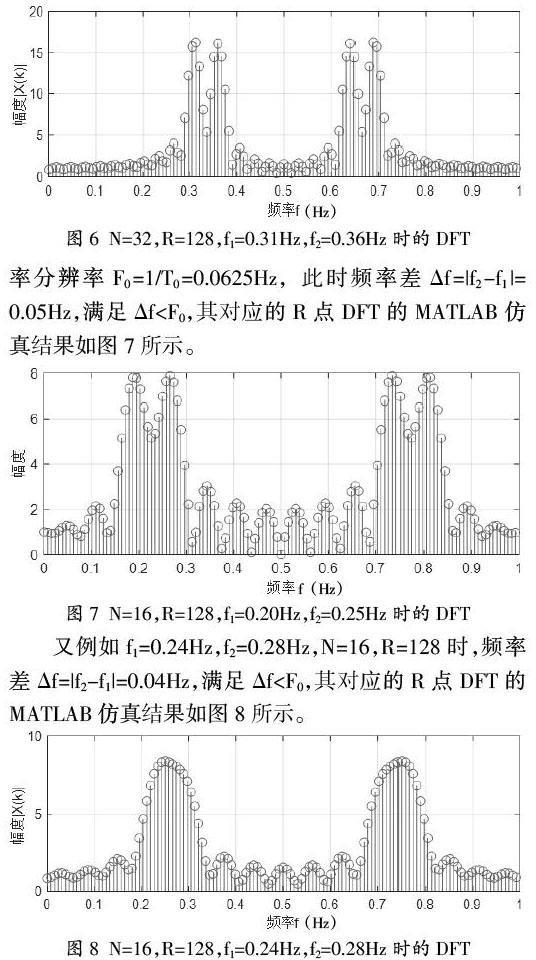
从图7中可以看出，当f1、f2的频率差？驻f略小于F0时，还能够分辨出f1、f2的谱峰，但有些不清晰;从图8中可以看出，当频率差？驻f小于F0较多时，f1、f2两个谱峰的主瓣区间叠加融合，形成一个大的谱峰，从而完全分辨不出f1、f2的谱峰。

三、序列尾部补0的作用

1. 序列尾部补0可以减小栅栏效应，提高计算分辨率，改善频谱的可视效果。

序列x（n）的R点DFT，其实际上是序列x（n）的DTFT X（ejω）在[0，2π]区间上的R点采样值，两个采样点之间的频谱值是不知道的，就好像被栅栏遮住一样，因此这种现象就被称为栅栏效应。为了减轻栅栏效应，可以通过增多DFT的变换点数R来实现。

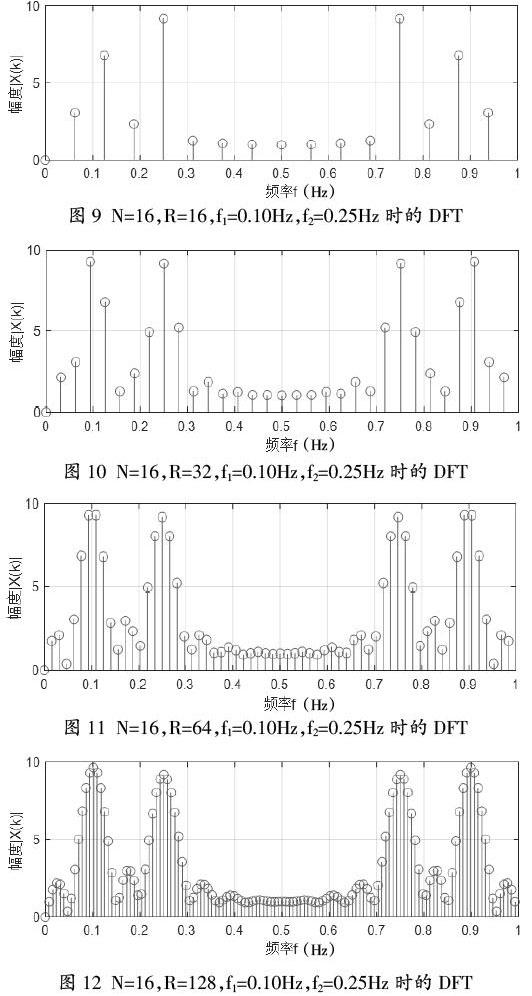
例如f1=0.10Hz，f2=0.25Hz，N=16时，则记录长度T0=N*Ts=16s，频率分辨率F0=1/T0=0.0625Hz，频率差？驻f=|f2- f1|=0.15Hz，此时？驻f>2F0=0.125，故能完全分辨出两个谱峰。

当R分别为16、32、64和128时，其对应频谱的MATLAB仿真结果如图9至图12所示。

图9中R=16，其计算分辨率为fs/R=0.0625，从图9可以看出，两个谱峰f1和f2虽然能够分辨出来，但可视效果不好。随着R的逐渐增大，计算分辨率越来越高，可视效果越来越好，即从图10到图12就能越來越清楚地分辨出f1和f2的两个谱峰。

2. 序列尾部补0不能提高频率分辨率，提高频率分辨率必须增加数据的记录长度。

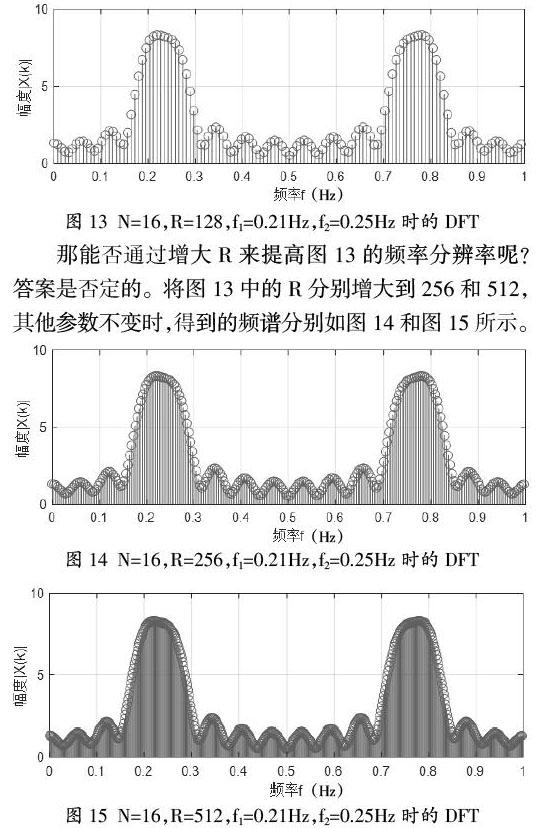
例如f1=0.21Hz，f2=0.25Hz时，取N=16，R=128，频率分辨率F0=0.0625Hz，频率差？驻f=|f2-f1|=0.04Hz，此时？驻f<F0，其对应频谱的MATLAB仿真结果如图13所示，显然从图中完全不能分辨出f1、f2的两个谱峰。

那能否通过增大R来提高图13的频率分辨率呢？答案是否定的。将图13中的R分别增大到256和512，其他参数不变时，得到的频谱分别如图14和图15所示。

从图14和图15中可以看出，R增大后，增加了频谱采样密度，提高了计算分辨率，但依然不能分辨出f1和f2的两个谱峰，即并没有提高频率分辨率。这是因为决定实际频率分辨率的是采样后序列x（n）的DTFT，即DFT的频谱包络，不同的频谱包络代表不同的频率分辨率，频谱包络不变就意味着频率分辨率不变，图13、图14和图15中的频谱包络并没有变化，就表明这三种情况下实际的频率分辨率并没变化。

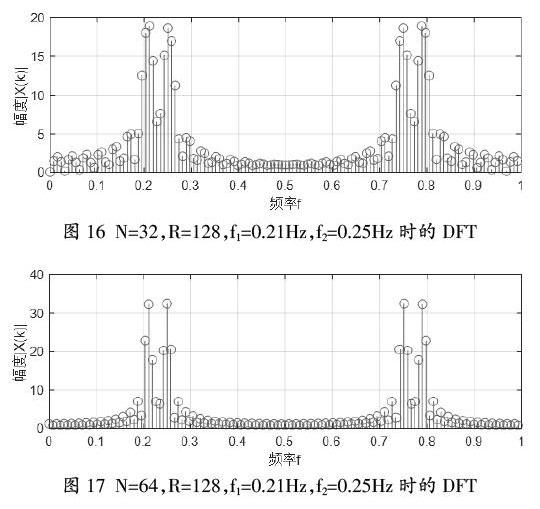
要提高频率分辨率，只能增加实际序列的记录长度。在采样频率fs不变时，即采样间隔Ts不变，要增加实际序列的记录长度，就必须增加采样点数N，因为T0=N*Ts。将图13中的N分别增大到32和64，其他参数不变时，得到的频谱的MATLAB仿真结果分别如图16和图17所示。

在图16中，频率差？驻f=0.04Hz不变，这时N=32，其频率分辨率F0=1/T0=1/32=0.03125Hz，此时F0<？驻f<2F0，故能分辨出两个谱峰f1和f2，但两个谱峰有部分重叠。

在图17中，频率差？驻f=0.04Hz依然不变。这时N=64，其频率分辨率F0=1/T0=1/64=0.015625Hz，显然有？驻f>2F0，故能完全分辨出两个谱峰f1和f2。

3. 序列尾部补0可使数据R为2的整数次幂，以便于使用快速傅里叶变换算法（FFT）。

四、结束语

用DFT（FFT）对模拟信号进行频谱分析时， 频率分辨率只与序列的记录长度成反比，因此，要提高频率分辨率，只能增加实际序列的记录长度，而不能通过序列尾部补0来实现，但序列尾部补0可以减小栅栏效应，提高计算分辨率，改善频谱的可视效果。

对含有两个等幅单频f1和f2的模拟信号进行时域采样，并以矩形窗截断时，利用DFT进行频谱分析，当f1和f2的频率差？驻f满足？驻f  2F0时，f1和f2两个谱峰的主瓣完全没有重叠，可以完全分辨出f1和f2的谱峰;当F0<？驻f<2F0时，f1和f2两个谱峰的主瓣区间有小部分重叠，但还是可以分辨出f1和f2的谱峰;当？驻f  F0时，情况比较复杂，当？驻f略小于F0时，还能够分辨出f1和f2的谱峰，但有些不清晰;当？驻f小于F0较多时，f1和f2两个谱峰的主瓣区间叠加融合成一个大的谱峰，从而完全分辨不出f1和f2的谱峰。

参考文献：

[1]胡广书.数字信号处理：理论、算法与实现（第三版）[M].北京：清华大学出版社，2012.

[2]Sophocles J O. Introduction to Signal Processing[M]. Prentice-Hall，1996;北京：清华大学出版社，1999（影印）.

[3]赵彦斌，张永瑞.信号谱分析中参数选择对频率分辨率的影响[J].电子科技，2005（11）：8-11.

[4]程佩青.数字信号处理教程（第四版）[M].北京：清华大学出版社，2013.

[5]高西全，丁玉美，阔永红.数字信号处理——原理、实现及应用（第2版）[M].北京：电子工业出版社，2010.

[6]张小虹.信号截短对频谱分辨率的影响[J].电气电子教学学报，2005（1）：21-24+94.

[7]刘密歌.频率分辨率的研究[J].电子测量技术，2020，43（6）：165-168.

[8]王刚，王艳芬，张晓光，等.关于离散傅里叶变换频率分辨率的讨论[J].电气电子教学学报，2006（6）：18-20+24.