非结构混合网格在气动热标模模拟中的应用

张培红， 张耀冰， 赵 炜， 周桂宇， 吴晓军， 杨福军

(中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000)

1 引 言

非结构网格方法消除了网格节点的结构性限制，易于控制网格单元的大小、形状及网格点的位置，比结构网格具有更大的灵活性，对复杂外形的适应能力非常强，是最近十多年发展最快的一种CFD技术[1,2]。以AIAA阻力会议为例，第一届会议18个程序中有7个为非结构程序，第二届会议30个结果中非结构程序有11个，第三届会议26个参加者中有11个使用非结构程序，第四届会议提交的28个结果中非结构网格的计算结果达到了17个[3-7]。美国NASA的USM3Dns，NSU3D和FUN3D、美国空军的Cobalt60、波音公司的BCFD、欧洲DLR的TAU、FOI的EDGE以及日本JAXA的TAS等著名CFD软件都是基于非结构网格[8-10]；商业的非结构网格软件也非常多，如Metacomp Technologies公司的CFD++、ANSYS公司的CFX和Fluent以及CFDRC公司的CFD -FASTRAN等；还有许多开源软件也是非结构网格代码，如OpenFlower和OpenFoam等[11]。

但是，由于非结构网格在黏性区域很难使用类似结构网格的大长宽比网格，导致黏性预测精度降低，严重阻碍非结构网格的应用和发展[12-14]。近年来，CFD工作者针对非结构网格的特点开展了大量的网格生成、梯度求解和计算格式等研究，特别是非结构混合网格生成和求解技术的发展，解决了非结构网格气动特性预测精度低的缺陷，促进了非结构网格在飞行器气动特性预测模拟中的应用[15-20]。非结构混合网格一般由四面体、六面体、三棱柱或者金字塔组成，本文在生成混合网格时，在物面粘性作用区生成大伸展比三棱柱形和金字塔形网格；在其他流动区域采用阵面推进方法生成四面体网格。但对于高超声速气动热流计算，由于高超声速流动中含有激波等强间断，流体黏性起主导作用，物理黏性摩擦决定了热流的大小，对黏性计算精度提出了更高的要求，在计算中受到物理模型、数值格式、网格分布、收敛过程以及热流后处理方法等诸多因素的影响和制约[21-24]。即使是CFD方法能够给出较为精确的气动力结果，对于壁面热流的预测往往也可能会有数量级的差异。高超声速气动热的数值模拟一直是CFD研究的难点和热点问题，尤其是采用非结构网格计算热流，还存在较大的困难，很难达到和结构网格相当的计算精度。主要有两个原因，一是非结构四面体网格单元无法保证对称性；二是四面体网格至少有一个面是和激波斜交，无法保证网格与激波正交，影响激波捕捉精度。

针对非结构四面体网格在计算热流时的缺陷，Gnoffo[25]发展了多维通量重构方法，通过改进通量重构方法，减少四面体网格的影响，在六面体剖分的纯四面体网格上得到了较好的热流计算结果。McCloud[26]在网格自适应技术方面开展了相关研究，发展了鲁棒稳定的激波区域网格自适应技术，基于常规的混合网格在探测到的激波面附近重新生成三棱柱网格，其余区域使用四面体网格填充，较好地改善了非结构/混合网格上的热流计算结果。

近年来，国内在结构网格的热流计算方面开展了较多的研究工作，在非结构/混合网格的热流计算方法研究方面也取得了一定进展，但开展的工作相对较少。贺立新等[27]使用有限元/有限体积混合方法基于混合网格在双椭球上得到了较好的热流计算结果。李泽禹[28]基于非平衡气体在混合网格上就球头绕流算例进行了数值计算，发现很难得到光滑连续的分布结果。许和勇等[29]利用自适应网格技术开展了典型高超声速飞行器气动热环境的数值模拟。万云博[30]应用多维方法基于常规混合网格对包含钝锥、钝双锥和双椭球等多种外形进行了数值模拟，得到了与实验值吻合较好的热流计算结果。

相关研究表明[23,24]，网格分布是影响热流计算的重要因素之一。本文基于非结构混合网格，以典型钝锥标模外形的高超声速绕流为研究对象，验证了计算方法的计算精度和可靠性，开展了不同网格形式和第一层网格不同间距的影响研究，为采用非结构混合网格气动热计算时的网格生成形式和第一层间距等提供了参考建议和指导。

2 数值方法

本文计算采用国家数值风洞工程(NNW)项目团队自主开发的基于格心的非结构混合网格流场解算器FlowStar。该解算器支持任意形状的网格单元，针对非结构混合网格的特点，通过改进传统的Green-Gauss梯度求解方法和传统的Roe格式Harten-Yee熵修正方法，提出了一种新的节点型Green-Gauss梯度求解方法和Harten-Yee熵修正改进方法，大大提高了非结构混合网格粘性计算精度，软件经过了大量标准算例的考核验证，在航空航天领域得到了广泛的应用。

采用有限体积法对空间进行离散，未知变量位于网格单元的体心。控制方程为守恒形式的非定常可压缩N-S方程,

(1)

式中Ω为控制体的体积，∂Ω为控制体封闭面的面积，W为守恒变量，Fc为无粘通量，Fv为粘性通量。

本文主控方程对流项采用二阶迎风Roe通量差分裂格式进行离散，粘性项采用中心差分格式离散，并采用多重网格技术进行收敛加速。湍流模型采用SST两方程湍流模型，湍流控制方程空间离散采用一阶迎风格式。主控方程和湍流方程的时间迭代采用LU-SGS(Lower Upper-Symmetric Gauss -Seidel)方法 。

Roe通量差分分裂格式具有很高的分辨定态激波的能力，较其他的一些通量分裂格式(如Van Leer格式)，该格式的耗散较小。Roe格式在控制体单元面上的通量表达式为

(2)

式中Fc为无粘通量，W为守恒变量，ARoe为Roe平均矩阵。

Roe平均矩阵和左右状态差的乘积的求法为

|ARoe|I J(WJ-WI)=|ΔF1|+|ΔF2,3,4|+|ΔF5|

(3)

为提高流场计算效率，采用了基于MPI的大规模并行计算技术、多重网格方法、低速预处理技术和当地时间步方法等加速收敛技术。

3 计算模型及网格

钝锥标模外形高超声速绕流是典型的高超声速三维粘性流动。图1为钝锥标模的几何尺寸示意图，图2为钝锥标模三维计算模型。钝锥球头半径为R=27.94 mm，半锥角为15°，长度L=447.04 mm。计算来流条件为Ma=10.6，Re=3.973×106/m，T∞=47.3 K，Tw=294.44 K，分别计算了0°和20°两个工况。

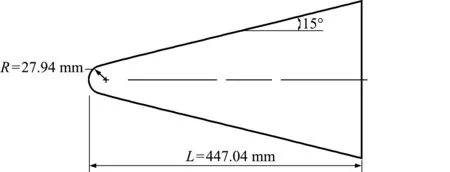
图1 钝锥几何尺寸

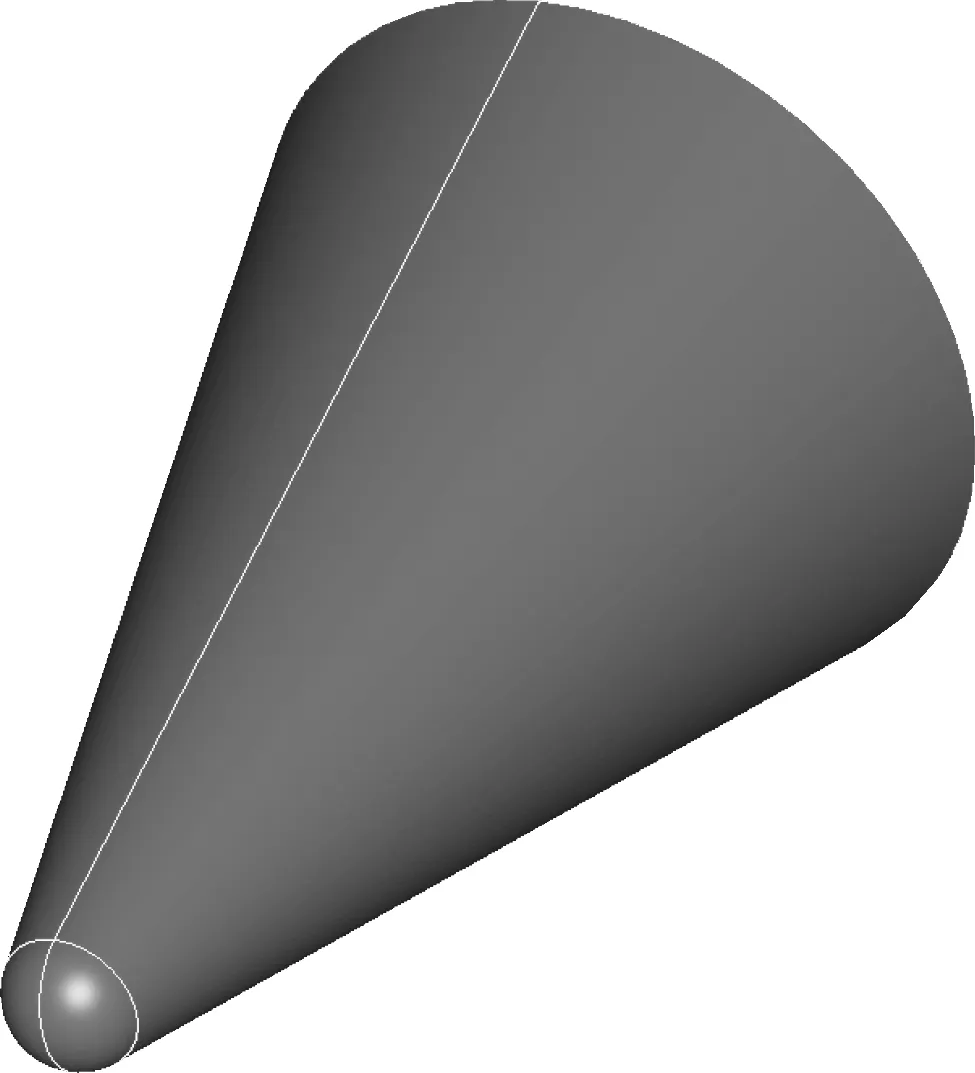
图2 钝锥计算模型

本文采用的非结构混合网格，均是以生成的一套结构网格grid-str为基础，通过剖分得到。结构网格grid-str第一层间距5×10-6m，网格雷诺数约为20，网格量约为196.6万个单元，其中周向点数257个，法向点数81个。图3给出了结构网格grid-str钝锥锥段和头部表面网格。

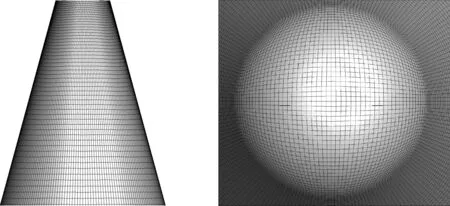
图3 钝锥锥段和头部表面网格(grid-str)

4 网格生成形式影响

为研究网格生成形式的影响，采用roe格式，对不同形式网格进行了计算研究。在结构网格grid-str的基础上，通过对头部网格采用不同剖分方式，共生成了7套非结构混合网格，分别为grid-unstr1，grid-unstr2，grid-unstr3，grid-unstr4，grid-unstr5，grid-unstr6和grid-unstr7，保持第一层网格间距5×10-6m不变，即保持网格雷诺数20不变。其中，grid-unstr1，grid-unstr2，grid-unstr3，grid-unstr4，grid-unstr5和grid-unstr6的头部网格在grid-str基础上采用不同方式剖分，尾部网格采用Advancing Front剖分直接生成非结构网格；grid-unstr7的头部网格与grid-unstr6完全相同，尾部网格是在grid-str基础上每个网格剖分成4个三角形单元。

grid-unstr1，grid-unstr2和grid-unstr3三套网格的头部网格是在grid-str基础上把每个四边形网格单元剖分为2个三角形单元，尾部采用 Advancing Front剖分直接生成非结构网格，不同在于三套网格头部采用的剖分方式，grid-unstr1采用绕圈剖分，grid-unstr2采用交叉剖分，grid-unstr3 采用放射剖分。grid-unstr1网格量为4125951个单元，grid-unstr2和grid-unstr3的网格量与grid-unstr1相近。图4给出了三种剖分方式得到的头部中心附近网格比较。

grid-unstr4采用Delaunay剖分方式，网格分布具有明显的任意性，grid-unstr5采用Advancing Front剖分方式，除头部中心附近外，网格具有较好的排列。grid-unstr4和grid-unstr5的尾部也均采用Advancing Front剖分直接生成非结构网格。

图4 不同剖分方式头部中心附近网格比较

grid-unstr6与grid-unstr2一样，头部网格是在grid-str网格的基础上采用交叉剖分方式生成，不同在于每个网格剖分成4个三角形单元，相比grid-unstr2网格量增加一倍。同样，grid-unstr6尾部也采用Advancing Front剖分直接生成非结构网格。grid-unstr7的头部网格与grid-unstr6完全相同，不同在于尾部网格也是在结构网格grid-str的基础上把每个网格剖分成4个三角形单元生成。图5给出了grid-unstr1和grid-unstr7锥段表面网格分布的比较。图6给出了grid-unstr1，grid-unstr2，grid-unstr3，grid-unstr4，grid-unstr5，grid-unstr6和grid-unstr7不同剖分方式头部网格比较。

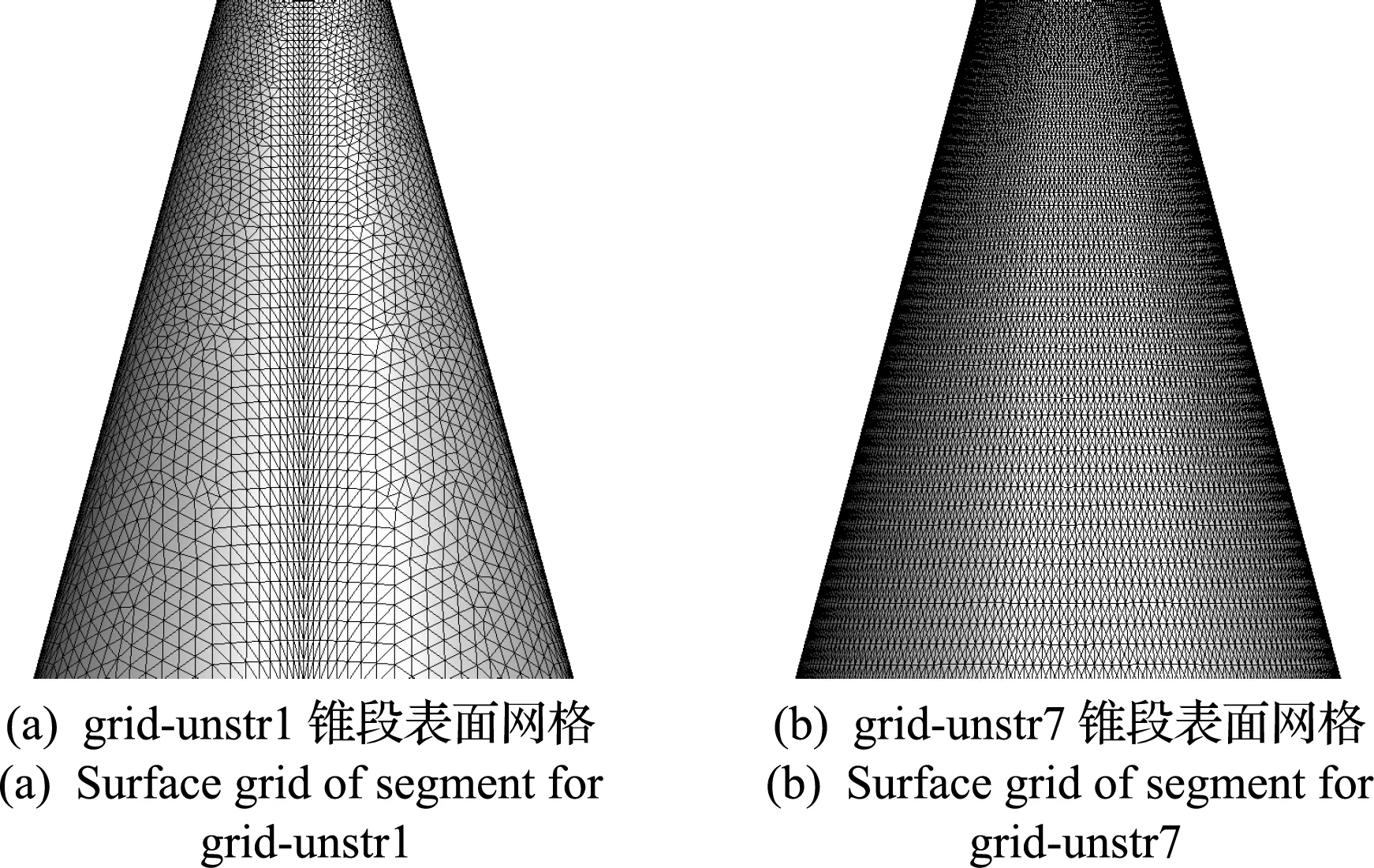
图5 grid-unstr1和grid-unstr7锥段表面网格分布比较

图6 头部网格分布比较

图7为Ma=10.6，α=0°时，不同网格头部壁面的热流分布。可以看出，不同网格头部驻点附近壁面热流分布有明显的差异，相对来说，grid-unstr1，grid-unstr2，grid-unstr6和grid-unstr7四套网格计算得到的壁面热流周向分布最好，但grid-unstr1 和grid-unstr2两套网格计算得到的驻点处热流值不是最大，明显不合理，grid-unstr6和grid-unstr7两套网格计算得到的壁面热流分布最好，两者基本上完全相同。

图8给出了Ma=10.6，α=20° 时，不同网格头部壁面热流不同剖面分布与实验比较。计算结果与试验值吻合较好，除六面体网格grid-str外，其他不同网格的计算结果相差很小。

图8 不同网格壁面热流与试验比较(Ma=10.6,α=20°)

综合不同网格计算得到的壁面热流云图分布和不同剖面壁面热流实验对比结果分析，要想较好地计算钝锥标模头部的热流分布，在研究的几种网格形式中，头部物面网格最好采用四边形或四边形交叉剖分得到的三角形网格，根据商业软件生成网格的便利性，推荐采用四边形交叉剖分得到的三角形网格。同时头部激波附近网格最好沿激波排列，激波靠近附面层的情况可以采用附面层三棱柱网格适当多向外推几层，激波远离附面层时可以采用baffle面的方式生成。

5 网格加密及第一层间距影响

为研究网格加密对计算结果的影响，在计算结果较好的网格grid-unstr6的基础上，将物面和空间网格尺度都加密一倍，得到grid-unstr8网格。图9给出了α=20° 时，网格加密前(grid-unstr6)和网格加密后(grid-unstr8)计算得到的壁面热流分布云图对比。图10给出了α=20°时，网格加密前(grid-unstr6)和网格加密后(grid-unstr8)计算得到的壁面热流分布比较。可以看出，与grid-unstr6相比，加密后网格grid-unstr8计算的壁面热流分布并没有明显的改进，说明针对目前的计算状态，已经无法通过网格加密明显改进计算结果。

图9 网格加密前后壁面热流分布云图对比(Ma=10.6,α=20°)

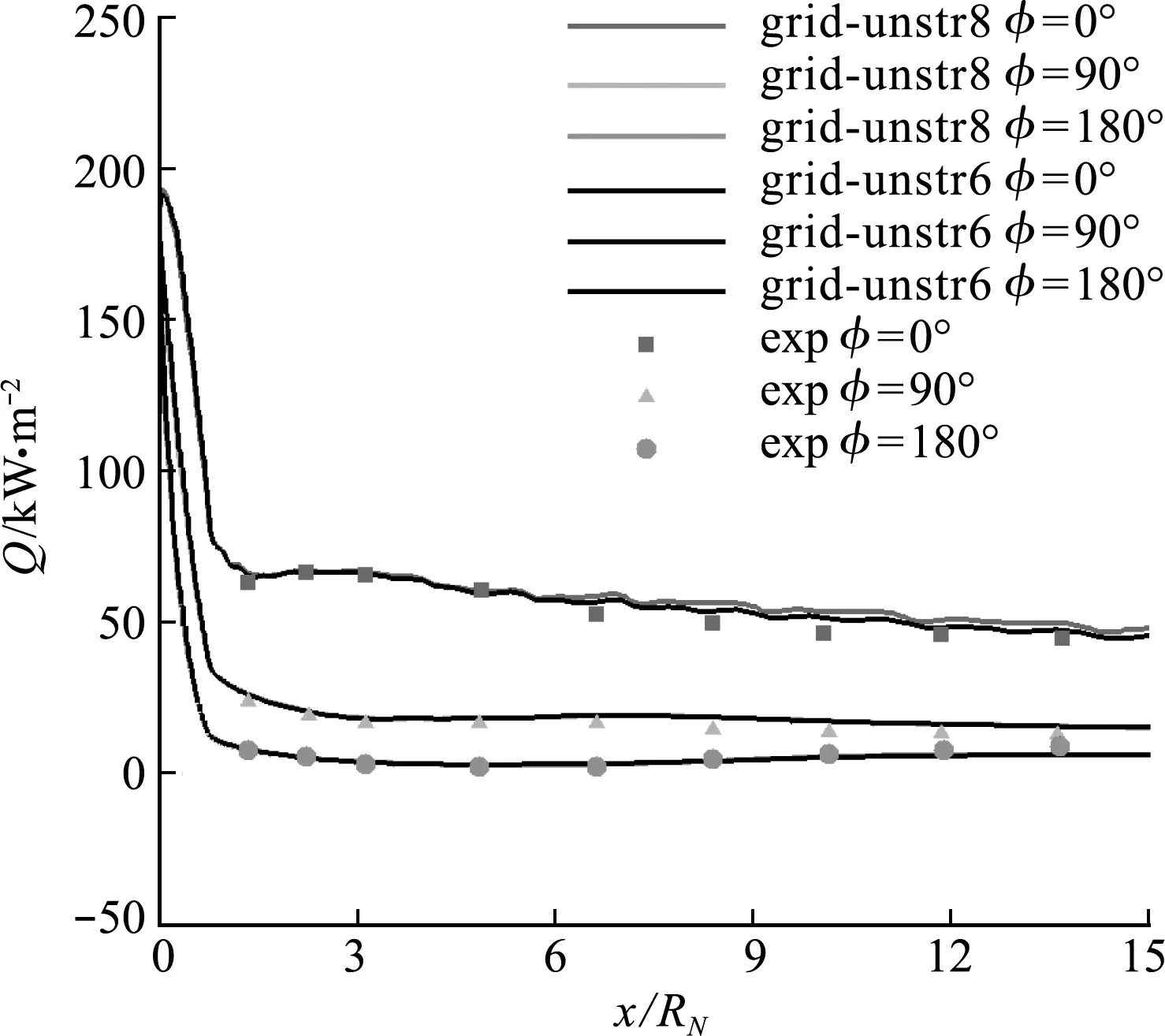
图10 网格加密前后不同位置壁面热流分布与试验比较(Ma=10.6,α=20°)

为进一步研究第一层网格间距的影响，在网格grid-unstr6的基础上，保持表面网格等其他参数不变，将法向第一层减小为五分之一，即第一层间距变为1×10-6m得到grid-unstr9，对应的网格雷诺数约为4；将法向第一层增大为五倍，即第一层间距变为2.5×10-5m得到grid-unstr10，对应的网格雷诺数约为100。

图11给出了α=20°时，不同第一层网格间距得到的壁面热流分布云图。图12给出了α=20° 时，不同第一层网格间距得到的壁面热流分布比较。三套网格得到的计算结果没有明显差别，相对来说，法向最密的grid-unstr9网格得到的驻点壁面热流分布轴对称性要好于其他两个，而第一层网格间距最大的grid-unstr10网格计算得到的壁面热流分布与物面网格明显相关。但是从计算收敛的角度，grid-unstr9由于网格太密，计算过程中会产生明显的网格刚性现象，残差下降异常慢，计算效率急剧下降。因此，法向间距不宜取得过密。

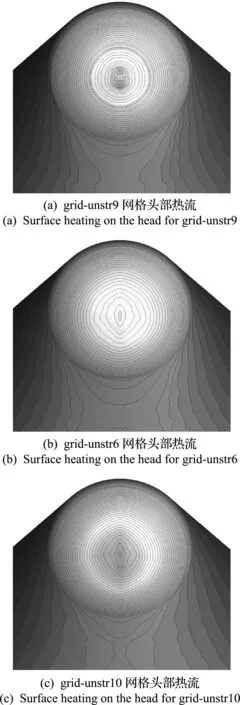
图11 网格第一层间距对头部壁面热流计算结果的影响(Ma=10.6,α=20°)

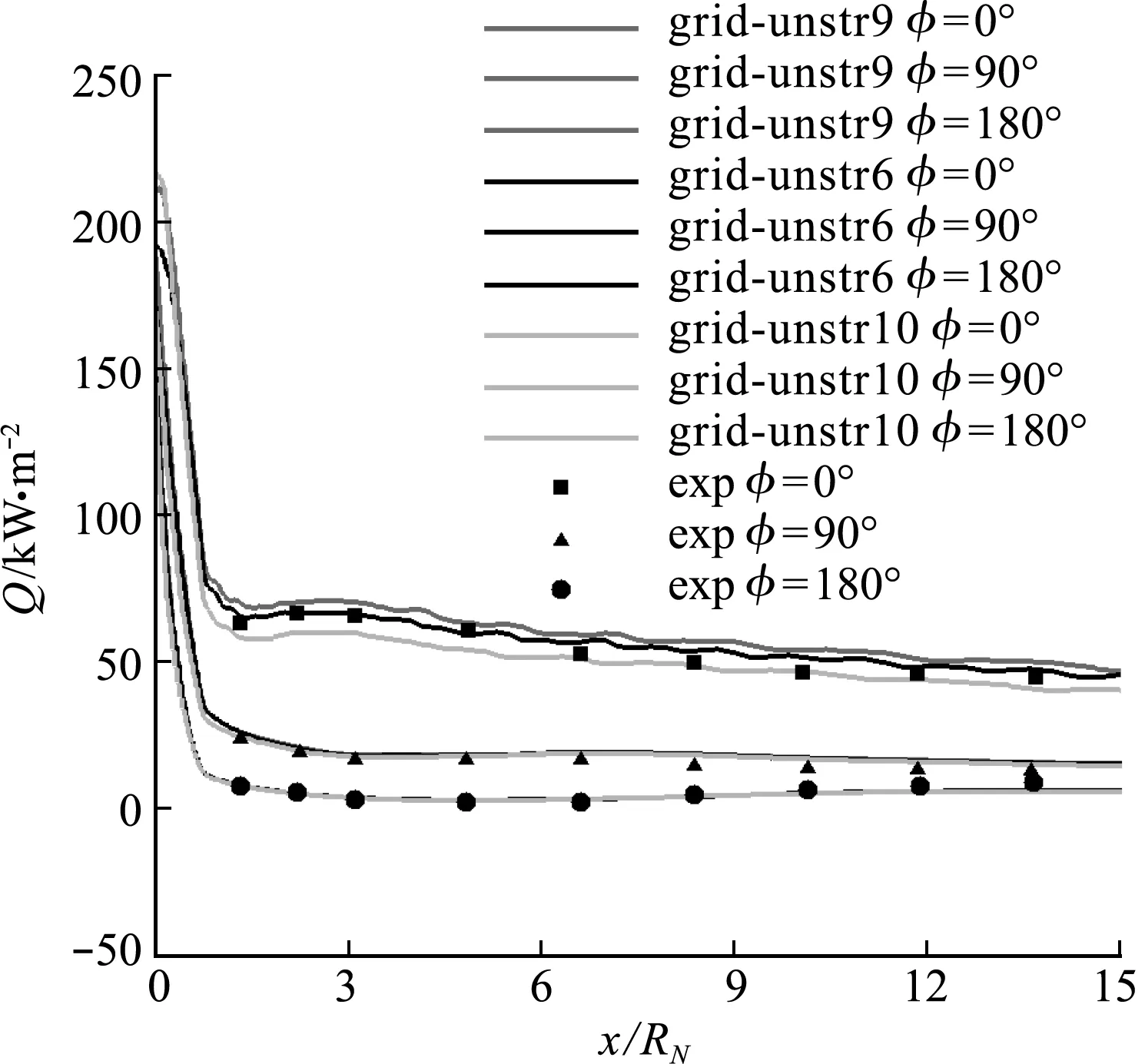
图12 网格第一层间距对不同位置壁面热流计算结果影响(Ma=10.6,α=20°)

6 结 论

本文以典型钝锥标模外形的高超声速绕流为研究对象，采用基于非结构混合网格建立的热流计算方法，开展了不同网格形式和第一层网格不同间距的影响研究，可以得到以下结论。

(1) 建立的热流计算方法，可以较好地模拟钝锥标模外形的高超声速绕流壁面热流分布。

(2) 热流计算时，头部物面网格最好采用四边形或四边形交叉剖分得到的三角形网格。

(3) 物面法向的网格雷诺数取20左右，过密的网格可能会产生网格刚性，降低计算效率。