基于多插值算法的大孔径井身结构三维成像探测装置设计探讨

汪发文， 徐 俊

(湖北省城市地质工程院，湖北 武汉 430050)

目前，各类地质钻孔和工程应用类钻孔的直径越来越大，而孔径超径或者缩径问题直接影响着工程下一步施工工序，对工程整体质量有着重要影响[1]，因此如何准确测量大口径钻孔孔径的难题亟待解决。一种现有测量技术方法是小口径钻孔孔径机械臂测量法[2]，主要为伞状测量，其主要缺陷有：①测量臂的伸展难题；②测量结果为数据或者孔身曲线，不能全方位展现钻孔孔身。另外一种现有测量技术方法是声波测量法[3]，其测量范围较大，但是声波需要依赖钻孔中的冲洗液作为媒介传播，受冲洗液性能影响非常大，其主要缺陷有：①冲洗液性能影响测量精度误差大;②对于漏失钻孔，冲洗液不能灌满钻孔，则上部无冲洗液孔段无法测量;③钻进过程中，钻孔孔壁会形成一定厚度的泥皮，声波测量则不能精准测量孔径尺寸，孔径整体偏小;④测量结果为数据或者孔身曲线，不能全方位直观展现钻孔孔身。因此现有的孔径测量设备不能准确测量大口径钻孔孔径。机械臂测量法主要针对小口径钻孔，测量臂伸展具有一定难度，仪器上行下放不易；声波测量法必须有传播媒介才能测量，并且声波不能穿透钻孔孔壁的泥皮，测量误差大，同时孔身测试显示为平面曲线，不能三维立体显示。

针对现有技术存在的问题，课题组设计出了一种能测量大口径钻孔孔径的方法，该方法通过接触式破除孔壁泥皮，能最真实地反映钻孔孔径，并采用一定技术手段，最终实现三维立体图像显示孔身，从而直观地了解钻孔缩径、扩径问题。这为更精准地计算固井用水泥浆提供了数据基础，同时也能直接检验护壁套管的变形磨损程度。本文主要阐述以大孔径井身结构三维成像测量方法及装置原理，同时根据测量原理，基于多种插值算法并依托Matlab软件进行程序设计编译与封装，最后采用随机生成井孔的数据对其方法的可行性与准确性进行验证。

1 技术方案原理与装置设计

本文所提出的大孔径井身结构三维成像的原理如图1所示。由图1可知，对于井孔的实际孔径，测量臂通过弹簧将其转化为压力数据，随后通过压电传感装置将压力数据转化为电学数据，测试装置测取该电学数据，并通过集成于内置微机中的逆向计算算法与柱面插值算法，得到井孔重构的内径轮廓。其中用于数据采集与处理的内置微机原理如图2所示。

1.1 数据转化与处理

利用井孔测试装置得到装置位于不同深度时的电流数据，将数据进行转换得到用于计算的各项长度数据。

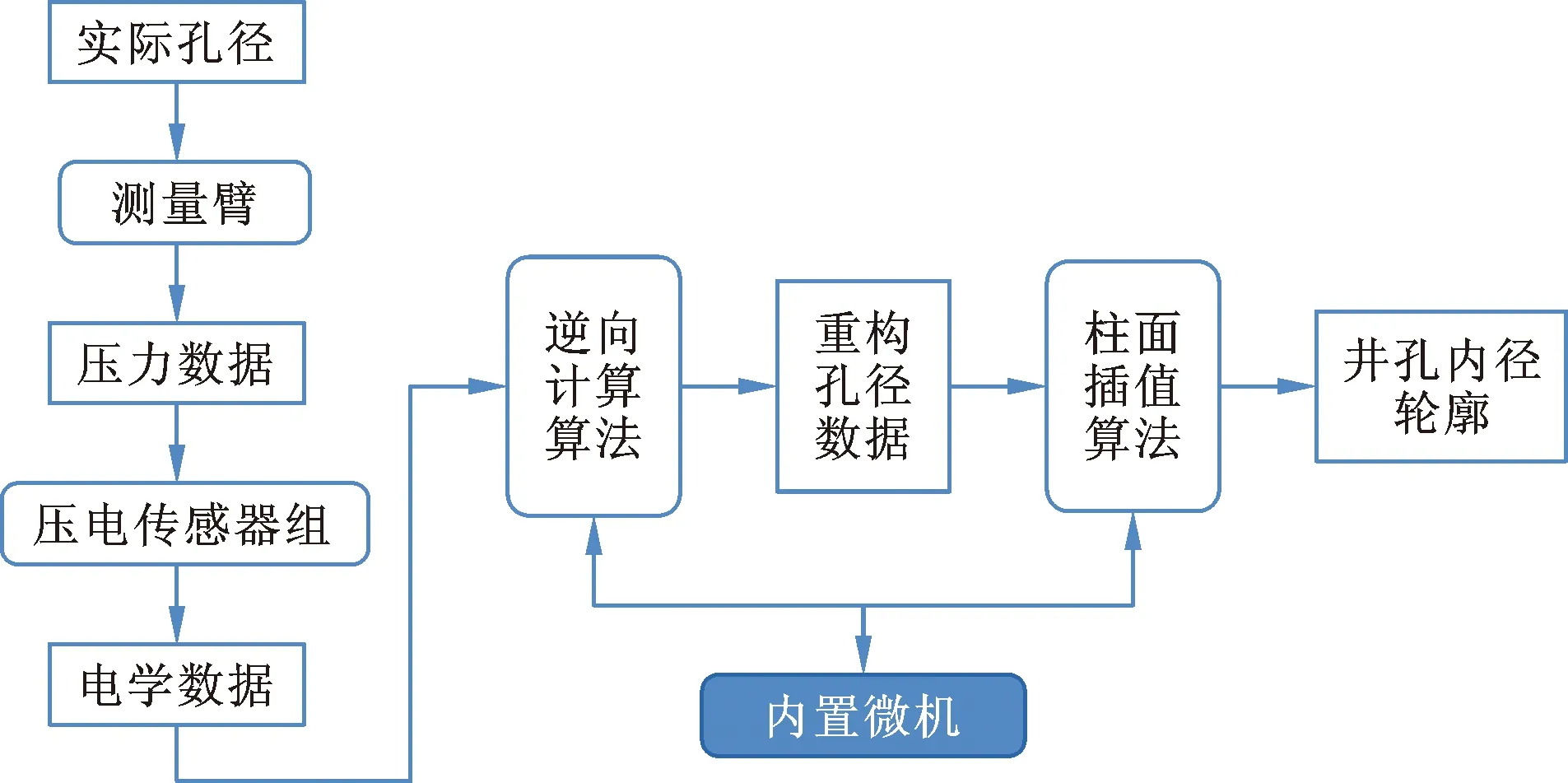
图1 井孔测量装置原理图Fig.1 Schematic diagram of borehole measuring device

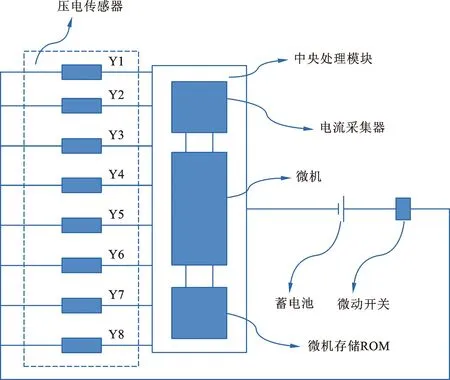
图2 内置微机原理图Fig.2 Schematic diagram of built-in microcomputer

测量设备上共安装8个带弹簧—压敏电阻的电路，用于记录并计算得到半径数据。测试过程中，通过上升记录装置记录位于不同高度时8个传感器的电流数据，因此每个高度上可获得8个电流数据。电流数据用Iij(xk)表示,其中下标i为传感电路编号，取值为1～8；j为测量行程编号，取值为1或2；xk为深度坐标，以井底为坐标原点，每0.5 m记录一次。得到压敏电阻受力Fij(xk)随xk变化的数据为：

(1)

式中:φi为第i个传感回路对应压敏电阻的力—阻函数；U为测试装置中总电源的电压值。

图3所示为测试装置示意图(共8根弹簧，图中仅展示一根),弹簧在自由不受力状态下的长度为ri0，测试半径Rij(xk)随xk变化的数据为：

(2)

式中:ki为第i个传感回路所对应的弹簧刚度。

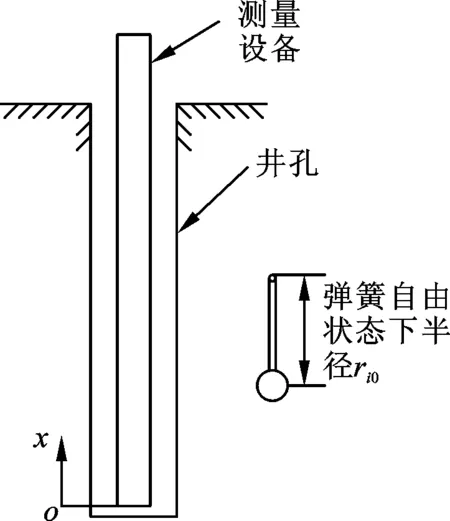
图3 测试示意图Fig.3 Test diagram

采用式(2)可得到N×8个数据，N为深度维度上的采样数，8为8个传感回路测试得到电流后通过计算所得到的半径数据的个数。在进行轮廓维度上的插值拟合计算时，由于8个测试数据分别对应于辐角：0、π/4、π/2、3π/4、π、5π/4、3π/2、7π/4,但没有2π处的数据，未形成封闭的圆柱壳体。因2π处数据与0处相同，因此在计算前需人工将N×8尺寸数据第一列复制到第9列，从而增加为N×9尺寸数据。

1.2 轮廓拟合插值算法

方法配套的程序所采用的插值方式为二维插值(圆周维度与井深维度)，其中可选的插值算法一共有5种：线性插值(默认)、最近邻插值、三次插值、Makima插值和样条插值。

(1) 线性插值[4]。设原始函数为柱函数，则每个点的半径长度的理论函数为ρ(φ,xk)，其中φ为圆柱表面上点对应的辐角，xk为深度坐标。首先对φ方向进行线性插值，假设已知柱面函数在p1=(φ1,xk1)、p2=(φ1,xk2)、p3=(φ2,xk1)、p4=(φ2,xk2)四个点处的函数值，则能得到xk方向上的插值函数：

(3)

随后在xk方向上进行插值，可以得到：

(4)

最后得到的线性插值结果为：

(5)

(2) 最近邻插值[5]。其算法原理如图4所示。从图4中可知，对于经过p1=(φ1,xk1)、p2=(φ1,xk2)、

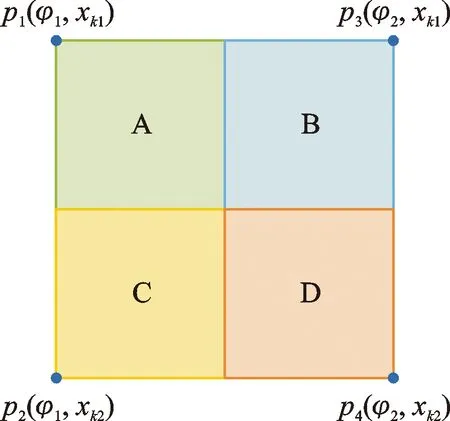
图4 最近邻插值示意图Fig.4 Nearest neighbor interpolation diagram

p3=(φ2,xk1)、p4=(φ2,xk2)四个点的二元函数，其最近邻插值结果为：A、B、C、D四个区域自变量对应的函数值分别等于p1、p2、p3、p4四个点对应的函数值。

(3) 三次插值[6]。相较于线性插值与最近邻插值，双三次插值因其高阶数与复杂度而被广泛应用于图像的平滑、锐化处理当中。程序中所使用的三次插值算法为基于BiCubic基函数的双三次插值法。其中BiCubic函数为：

(6)

当ξ取值为1时，BiCubic函数图像如图5所示。

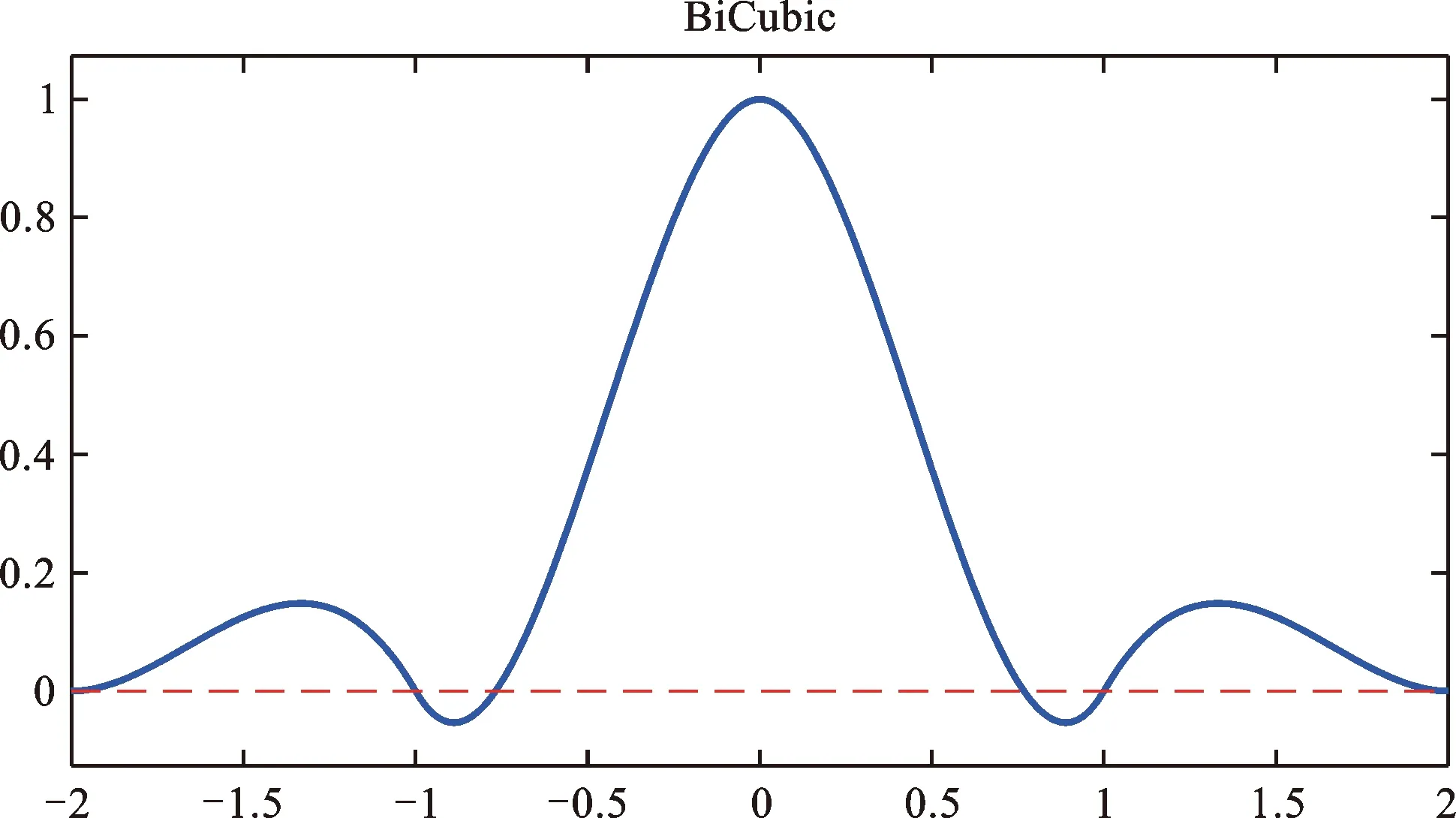
图5 BiCubic函数图像(ξ=1)Fig.5 Image of BiCubic function,ξ=1

对于待拟合的面函数ρ(φ,xk)，若已知其所经过的16个点坐标值ρ(φi,xkj)，其中i,j=1,2,3,4，结合BiCubic函数，可知其双三次插值拟合结果为：

(7)

(4) Makima插值[7]。为修正Akima插值方法，学术上又叫作修正Akima分段三次Hermite插值，通过连续6个点的采样值，基于双五次多项式和连续的一阶偏导数，对函数进行光滑的曲面拟合和内插。

(5) 样条插值[8]。又名三次样条插值。对于经过点(φi,xkj)(i=0,1,2,…,N；j=0,1,2,…,M)的二元函数ρ(φ,xk)，首先对其辐角进行插值计算。设φmin=φ1<…<φN=φmax，对于每个区间[xi,xi+1]都通过三次样条函数对其进行拟合，且整个定义域内的三次样条函数二阶连续。令第i个区间内的三次多项式为：

ρi(φ)=aiφ3+biφ2+ciφ+di

(8)

由于ρ(φ)在[φmin,φmax]上二阶连续，因此在每个节点处(除端点)满足以下连续性条件：

ρi-1(k)(φi)=ρi(k)(φi),k=0,1,2

(9)

由此可以得到3(N-1)个条件，结合N+1个插值条件，共有4N-2个条件，当给定两个端点的边界条件(视情况而定)时，便可确定插值函数的所有参数。

在得到辐角φ的插值函数后，以相同的方法进行深度维度的插值计算，最后计算得到整个井孔的插值轮廓函数。

五种插值方式的特点如表1所示。

表1 插值方式特点Table 1 Characteristics of interpolation method

通过插值计算得到的结果为柱坐标函数，随后将柱坐标向笛卡尔坐标系进行转换，得到用于绘制井孔轮廓的三维成像坐标值。根据所提出的大孔径井身结构三维成像方法的原理，可实现该方法对应装置的设计与配套软件的编译。

1.3 装置设计

本文所提出的大孔径井身结构三维成像测量装置如图6所示。图6中千斤顶的上端固定有支撑杆，支撑杆通过万向球轴承与井口测量平台连接；井口测量平台上固定有驱动电机，驱动电机上固定有驱动滑轮；驱动滑轮通过绳索与第一导向滑轮连接，第一导向滑轮通过第一绳索与测量仪器连接，测量仪器下端固定有配重块；测量仪配置有测量筒，测量筒四周通过螺纹连接副固定有测量臂，测量臂配置有弹簧套筒，测量筒还配置有微动开关和微机模块。其中测量仪的具体结构如图7所示。

图6 装置设计整体Fig.6 Overall device design1.轴承；2.固定销；3.第一导向滑轮；4.驱动电机；5.驱动滑轮；6.固定螺栓；7.万向球轴承；8.千斤顶；9.第一绳索；10.测量仪；11.配重块；12.固定销孔。

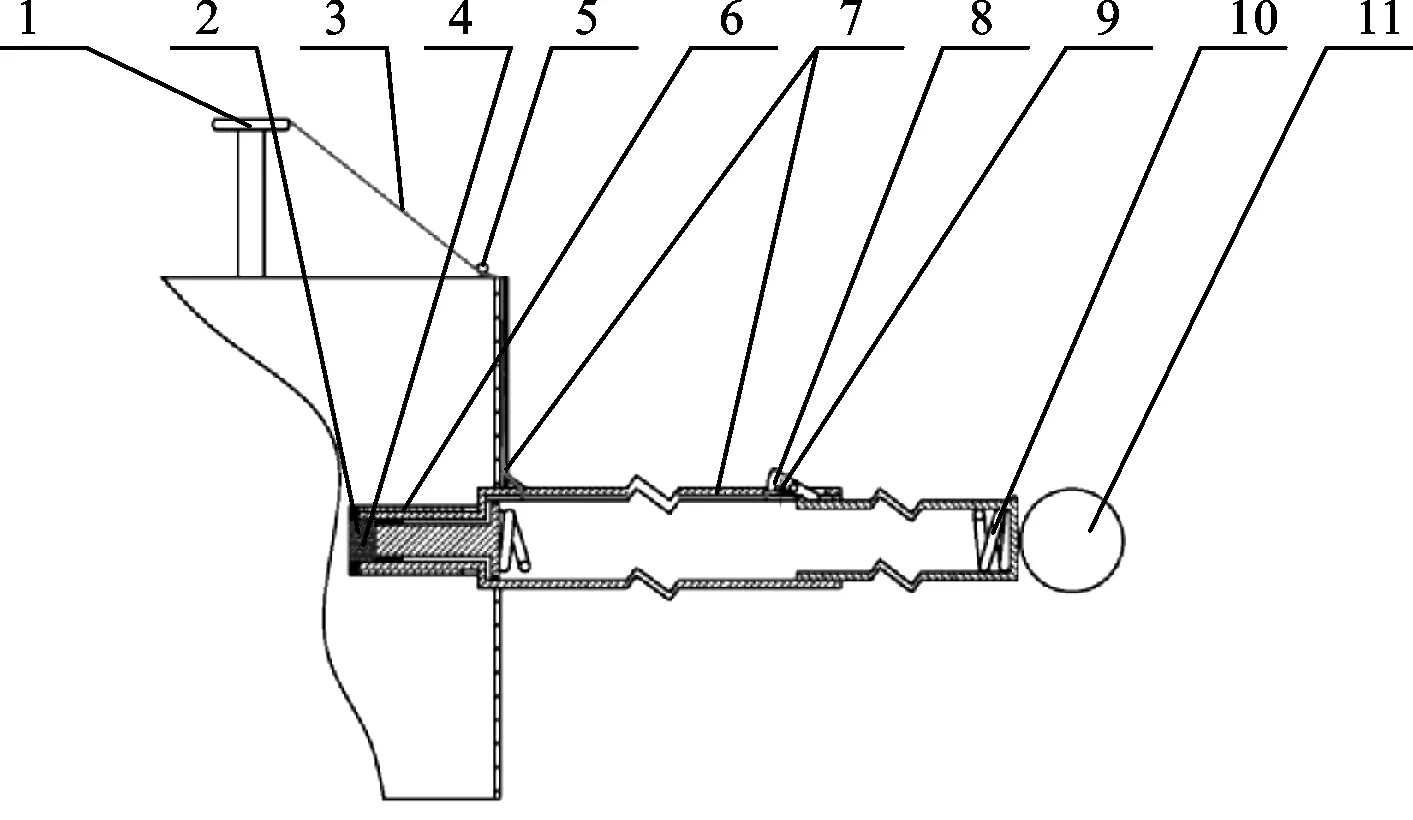
图7 测量仪结构图Fig.7 Structure diagram of measuring instrument1.固定线盘；2.橡胶；3.第二绳索；4.压电传感装置；5.第二导向轮；6.螺纹连接副；7.绳索导孔；8.弹簧卡扣；9.复位弹簧；10.伸缩弹簧；11.滚轮。

对于图7中的测量仪，其内部包含有8个方向测量臂的弹簧测试装置，具体结构如图8所示。基于上述装置设计及测试原理，在Matlab软件GUI编辑模块中实现数据测取处理后的轮廓计算与绘制程序的编译，从而实现井身结构图的自动刻画生成。

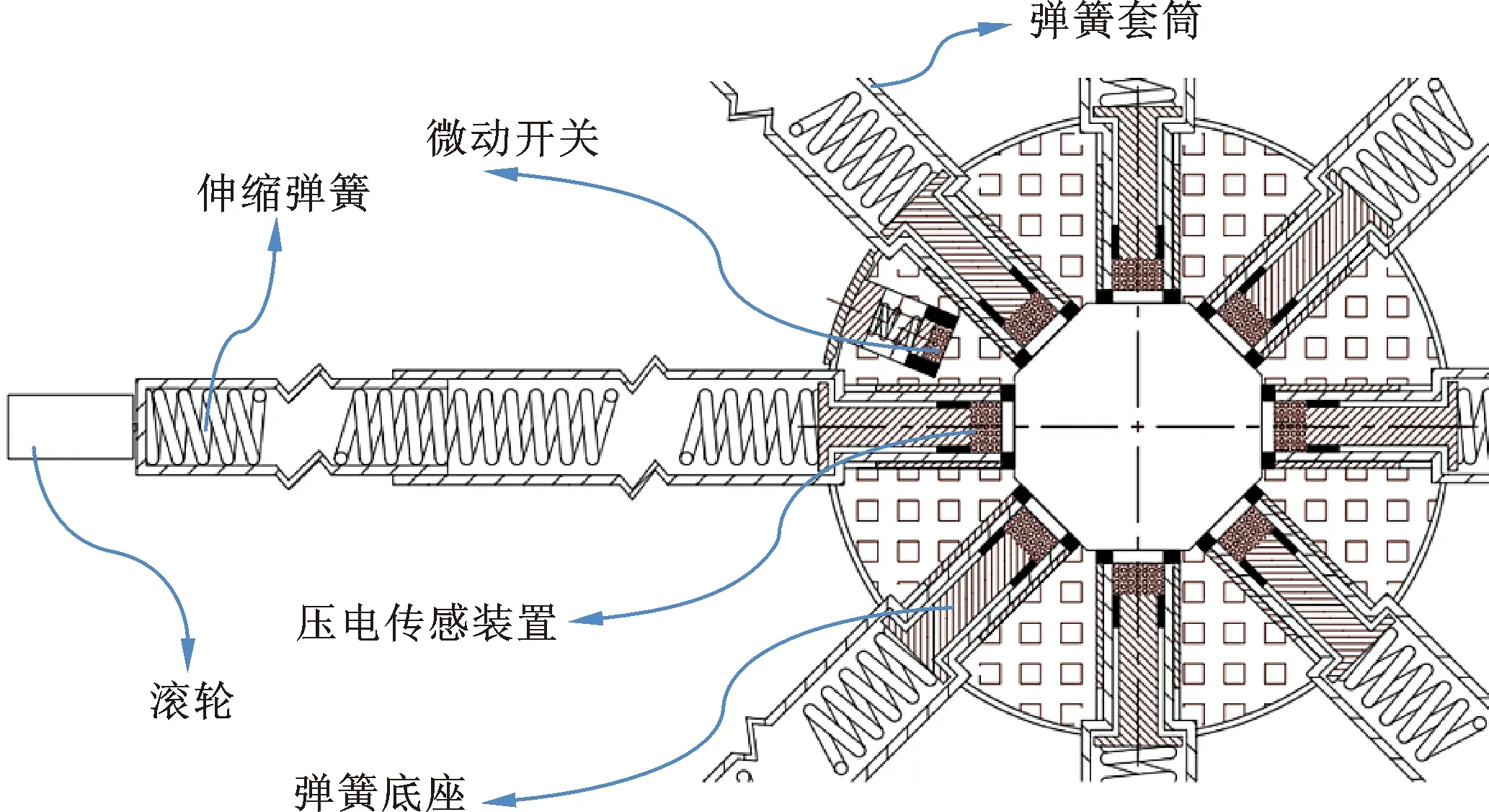
图8 带滚轮的弹簧伸缩臂Fig.8 Spring retractable arm with roller

2 仿真算例

为验证所设计的大孔径井身结构三维成像方法的可行性，本文选取平均直径800 mm、波动±100 mm、沿深度方向40 m随机生成的井孔轮廓为仿真研究对象，对轮廓沿圆周向每π/4弧度、沿深度方向每1 m深度的采样率进行数据采样，得到40×8的数据。为形成封闭圆环数据，将数据第1列进行复制，并增加到第9列，得到40×9的数据，最后将数据导入到自编软件中[9]。软件的界面如图9所示。

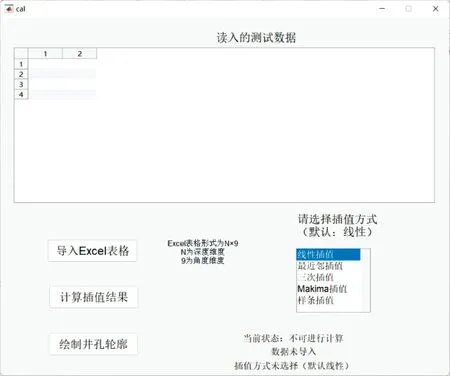
图9 井孔轮廓绘制软件界面图Fig.9 Interface diagram of well contour drawing software

将数据导入软件后选择插值计算模式，本文所提方法一共可选择五种插值算法，当未进行方法选择时，默认采用线性插值方法进行计算。随后进行插值数据的计算，最后将计算结果进行绘制，得到井孔的轮廓图。对于本案例所用数据，采用五种插值方式得到的轮廓如图10所示。由图10可知，除最邻近插值算法因算法简单快速导致结果精度较低外，其余四种插值算法所计算、绘制得到的结果形状相似，且轮廓过渡平滑，能较准确地还原重构井孔内壁的三维轮廓图。

在实际计算过程中，对于线性插值、最近邻插值、三次插值、Makima插值、样条插值这五种插值方法，计算插值解的时长分别为14.8 ms、13.1 ms、15.7 ms、35.2 ms与13.8 ms，相较而言Makima插值算法的计算效率最低而其余四种效率相当。因此对于数据量小的简单结构来说，其计算负载小，最近邻插值算法不仅还原准确度较差，效率也未得到显著提升，建议选用其余四种插值方法；对于数据量大的复杂结构来说，其计算负载大，Makima插值算法不仅计算效率较低，还原准确度也未得到明显提升，建议选用其余四种插值方法。

综上所述，应根据具体应用场合，选取不同的插值算法来进行井孔轮廓的插值计算，从而保证计算效率与还原准确度。

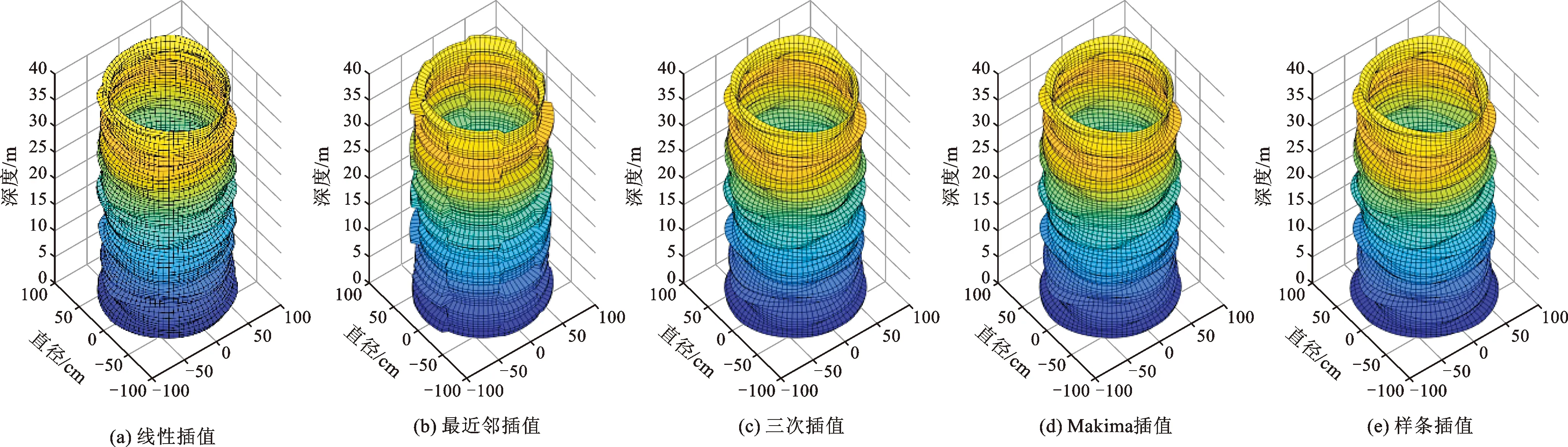
图10 不同插值方式下的井孔轮廓绘制图Fig.10 Well contour drawing with different interpolation methods

3 结论

(1) 本文方法能解决孔径测量难题，可根据钻孔孔径大小，设计相应的测量臂长度，依据孔径数据导入设计软件，自动绘制出井身结构三维模型，全方位展现井身结构，其直观性强、完整度高。

(2) 该方法可应用于大孔径地质钻探孔、地热井、地震地下流体观测井、大孔径工程桩孔及其它地下水资源开发井等工程项目的孔径测量和井身结构三维成像，可为同类工程项目提供参考。