基于承载力预压装配式框架结构的鲁棒性

倪 茜，刘娜娜,章伟豪

(西安科技大学建筑与土木工程学院，西安 710054)

近几年，随着中国建筑结构的发展和更新，预压装配式框架结构(prestressed concrete structure，PC)的应用越来越广泛，该结构是借助预应力将预先制作好的结构中楼板、墙体、梁柱等构件拉到现场进行拼装，使其连接更有效，大幅提高了结构节点强度，因而具有良好的完整性和抗震能力[1]。但由于PC结构节点连接形式多样化，使其节点处在循环荷载作用下易损坏，导致建筑结构极易发生连续性倒塌。因此如何增强PC结构的鲁棒性，避免结构的连续性倒塌成为中外建筑领域研讨的焦点[2-3]。

对于PC结构鲁棒性的问题，中外学者做了诸多研究。高扬[4]提出了以构件受力前后承载力变化为着眼点的重要性系数计算方法。耿方方等[5]研究表明在装配式框架结构抗震计算时考虑节点域刚度能大幅提高结构的屈服机制和性能水平。陈珊珊等[6]运用ABAQUS软件分析得出楼板与钢梁的结合使装配式结构连接节点承载力和刚度均显著提升。张航源等[7]研究表明：采用Pushover方法和冗余度指标可以有效地评价结构抗连续倒塌的鲁棒性。包超等[8]从易损性系数和重要性系数两个方面提出了结构鲁棒性定量算法。崔双双等[9]基于能量原理，提出考虑悬链线效应的结构鲁棒性计算方法。Mohammad等[10]提出一种结构连续倒塌的建模方法，来评估结构发生破坏时保留的完整程度，研究结构的鲁棒性，以便在特殊情况下避免结构的连续性倒塌。Sosso等[11]利用结构梁柱失效进行抗连续性倒塌计算，基于非线性动力学分析多层框架结构抗连续倒塌能力来评估结构的鲁棒性。

目前，现有的研究大都是结构的鲁棒性在水平作用下的，而结构的倒塌形态不仅仅是水平向的，所以对结构鲁棒性基于水平向的研究不能很好的应用于其他倒塌模式。在此基础上，现对结构的抗倒塌机理进行了有限元模拟，并利用SAP2000软件对结构进行了竖向非线性静力分析，通过比较PC结构和现浇结构结构(reinforce concrete structure，RC)的承载力和抗倒塌机理，研究PC结构的竖向连续倒塌抗力，以期为今后改善PC结构鲁棒性的案例提供参考。

1 抗连续倒塌鲁棒性理论计算

结构鲁棒性的研究针对的是结构中易损又重要的构件，这类构件的属性关系着结构是否会在单个构件失效后发生连续破坏。需通过对此类构件采取一定的措施来提高结构的鲁棒性，防止发生竖向连续倒塌。

1.1 构件易损性系数

构件易损性系数是衡量构件破坏程度的重要指标。在黄靓等[12]研究的基础上，针对单个构件对易损性系数做出进一步的研究，它反映了其抵抗荷载的利用率，作用在构件的内力随着利用率数值的增加而增加，构件易损程度也随之增高；当易损系数为0时，表明结构相对安全；易损系数接近1时，表明结构极其易损。易损性系数计算公式为

(1)

式(1)中：φi为构件i受轴向荷载影响的易损系数；Ni为作用在构件i的正截面应力，kN；Ni0为构件i的正截面承载力，kN。

现主要基于鲁棒性的结构竖向连续倒塌抗力问题。上竖向荷载先从顶板向梁传递，再由梁向柱传递。在板-梁-柱结构体系中，荷载传递到柱停止，因此构件易损性系数的评价指标选择框架柱的轴力。

1.2 构件重要性系数

结构构件的重要系数反映了被拆除构件的剩余结构承载力与完好结构承载力之间的差异。在高扬[13]的基础上提出重要性系数，对其推广至一般框架结构，引入Pushdown方法来计算结构承载力，该方法是将竖向荷载或位移施加在结构模型上，在分析过程中，施加在其上的荷载或位移逐渐增大。通过对结构刚度矩阵的不间断调整，使模型位移到达目标值。结构荷载增量的状态记录如图1所示。

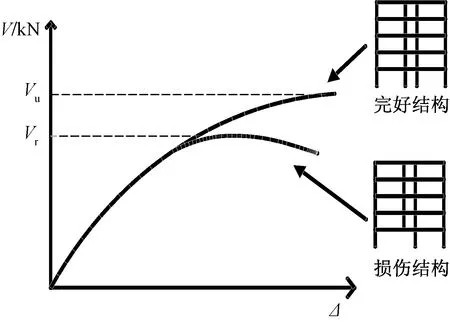
V为结构承载力；Vu为原结构竖向承载力；Vr为剩余结构极限承载力；Δ为位移变量图1 结构荷载图Fig.1 Structural loading diagram

构件重要性系数计算公式为

(2)

式(2)中：γi为重要性系数；Vu为原结构竖向承载力，kN；Vr为剩余结构极限承载力，kN。

1.3 结构鲁棒性系数

构件易损性与构件重要性系数广义上都体现了结构抵抗意外荷载的作用，目前中外学者考虑结构的鲁棒性时多将两者区分开来，忽略了构件既易损又重要的情况，只有将两者组合在一起才能全面评价结构的鲁棒性。因此，采用文献[8]提出的结构鲁棒性定量评价方法，即

(3)

式(3)中：R为结构鲁棒性系数。

2 分析模型的建立

2.1 工程概况

根据中国现行规范[14-16]，在SAP2000中建立同样的PC与RC框架对比模型，如图2所示。柱为常规矩形柱，柱脚固接于地面。结构尺寸参数如表1所示，结构设计参数如表2所示，梁柱平面布置如图3所示，PC结构梁柱配筋如图4所示，RC结构梁柱配筋如图5所示。

①、②为轴网图2 PC与RC框架模型简图Fig.2 Schematic diagram of PC and RC frame model

表1 结构尺寸参数Table 1 Structural dimension parameters

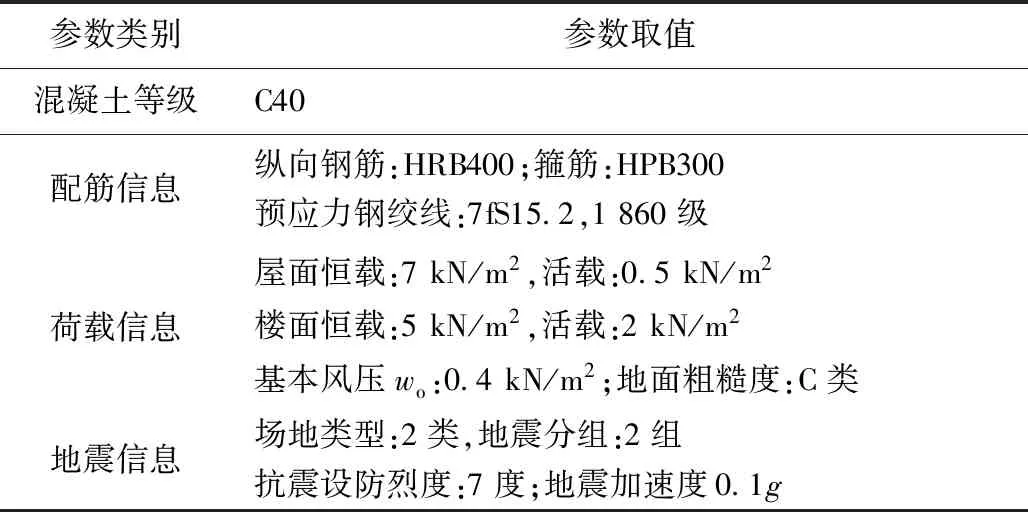
表2 结构设计参数Table 2 Structural designing parameters

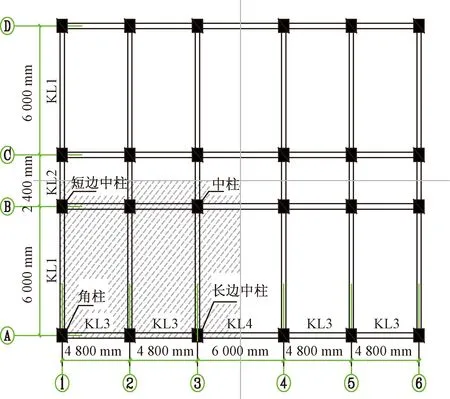
KL1～KL4为框架梁1～框架梁4；A～D为竖向轴网；①～⑥为横向轴网图3 梁柱平面布置图Fig.3 Layout plan diagram of beam and column

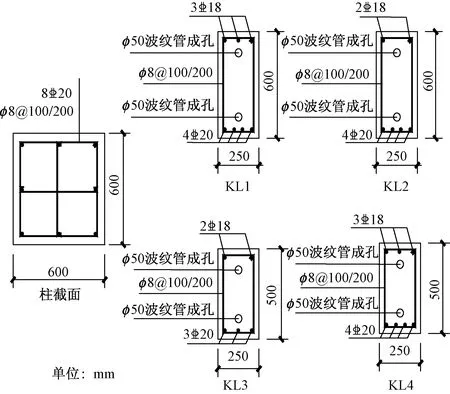
图4 PC结构梁柱配筋图Fig.4 Reinforcement diagram of PC structure beam and column

2.2 半刚性设置

一般情况下，RC结构的连接方式是梁柱刚接，PC结构的节点是由柱端和通过预应力钢筋形成的缺口梁组成[17]。对两种结构的节点选取半刚性连接。

周新潮[18]推导了预应力框架结构节点初始转动刚度计算公式为

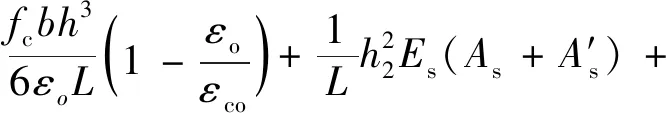
(4)

式(4)中：R为梁端的初始转动刚度；fc为梁的挠度；b为梁截面宽度；h为梁截面高度；εo为混凝土压应力达到fc时的压应变；εco为预压作用下梁的截面初应变；L为梁截面中心到位移计测量处的距离，一般取250 mm或300 mm；h1为预应力筋到截面中心的距离；h2为普通钢筋到截面中心的距离；Es、Ep分别为普通钢筋、预应筋的弹性模量；As、A′s分别为受拉区、受压区纵向普通钢筋的截面面积；Ap、A′p分别为受拉区、受压区纵向预应力筋的截面面积。

依据式(4)可以计算出梁柱节点转动刚度值如表3所示。

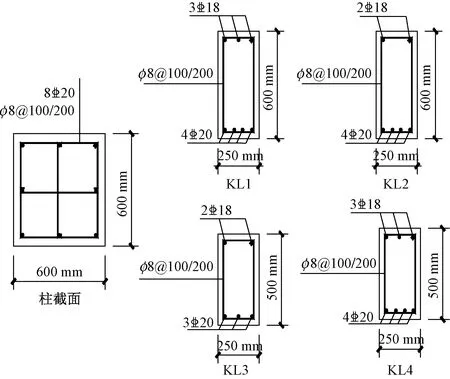
图5 RC结构梁柱配筋图Fig.5 Reinforcement diagram of RC structure beam and column

表3 节点初始转动刚度Table 3 Initial rotational stiffness of joints

2.3 预应力荷载处理

将预应力对PC结构的影响分为两部分。

(1)首先是PC结构中预应力筋形成的预应力。通过SAP2000中的参数设置，将其等同于一般外力作用于结构构件上。

(2)其次是预应力筋在PC构件截面中产生的影响。将其作为相同截面及位置的普通钢筋考虑，普通钢筋抗拉强度是通过预应力钢筋的设计值(fpy)与张拉时有效预应力(σpe)的差值来表示的。

该预应力钢筋初始张拉应力为1 395 MPa，预埋金属波纹管孔壁摩擦系数μ和每米局部偏差系数k根据规范取值，分别取0.25和0.001 5。

2.4 塑性铰的定义和设置

定义梁上的塑性铰选择自定义方法，定义柱上的塑性铰选择默认方式。具体做法为：利用SAP2000软件，释放梁两端端部主轴弯矩，输入表3中的数据，并在梁的0.1L和0.9L处(L为梁构件的有效长度)设置自定义弯矩铰M3。在柱两端0.05H和0.95H(H为柱构件的有效高度)处设置默认的PMM铰。塑性较的本构关系模型如图6所示，梁截面弯矩-曲率曲线如图7所示。

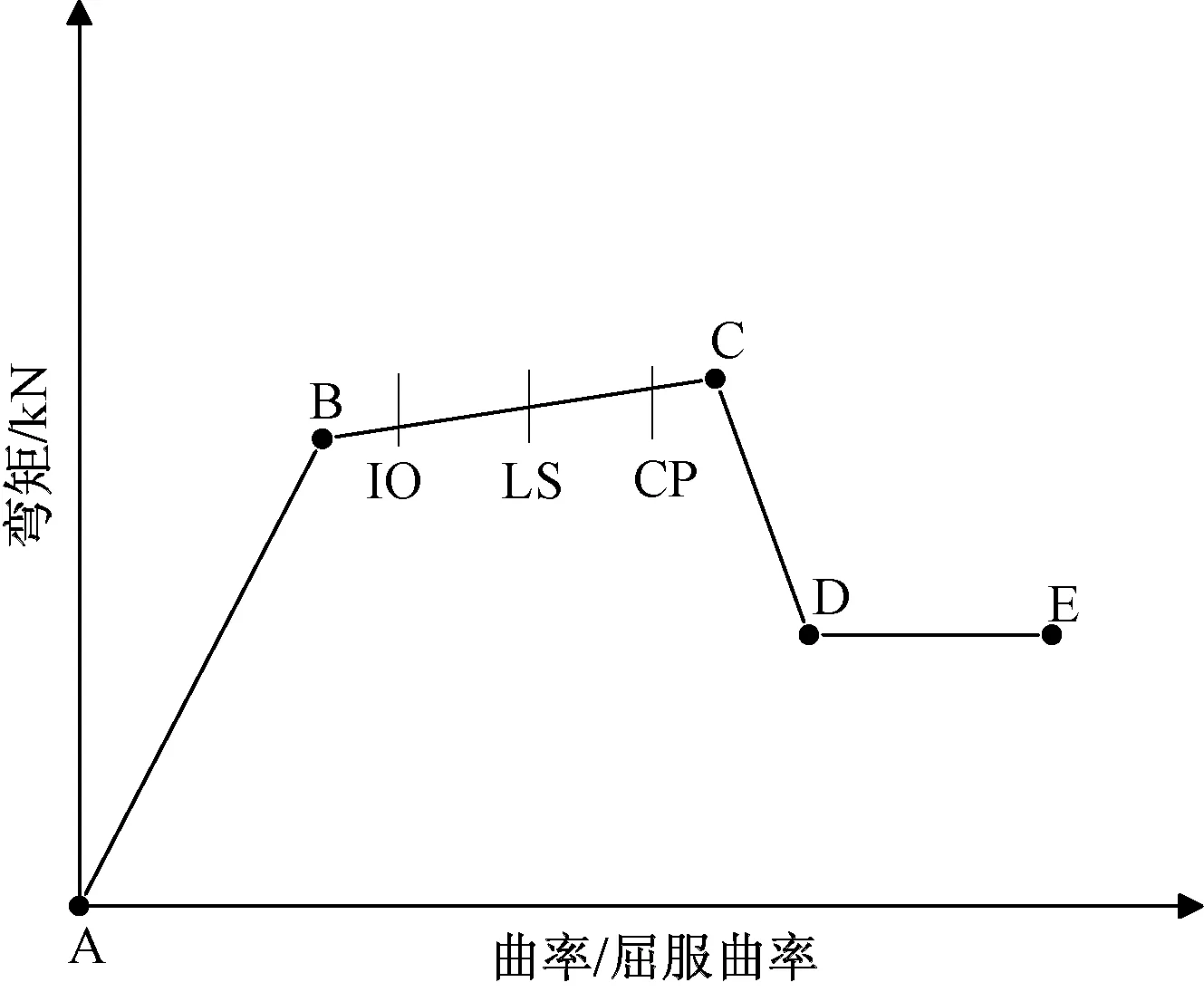
AB段为弹性段；BC段为强化段；CD段为卸载段；DE段为塑性段；IO(immediate occupancy)为安全节点；LS(life safety)为承载力节点；CP(collapse prevention)为尚未倒塌节点图6 塑性铰本构示意图Fig.6 Constitutive diagram of plastic hinge

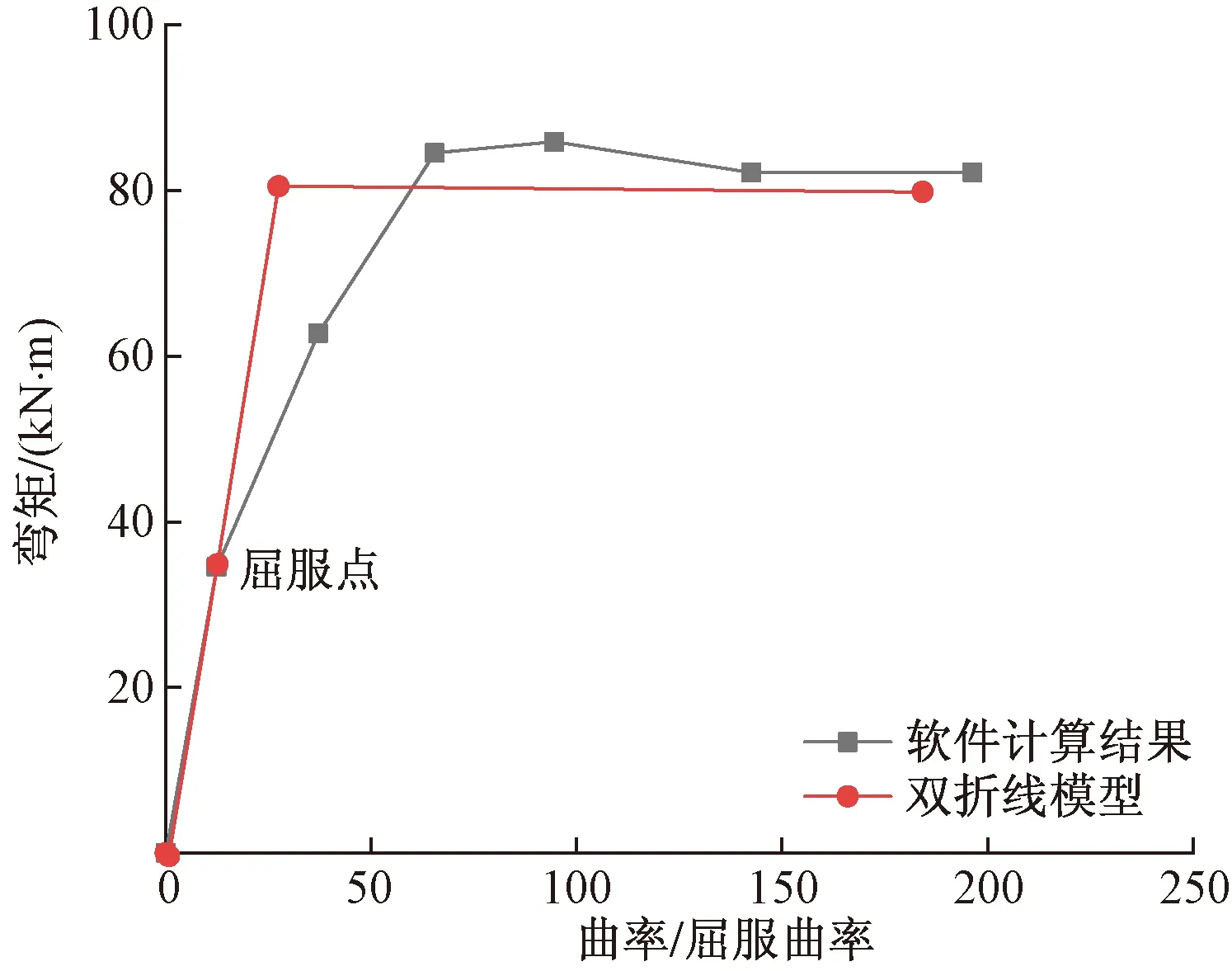
图7 梁截面弯矩-曲率曲线Fig.7 Bending moment and curvature curve of beam section

2.5 结构拆除工况设置

“Pushdown”分析法的具体做法为：逐渐施加竖向力，一直达到结构处于极限承载状态并且垮塌，得到此过程的位移-荷载关系曲线图。

将PC、RC框架结构模型的首层角柱、长边中柱、短边中柱、框架中柱依次拆除，设置为工况1、工况2、工况3和工况4，对比不同框架结构模型下的工况变化[19-20]。将控制点拟定为失效柱上方节点。

3 荷载系数与位移曲线

选择失效构件上方节点处作为变形参数，荷载系数与位移曲线的变化关系如图8所示，从荷载系数和位移曲线图(图8)可以看出PC结构与RC结构两者的承载力变化情况及抗倒塌机制。

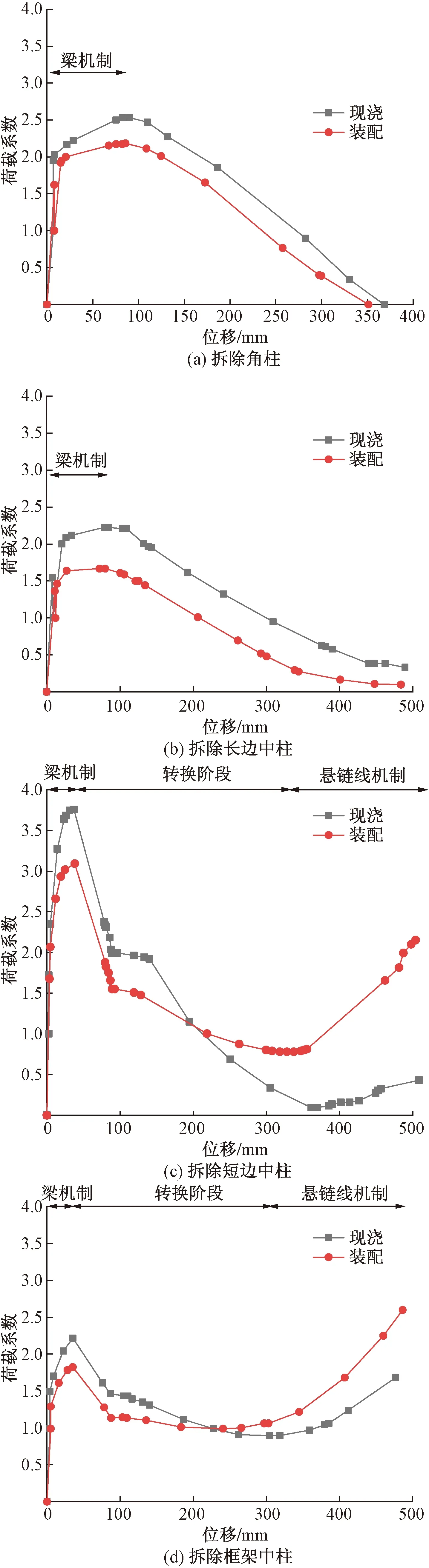
图8 荷载系数与位移对比图Fig.8 Comparison diagram of load factor and displacement

拆除首层角柱后，当竖向位移在0～35 mm内时，PC结构和RC结构荷载位移曲线均为线型。随着荷载增大直至屈服阶段，二者表现出了明显的差异，RC结构达到极限承载力的位移为90.37 mm，PC结构则为85.69 mm。在角柱失效后仅出现了梁机制，随着荷载增大，结构发生倒塌，发生倒塌时的RC结构竖向位移为272.49 mm，PC结构为299.28 mm。由此，拆除首层角柱时，PC结构的极限承载能力优于RC结构，延性更好。

拆除长边中柱后，当竖向位移在0～25 mm时，PC结构和RC结构荷载位移曲线均为线型。随着荷载增大直至屈服阶段，二者表现出了明显的差异，PC结构达到极限承载力的位移为78.03 mm，RC则为85.73 mm。长边中柱失效后仅出现了梁机制，此时数值模拟计算不收敛，结构已经倒塌，发生倒塌时的RC结构竖向位移为308.67 mm，PC结构为337.89 mm。由此可见，长边中柱失效后，PC结构的极限承载能力和延性也优于RC结构。

拆除短边中柱后，当竖向位移在0～20 mm内时，PC结构和RC结构荷载位移曲线均为线型。进入强化阶段后，RC结构达到极限承载力时位移为37.68 mm，PC则为38.29 mm，此时承载能力相对于角柱和长边中柱失效有明显区别，PC结构承受荷载的最大能力劣于RC结构，抗倒塌机制为梁机制；随着荷载持续增加，这时梁机制转换成悬链线机制，此时RC结构的竖向位移为360.87 mm，PC结构为327.71 mm。在此期间，PC结构在竖向位移约为200.00 mm时承载力超过RC结构。RC结构发生倒塌时的竖向位移为450.34 mm，PC结构为481.71 mm。因此，当短边中柱失效后，PC结构的极限承载能力略低于RC结构，但由于其倒塌时的竖向位移大于RC结构，足见其具有较高的延性。

拆除框架中柱后，当竖向位移在0～20 mm内时，PC结构和RC结构荷载位移曲线均为线型。进入强化阶段后，RC结构达到极限承载力时位移为36.54 mm，PC则为35.46 mm，两者位移较为接近。进入卸载阶段后，抗倒塌机制由梁机制转换为悬链线机制时，RC结构的竖向位移为301.98 mm，PC结构为227.01 mm，在此期间，PC结构在竖向位移约为240.00 mm时承载力超过RC结构。RC结构发生倒塌时的竖向位移为379.38 mm，PC结构为406.29 mm。由此表明，框架中柱失效后PC结构的极限承载力和延性都大于RC结构。结构倒塌时竖向位移汇总如表4所示。

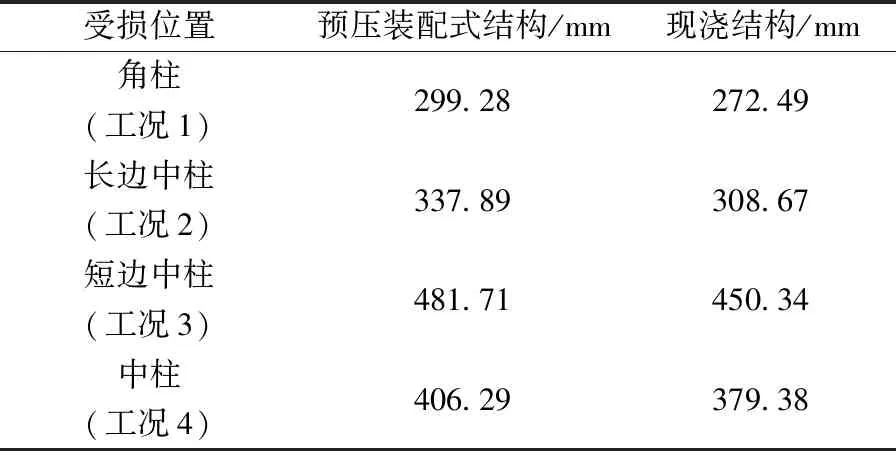
表4 结构倒塌时竖向位移Table 4 Vertical displacement during structural collapse

4 结构鲁棒性分析结果

4.1 构件易损性系数分析

PC模型和RC模型柱构件选取一致的相关参数(混凝土钢筋材料参数、柱的截面面积)。为方便计算，混凝土柱构件受力依据《混凝土结构设计规范》[14]按轴心受压构件计算处理，计算出的最大轴向压力为6 932.59 kN。根据式(1)计算构件易损性系数如表5所示。

由表5可知，易损性系数最大为工况4的PC结构；最小为工况1的PC结构，二者之差为0.074 7，差异较大，表明构件在结构中受损的可能性是不同的，且PC结构中柱最为易损。除工况2和工况4的PC结构外，其余工况RC结构的都大于PC结构。说明预应力钢筋的存在使角柱和短边中柱构件易损性系数得以减小，提高了结构的抗损伤能力。由此可见，在PC结构和RC结构中，构件易损程度为：框架中柱>长边中柱>短边中柱>角柱。

4.2 构件重要性系数分析

依据4.1节中的结论，位移观测点选取为中柱顶点。对完整结构进行Pushdown分析得到竖向承载力最大值，并将结果计入表6。根据式(2)计算结构构件重要性系数如表6所示。

由表6可知：构件重要性系数最大为工况2的RC结构，最小为工况3的RC结构。表6中数据显示出RC结构构件重要性系数均普遍大于PC结构，这说明在意外荷载作用下，RC结构构件在被破坏后，对其整体结构性能的影响程度相较于PC结构更大。由此可见，在PC结构和RC结构中，构件重要程度为：长边中柱>框架中柱>角柱>短边中柱。

纵观各个构件不难发现，长边中柱和中柱重要性系数均优于角柱和短边中柱，这说明距离结构中心位置越近，结构构件承受的荷载就越大，要求也就随之提升，因而构件重要性系数也越大。

4.3 结构鲁棒性系数分析

为了得到结构鲁棒性系数，有必要对原结构1/4框架部分的底部框架柱竖向荷载进行分析，通过式(4)计算分析可知：在考虑结构节点半刚性特性的前提下，PC结构的鲁棒性(3.197)略小于RC结构(3.257)。因此，节点的半刚性不利于结构抗竖向连续倒塌的鲁棒性。

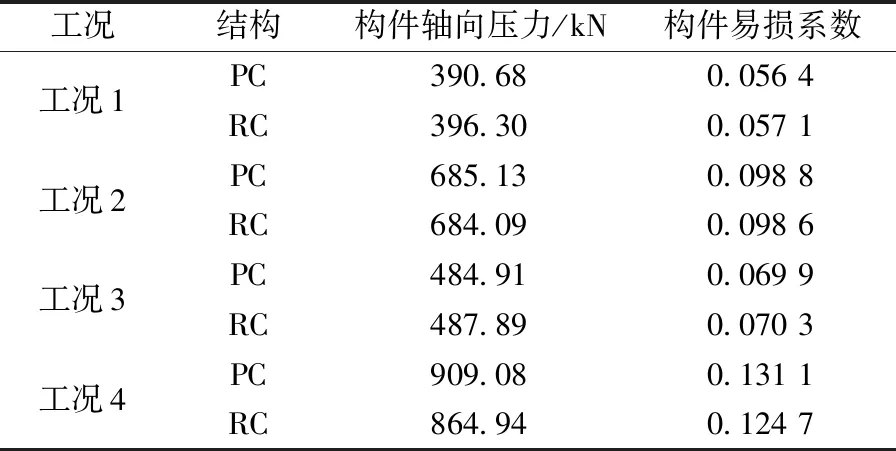
表5 构件易损性系数Table 5 Component vulnerability coefficient

表6 构件重要性系数Table 6 Component importance coefficient

5 结论

通过对PC结构和RC结构模型进行非线性静力分析，对比了两种结构的承载力变化情况和抗倒塌机制的变化规律，研究了两种结构的抗倒塌模式、延性及鲁棒性，得到以下结论。

(1)拆除两种结构角柱、长边中柱的倒塌机制均为梁机制，而拆除短边中柱、中柱的倒塌机制均为悬链线机制，两种结构的倒塌模式相似。因此，预应力钢筋的存在对PC结构和RC结构的倒塌模式影响不大。

(2)对比两种结构荷载系数与位移曲线得到拆除各柱最终倒塌时的竖向位移PC结构大于RC结构。其中，工况1：PC较RC提高了9.83%；工况2：PC较RC提高了9.47%；工况3：PC较RC提高了6.97%；工况4：PC较RC提高了7.10%。因此PC结构的延性优于RC结构，有利于结构抵抗竖向连续倒塌。

(3)结构鲁棒性综合考虑了结构的重要性和易损性，在节点半刚性设置下PC结构鲁棒性略小于RC结构，可见节点的半刚性使结构的鲁棒性降低。因此，若要提高PC结构的鲁棒性，必须提高PC结构节点连接刚度。