基于电动车研发成本补贴的回报共享制度研究

冉翠玲

(上海理工大学 管理学院， 上海 200093)

近年来在国家一系列政策的扶持下，无污染、轻噪声的电动车产业迅速发展。由于新兴产业的电动车行业具有高成本、高复杂性、高风险、高外溢性的特点，同时还具有市场的不确定性，这些特点都会导致电动车企业研发投入的积极性偏低，造成电动车市场失灵[1]。当前国家解决电动车企业研发市场失灵问题的措施就是补贴政策[2]。国家直接财政补贴是鼓励电动车企业研发的有效工具[3]。因为政府实施的一系列有关基础设施、道路权利、财政补贴、充电桩建设等政策，促进了电动车产业蓬勃发展[4]。Lee[5]研究发现政府补贴政策与企业规模大小无关。Shao等[6]研究发现价格折扣政策对电动车产业的优劣程度有关。Gu等[7]研究表明新能源汽车产业发展补贴政策分两个阶段，发展初期补贴消费者，后期补贴企业有利于整个行业利益最大化。政府财政补贴政策是否有效激励电动车企业加快技术水平的研发，关键在于国家财政补贴制度设计能否在电动车企业实践层面得以实现。

孙绍荣[8]提出制度设计的符号系统，使制度具有工程化设计方法和分析方法，为制度研究从定性的理论分析转向可具体操作的技术发展奠定基础。孙绍荣等[9]从制度设计的角度论证了控制企业努力水平与税率的关系，证明税收起到调节水污染型企业的生产速度，并且有利于水资源的保护。据此，本文利用制度设计中的回报共享制度对电动车企业研发的努力水平行为进行研究，从行为分析及制度研究的角度为政府补贴电动车企业研发有效性提供决策支持和科学依据。

1 电动车企业研发行为分析和回报共享制度孙氏图

电动车企业研发行为的生产具有正的外部性，比如减少温室气体的产生、增加续航里程、减少环境的噪声污染等。电动车企业建立的公用充电桩，造成事实上享用的除了生产者(或投资者)之外，还有许多其他的潜在个体。并且电动车企业投入的研发行为及其成本很难在短时间内观测，电动车研发企业的特点符合回报共享制度的使用条件。回报共享制度是一种多个体联合起来完成任务的任务分担制度，特点是群体收益由成员平均共享，但个体的行为成本却是各自独立承受的，因此“回报共享，成本独立”是回报共享制度的基本特征。

为了方便研究，假设回报共享制度系统里面的群体在分配上的独立性。群体中全部个体电动车企业获得的行为回报之和等于群体的全部产出，并且只来自于群体的产出，群体不保留任何剩余但也不亏损。假设回报共享制度系统里面的个体电动车企业具有同质性，即群体中所有的个体电动车企业都是相同的，无任何差异。群体中的个体电动车企业的同质性，免去了对每一个个体电动车企业分析的麻烦，对任何制度进行分析的时候，只要分析一个个体电动车企业就可以了解全部个体电动车企业的情况。

孙氏图[8]是制度设计的工程化方法，把电动车企业的研发行为系统用制度设计的图形符号表述出来。孙氏图中的产出是电动车企业的努力水平的促进器，研发电动车的成本是电动车企业努力水平的抑制器，努力水平越高，企业回报越多。假设电动车企业共享回报是努力水平的增函数。

图1为两个电动车企业的回报共享制度孙氏图。图1表示企业1的研发努力水平e1的提高，则共享回报r会增大，同时企业2的研发努力水平e2的提高，则共享回报r也会增大，回报r是企业1与企业2共同享受的。

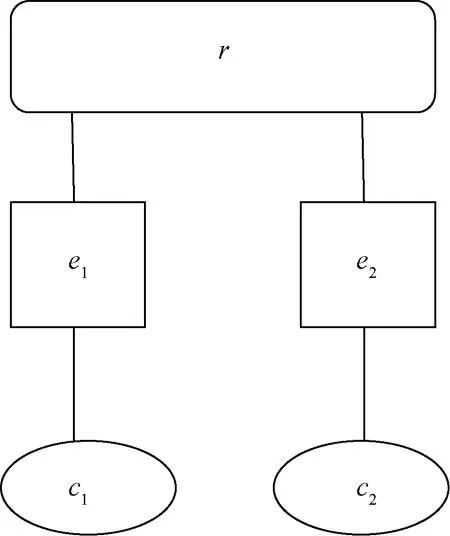
图1 回报共享制度的孙氏图[注]孙绍荣，《制度工程学》，第117页。

2 回报共享制度下的电动车企业研发的努力水平均衡点

假设某地电动车研发企业的个数为n，并且电动车企业为完全理性人，电动车企业i的研发努力水平是ei,i={1,2,…,n}，则电动车企业个体j的产出rj与其研发努力水平ej的函数[注]本文所有公式来源于孙绍荣的《制度工程学》第117—131页。为

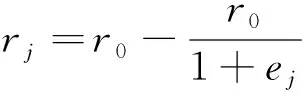
(1)

式中r0≥0,ej≥0，r0为电动车研发企业个体产出的极限最大值。

当有n个电动车研发企业， 则电动车研发企业群体的产出为

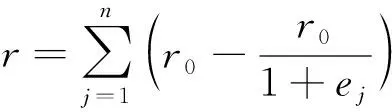
(2)

在回报共享制度下，个体电动车研发企业的回报ri与产出rj不一定相等而是与群体企业的研发努力水平有关，即

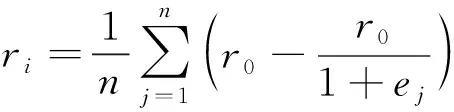
(3)

设ci为个体电动车企业i的研发行为成本，在回报共享制度下有ci=ei(i=1,2，…,n)。回报共享制度下的个体电动车企业i的研发行为效用函数为

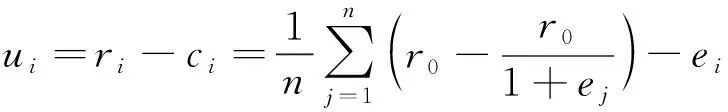
(4)

对研发行为效用函数求导，并令其等于零，即

(5)

由此得到个体电动车企业i的最优的研发努力水平为

(6)

在回报共享制度下，个体电动车企业的研发努力水平越高群体获益更大。如果电动车企业i是完全理性人，则他的研发努力水平将会在式(6)所决定的水平上。同时得到个体电动车企业i的产量：

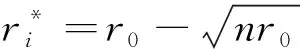
(7)

2.1 回报共享制度的变形1——串联合作制度

2.1.1 串联合作制度的定义和假设

合作制度是指多个个体联合起来形成更大的实力来承担任务的制度，同时本章中的合作是指多个电动车研发企业个体在研发行为上相互协调，所得的收益超过各个研发企业个体的收益之和的情况，即合作形成的群体效益是个体的收益“超可加”。

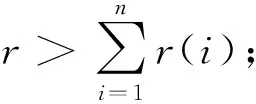
串联合作制度是指各合作参与方对群体的收益具有乘法效应的情况，即必须全部参与者都努力，群体才有收益，只要有一个参与者的努力水平为零，群体的收益就为零。群体的收益多少取决于群体中努力水平最低的个体。合作的乘法效应的定义为

r=f[min(e1,e2,…en)]

(8)

图2为两个电动车研发企业进行串联合作的孙氏图，图中所示电动车研发企业1在前参与研发合作行为，电动车研发企业2在后接着参与到群体的研发行为，电动车研发企业1合作研发的努力水平e1的效用是con1，接着con1与e2一起产生合作的效用con2，con2产生r群体收益，这是群体中只有两个个体的特例，群体中个体增加以此类推。con1可以看作是电动汽车的电池研发行为，此时电动车还没有制造出来，没有生产价值。con2可以看作是电动车最后的装配成整车可以出售，有了使用价值即产生了回报r。这是两个电动车企业共同努力，通过效用con1与con2产生两个个体电动车企业的共享回报。

图2 串联合作制度的孙氏图 (双个体且e1在前)[注]孙绍荣，《制度工程学》，第125页。

2.1.2 串联合作制度的数学模型

假设合作研发电动车群体中有n个电动车研发企业，每个研发企业平分群体的集体收益，则电动车研发企业i的回报函数定义为

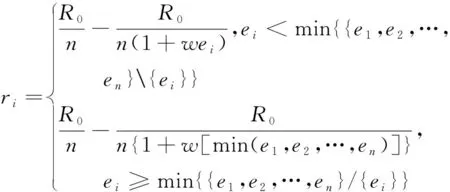
(9)

式中：R0>0意义是形成合作的群体能够取得的最大群体收益上界，由群体特点和合作行为特点所决定；ei≥0，ω>1，ω的意义是合作群体对个体行为效用的放大作用；{e1,e2,…en}{ei}表示在集合{e1,e2,…en}中剔除元素{ei}；min{{e1,e2,…en}{ei}}表示在集合{e1,e2,…en}{ei}中求最小值的元素。

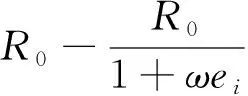
当电动车研发企业群体有n个研发电动车企业参与串联合作研发时，电动车研发企业i的效用函数为

ui=ri-ci=

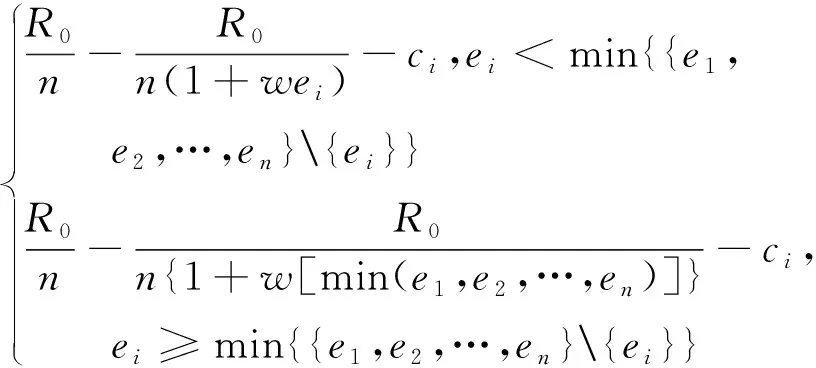
(10)

对式(10)关于努力水平ei求导得

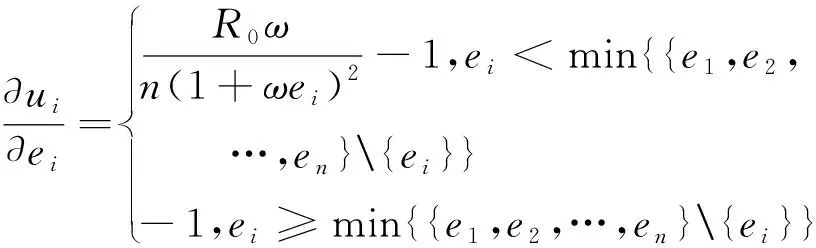
(11)

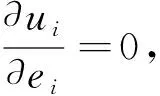
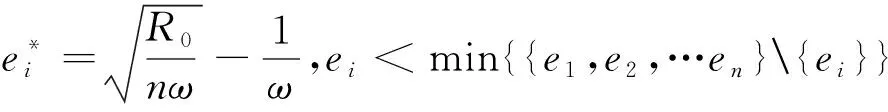
(12)

根据上面的分析得到以下结论：

2)在合作研发群体中，各个研发个体的努力程度是互相影响的，个体企业研发行为越努力，参与合作的个体企业越会提高自己的研发努力水平。

2.2 回报共享制度的变形2——并联合作制度

2.2.1 并联合作制度的定义和假设

并联合作制度是指各参与者的收益只具有超可加性效应的情况，即群体的效益大于各个参与者单干的效益之和，但没有乘法效应，因此与串联合作制度不同，如果有参与者努力水平为零，群体仍然可能有效益。

图3为两个电动车个体研发企业并联合作制度的孙氏图。图中e1、e2一起指向con表示研发企业1 和研发企业2的合作行为会导致con的结果产生。但是不会直接对e1、e2有影响，con的出现使得r增加，同时研发企业1 和研发企业2为了获得r的收益愿意提高努力水平。

图3 并联合作制度的孙氏图 (双个体且并联合作)[注]孙绍荣，《制度工程学》，第130页。

2.2.2 并联合作制度的数学模型

(13)

式中：R0>0,n≥1,ei≥0,ω>0,e0>0；R0表示并联合作行为所决定的个体提高努力水平所能获得的最大群体收益的上界；e0表示群体产生收益所需要的最小的合力，即使群体产生收益所需要的所有参与者的努力水平之和(并且所有参与者的努力水平之和是超可加的和)的最小值，它与合作行为的性质有关。ω表示并联合作制度下的个体努力水平在合作时的放大系数，ω=1表示合作群体对个体行为既没有放大作用也没有缩小作用，此时的群体效益只是各个个体效益的简单和。ω<1表示表示合作群体对个体效益有缩小作用，此时个体在合作群体中发挥的效益不如独立完成效益大，即群体中的内耗严重情况，本章中规定ω>1表示合作群体对个体行为具有放大作用。

当电动车研发企业群体有n个研发个体企业参与并联合作研发时，个体研发企业i的效用函数为

ui=ri-ci=

(14)

对式(14)关于努力水平ei求导得

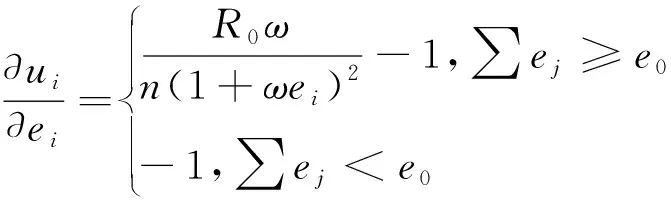
(15)

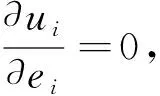
(16)

根据上述分析得到结论：平均分配下的并联合作制度下的个体努力水平的最优值等于平均分配收益的串联合作制度下的个体不利水平的最优值，所以影响并联或者串联合作制度的因素相同，电动车研发群体的参与个体越多，努力水平的最优值就越低，并联合作制度收益上限R0越高，个体努力水平的最优值就越高。在管理实践中还是能够采取一些措施来提高个体电动车企业的研发努力水平的。

上述3种形式的回报共享制度本质上都是单纯的回报共享制度，只是形式上的不同，都存在群体中个体越多则个体的研发努力水平越低的问题。因此在可能的情况下，制度设计者应当尽可能地分割产出，从而使群体尽可能地变小一些。为了使制度更好地运用在实际管理中，必须对各种回报共享制度进行改进，接下来以单纯的回报共享制度为例加以改进。

2.3 改进的具有成本补贴的回报共享制度

具有成本补贴的回报共享制度是为了提高个体企业努力水平的改进型制度，其特点是回报共享、成本独立，根据个体企业的研发成本付出给予“成本补贴”，因为个体企业的研发投入成本是独立的，研发成本投入直接与个体企业努力水平正相关。所以“成本补贴”就是个体企业提高努力水平的一个回报促进器，具有成本补贴的回报共享制度下的努力行为水平一定会比单纯的回报共享制度下的行为努力水平要高。

图4为具有成本补贴的回报共享制度的孙氏图，其中rsi为针对个体电动车企业i的研发成本补贴，是研发企业的促进器，增加成本补贴对研发努力水平起促进作用，加快电动车企业发展的步伐。

假设对电动车企业i的研发行为成本补贴rsi是ci的线性函数，即

rsi=kci=kei

(17)

图4 具有成本补贴的回报共享制度的孙氏图[注]孙绍荣，《制度工程学》，第121页。

所以在具有成本补贴的回报共享制度中，电动车企业i的回报ri与群体的研发行为努力水平的函数为

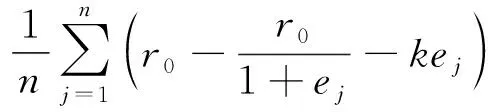
(18)

同时电动车企业i的效用函数为

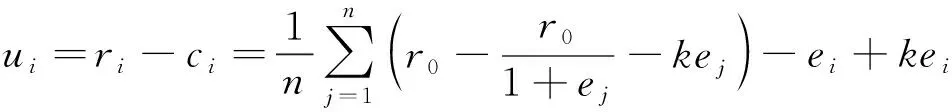
(19)

效用函数式(19)对电动车企业i的研发努力水平ei求导，并等于零，有

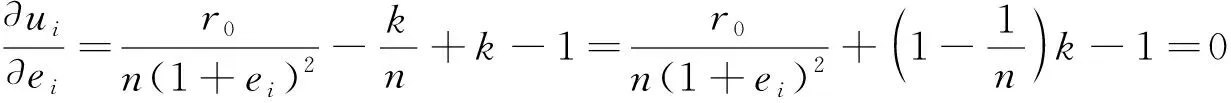
(20)

所以具有成本补贴的回报共享制度下，电动车企业i的最优研发努力水平为

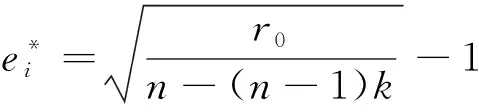
(21)

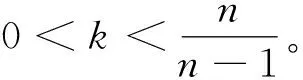
由于n>n-(n-1)k，比较式(6)与式(21)得到

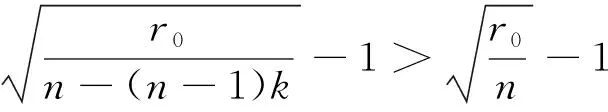
(22)

即具有成本补贴的回报共享制度下的个体企业研发努力水平要高于单纯的回报共享制度下的个体研发努力水平。

事实上，只要群体的产出效率充分高，也就是说产出与消耗的成本之比比较大，制度设计者通过调节k，使n-(n-1)k=1，即k=1，就是表示对个体成本实行完全补贴，此时有

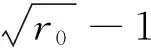
(23)

即具有成本补贴的回报共享制度下的个体企业研发努力水平最优值与群体收益最大的努力水平最优值相等。

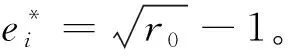
3 数值模拟

根据上述分析，在r0=100,n=9时得到图5的数值模拟结果。

图5 数值模拟结果

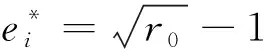
4 结论

运用制度工程学的回报共享理论，运用3种形式的回报共享制度对国家给予电动车企业的政策扶持行为进行研究。首先建立单纯的回报共享制度，并得到个体电动车企业效用最大化情况下的最优努力水平。其次建立两种变形的回报共享制度，分别得到群体最优努力水平及个体最优研发努力水平。研究发现群体中电动车企业个数越多，个体企业的研发努力水平就越低。可以理解为个体不努力工作，反而对别人的努力起到阻碍作用，所以必须对回报共享制度加以改进。最后建立改进的具有成本补贴回报共享模型，发现此时的个体企业研发努力水平要高于单纯的回报共享制度下的个体研发努力水平。根据上述研究分析，当通过调节成本补贴函数的系数k，使k=1时，也就是对研发企业实行完全补贴政策下，实现了具有成本补贴的回报共享制度下的个体企业研发努力水平最优值与群体收益最大的努力水平最优值相等。