基于SRCKF的带有乘性相关噪声的滤波方法研究*
沈念如
(南京理工大学 南京 210094)
1 引言
现阶段,卡尔曼滤波器(Kalman Filter,KF)[1~2]是在目标实时跟踪系统中应用最为广泛的一种方法,传统卡尔曼滤波只适用于线性系统,而对于非线性目标跟踪领域[3],扩展卡尔曼滤波(Extended Kalman Filter,EKF)[4]是对非线性函数进行一阶泰勒级数展开并忽略高阶项,在非线性特性较强的时候,不可避免会引入较大地线性化误差以至于会造成滤波发散。无迹卡尔曼滤波(Unscented Kalman Filter,UKF)[5~6]利 用 无 迹 变 换(Unscented Transform,UT)在估计点附近确定采样点,对非线性分布的统计量具有较高的计算精度,然而UT变换需要对矩阵进行乔利斯基分解容易导致算法停滞。平方根容积卡尔曼滤波(Square Root Cubature Kalman Filter,SRCKF)[7~9]采用协方差矩阵的三角分解因子代替协方差矩阵进行递推更新,成功避免了非正定矩阵乔利斯基分解的问题。然而随着非线性系统规模和复杂性的扩大,由于各种难以测量的干扰,不确定的传输时延和损失广泛的存在,其中之一便是随机乘性噪声,广泛存在于系统的工程应用当中。针对具有此类乘性相关噪声[10,13]的非线性系统结合SRCKF滤波框架,可以有效地提高滤波地精度。
2 非线性滤波方法
2.1 扩展卡尔曼滤波
EKF算法是建立在线性卡尔曼滤波基础上,其主要思想是对非线性系统模型围绕滤波值做Taylor级数展开并略去二阶及以上的高阶项,得到一个近似的线性化的系统模型,然后对该模型做线性化求解。系统的离散非线性状态及观测模型如下:

其中wk∈Rn,vk∈Rm分别表示为过程噪声和观测噪声,且它们为互不相关的均值为零,协方差分别为Qk和Rk的高斯白噪声序列,Xk∈Rn,Yk∈Rm分别为k时刻状态向量和观测向量,f(·)和h(·)分别为非线性状态运动方程和非线性观测方程。应用线性Kalman滤波原理其递推步骤如下所示:
1)先验状态一步预测:

2)先验状态一步预测误差协方差:

3)观测一步预测:

4)卡尔曼滤波增益:

5)后验状态更新:

6)后验状态误差协方差:

不难看出,EKF递推算法公式与线性Kalman滤波公式近乎一致,只不过EKF的非线性运动方程和观测方程因为一阶线性化,导致系统模型使用Jacobian矩阵代替状态转移矩阵和观测矩阵;此外EKF算法是对非线性函数进行一阶Taylor级数展开并忽略高阶项,在非线性特性较强的时候,不可避免会引入较大地线性化误差以至于会造成滤波发散。
2.2 改进SRCKF滤波
基于乘性相关噪声的平方根滤波方法,首先要建立带有乘性相关噪声的离散非线性系统模型[11~12],如式(8)所示。
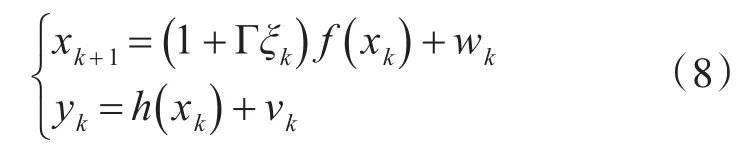
其中f(·)和h(·)分别为非线性状态方程和观测方程,xk∈Rn,yk∈Rm分别为系统的k时刻状态向量和观测向量,wk∈Rn,vk∈Rm为互不相关的过程噪声和观测噪声离散序列,分别服从零均值方差为Qk和Rk的高斯分布,ξk∈R1为k时刻乘性噪声,服从零均值方差为Uk的高斯分布,且ξk和vk互相关,互相关协方差矩阵为Gk,Γ为已知常数。
若X和Y满足联合高斯分布,根据相关理论知识,则其条件概率也满足高斯分布,其均值和协方差如式(9)所示,由于状态模型和观测模型中乘性噪声与观测噪声互相关,由此考虑乘性噪声和观测序列在联合高斯分布情况下,其条件概率的分布也满足高斯分布,其均值M和方差J如式(10)所示。
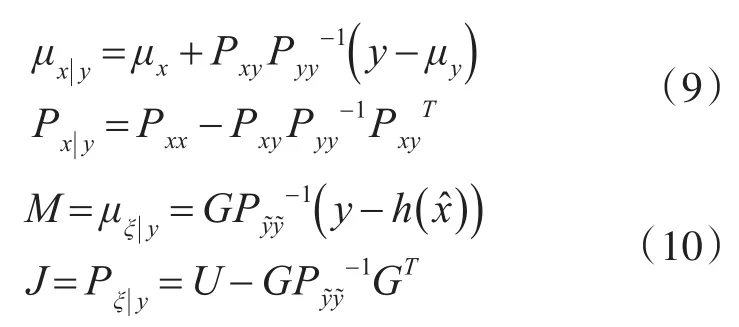
由式(10)可知M∈R1,J∈R1,因此在已知k时刻后验观测条件下的状态滤波值x̂k|k以及误差协方差值Pk|k,来预测k+1时刻的估计值,如式(11)所示:

其中协方差估计值Pk+1|k的系数 (1+2ΓMk+Γ2Jk)∈R1,则对于离散非线性系统改进的SRCKF算法,具体步骤如下:
1)初始化

其中chol(·)表示对矩阵进行乔利斯基分解。
2)时间更新
若k时刻系统后验状态估计量为,状态估计误差协方差平方根因子为Sk|k,过程噪声误差协方差矩阵Qk,观测噪声误差协方差矩阵Rk,观测向量yk,乘性噪声和观测噪声互协方差Gk,乘性噪声方差Uk,则一步状态预测值和协方差平方根因子为

对于n维状态变量,其容积点集,权重W(i)以及[1]i定义如下:

其中m=2n为容积点个数,表示对于三阶球面径向容积规则,采样容积点数为状态向量维度的两倍,[1]i表示第i个容积点向量,m在此又可表示为列向量的个数,每个容积点的向量维度与状态变量维度相同,κ(i)表示选取的m个容积采样点和分别表示先验状态向量估计值和先验误差协方差平方根估计矩阵,sqrt(·)为求平方根函数,qr(·)表示对矩阵进行QR分解,如式(15)所示Mk和Jk表示k时刻乘性噪声在观测序列条件下的乘性噪声均值和协方差。
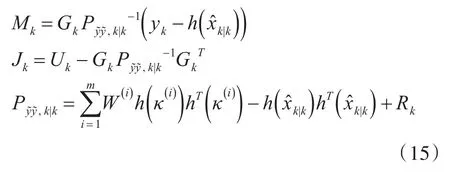
3)观测更新


其中ε(i)表示根据先验状态向量估计值和先验状态误差协方差平方根估计值产生观测方程的m个容积采样点(m=2n),δk+1|k(i)观测方程的非线性传播,和͂分别表示观测向量估计值和观测误差协方差平方根因子估计值表示状态向量和观测向量估计的误差互协方差值。

其中Kk+1为卡尔曼增益,和分别为后验状态向量估计值和后验误差协方差平方根因子估计值。
3 仿真分析
为了验证改进SRCKF滤波方法在乘性噪声条件下的性能,本仿真实验对比了EKF、SRCKF、SRUKF滤波方法,以均方根误差作为衡量标准,仿真实验添加了均方根值为1.8m的距离误差,1.8°的角度误差,0.9m/s的速度误差,且运动模型添加了均方根值为0.012的乘性噪声误差,且与观测噪声的互协方差为(0.025,0.0166,0.0125),实验过程中采用匀加速运动模型和雷达系统观测模型[14],雷达观测到的目标初始径向距离为20m,方位角为30°,速度为10m/s,运动模型分别在x和y方向上添加初始加速度为(2m/s,3.5m/s),目标运动方程f(·)和观测方程h(·)参照式(18)所示。


其中采样周期dt本例设置为0.02,如图1(a)和(b)所示采样点数为350个x,y方向上距离,速度,加速度的均方根误差曲线,图2(a)和(b)所示为x,y方向上距离维上15000次蒙特卡洛滤波实验均方根误差,可以看出改进SRCKF滤波算法均方根误差较其它滤波算法有更好的实验精度,统计结果如表1所示,基于乘性相关噪声的改进SRCKF滤波算法,在对复杂背景下受乘性相关噪声影响的系统,相较于传统的SRCKF算法在x方向上距离、速度、加速度的滤波精度分别提高了77.5%,41.0%,12.3%,y方向上则分别提高了77.6%,20.7%,54.8%,具有较好的滤波精度。

表1 EKF、SRCKF、SRUKF和改进SRCKF滤波算法均方根误差统计表
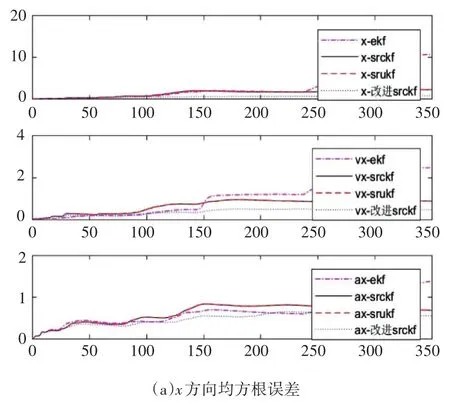

图1 x,y方向上均方根误差曲线图

图2 x,y方向上15000次蒙特卡洛均方根误差实验
4 结语
本文介绍了几种典型的非线性滤波算法,简单阐述其优缺点,并推导了在乘性相关噪声条件下的改进SRCKF滤波方法实现,最后通过仿真实验,对四种滤波算法的性能进行了对比分析,结果表明在随机的乘性相关噪声条件下,改进的SRCKF滤波精度更高,可应用于复杂环境下的目标跟踪。

