基于PBL教学模式的“曲线运动”教学设计
曹先辰 何林霞
(浙江省杭州市余杭第二高级中学,浙江 杭州 311100)
1 设计思路
PBL(problem-based learning)是以“问题引导,任务驱动”为抓手,学生主动思考、合作学习、完成学习任务的教学模式。PBL教学模式所蕴含的趣味性和实践性能够有效地促进学生核心素养的提升。[1]
“抛体运动”作为人教版必修二的第一章,拓展了学生对机械运动认识的广度,加深了学生对力与运动关系理解的深度。而“曲线运动”作为本章的第一节,是整章教学的基础。本节的主线就是通过观察与实验,让学生能够判定物体做曲线运动的方向,知道物体做曲线运动的条件。在此基础上通过进一步实验探索,让学生能够发现速度、合外力的方向与曲线运动弯曲情况之间的关系。
2 学习目标
2.1 物理观念
理解曲线运动的定义;会判断曲线运动的方向;知道曲线运动的运动性质;知道物体做曲线运动的条件;深化对平均速度和瞬时速度概念的认识。
2.2 科学思维
能够利用对比方法审视直线运动与曲线运动;理解并能运用极限法进行概念建构和知识应用。
2.3 科学探究
体验探究曲线运动速度方向的过程,通过理论分析验证实验结果的合理性;通过分组实验,感受自主实验、探究规律的过程,从而提升科学探究能力。
2.4 科学态度与责任
通过观察,感受物理与生活的紧密联系;通过实验,体会合作的意义,知道试错的价值以及科学规律的来之不易。
3 教学过程
3.1 回顾旧知,引出新课
播放女子铅球比赛的视频(图1),学生观察后,教师创设情境、提出问题。

图1
情境问题1:李梅素在1988年以21.76m创造了亚洲女子铅球纪录,这一纪录一直保持至今,请问21.76m是铅球离开手至落地时运动的位移大小吗?
自主任务1:学生在教师给出的图2上,大致画出铅球抛出至落地的运动轨迹,并在其上标注铅球的位移与运动员的成绩。

图2
师:同学们已经知道铅球的运动轨迹是曲线,并知道相应的位移大小。为什么铅球会做曲线运动?你能用在直线运动中学过的相关知识,准确描述曲线运动的位移、速度吗?
设计意图:PBL是一种教学模式,学生面对的是基于真实情景的问题,这些问题需要学生努力去寻找有意义的解决方案。教学中设计了学生熟悉的体育比赛作为课堂引入情景,充分利用学生已有的知识——位移,位移既是描述直线运动的重要物理量,也是描绘曲线运动不可或缺的,并基于此引出“主角”——曲线运动的速度。
3.2 描述曲线运动
自主任务2:小组交流,列举生活中常见的曲线运动。
教师利用课件展示图片、视频(图3至图6),学生观察认识生活中的曲线运动。

图3

图4

图5

图6
学生总结:物体运动轨迹是曲线的运动称为曲线运动。
情境问题2:现有一曲线运动如图7所示,已知该曲线运动的位移为l,经历的时间为t,请求出其平均速度。
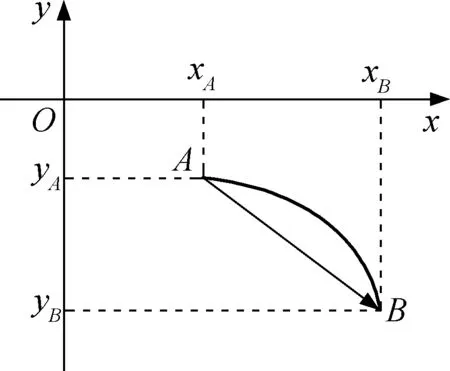
图7
设计意图:以生动直观的图片、视频等展示生活中的曲线运动,曲线运动的概念也跃然纸上。并由情景1中的位移概念引发关于坐标上“平均速度”的思考,自然带出重中之重“瞬时速度”。
情境问题2:图8所示的运动物体处于轨迹的C点时,瞬时速度朝什么方向呢?

图8
演示实验,学生观察:在平板底座上放置8块木板(图9),并从入口斜坡高处释放小球,观察小球的轨迹以及离开的位置(图10)。然后从右至左依次取走木板,分别观察小球离开曲线板后的运动情况。

图9

图10
学生交流:小球离开曲线板后做直线运动,且该直线与离开曲线板的位置相切,小球在离开曲线板的瞬间,速度方向沿该点的切线方向,我们可以提前预判小球运动会达到的位置。所以在问题2中,小球在C点的瞬时速度方向就是曲线C处的切线方向。
技术分享,提升思维:除了通过实验观察得到结论,另一种方式就是理论推导。利用现代教育GeoGebra软件,制作A到B的轨迹动图(图11),点击播放按钮就可以利用极限法探究曲线运动的瞬时速度方向。
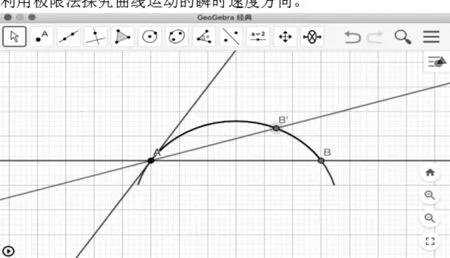
图11
设计意图:以生动直观的演示实验,学生会猜测出曲线运动瞬时速度的方向。实验观察、理论推导是学生认识物理规律的两条常见途径,紧接着过渡到GeoGebra软件,利用极限法探究瞬时速度方向。
自主任务3:图12中曲线AB是某物体的运动轨迹,请标出该过程平均速度的方向;B1、B2、B3、B4、B5是该物体在运动过程中经过的点,依次画出经过这些位置时平均速度的方向;从A到各个位置的平均速度,哪一个更接近A点的瞬时速度?若有一点B6(由于太接近A,图中未标出)比B5点还接近A,请判断这一极短时间内的平均速度方向。

图12
师生总结:质点在某一点的速度方向,沿曲线在这一点的切线方向。
设计意图:自主任务3让学生有机会通过作图体会平均速度和瞬时速度中Δt→0的意义,也为曲线运动的性质教学做了铺垫。
3.3 曲线运动的运动性质
情景问题3:如果保持速度大小不变,绕着学校操场跑一圈,可以认为这是匀速运动吗?那曲线运动属于怎样的运动呢?
生:运动过程中速度方向不断发生变化,不属于匀速运动,曲线运动是变速运动。
师生总结:由于做曲线运动的物体其运动状态发生变化,所以做曲线运动的物体受到的合外力一定不为0。
设计意图:知其然,知其所以然。自然引发学生思考:运动物体的速度方向为什么会发生改变?
3.4 探究物体做曲线运动的条件
自主任务4:教师提供一只乒乓球,请学生让该乒乓球做直线运动。
思考与操作:自由释放乒乓球,球在重力和空气阻力的共同作用下在竖直方向上做直线运动。
自主任务4:由静止释放乒乓球,在不允许接触乒乓球的条件下,能否让乒乓球做曲线运动?
思考与操作:对着下落的乒乓球吹气,通过操作发现难以成功。
实验支持:提供一台大功率吹风机,横向送风,释放小球并让其经过横风区。学生观察到小球的轨迹发生变化,发现乒乓球进入横风区之后做曲线运动。
提示:(1) 牛顿第一定律说明了力是改变物体运动状态的原因;(2) 曲线运动的速度大小变化虽未知,但速度方向一定变化,需要力来改变速度的方向;(3) 物体做匀变速直线运动,说明F与v同向,v变大,F与v反向,v变小;(4) 物体做曲线运动的条件是什么?
自主任务5:分组实验,寻找不同运动中速度方向与受力方向之间的关系。教师提供附着水写布的平板斜坡(图13),让沾过水的小球先从抬高的长边A释放。第一次静止释放,第二次给小球一个沿着长边的速度释放小球。观察小球两次运动在水写布上留下的轨迹,寻找两次运动中小球受到合力的方向,判断运动方向与受力方向之间的关系。

图13
教师补充:忽略摩擦力,视为光滑斜坡。
由于课堂时间有限,分组实验会出现学生做不出的情况,教师可以提前录好视频,供学生参考。
师生交流:当物体所受合外力的方向与它的速度方向不在同一直线上时,物体做曲线运动。
设计意图:运用PBL模式希望达到的结果是让学生体会到学习是一个循序渐进的开放式的过程,解决一个问题往往会带来新的问题,学习在动态进行。设计本组实验是想给学生创设两种运动情景:初速度为0、合外力恒定时物体的运动;初速度不为0且初速度方向与合外力方向垂直时物体的运动。但是,由于学生操作的规范性,比如运动平面前后有高低、初速度不沿长边等,能显示有规律的轨迹比较困难,所以有必要提前录好视频。针对学生动手操作中的一些实际问题也可以有意识地进行收集,成为之后的学习任务。
3.5 力的方向、速度方向与轨迹的关系
情境问题4:在曲线组合板实验中,如果抽走实验中的某片曲线板,小球还能做曲线运动吗?最多可以抽走几片?
对此问题部分学生颇感诧异,个别学生会给出正确答案。
操作与观察:依次抽走图9中8、6、3、1号板,小球均沿曲线运动。
提问与思考:该现象说明了什么问题?
交流与评估:物体做曲线运动所受合外力的方向总指向曲线的凹侧。
设计意图:从录制的视频中得出曲线运动的条件,再回到最初的演示实验,用已经得出的结论预测撤去曲线板小球的运动轨迹,并加以验证。
3.6 应用与巩固
情境问题5:呼应自主任务1,播放扔链球失败的视频。顺势提问:如图14所示,要使链球从保护网的开口A、B区域飞出获得成绩,运动员应当在圆周的哪个范围松手?
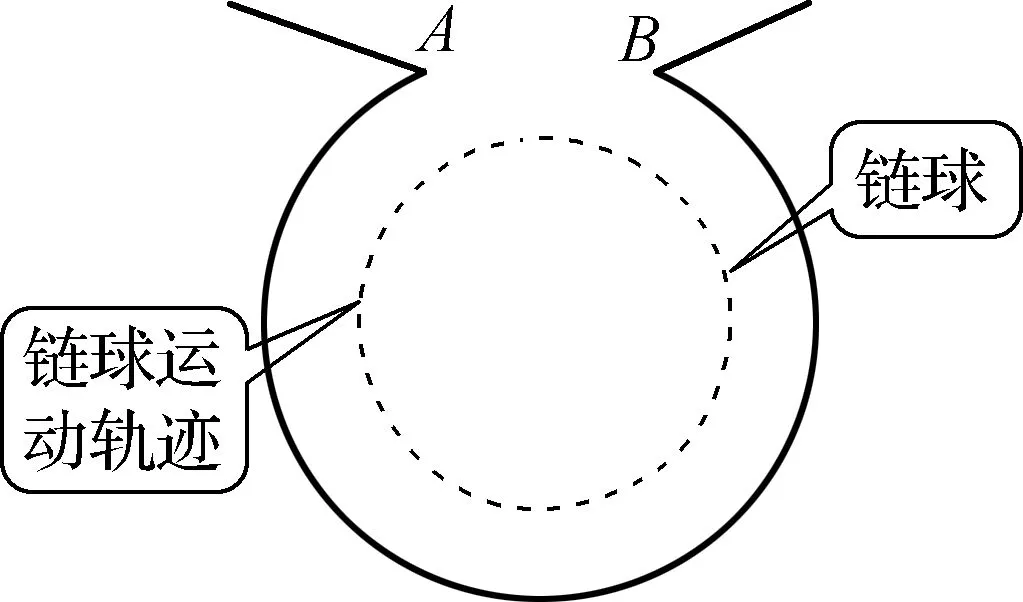
图14
思考与交流:在CD区域松手可以获得成绩(图15)。
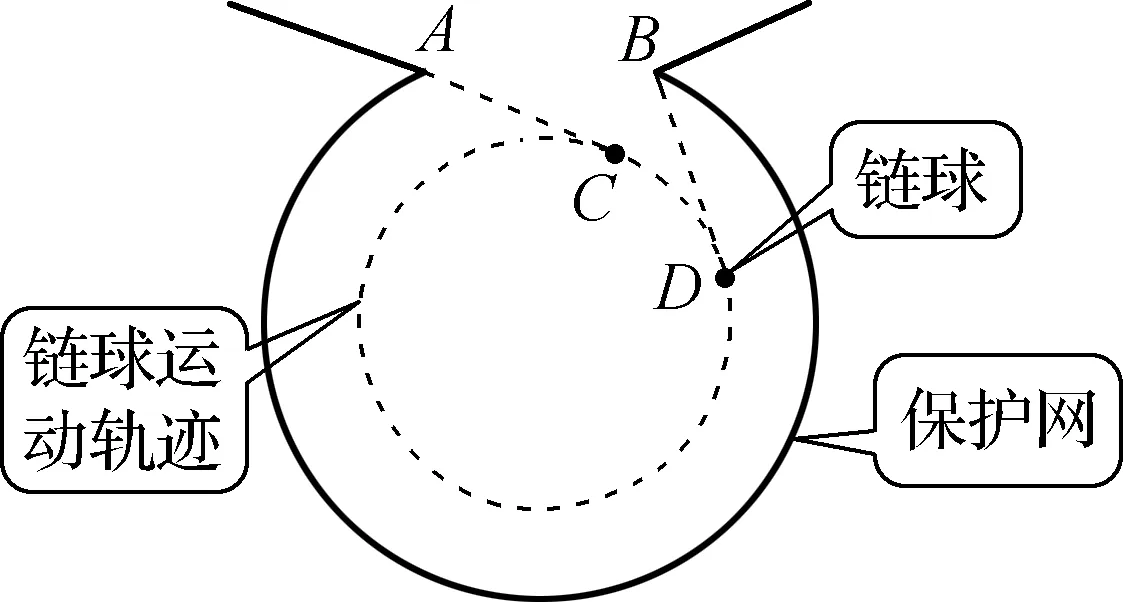
图15
自主任务6:呼应自主任务4,在图16中大致画出乒乓球由静止释放经过吹风机横风区下落至地面的轨迹(该情境中假设空气阻力保持不变,且小于重力,横风区风力恒定)。

图16
教师引导:对于区域1学生不存在问题,在区域2中乒乓球受到重力、阻力、风力的作用,在区域3中风力消失。教师在黑板上画出合力方向、初速度方向与轨迹关系图(图17)。
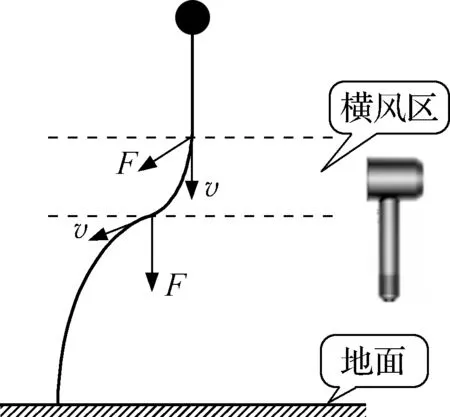
图17
设计意图:用已经得出的结论解释自主任务4中曲线运动实验成功和不成功的原因,且这个要求明显高于前一个任务,要求画出各个位置的速度、受力方向。由此,整节课的知识重点在最后这个自主任务中得以应用,考查了学生本节课的学习成果。
4 教学反思
在PBL中,教师和学生的关系就像硬币的两面,一方的活动以另一方为前提,两者不可分开。师生交互建立在平等的基础上,教师对于学生来说更多的是作为一种资源存在,同样地,学生对于教师来说也是一种资源,在平等的对话、交流中实现教学相长。[3]“曲线运动”的教学以真实情景问题为引导,以学生自主任务为驱动,尊重教师主导下的学生主体地位,学生合作探究、积极思考,课堂是丰满且有趣的。最初PBL模式并不重视问题的严谨性,甚至主动设计劣构性问题,让学生不仅拥有解决问题的能力,还具有批判性的思维能力。但45分钟的课堂时间有限,改为良构性问题不仅有利于课堂进度的把握,也有利于学生应试能力的提升。
本节教学设计内容丰富,且未降低思维的难度,对于层次较低的学生群体而言,课堂进度推进可能存在难以预计的状况,教师也要有所取舍。一些设计的环节可以根据学情删减,一些任务也可以在课后完成。
无论具体实施哪些步骤,要以核心素养为导向,以新课程基本理念为指导,精细化设计教学目标和过程,始终把学生主动学习放在首位,通过学生合作,主动探究,促进学生的发展。

